中考数学模拟试题命题双向细目表及模拟卷 12页

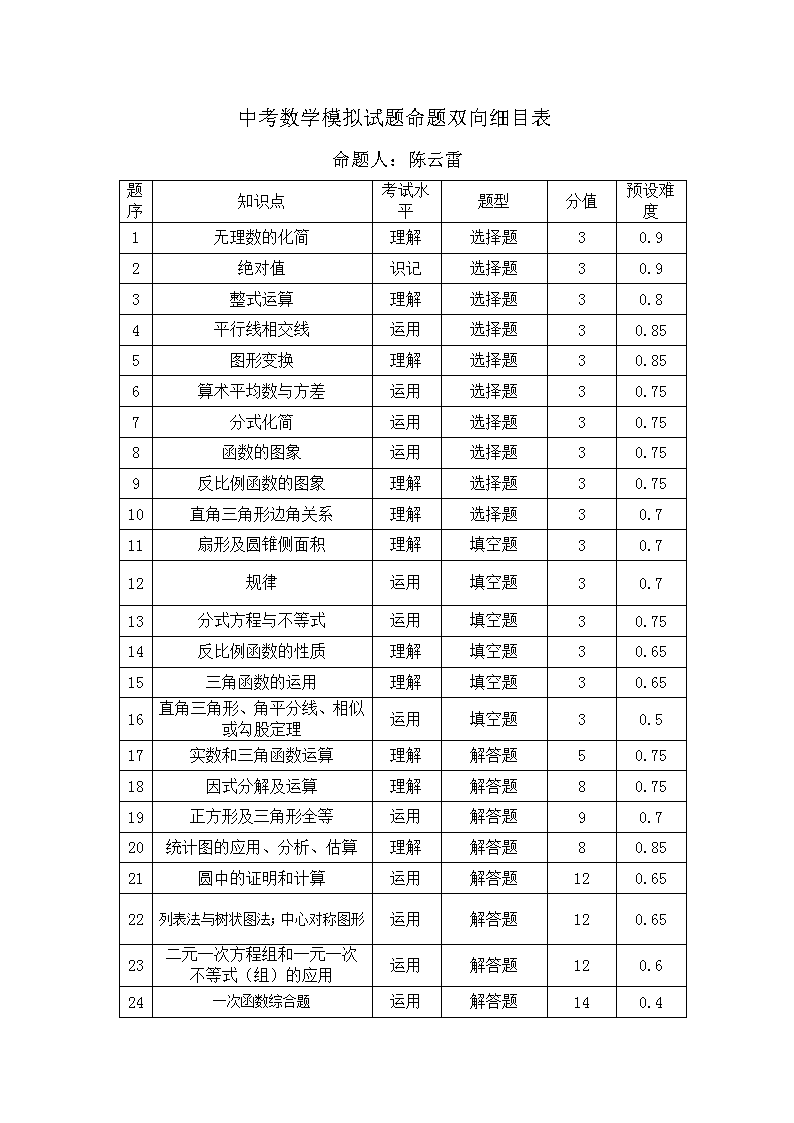
中考数学模拟试题命题双向细目表 命题人：陈云雷 题序 知识点 考试水平 题型 分值 预设难度 ‎1‎ 无理数的化简 理解 选择题 ‎3‎ ‎0.9‎ ‎2‎ 绝对值 识记 选择题 ‎3‎ ‎0.9‎ ‎3‎ 整式运算 理解 选择题 ‎3‎ ‎0.8‎ ‎4‎ 平行线相交线 运用 选择题 ‎3‎ ‎0.85‎ ‎5‎ 图形变换 理解 选择题 ‎3‎ ‎0.85‎ ‎6‎ 算术平均数与方差 运用 选择题 ‎3‎ ‎0.75‎ ‎7‎ 分式化简 运用 选择题 ‎3‎ ‎0.75‎ ‎8‎ 函数的图象 运用 选择题 ‎3‎ ‎0.75‎ ‎9‎ 反比例函数的图象 理解 选择题 ‎3‎ ‎0.75‎ ‎10‎ 直角三角形边角关系 理解 选择题 ‎3‎ ‎0.7‎ ‎11‎ 扇形及圆锥侧面积 理解 填空题 ‎3‎ ‎0.7‎ ‎12‎ 规律 运用 填空题 ‎3‎ ‎0.7‎ ‎13‎ 分式方程与不等式 运用 填空题 ‎3‎ ‎0.75‎ ‎14‎ 反比例函数的性质 理解 填空题 ‎3‎ ‎0.65‎ ‎15‎ 三角函数的运用 理解 填空题 ‎3‎ ‎0.65‎ ‎16‎ 直角三角形、角平分线、相似或勾股定理 运用 填空题 ‎3‎ ‎0.5‎ ‎17‎ 实数和三角函数运算 理解 解答题 ‎5‎ ‎0.75‎ ‎18‎ 因式分解及运算 理解 解答题 ‎8‎ ‎0.75‎ ‎19‎ 正方形及三角形全等 运用 解答题 ‎9‎ ‎0.7‎ ‎20‎ 统计图的应用、分析、估算 理解 解答题 ‎8‎ ‎0.85‎ ‎21‎ 圆中的证明和计算 运用 解答题 ‎12‎ ‎0.65‎ ‎22‎ 列表法与树状图法；中心对称图形 运用 解答题 ‎12‎ ‎0.65‎ ‎23‎ 二元一次方程组和一元一次不等式（组）的应用 运用 解答题 ‎12‎ ‎0.6‎ ‎24‎ 一次函数综合题 运用 解答题 ‎14‎ ‎0.4‎ 命题说明 1、 在数与式、几何图形、函数及图象、概率与统计等方面力求都有突出重点，并能做到覆盖面广，避免知识点重复。‎ 2、 结合考纲考点，着重考查基础知识原理，重视知识点原理简单的迁移，不出偏繁和太难的题目。‎ 3、 在不同题型的最后一题设置迁移性较大的题目，以考查学生的灵活性和熟练程度。‎ 4、 第21、22、23题中坡度设置问题，从基础开始进行拓展，保证学生的得分率。‎ 中考数学模拟试题 说明：1、全卷分二部分，第一部分为选择题，第二部分为非选择题，共6页。考试时间120分钟，满分150分。‎ ‎2、本卷试题，考生必须在答题卡上按规定作答；凡在试卷、草稿纸上作答的，其答案一律无效。答题卡必须保持清洁，不能折叠。‎ ‎3、本卷选择题1—10，每小题选出答案后，用2B铅笔将答题卡选择题答题区内对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案；非选择题11—24，答案（含作辅助线）必须用规定的笔，按作答题目序号，写在答题卡非选择题答题区内。‎ 第一部分 选择题 ‎（本部分共10小题，每小题4分，共40分。每小题给出4个选项，其中只有一个是正确的）‎ ‎1、化简的结果是 (　 　) ‎ A.2　　　　　B. C. D.‎ ‎2、如果与1互为相反数，则等于（ ）‎ A．2 B． C．1 D．‎ ‎3、下列运算正确的是　　　　　　　　　　　　　　　　　　　　　（　　 ）　‎ ‎ A.　 B. X|k | B| 1 . c|O |m ‎ C. D.‎ ‎4、如图所示，AB∥CD，∠E＝37°，∠C＝20°，则∠EAB的度数为（　　）‎ ‎（第5题）‎ A.57° B.60° C.63° D.123 ‎ ‎（第4题）‎ ‎5、在下列四种图形变换中，本题图案不包含的变换是（ ）‎ A．位似　B．旋转　C．轴对称　 D．平移 ‎ 6、 数据3、1、x、－1、－3的平均数是0，则这组数据的方差是　（　　）‎ ‎　　　A.1 B.2 C.3 D.4 全 ‎7、化简的结果是（ ）‎ A． B． C． D．‎ ‎8、如图，三个大小相同的正方形拼成六边形，一动点从点出发沿着→→→→ 方向匀速运动，最后到达点.运动过程中的面积（）随时间（t）变化的图象大致是（ ）‎ A．。‎ B D C ‎（第6题）‎ ‎.‎ ‎.‎ ‎.‎ ‎·‎ ‎9、反比例函数的图象经过点，则该反比例函数图象在（ ）‎ A．第一、三象限 B．第二、四象限 ‎ C．第二、三象限 D．第一、二象限 ‎10、如图已知一商场自动扶梯的长L为‎10米，该自动扶梯到达的高度h为‎6米，自动扶梯与地面所成的角为θ，则tanθ的值等于 （ ）‎ ‎ A、 B、 C、 D、‎ θ h L ‎ ‎ ‎(第10题) （第11题）‎ 第二部分 非选择题 填空题（本题共6小题，每小题5分，共30分）‎ ‎11、． 如图1已知扇形的半径为‎6cm，圆心角的度数为，若将此扇形围成一个圆锥，则围成的圆锥的侧面积为 　　 X|k | B| 1 . c|O |m ‎12、如图，填在四个田字格内的数有相同的规律，根据此规律，则C所表示的数值为 ▲ .‎ ‎1‎ ‎3‎ ‎5‎ ‎8‎ ‎3‎ ‎5‎ ‎7‎ ‎22‎ ‎5‎ ‎7‎ ‎9‎ ‎44‎ ‎7‎ A B C ‎13、关于x的方程的解是负数，则m的取值范围是 _▲ 　　．‎ ‎14、若点A(–2，a)、B(–1，b)、C(1，c)都在反比例函数y=(k<0)的图象上，则用“<”连接a、b、c的大小关系为________▲___________．‎ ‎15、如图，某渔船在海面上朝正东方向匀速航行，在A处观测到灯塔M在北偏东60º方向上，航行半小时后到达B处，此时观测到灯塔M在北偏东30º方向上，那么该船继续航行____▲________分钟可使渔船到达离灯塔距离最近的位置．‎ C A D B E A B M 北 北 ‎30º ‎ ‎60º ‎ 东 ‎（第15题图） （第16题图）‎ ‎16、如图，在Rt△ABC中，∠C＝90°，AC＝4，BC＝3，BD平分∠ABC，‎ E是AB中点，连接DE，则DE的长为． 　　．‎ 三、解答题 ‎17．（本题满分 5 分）计算：．‎ ‎18．（本题满分8分）已知：，，求下列各式的值.‎ ‎（1）；（3分） （2）．（3分）‎ ‎19．（本小题满分9分）‎ 如图 ，ABCD是正方形．G是 BC 上的一点，DE⊥AG于 E，BF⊥AG于 F． ‎ A D E F C G B ‎（1）求证：；（4分） ‎ ‎（2）求证：．（5分）‎ 新- 课 -标-第 -一- 网 ‎20．(本题满分8分)某校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查，得到一组学生捐款情况的数据，下图是根据这组数据绘制的统计图，图中从左到右各长方形高度之比为3∶4∶5∶8∶2，又知此次调查中捐15元和20元的人数共39人．‎ ‎(1)他们一共抽查了多少人？捐款数不少于20元的概率是多少？‎ ‎(2)这组数据的众数、中位数各是多少？‎ ‎(3)若该校共有2310名学生，请估算全校学生共捐款多少元？‎ 第20题图 ‎21． (本题满分12分)‎ 如图，两个同心圆的圆心是O，大圆的半径为13，小圆的半径为5，AD是大圆的直径．大圆的弦AB，BE分别与小圆相切于点C，F．AD，BE相交于点G，连接BD．‎ A C B D G F E O ‎(第21题)‎ ‎(1)求BD 的长；‎ ‎(2)求∠ABE+2∠D的度数；‎ ‎(3)求的值．‎ http://w ww.xk b1. co ‎ ‎22.（12分）有四张背面相同的纸牌A，B，C，D，其正面分别划有四个不同的稽核图形（如图）．小华将这4张纸牌背面朝上洗匀后摸出一张，放回洗匀后再摸出一张．‎ ‎（1）用树状图（或列表法）表示两次模牌所有可能出现的结果（纸牌可用A、B、C、D表示）；‎ ‎（2）求摸出两张牌面图形都是中心对称图形的纸牌的概率．‎ ‎23．（本小题满分12分）‎ 为实现区域教育均衡发展，我市计划对某县、两类薄弱学校全部进行改造．根据预算，共需资金1575万元．改造一所类学校和两所类学校共需资金230万元；改造两所类学校和一所类学校共需资金205万元．‎ ‎ （1）改造一所类学校和一所类学校所需的资金分别是多少万元？‎ ‎ （2）若该县的类学校不超过5所，则类学校至少有多少所？‎ ‎ （3）我市计划今年对该县、两类学校共6所进行改造，改造资金由国家财政和地方财政共同承担．若今年国家财政拨付的改造资金不超过400万元；地方财政投入的改造资金不少于70万元，其中地方财政投入到、两类学校的改造资金分别为每所10万元和15万元．请你通过计算求出有几种改造方案？‎ ‎24．（14分）如图①，矩形ABCD被对角线AC分为两个直角三角形，AB=3，BC=6．现将Rt△ADC绕点C顺时针旋转90°，点A旋转后的位置为点E，点D旋转后的位置为点F．以C为原点，以BC所在直线为x轴，以过点C垂直于BC的直线为y轴，建立如图②的平面直角坐标系．http://w ww.xk b1. co ‎ ‎（1）求直线AE的解析式；‎ ‎（2）将Rt△EFC沿x轴的负半轴平行移动，如图③．设OC=x（0＜x≤9），Rt△EFC与Rt△ABO的重叠部分面积为s；求当x=1与x=8时，s的值；‎ ‎（3）在（2）的条件下s是否存在最大值？若存在，求出这个最大值及此时x的值；若不存在，请说明理由．‎ 中考数学模拟试题 参考答案及评分意见 第一部分 选择题（本部分共10小题，每小题3分，共30分）‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ B C C A D D D B B A 第二部分 填空题（本题共6小题，每小题3分，共18分）‎ ‎11‎ ‎12‎ ‎13‎ ‎14‎ ‎15‎ ‎16‎ m﹤2且m≠0‎ ‎74‎ M《2‎ c