赤峰中考数学试题 11页

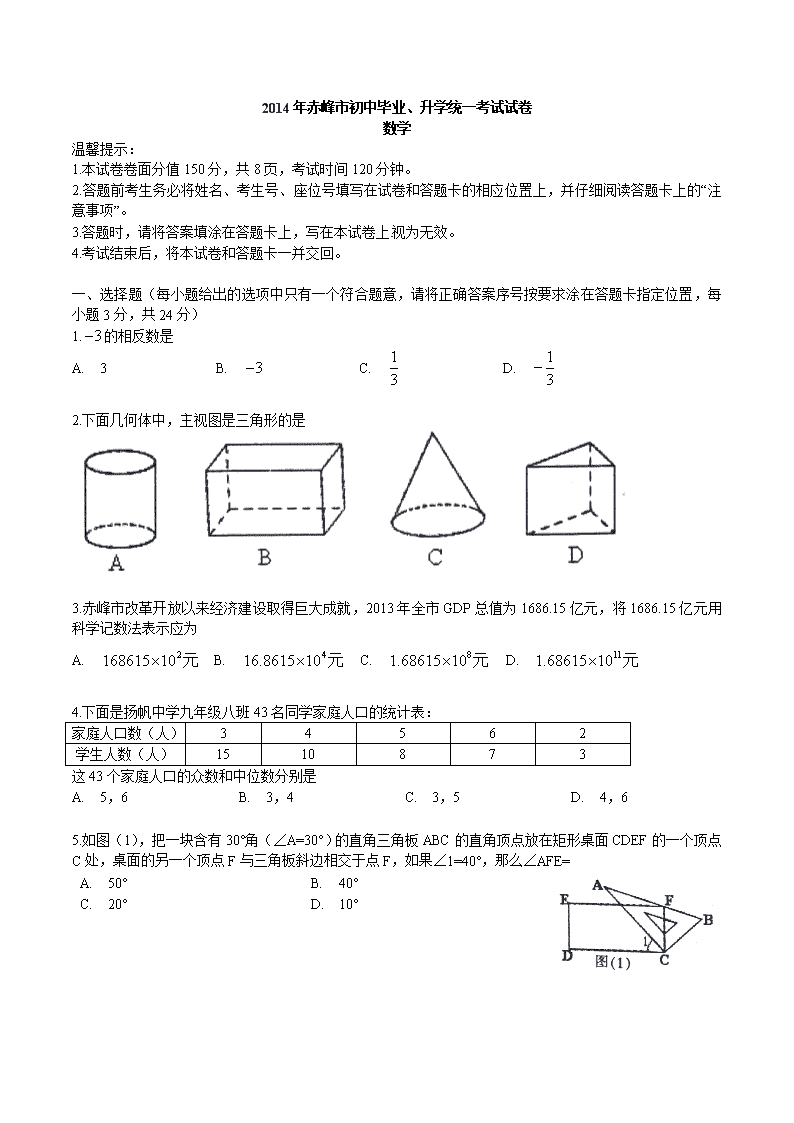
‎2014年赤峰市初中毕业、升学统一考试试卷 数学 温馨提示：‎ ‎1.本试卷卷面分值150分，共8页，考试时间120分钟。‎ ‎2.答题前考生务必将姓名、考生号、座位号填写在试卷和答题卡的相应位置上，并仔细阅读答题卡上的“注意事项”。‎ ‎3.答题时，请将答案填涂在答题卡上，写在本试卷上视为无效。‎ ‎4.考试结束后，将本试卷和答题卡一并交回。‎ 一、选择题（每小题给出的选项中只有一个符合题意，请将正确答案序号按要求涂在答题卡指定位置，每小题3分，共24分）‎ ‎1.的相反数是 A.‎ ‎3‎ B.‎ C.‎ ‎ ‎ D.‎ ‎2.下面几何体中，主视图是三角形的是 ‎3.赤峰市改革开放以来经济建设取得巨大成就，2013年全市GDP总值为1686.15亿元，将1686.15亿元用科学记数法表示应为 A.‎ B.‎ C.‎ D.‎ ‎4.下面是扬帆中学九年级八班43名同学家庭人口的统计表：‎ 家庭人口数（人）‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎2‎ 学生人数（人）‎ ‎15‎ ‎10‎ ‎8‎ ‎7‎ ‎3‎ 这43个家庭人口的众数和中位数分别是 A.‎ ‎5，6‎ B.‎ ‎3，4‎ C.‎ ‎3，5‎ D.‎ ‎4，6‎ ‎5.如图（1），把一块含有30°角（∠A=30°）的直角三角板ABC的直角顶点放在矩形桌面CDEF的一个顶点C处，桌面的另一个顶点F与三角板斜边相交于点F，如果∠1=40°，那么∠AFE=‎ A.‎ ‎50°‎ B.‎ ‎40°‎ C.‎ ‎20°‎ D.‎ ‎10°‎ ‎6.如图（2），AB是⊙O的直径，C、D是⊙O上两点，CD⊥AB，若∠DAB=65°，则∠BOC=‎ A.‎ ‎25°‎ B.‎ ‎50°‎ C.‎ ‎130°‎ D.‎ ‎155°‎ ‎7.化简结果正确的是 A.‎ ‎ ‎ B.‎ C.‎ ‎ ‎ D.‎ ‎ ‎ ‎8.如图（3），一根长为5米的竹竿AB斜立于墙AC的右侧，底端B与墙角C的距离为3米，当竹竿顶端A下滑米时，底端B便随着向右滑行米，反映与变化关系的大致图象是 二、填空题（请把答案填写在答题卡相应的横线上，每小题3分，共24分）‎ ‎9.化简：‎ ‎10.一只蚂蚁在图（4）所示的矩形地砖上爬行，蚂蚁停在阴影部分的概率为多少？‎ ‎11.下列四个汽车图标中，既是中心对称图形又是轴对称图形的图标有几个？‎ ‎12.如图（5），E是矩形ABCD中BC边的中点，将△ABE沿AE折叠到△AEF，F在矩形ABCD内部，延长AF交DC于G点，若∠AEB=550, ‎ ‎∠DAF的度数？‎ ‎13.如图（6），反比例函数的图象与以原点为圆心的圆交于A、B两点，且，求图中阴影部分的面积？（结果保留）。‎ ‎14.如图（7）所示，在象棋盘上建立平面直角坐标系，使“马”位于点（2，2），“炮”位于点（-1，2），写出“兵”所在位置的坐标。‎ ‎15.直线过点，该直线的解析式可以写为？（只写出一个即可）‎ ‎16.平移小菱形◇可以得到美丽的“中国结”图案，下面四个图案是由◇平移后得到的类似“中国结”的图案，按图中规律，第20个图案中，小菱形的个数是多少？‎ 三、解答题（在答题卡上解答，答在本试卷上无效，解答时要写出必要的文字说明、证明过程或演算步骤，共10题，满分102分）‎ ‎17.（6分）计算：‎ ‎18.（6分）求不等式组 的正整数解.‎ ‎19.（10分）如图（8），已知△ABC中AB=AC ‎（1）作图：在AC上有一点D，延长BD，并在BD的延长线上取点E，使AE=AB，连AE，作∠EAC的平分线AF，AF交DE于点F（用尺规作图，保留作图痕迹，不写作法）；‎ ‎（2）在（1）条件下，连接CF，求证：∠E=∠ACF ‎20.（10分）自从中央公布“八项规定”以来，光明中学积极开展“厉行节约，反对浪费”活动.为此，学校学生会对九年级八班某日午饭浪费饭菜情况进行调查，调查内容分为四种：A.饭和菜全部吃光；B.有剩饭但菜吃光；C.饭吃光但菜有剩；D.饭和菜都有剩.学生会根据统计结果，绘制如下两个统计图，根据统计图提供的信息回答下列问题：‎ ‎（1）九年级八班共有多少学生？‎ ‎（2）计算图（10）中B所在扇形的圆心角的度数，并补全条形统计图；‎ ‎（3）光明中学有学生2000名，请估计这顿午饭有剩饭的学生人数，按每人平均10克米饭计算，这顿午饭将浪费多少千克米饭？‎ ‎21.（10分）位于赤峰市宁城的“大明塔”是我国辽代的佛塔，距今已有1千多年的历史.如图（11），王强同学为测量大明塔的高度，在地面的点E处测得塔基BC上端C的仰角为30°，他又沿BE方向走了26米，到达点F处，测得塔顶端A的仰角为52°，已知塔基是以OB为半径的圆内接正八边形，B点在正八边形的一个顶点上，塔基半径OB=18米，塔基高BC=11米，求大明塔的高OA（结果保留到整数， ）‎ ‎22.（10分）某养殖专业户计划购买甲、乙两种牲畜.已知乙种牲畜的单价是甲种牲畜单价的2倍多200元，买3头甲种牲畜和1头乙种牲畜共需5700元.‎ ‎（1）甲、乙两种牲畜的单价各是多少元？‎ ‎（2）若购买以上两种牲畜50头，共需资金9.4万元，求甲、乙两种牲畜各购买多少头？‎ ‎（3）相关资料表明：甲、乙两种牲畜的成活率分别为95%和99%，若使这50头牲畜的成活率不低于97%且购买的总费用最低，应如何购买？‎ ‎23.（12分）如图（12），矩形OABC的顶点A、C分别在轴和轴上，点B的坐标为，双曲线的图象经过BC的中点D，且于AB交于点E.‎ ‎（1）求反比例函数解析式和E点坐标；‎ ‎（2）若F是OC上一点，且以∠OAF和∠CFD为对应角的△FDC和△AFO相似，求F点的坐标.‎ ‎24.（12分）如图（13），E是直线AB、CD内部一点，AB∥CD，连接EA、ED ‎（1）探究猜想：‎ ‎①若∠A=30°，∠D=40°，则∠AED等于多少度？‎ ‎②若∠A=20°，∠D=60°，则∠AED等于多少度？‎ ‎③猜想图（13）中∠AED、∠EAB、∠EDC的关系并证明你的结论.‎ ‎（2）拓展应用：‎ 如图（14），射线FE与矩形ABCD的边AB交于点E，与边CD交于点F，①②③④分别是被射线FE隔开的4个区域（不含边界，其中区域③④位于直线AB上方），P是位于以上四个区域上点，猜想：∠PEB、∠PFC、∠EPF的关系（不要求证明）.‎ ‎25.（12分）阅读下面材料：‎ 如图（15），圆的概念：在平面内，线段PA绕它固定的一个端点P旋转一周，另一个端点A所形成的图形叫做圆.‎ 就是说，到某个定点等于定长的所有点在同一个圆上.‎ 圆心在，半径为的圆的方程可以写为：.‎ 如：圆心在，半径为5的圆的方程为：.‎ ‎（1）填空：‎ ‎①以为圆心， 1为半径的圆的方程为： ；‎ ‎②以为圆心， 为半径的圆的方程为： ；‎ ‎（2）根据以上材料解决以下问题：‎ 如图（16），以为圆心的圆与轴相切于原点，C是⊙B上一点，连接OC，作BD⊥OC垂足为D，延长BD交轴于点E，已知.‎ ‎①连接EC，证明EC是⊙B的切线；‎ ‎②在BE上是否存在一点P，使PB=PC=PE=PO，若存在，求P点坐标，并写出以P为圆心，以PB为半径的⊙P的方程；若不存在，说明理由.‎ ‎26.（14分）如图（17），抛物线与轴交于点，两点，与轴交于点.‎ ‎（1）求该抛物线的解析式及顶点M的坐标；‎ ‎（2）求△BCM面积与△ABC面积的比；‎ ‎（3）若P是轴上一个动点，过P作射线PQ∥AC交抛物线于点Q，随着P点的运动，在抛物线上是否存在这样的点Q，使以A、P、Q、C为顶点的四边形为平行四边形？若存在请求出Q点的坐标；若不存在，请说明理由.‎ ‎2014年赤峰市初中毕业、升学统一考试试卷 数学 参考答案及评分标准 一、选择题（每小题3分，共24分）‎ ‎1.A ‎2.C ‎3.D ‎4.B ‎5.D ‎6.C ‎7.B ‎8.A 二、填空题（每小题3分，共24分）‎ ‎9.‎ ‎10. ‎ ‎11.1个 ‎12.20°‎ ‎13. ‎ ‎14. ‎ ‎ (不唯一，写对即可）‎ ‎16.800个 三、解答题（如有不同于本答案的正确答案，请参照本答案赋分标准给分）‎ ‎17.解：原式= ………………（3分）‎ ‎ = ……………………………………（6分）‎ 评分阈值：1分 ‎18.解：由（1）得 ∴ ……………………（2分）‎ ‎ 由（2）得 ∴ ……………………（4分）‎ ‎∴不等式组的解集为 ……………………（5分）‎ 评分阈值：1分 ‎19.解：（1）作图正确（5分）‎ ‎ （2）证明：在△ACF和△AEF中 ‎∵AE=AB=AC ………………（6分）‎ ‎ ∠EAF=∠CAF ………………（7分）‎ ‎ AF=AF ………………（8分）‎ ‎∴△ACF≌△AEF ………………（9分）‎ ‎∴∠E=∠ACF ………………（10分）‎ 评分阈值：1分 ‎20.解：（1）30÷60%=50（人） …………（2分）‎ ‎（2）有剩饭菜吃光的人数为50-30-5-5=10（人） ……（3分）‎ 图作正确 …………（4分）‎ 圆心角为： …………（6分）‎ ‎（3）有剩饭的人数为（人）…………（8分）‎ ‎600×10=6（千克） ………………（10分）‎ 评分阈值：1分 ‎21.在Rt△CBE中，∠CEB=30°，BC=11‎ ‎∴EC=22 ………………（2分）‎ 由勾股定理 …………（4分）‎ 在Rt△AOF中，∠AFO=52°，‎ OF=18+19+26=63 且 …………（6分）‎ ‎∴OA= …………（8分）‎ ‎ =63×1.28‎ ‎ ≈81（米）………………（10分）‎ 评分阈值：1分 ‎22.解：（1）设甲种牲畜的单价是元 依题意：3+2+200=5700 …………（1分）‎ 解得：=1100 2+200=2400 ………………（2分）‎ 即甲种牲畜的单价是1100元，乙种牲畜的单价是2400元 …………（3分）‎ ‎（2）设购买甲种牲畜头 依题意：1100+2400(50-)=94000 …………（4分）‎ 解得：=20 (50-)=30 ………………（5分）‎ 即甲种牲畜购买20头，乙种牲畜购买30头 …………（6分）‎ ‎（3）设费用为购买甲种牲畜头 则=1100+240(50-) ………………（7分）‎ ‎ =-1300+120000‎ 依题意： …………（8分）‎ 解得： ‎ ‎∵=-1300<0 ∴随增大而减小………………（9分）‎ ‎∴当=25时费用最低，所以各购买25头时满足条件………………（10分）‎ 评分阈值：1分 ‎23.解：（1）四边形ABCD是矩形，D是BC中点， ‎ ‎∴ …………（1分）‎ 设反比例函数解析式为 …………（2分）‎ ‎∵ ∴ …………（3分）‎ 当时，………………（4分）‎ ‎∴ ……………………（5分）‎ ‎（2）设 ‎ ‎∵∠OAF=∠DFC △AOF∽△FDC ‎∴ 即 …………（8分）‎ ‎∴ …………（10分）‎ 解得： …………（11分）‎ ‎∴或 ……………………（12分）‎ 评分阈值：1分 ‎24.解：（1）①∠AED=70° ②∠AED=80° ③∠AED=∠EAB+∠EDC…………（4分）‎ 证明：延长AE交DC于点F ‎∵AB∥DC ‎∴∠EAB=∠EFD…………………………………………(5分)‎ 又∵∠AED是△EFD的外角 ‎∴∠AED=∠EDF+∠EFD…………………………………(7分)‎ ‎ =∠EAB+∠EDC…………………………………(8分)‎ ‎(2)P点在区域①时：‎ ‎∠EPF=3600 -(∠PEB+∠PFC) …………………………(9分)‎ P点在区域②时：‎ ‎∠EPF=∠PEB+∠PFC………………………………… (10分)‎ P点在区域③时：‎ ‎∠EPF=∠PEB-∠PFC………………………………… (11分)‎ P点在区域④时：‎ ‎∠EPF=∠PFC-∠PFB………………………………… (12分)‎ 评分阈值：1分 ‎25.解：（1）①方程为：……………………… (2分)‎ ‎ ②方程为：………………(4分)‎ ‎ （2）①证明 ‎ ∵OB=BC BD⊥OC ‎ ∴∠OBD=∠CBD ‎∵BE=BE ‎ ‎∴△BOE≌△BCE……………………………………(6分)‎ ‎∵AO⊥OE ‎∴∠BCE=∠BOE=900‎ ‎∴EC是⊙B的切线…………………………………(7分)‎ ‎②存在 取BE的中点P连接PC、PO……………………… (8分)‎ ‎∵△BCE和△BOE是直角三角形 ‎∴PC=BE PO=BE……………………… (9分)‎ ‎∴PC=PB=PO=PE 过P作PM⊥轴于M、PN⊥轴于N ‎∵P是BE中点 ‎∴OM=OB ON=OE ‎∵∠AOC+∠EOC=900 ∠BEO+∠EOC=900 ‎ ‎∴∠AOC=∠BEO ………………（10分）‎ ‎∴ ∴‎ ‎ ，即 ∴BE=10‎ 由勾股定理： ‎ ‎ ， …………………………（11分）‎ ‎∴⊙P的方程为 …………………………（12分）‎ 评分阈值：1分 ‎26.解：（1）设抛物线解析式为 ‎ ‎∵抛物线过点 ‎ ‎∴ ………………（2分）‎ ‎∴ ‎ 抛物线解析式为………（4分）‎ ‎∵ ∴‎ ‎（2）连BC、BM、CM，作MD⊥轴于D…………（6分）‎ ‎∵‎ ‎ =‎ ‎ = ………………（7分）‎ ‎ ………………（8分）‎ ‎ ………………（9分）‎ ‎（3）存在………………（10分）‎ ‎①当Q点在轴下方时，作QE⊥轴于E ‎∵AC∥PQ且AC=PQ ∴OC=EQ=3‎ ‎ 解得：（舍） ∴ …………（11分）‎ ‎②当Q点在轴上方时，作QF⊥轴于F ‎∵AC∥PQ且AC=PQ ∴Rt△OAC≌Rt△FPQ ∴OC=FQ=3‎ ‎ 解得： ‎ ‎∴ 或…………（13分）‎ 综上，满足条件的Q点为或或…………（14分）‎ 评分阈值：2分