2018中考数学专题训练圆含解析 21页

专题训练 ‎ (圆)‎ ‎(120分钟　120分)‎ 一、选择题(本大题共20小题,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来,每小题选对得3分,选错、不选或选出的答案超过一个,均记零分)‎ ‎1.半径为5的圆的一条弦长不可能是　(　　)‎ A.3　　　 　B‎.5　‎　　 　C.10　　　 　D.12‎ ‎【解析】选D.因为圆中最长的弦为直径,所以弦长l≤10.‎ ‎2.有下列四个说法:①半径确定了,圆就确定了;②直径是弦;③弦是直径;④半圆是弧,但弧不一定是半圆.‎ 其中错误说法的个数是　(　　)‎ A.1 B‎.2 ‎ C.3 D.4‎ ‎【解析】选B.①圆确定的条件是确定圆心与半径,①是假命题,故此说法错误;‎ ‎②直径是弦,直径是圆内最长的弦,是真命题,故此说法正确;‎ ‎③弦是直径,只有过圆心的弦才是直径,是假命题,故此说法错误;‎ ‎④半圆是弧,但弧不一定是半圆,圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫半圆,所以半圆是弧.但比半圆大的弧是优弧,比半圆小的弧是劣弧,所以不是所有的弧都是半圆,是真命题,故此说法正确.其中错误的说法是①③.‎ ‎3.(2017·兰州中考)如图,在☉O中,=,点D在☉O上,∠CDB=25°,则∠AOB=　‎ ‎(　　)‎ A.45° B.50° C.55° D.60°‎ ‎【解析】选B.因为在☉O中,=,点D在☉O上,∠CDB=25°,所以∠AOB=‎ ‎2∠CDB=50°.‎ ‎4.(2016·无锡中考)如图,AB是☉O的直径,AC切☉O于A,BC交☉O于点D,若 ‎∠C=70°,则∠AOD的度数为　(　　)‎ A.70° B.35° C.20° D.40°‎ ‎【解析】选D.∵AC是圆O的切线,AB是圆O的直径,‎ ‎∴AB⊥AC.∴∠CAB=90°.‎ 又∵∠C=70°,∴∠CBA=20°.∴∠AOD=40°.‎ ‎5.(2017·自贡中考)AB是☉O的直径,PA切☉O于点A,PO交☉O于点C;连接BC,若∠P=40°,则∠B等于　(　　)‎ A.20° B.25° C.30° D.40°‎ ‎【解析】选B.因为PA切☉O于点A,所以∠PAB=90°,因为∠P=40°,所以 ‎∠POA=90°-40°=50°,因为OC=OB,所以∠CBO=∠BCO=25°.‎ ‎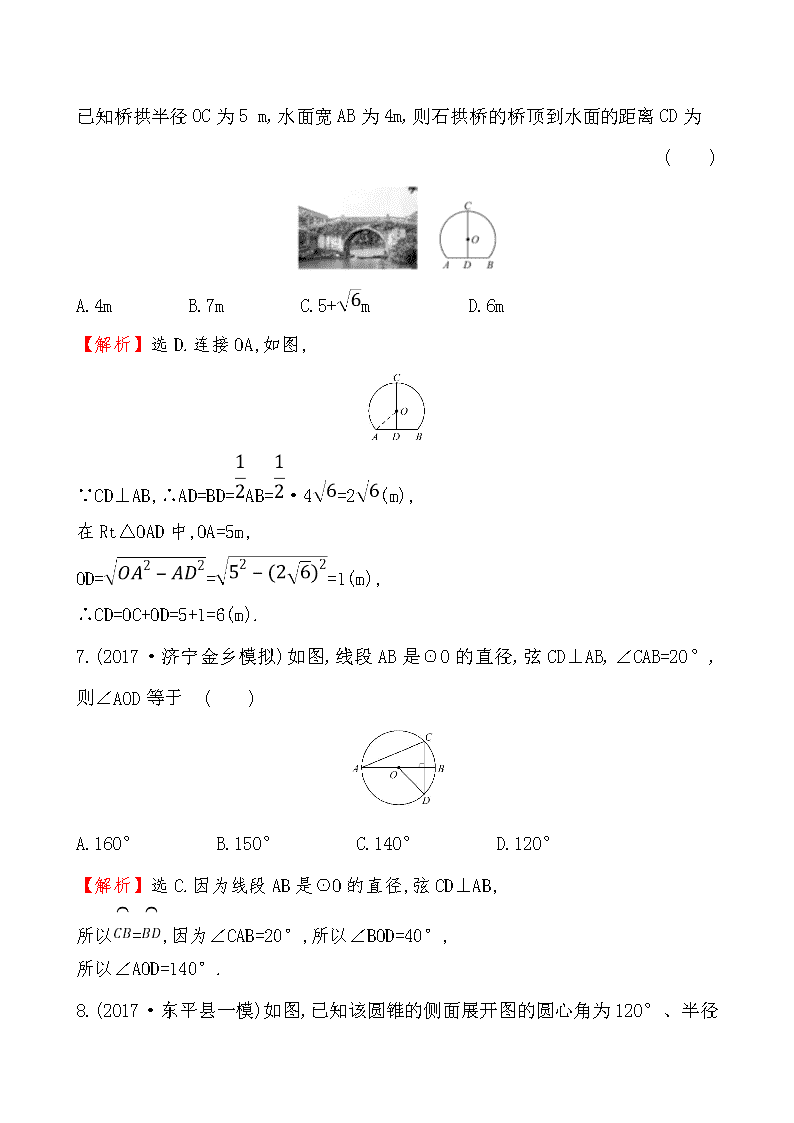6.温州是著名水乡,河流遍布整个城市.某河流上建有一座美丽的石拱桥(如图).已知桥拱半径OC为‎5 m,水面宽AB为‎4‎m,则石拱桥的桥顶到水面的距离CD为　‎ ‎(　　)‎ A‎.4‎m B‎.7m C.5+m D‎.6m ‎【解析】选D.连接OA,如图,‎ ‎∵CD⊥AB,∴AD=BD=AB=·4=2(m),‎ 在Rt△OAD中,OA=‎5m,‎ OD===1(m),‎ ‎∴CD=OC+OD=5+1=6(m).‎ ‎7.(2017·济宁金乡模拟)如图,线段AB是☉O的直径,弦CD⊥AB,∠CAB=20°,则∠AOD等于　(　　)‎ A.160° B.150° C.140° D.120°‎ ‎【解析】选C.因为线段AB是☉O的直径,弦CD⊥AB,‎ 所以=,因为∠CAB=20°,所以∠BOD=40°,‎ 所以∠AOD=140°.‎ ‎8.(2017·东平县一模)如图,已知该圆锥的侧面展开图的圆心角为120°‎ ‎、半径长为6,圆锥的高与母线的夹角为α,则　(　　)‎ A.圆锥的底面半径为3‎ B.tanα=‎ C.圆锥的表面积为12π D.该圆锥的主视图的面积为8‎ ‎【解析】选D.设圆锥的底面半径为r,高为h.由题意:2πr=,解得r=2,h==4,‎ 所以tanα==,圆锥的主视图的面积=×4×4=8,表面积=4π+π×2×6=16π.所以选项A,B,C错误,D正确.‎ ‎9.小明不慎把家里的圆形镜子打碎了,其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的一块碎片应该是　(　　)‎ A.第①块　　 B.第②块　　 C.第③块　 　D.第④块 ‎【解析】选A.第①块出现一段完整的弧,可在这段弧上任做两条弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.‎ ‎10.(2017·东平县一模)如图,☉O的半径OD⊥弦AB于点C,连接AO并延长交☉O于点E,连接EC.若AB=8,CD=2,则EC的长为　(　　)‎ A.2 B.8‎ C.2 D.2‎ ‎【解析】选D.因为☉O的半径OD⊥弦AB于点C,AB=8,所以AC=AB=4,设☉O的半径为r,则OC=r-2,在Rt△AOC中,因为AC=4,OC=r-2,所以OA2=AC2+OC2,即r2=42+(r-2)2,解得r=5,所以AE=2r=10,连接BE,因为AE是☉O的直径,‎ 所以∠ABE=90°,在Rt△ABE中,因为AE=10,AB=8,‎ 所以BE===6,‎ 在Rt△BCE中,因为BE=6,BC=4,‎ 所以CE===2.‎ ‎11.如图,线段AB是☉O的直径,点C,D为☉O上的点,过点C作☉O的切线交AB的延长线于点E,若∠E=50°,则∠CDB等于　(　　)‎ A.20° B.25° C.30° D.40°‎ ‎【解析】选A.连接OC,‎ ‎∵CE是☉O的切线,‎ ‎∴∠OCE=90°,‎ ‎∵∠E=50°,‎ ‎∴∠COE=90°-50°=40°,‎ ‎∴∠CDB=∠COE=20°.‎ ‎12.(2017·胶州市一模)如图,AB是☉O的直径,AC与☉O相切于点A,连接OC交☉O于点D,作DE∥AB交☉O于点E,连接AE,若∠C=40°,则∠E等于　(　　)‎ A.40° B.50° C.20° D.25°‎ ‎【解析】选D.因为AC与圆O相切,所以AC⊥AB,在Rt△AOC中,∠C=40°,所以∠AOC=50°,因为∠AOC与∠AED都对,所以∠E=∠AOC=25°.‎ ‎13.如图,AB是☉O的弦,半径OC经过AB的中点D,CE∥AB,点F在☉O上,连接CF,BF,下列结论中,不正确的是　(　　)‎ A.∠F=∠AOC B.AB⊥BF C.CE是☉O的切线 D.=‎ ‎【解析】选B.A,∵半径OC经过AB的中点D,‎ ‎∴=,‎ ‎∴∠F=∠AOC,故此结论正确,此选项不合题意;‎ B,由于F点不确定,无法得出AB⊥BF,故此选项不正确;‎ C,∵半径OC经过AB的中点D,‎ ‎∴CO⊥AB,‎ ‎∵CE∥AB,‎ ‎∴∠OCE=90°,‎ ‎∴CE是☉O的切线,故此结论正确,不合题意;‎ D,由选项A得,=,故此结论正确,此选项不合题意.‎ ‎14.圆I是三角形ABC的内切圆,D,E,F为3个切点,若∠DEF=52°,则∠A的度数为　(　　)‎ A.68° B.52° C.76° D.38°‎ ‎【解析】选C.∵圆I是三角形ABC的内切圆,‎ ‎∴ID⊥AB,IF⊥AC,‎ ‎∴∠IDA=∠IFA=90°,‎ ‎∴∠A+∠DIF=180°,‎ ‎∵∠DIF=2∠DEF=2×52°=104°,‎ ‎∴∠A=180°-104°=76°.‎ ‎15.(2016·吉林中考)如图,阴影部分是两个半径为1的扇形.若α=120°,β=‎ ‎60°,则大扇形与小扇形的面积之差为　(　　)‎ A. B. C. D.‎ ‎【解析】选B.-=.‎ ‎16.如图,☉O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是　(　　)‎ A.R2-r2=a2‎ B.a=2Rsin 36°‎ C.a=2rtan 36°‎ D.r=Rcos 36°‎ ‎【解析】选A.∵☉O是正五边形ABCDE的外接圆,‎ ‎∴∠BOC=×360°=72°,‎ ‎∴∠1=∠BOC=×72°=36°,‎ R2-r2==a2,‎ a=Rsin 36°,‎ a=2Rsin 36°;‎ a=rtan 36°,‎ a=2rtan 36°,‎ cos 36°=,‎ r=Rcos 36°,‎ 所以,关系式错误的是R2-r2=a2.‎ ‎17.一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么B点从开始至结束所走过的路径长度为　(　　)‎ A. B. C.4 D.2+‎ ‎【解析】选B.如题图:BC=AB=AC=1,‎ ‎∠BCB′=120°,‎ ‎∴B点从开始至结束所走过的路径长度为2×‎ ‎=2×=π.‎ ‎18.如图,已知点P是半径为1的☉A上一点,延长AP到C,使PC=AP,以AC为对角线作▱ABCD,若AB=,则▱ABCD面积的最大值为　(　　)‎ A.2 B. C.2 D.3‎ ‎【解析】选C.由☉A半径为1可知AP=1,因为PC=AP,所以AC=2,以AC为对角线作▱ABCD,▱ABCD面积是△ABC面积的2倍,求▱ABCD面积的最大值即求△ABC面积的最大值,AB=,所以当AB⊥AC时,△ABC面积最大.‎ ‎△ABC面积=,∴▱ABCD面积=2.‎ ‎19.(2017·重庆中考A卷)如图,矩形ABCD的边AB=1,BE平分∠ABC,交AD于点E,若点E是AD的中点,以点B为圆心,BE为半径画弧,交BC于点F,则图中阴影部分的面积是　(　　)‎ A.2- B.-‎ C.2- D.-‎ ‎【解析】选B.因为矩形ABCD的边AB=1,BE平分∠ABC,‎ 所以∠ABE=∠EBF=45°,AD∥BC,所以∠AEB=∠CBE=45°,‎ 所以AB=AE=1,BE=,因为点E是AD的中点,所以AE=ED=1,‎ 所以图中阴影部分的面积=S矩形ABCD-S△ABE-S扇形EBF=1×2-×1×1-=-.‎ ‎20.如图,正方形ABCD和正三角形AEF都内接于☉O,EF与BC,CD分别相交于点G,H,则的值是(　　)‎ A. B. C. D.2‎ ‎【解析】选C.连接AC,EO,AC与EF交于点Q,由四边形ABCD是内接于☉O的正方形得∠ACB=45°,∠B=90°,AC过圆心O,又正三角形AEF内接于☉O,AC是直径,故∠OAE=30°,AC⊥EF.设半径为r,则AE=r,OQ=,又OC =r,所以CQ=,HG=r,==.‎ 二、填空题(本大题共4小题,满分12分,只要求填写最后结果,每小题填对得3分)‎ ‎21.(2017·曹县二模)如图,半径为3的☉A经过原点O和点C(0,2),B是☉O上一点,则tan∠OBC为________.‎ ‎【解析】作直径CD,在Rt△OCD中,CD=6,OC=2,则OD==4,‎ tan∠CDO==,由圆周角定理得,∠OBC=∠CDO,则tan∠OBC=.‎ 答案:‎ ‎22.(2017·天桥区一模)在Rt△ABC中,∠C=90°,AC=6,BC=8,点D在AB上,若以点D为圆心,AD为半径的圆与BC相切,则☉D的半径为________.‎ ‎【解析】过点D作DE⊥BC于点E,因为∠C=90°,所以DE∥AC,‎ 所以△BDE∽△BAC,所以=,设☉D的半径为r,‎ 因为AC=6,BC=8,所以AB=10,即=,解得r=.‎ 答案:‎ ‎23.如图,在平行四边形ABCD中,以对角线AC为直径的☉O分别交BC,CD于点M,N.若AB=13,BC=14,CM=9,则MN的长度为________.‎ ‎【解析】连接AM,AN,‎ ‎∵AC是☉O的直径,‎ ‎∴∠AMC=90°,∠ANC=90°,‎ ‎∵AB=13,BM=BC-CM=5,‎ ‎∴AM==12,‎ ‎∵CM=9,‎ ‎∴AC==15,‎ ‎∵∠MCA=∠MNA,‎ ‎∠MCA=∠CAD,‎ ‎∴∠MNA=∠CAD,‎ ‎∵∠AMN=∠ACN,‎ ‎∴△NMA∽△ACD,‎ ‎∴AM∶MN=DC∶CA,‎ ‎∴12∶MN=13∶15,‎ ‎∴MN=.‎ 答案:‎ ‎24.(2016·河南中考)如图,在扇形AOB中,∠AOB=90°,以点A为圆心,OA的长为半径作交于点C,若OA=2,则阴影部分的面积为________.‎ ‎【解析】连接OC,AC,由题意得,OA=OC=AC=2,‎ ‎∴△AOC为等边三角形,∠BOC=30°,‎ ‎∴扇形COB的面积为:=π,‎ ‎△AOC的面积为:×2×=,‎ 扇形AOC的面积为:=,‎ 则阴影部分的面积为:π+-=-π.‎ 答案:-π 三、解答题(本大题共5个小题,满分48分.解答应写出必要的文字说明、证明过程或推演步骤)‎ ‎25.(8分)已知:如图,在☉O中,弦CD垂直于直径AB,垂足为点E,如果∠BAD=‎ ‎30°,且BE=2,求弦CD的长.‎ ‎【解析】连接OD,设☉O的半径为r,则OE=r-2,‎ ‎∵∠BAD=30°,‎ ‎∴∠DOE=60°,‎ ‎∵CD⊥AB,‎ ‎∴CD=2DE,∠ODE=30°,‎ ‎∴OD=2OE,即r=2(r-2),解得r=4;‎ ‎∴OE=4-2=2,‎ ‎∴DE===2,‎ ‎∴CD=2DE=4.‎ ‎26.(8分)(2017·曹县二模)如图,AB是☉O的直径,C为☉O上一点,PC切☉O于点C,AE⊥PC交PC的延长线于点E,AE交☉O于点D,PC与AB的延长线相交于点P,连接AC,BC.‎ ‎(1)求证:AC平分∠BAD.‎ ‎(2)若PB∶PC=1∶2,PB=4,求AB的长.‎ ‎【解析】(1)如图所示:连接OC.‎ 因为PC是☉O的切线,所以OC⊥EP.‎ 又因为AE⊥PC,所以AE∥OC,所以∠EAC=∠ACO.‎ 又因为∠ACO=∠OAC,所以∠EAC=∠OAC.‎ 所以AC平分∠BAD.‎ ‎(2)因为AB是☉O的直径,所以∠ACB=90°,‎ 所以∠BAC+∠ABC=90°.‎ 因为OB=OC,所以∠OCB=∠ABC.‎ 因为∠PCB+∠OCB=90°,所以∠PCB=∠PAC.‎ 因为∠P=∠P,所以△PCA∽△PBC,‎ 所以=,所以PA==16.‎ 所以AB=PA-PB=16-4=12.‎ ‎27.(10分)(2017·威海模拟)如图,已知AB是☉O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.‎ ‎(1)求证:EF是☉O的切线.‎ ‎(2)求证:AC2=AD·AB.‎ ‎(3)若☉O的半径为2,∠ACD=30°,求图中阴影部分的面积.‎ ‎【解析】(1)连接OC,‎ 因为OA=OC,所以∠BAC=∠OCA,‎ 因为∠DAC=∠BAC,所以∠OCA=∠DAC,所以OC∥AD,‎ 因为AD⊥EF,所以OC⊥EF,‎ 因为OC为半径,所以EF是☉O的切线.‎ ‎(2)连接BC,‎ 因为AB为☉O直径,AD⊥EF,所以∠BCA=∠ADC=90°,‎ 因为∠DAC=∠BAC,所以△ACB∽△ADC,所以=,‎ 所以AC2=AD·AB.‎ ‎(3)因为∠ACD=30°,∠ADC=90°,‎ 所以∠CAD=∠OCA=60°,所以△AOC为等边三角形,‎ 所以AC=OC=OA=2,在Rt△ACD中,∠ACD=30°,‎ 所以AD=AC=1,根据勾股定理得:CD=.‎ 所以S阴影=S△ACD-(S扇形AOC-S△AOC)=×1×-=-.‎ ‎28.(10分)(2016·江西中考)如图,AB是☉O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PE⊥AB,垂足为E,射线EP交于点F,交过点C的切线于点D.‎ ‎(1)求证:DC=DP.‎ ‎(2)若∠CAB=30°,当F是 的中点时,判断以A,O,C,F为顶点的四边形是什么特殊四边形?说明理由.‎ ‎【解析】(1)如图1‎ 连接OC,∵CD是☉O的切线,‎ ‎∴OC⊥CD,　∴∠OCD=90°,‎ ‎∴∠DCA=90°-∠OCA .‎ 又PE⊥AB,点D在EP的延长线上,‎ ‎∴∠DEA=90°,‎ ‎∴∠DPC=∠APE=90°-∠OAC.‎ ‎∵OA=OC,∴∠OCA=∠OAC.‎ ‎∴∠DCA=∠DPC,‎ ‎∴DC=DP.‎ ‎(2)如图2,四边形AOCF是菱形.‎ 连接CF,AF,‎ ‎∵F是的中点,‎ ‎∴=,‎ ‎∴AF=FC.‎ ‎∵∠BAC=30°,∴∠BOC=60°,‎ 又∵AB是☉O的直径,=‎ ‎∴∠AOC=120°,‎ ‎∠ACF=∠FAC=30°,‎ ‎∵OA=OC,∴∠OCA=∠BAC=30°.‎ ‎∴△OAC≌△FAC(ASA).‎ ‎∴AF=OA.‎ ‎∴AF=FC=OC=OA,‎ ‎∴四边形AOCF是菱形.‎ ‎29.(12分)如图,已知AB为☉O的直径,F为☉O上一点,AC平分∠BAF且交☉O于点C,过点C作CD⊥AF于点D,延长AB,DC交于点E,连接BC,CF.‎ ‎(1)求证:CD是☉O的切线.‎ ‎(2)若AD=6,DE=8,求BE的长.‎ ‎(3)求证:AF+2DF=AB.‎ ‎【解析】(1)连接OC,‎ ‎∵AB为☉O的直径,∴∠ACB=90°,‎ ‎∵CD⊥AF,∴∠D=90°,‎ ‎∴∠ACB=∠D,‎ ‎∵AC平分∠BAF,∴∠BAC=∠CAD,‎ ‎∴△ABC∽△ACD,∴∠ABC=∠ACD,‎ ‎∵OB=OC,∴∠OBC=∠OCB,‎ ‎∴∠OCB=∠ACD,‎ ‎∴∠ACO+∠ACD=∠OCB+∠ACO=90°,‎ ‎∴∠OCD=90°,‎ ‎∴CD是☉O的切线.‎ ‎(2)∵AD=6,DE=8,‎ ‎∴AE==10,‎ ‎∵∠OCE=∠ADE,∠E=∠E,‎ ‎∴△OCE∽△ADE,‎ ‎∴=,‎ 设☉O的半径为r.‎ 即=,‎ ‎∴r=,‎ ‎∴BE=10-=.‎ ‎(3)过C作CG⊥AE于点G,‎ 在△ACG与△ACD中,‎ ‎,‎ ‎∴△ACG≌△ACD,‎ ‎∴AG=AD,CG=CD,‎ ‎∵BC=CF,‎ 在Rt△BCG与Rt△FCD中,‎ ‎∴Rt△BCG≌Rt△FCD,‎ ‎∴BG=FD,‎ ‎∴AF+2DF=AD+DF=AG+GB=AB,‎ 即AF+2DF=AB.‎