中考模拟示范卷 5页

‎2019年最新中考模拟示范卷•数学(四)‎ 说明:本卷共有六个大题，23个小题，全卷满分120 分，考试时间120分钟.‎ 一、选择题(本大题共6小题，每小题3分，共18分.每小题只有一个正确选项)‎ ‎1.下列实数中，是无理数的是( )‎ A. B. C. D.1.4142365‎ ‎2.下列计算正确的是( )‎ A.a2+2a2 = 3a B.a3·a2=a6‎ C.a3÷a4=a-1(a≠0) D.(2a+b)2= 4a2+b2‎ ‎3.一个带有正方形孔洞和圆形孔洞的儿童玩具如图所示(正方形的边长和圆形的直径相等)，那么该玩具的主视图为( )‎ ‎ ‎ 4. 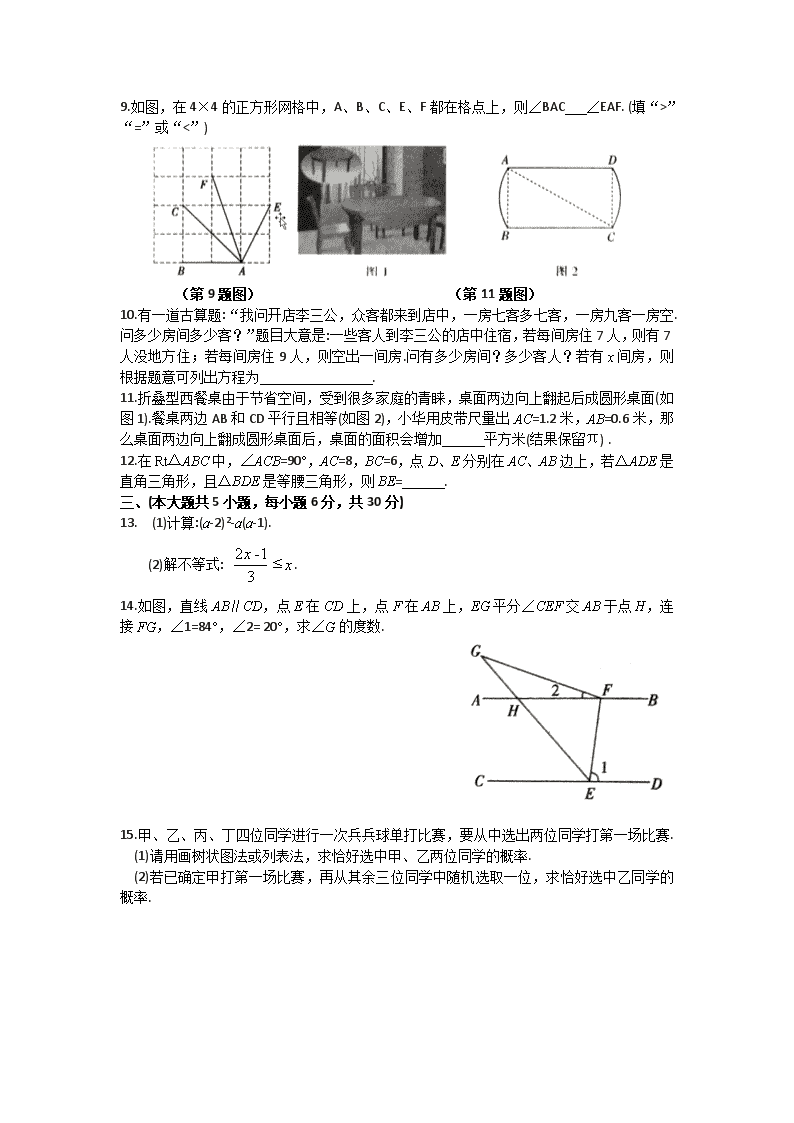某高中体育特长班21名同学的身高统计如下表:‎ ‎ ‎ 则该班21名同学身高的众数和中位数分别是( )‎ A.186，186 B.186，188 C 192，187 D.208，188‎ ‎5.如图，将正方形OABC放在平面直角坐标系中，O是原点，点A的坐标为(1，)，则点B的坐标为( )‎ A.(-1，)‎ B.(-，1)‎ C.(1-，+1)‎ D.(-，+1) ‎ ‎6.已知抛物线y=x2+bx+c与x轴交于点(x1，0)与(x2，0)，其中x1m+n C.x1·x2=m·n-3 D.m”“=”或“<”)‎ ‎ ‎ ‎（第9题图） （第11题图）‎ ‎10.有一道古算题:“我问开店李三公，众客都来到店中，一房七客多七客，一房九客一房空.问多少房间多少客？”题目大意是:一些客人到李三公的店中住宿，若每间房住7人，则有7人没地方住；若每间房住9人，则空出一间房.问有多少房间？多少客人？若有x间房，则根据题意可列出方程为 .‎ ‎11.折叠型西餐桌由于节省空间，受到很多家庭的青睐，桌面两边向上翻起后成圆形桌面(如图1).餐桌两边AB和CD平行且相等(如图2)，小华用皮带尺量出AC=1.2米，AB=0.6米，那么桌面两边向上翻成圆形桌面后，桌面的面积会增加 平方米(结果保留π) .‎ ‎12.在Rt△ABC中，∠ACB=90°，AC=8，BC=6，点D、E分别在AC、AB边上，若△ADE是直角三角形，且△BDE是等腰三角形，则BE= .‎ 三、(本大题共5小题，每小题6分，共30分)‎ ‎13. (1)计算:(a-2)2-a(a-1).‎ ‎(2)解不等式: .‎ ‎14.如图，直线AB∥CD，点E在CD上，点F在AB上，EG平分∠CEF交AB于点H，连接FG，∠1=84°，∠2= 20°，求∠G的度数.‎ ‎ ‎ ‎15.甲、乙、丙、丁四位同学进行一次兵兵球单打比赛，要从中选出两位同学打第一场比赛.‎ ‎(1)请用画树状图法或列表法，求恰好选中甲、乙两位同学的概率.‎ ‎(2)若已确定甲打第一场比赛，再从其余三位同学中随机选取一位，求恰好选中乙同学的概率.‎ ‎16.在△ABC中，∠C=50°，请根据下列条件，用无刻度的直尺画一个直角三角形，使其一个顶点为A，且一个内角为50°.‎ ‎(1)如图1，A、B、C三点都在⊙O上.‎ ‎(2)如图2，A、C两点在⊙O上，点B在⊙O内.‎ ‎ ‎ ‎17.在一次综合实践课上，同学们为教室窗户设计一个遮阳篷，小明同学绘制的设计图如图所示，其中AB表示窗户，且AB=2米，ABCD表示直角遮阳篷，已知当地一年中正午时刻的太阳光与水平线CD的最小夹角∠PDN= 18.6°，最大夹角∠MDN=64.5°.请你据以上数据，帮助小明同学计算出遮阳篷中CD的长.‎ ‎(结果精确到0.1米；参考数据：sin 18. 6°≈0.32，tan 18.6°≈0.34，sin 64.5°≈0.90，tan64.5°≈2.1)‎ ‎ ‎ 四、(本大题共3小题，每小题8分，共24分)‎ ‎18.随着移动互联网的迅速发展和普及，淘宝购物的使用极大地方便了人们的生活.小明在某小区随机抽取部分居民“就使用淘宝购物的情况”进行了一次抽样调查，下面是他利用收集到的数据绘制成的两幅不完整的统计图，请你根据图中提供的信息解答下列问题:‎ ‎(1)问：参与本次问卷调查的居民有多少人？‎ ‎(2)请把条形统计图补充完整.‎ ‎(3)求扇形统计图中“从不使用”部分所对应的扇形的圆心角的度数.‎ ‎ ‎ ‎19.如图，双曲线(x>0)经过Rt△AOB斜边的中点P，交直角边AB于点Q，连接OQ，‎ 点A的坐标为(8，4).‎ ‎(1)求直线OQ的解析式.‎ ‎(2)求sin∠QOA的值.‎ ‎20.某公司投入4. 144万元购买了某种产品的技术专利，为生产该产品又投人12万元购买了一台新机器，投入生产后发现，生产件该产品需要50元的成本，又知该产品每件的售价是130元.‎ ‎(1)这家公司至少需要生产多少件该产品才能开始盈利？‎ ‎(2)已知这台机器可再生产产品的数量y(件)与共生产的产品数量x(件)之间的函数关系式为y=-，则这台机器正常报废时，能盈利多少万元？‎ 五、(本大题共2小题，每小题9分，共18分)‎ ‎21.如图，△ABC内接于⊙O，AB为直径，∠BAC的平分线交⊙O于点D，过点D作DE⊥AC分别交AC、AB的延长线于点E、F.‎ ‎(1)求证：EF是⊙O的切线.‎ ‎(2)若AC= 4，CE=2，求弧BC的长度(结果保留π)‎ ‎ ‎ ‎22.如图1，在矩形ABCD中，AD> AB，将矩形沿着对角线BD向上折叠，顶点C落到点E处，BE交AD于点F.‎ ‎(1)求证：BF= DF.‎ ‎(2)如图2，∠BFD的平分线交BD于点O，交BC于点G，连接DG.‎ ‎①判断四边形BFDG的形状，并说明理由；‎ ‎②若AB=6，tan∠ABF=，求FG的长.‎ ‎ ‎ 六、(本大题共12分)‎ ‎23.如图，二次函数l1：y=ax2+2ax+a- 2(a>0)和二次函数l2：y=-a(x-2)2+2(a>0)图象的顶点分别为M、N，与x轴分别交于A、B两点(点A在点B的左边)和C、D两点(点C在点D的左边).‎ ‎(1)函数y=ax2+2ax+a- 2(a>0)图象的顶点M的坐标为 ；当二次函数l1，l2的y值同时随着x的增大而增大时，x的取值范围是 .‎ ‎(2)当AD=MN时，求a的值，并直接判断出四边形AMDN的形状.‎ ‎(3)当B、C是线段AD的三等分点时，求a的值.‎ ‎ ‎