中考圆有关的动点几何压轴题 23页

北辰教育学科老师辅导讲义 学员姓名： 年级：初三 辅导科目：数学 学科教师：陆军 授课日期 授课时段 授课主题 中考25题压轴题之涉及圆问题分析 教学内容 与圆有关的常见辅助线添加方法 辅助线秘诀一 已知直径或作直径，我们要想到两件事：‎ ‎1；直径上有一个隐藏的中点（圆心）‎ ‎2；利用圆周角定理构造直角三角形 辅助线秘诀二 作半径 ‎1；连半径，造等腰三角形 ‎2；作过切点的半径 辅助线秘诀三 涉及弦长，弦心距；可造垂径定理的模型，为勾股定理创造条件 辅助线秘诀四 切线的证明 ‎1；有交点：连半径，证垂直 ‎2；无交点：作垂直，证半径 辅助线秘诀五 已知数圆心角度数，要想到同弧所对圆周角度数，反之亦然。‎ 辅助线秘诀六 出现等弧问题时，我们要想到 ‎1；在同圆或等圆中相等的弧所对的弦相等，弦心距也相等。‎ ‎2；在同圆或等圆中相等的弧所对的圆心角，圆周角也相等。‎ 辅助线秘诀七 已知三角比或求某个角的三角比，要想到把角放在直角三角形中，没有作垂直。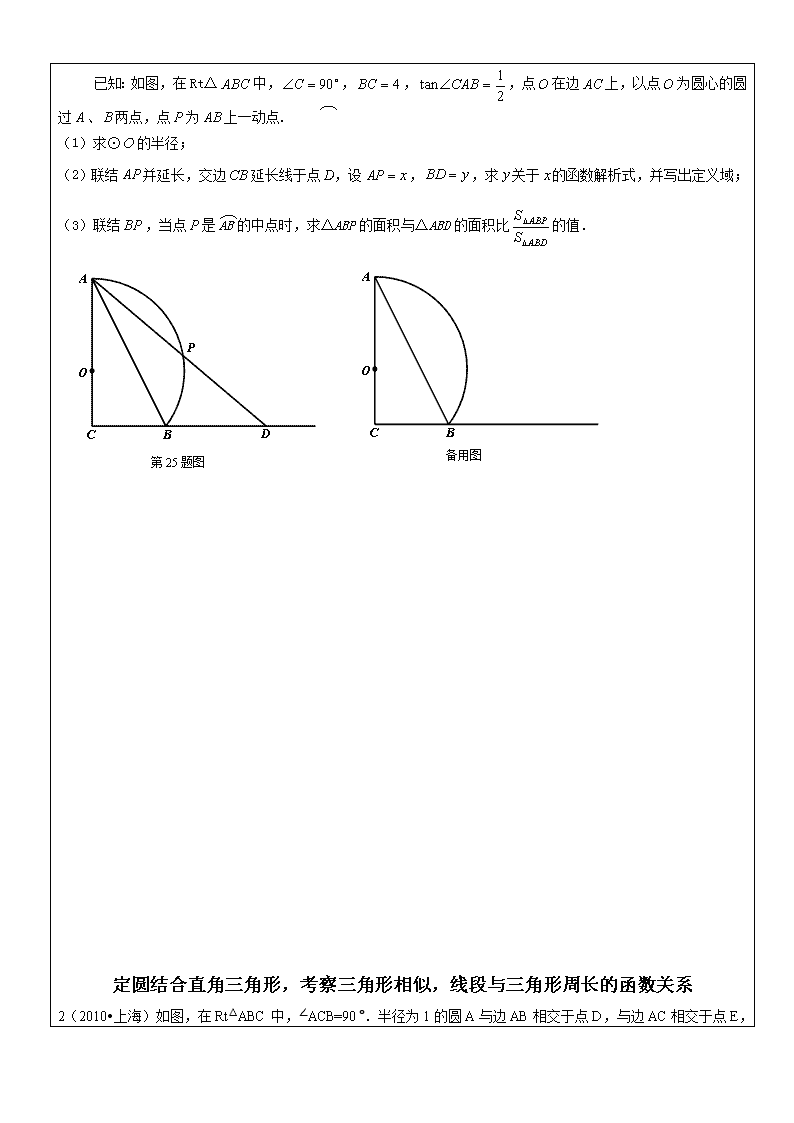‎ 注意；同角或等角的三角比相同 辅助线秘诀八 圆中出现内接正多边形时；‎ 作边心距，抓住一个直角三角形来解决 辅助线秘诀九 已知两圆相切，常用的辅助线是；‎ ‎1；作公切线，连接过切点的半径得到垂直关系 ‎2；作连心线 辅助线秘诀十 已知两圆相交，常用的辅助线是；‎ ‎1；作两圆公切弦 ‎2；作连心线 例题讲解 定圆结合直角三角形，考察两线段函数关系，三角形面积比值 ‎1（本题满分14分，其中第（1）小题4分，第（2）、（3）小题各5分）‎ 已知：如图，在Rt△中，，，，点在边上，以点为圆心的圆过、两点，点为上一动点.‎ ‎（1）求⊙的半径；‎ ‎（2）联结并延长，交边延长线于点，设，，求关于的函数解析式，并写出定义域；‎ 备用图 第25题图 ‎（3）联结，当点是AB的中点时，求△ABP的面积与△ABD的面积比的值．‎ 定圆结合直角三角形，考察三角形相似，线段与三角形周长的函数关系 ‎2‎ ‎（2010•上海）如图，在Rt△ABC中，∠ACB=90°．半径为1的圆A与边AB相交于点D，与边AC相交于点E，连接DE并延长，与线段BC的延长线交于点P．‎ ‎（1）当∠B=30°时，连接AP，若△AEP与△BDP相似，求CE的长；‎ ‎（2）若CE=2，BD=BC，求∠BPD的正切值；‎ ‎（3）若tan∠BPD=，设CE=x，△ABC的周长为y，求y关于x的函数关系式．‎ 定圆结合直角三角形，考察两线段函数关系，圆心距，存在性问题 ‎3．如图，在半径为5的⊙O中，点A、B在⊙O上，∠AOB=90°，点C是弧AB上的一个动点，AC与OB的延长线相交于点D，设AC=x，BD=y．‎ ‎（1）求y关于x的函数解析式，并写出它的定义域；‎ ‎（2）如果⊙O1与⊙O相交于点A、C，且⊙O1与⊙O的圆心距为2，当BD=OB时，求⊙O1的半径；‎ ‎（3）是否存在点C，使得△DCB∽△DOC？如果存在，请证明；如果不存在，请简要说明理由．‎ 定圆中结合平行线，弧中点，考察两线段函数关系，圆相切 ‎4（本题满分14分，第（1）小题6分，第（2）小题2分，第（3）小题6分）‎ 在半径为4的⊙O中，点C是以AB为直径的半圆的中点，OD⊥AC，垂足为D，点E是射线AB上的任意一点，DF//AB，DF与CE相交于点F，设EF=，DF=． ‎ （1） 如图1，当点E在射线OB上时，求关于的函数解析式，并写出函数定义域；‎ （2） 如图2，当点F在⊙O上时，求线段DF的长；‎ （3） 如果以点E为圆心、EF为半径的圆与⊙O相切，求线段DF的长．‎ A B E F C D O ‎（第25题图1）‎ A B E F C D O 动圆结合直角梯形，考察圆相切和相似 ‎5（14分）（2014•金山区二模）如图，已知在梯形ABCD中，AD∥BC，AB⊥BC，AB=4，AD=3，sin∠DCB=，P是边CD上一点（点P与点C、D不重合），以PC为半径的⊙P与边BC相交于点C和点Q．‎ ‎（1）如果BP⊥CD，求CP的长；‎ ‎（2）如果PA=PB，试判断以AB为直径的⊙O与⊙P的位置关系；‎ ‎（3）联结PQ，如果△ADP和△BQP相似，求CP的长．‎ 动圆结合内切直角三角形，考察相似，两线段函数关系 ‎ 6. 2005中考（本题满分12分，每小题满分各为4分）‎ 在△ABC中，∠ABC＝90°，AB＝4，BC＝3，O是边AC上的一个动点，以点O为圆心作半圆，与边AB相切于点D，交线段OC于点E，作EP⊥ED，交射线AB于点P，交射线CB于点F。‎ （1） 如图8，求证：△ADE∽△AEP；‎ （2） 设OA＝x，AP＝y，求y关于x的函数解析式，并写出它的定义域；‎ （1） 当BF＝1时，求线段AP的长.‎ 动圆结合定圆，考察两线段函数关系，圆相切 ‎7.（本题满分14分，第（1）小题4分，第（2）小题5分，第（3）小题5分）‎ 如图1，已知的半径长为3，点是上一定点，点为上不同于点的动点。‎ ‎（1）当时，求的长；‎ ‎（2）如果过点、，且点在直线上（如图2），设，，求关于的函数关系式，并写出函数的定义域；‎ ‎（3）在（2）的条件下，当时（如图3），存在与相内切，同时与相外切，且，‎ ‎ 试求的半径的长。‎ 动圆结合定圆，考察两线段函数关系，相似，勾股定理，圆相交和正多边形 ‎8．如图1，已知⊙O的半径长为1，PQ是⊙O的直径，点M是PQ延长线上一点，以点M为圆心作圆，与⊙O交于A、B两点，连接PA并延长，交⊙M于另外一点C．‎ ‎（1）若AB恰好是⊙O的直径，设OM=x，AC=y，试在图2中画出符合要求的大致图形，并求y关于x的函数解析式；‎ ‎（2）连接OA、MA、MC，若OA⊥MA，且△OMA与△PMC相似，求OM的长度和⊙M的半径长；‎ ‎（3）是否存在⊙M，使得AB、AC恰好是一个正五边形的两条边？若存在，试求OM的长度和⊙M的半径长；若不存在，试说明理由．‎ 动圆结合三角形，考察相似，线段比，圆位置关系 ‎9.2006中考25.（本题满分14分，第（1）小题满分4分，第（2）小题满分7分，第（3）小题满分3分）‎ 已知点P在线段AB上，点O在线段AB的延长线上。以点O为圆心，OP为半径作圆，点C是圆O上的一点。‎ ‎（1）如图，如果AP=2PB，PB=BO。求证：△CAO∽△BCO；‎ ‎（2）如果AP=m（m是常数，且m>1），BP=1，OP是OA、OB的比例中项。当点C在圆O上运动时，求AC：BC的值（结果用含m的式子表示）；‎ ‎（3）在（2）的条件下，讨论以BC为半径的圆B和以CA为半径的圆C的位置关系，并写出相应m的取值范围。‎ ‎1解：‎ ‎（1）联结OB．‎ 在Rt△中，，‎ ‎，，‎ ‎∴AC=8．………………………………（1分）‎ 设，则．‎ 在Rt△中，，‎ ‎∴．……………………………………………………………（2分）‎ 解得，即⊙的半径为5．………………………………………………（1分）‎ ‎（2）过点O作OH⊥AD于点H．‎ ‎ ∵OH过圆心，且OH⊥AD．‎ ‎∴．………………………（1分）‎ 在Rt△中，可得 即．…………（1分）‎ 在△和△中，‎ ‎，，∴△AOH∽△ADC．……………………（1分）‎ ‎∴．即．‎ 得．………………………………………………………（1分）‎ 定义域为．…………………………………………………………（1分）‎ ‎（3）∵是AB的中点，∴AP=BP．∵AO=BO，∴PO垂直平分AB．‎ 设，可求得，，，‎ ‎，，．‎ ‎∴．‎ ‎∴△ABP∽△ABD．…………………………（1分）‎ ‎∴．………………………（1分）‎ ‎ ．‎ 由AP=BP可得．‎ ‎∴．‎ ‎∴，即．…………（1分）‎ 由可得，即．………（1分）‎ ‎．……………………………………（1分）‎ ‎2考点：相似三角形的判定与性质；等腰三角形的性质；勾股定理；解直角三角形。‎ 专题：几何综合题；压轴题。‎ 分析：（1）当∠B=30°时，∠A=60°，此时△ADE是等边三角形，则∠PEC=∠AED=60°，由此可证得∠P=∠B=30°；若△AEP与△BDP相似，那么∠EAP=∠EPA=∠B=∠P=30°，此时EP=EA=1，即可在Rt△PEC中求得CE的长；‎ ‎（2）若BD=BC，可在Rt△ABC中，由勾股定理求得BD、BC的长；过C作CF∥DP交AB于F，易证得△ADE∽△AFC，根据得到的比例线段可求出DF的长；进而可通过证△BCF∽△BPD，根据相似三角形的对应边成比例求得BP、BC的比例关系，进而求出BP、CP的长；在Rt△CEP中，根据求得的CP的长及已知的CE的长即可得到∠BPD的正切值；‎ ‎（3）过点D作DQ⊥AC于Q，可用未知数表示出QE的长，根据∠BPD（即∠EDQ）的正切值即可求出DQ的长；在Rt△ADQ中，可用QE表示出AQ的长，由勾股定理即可求得EQ、DQ、AQ的长；易证得△ADQ∽△ABC，根据得到的比例线段可求出BD、BC的表达式，进而可根据三角形周长的计算方法得到y、x的函数关系式．‎ 解答：解：（1）∵∠B=30°，∠ACB=90°，‎ ‎∴∠BAC=60°．‎ ‎∵AD=AE，‎ ‎∴∠AED=60°=∠CEP，‎ ‎∴∠EPC=30°．‎ ‎∴△BDP为等腰三角形．‎ ‎∵△AEP与△BDP相似，‎ ‎∴∠EPA=∠DPB=30°，‎ ‎∴AE=EP=1．‎ ‎∴在Rt△ECP中，EC=EP=；‎ ‎（2）设BD=BC=x．‎ 在Rt△ABC中，由勾股定理，得：‎ ‎（x+1）2=x2+（2+1）2，‎ 解之得x=4，即BC=4．‎ 过点C作CF∥DP．‎ ‎∴△ADE与△AFC相似，‎ ‎∴，即AF=AC，即DF=EC=2，‎ ‎∴BF=DF=2．‎ ‎∵△BFC与△BDP相似，‎ ‎∴，即：BC=CP=4．‎ ‎∴tan∠BPD=．‎ ‎（3）过D点作DQ⊥AC于点Q．‎ 则△DQE与△PCE相似，设AQ=a，则QE=1﹣a．‎ ‎∴且，‎ ‎∴DQ=3（1﹣a）．‎ ‎∵在Rt△ADQ中，据勾股定理得：AD2=AQ2+DQ2‎ 即：12=a2+[3（1﹣a）]2，‎ 解之得．‎ ‎∵△ADQ与△ABC相似，‎ ‎∴．‎ ‎∴．‎ ‎∴△ABC的周长，‎ 即：y=3+3x，其中x＞0．‎ ‎3考点：相似三角形的判定与性质；勾股定理；圆与圆的位置关系。‎ 专题：代数几何综合题；分类讨论。‎ 分析：（1）过⊙O的圆心作OE⊥AC，垂足为E．通过证明△ODE∽△AOE求得，然后将相关线段的长度代入求得y关于x的函数解析式，再由函数的性质求其定义域；‎ ‎（2）当BD=OB时，根据（1）的函数关系式求得y=，x=6．分两种情况来解答O1A的值①当点O1在线段OE上时，O1E=OE﹣OO1=2；②当点O1在线段EO的延长线上时，O1E=OE+OO1=6；‎ ‎（3）当点C为AB的中点时，∠BOC=∠AOC=∠AOB=45°，∠OCA=∠OCB=，然后由三角形的内角和定理求得 ‎∠DCB=45°，由等量代换求得∠DCB=∠BOC．根据相似三角形的判定定理AA证明△DCB∽△DOC．‎ 解答：解：（1）过⊙O的圆心作OE⊥AC，垂足为E，‎ ‎∴AE=，OE=．‎ ‎∵∠DEO=∠AOB=90°，∴∠D=90°﹣∠EOD=∠AOE，∴△ODE∽△AOE．‎ ‎∴，∵OD=y+5，∴．‎ ‎∴y关于x的函数解析式为：．‎ 定义域为：．（1分）‎ ‎（2）当BD=OB时，，．‎ ‎∴x=6．‎ ‎∴AE=，OE=．‎ 当点O1在线段OE上时，O1E=OE﹣OO1=2，．‎ 当点O1在线段EO的延长线上时，O1E=OE+OO1=6，．‎ ‎⊙O1的半径为或．‎ ‎（3）存在，当点C为的中点时，△DCB∽△DOC．‎ 证明如下：∵当点C为的中点时，∠BOC=∠AOC=∠AOB=45°，‎ 又∵OA=OC=OB，∴∠OCA=∠OCB=，‎ ‎∴∠DCB=180°﹣∠OCA﹣∠OCB=45°．‎ ‎∴∠DCB=∠BOC．又∵∠D=∠D，∴△DCB∽△DOC．‎ ‎∴存在点C，使得△DCB∽△DOC．‎ 点评：本题主要考查了圆与圆的位置关系、勾股定理．此题很复杂，解答此题的关键是作出辅助线OE⊥AC，利用相似三角形的判定定理及性质解答，解答（2）时注意分两种情况讨论，不要漏解．‎ ‎4．解：（1）联结OC，∵AC是⊙O的弦，OD⊥AC，∴OD=AD．………………（1分）‎ ‎∵DF//AB，∴CF=EF，∴DF==．…………………（1分）‎ ‎∵点C是以AB为直径的半圆的中点，∴CO⊥AB．………………………（1分）‎ ‎∵EF=，AO=CO=4,∴CE=2,OE=.…（1分）‎ ‎∴. 定义域为．……………（1+1分）‎ ‎（2）当点F在⊙O上时，联结OC、OF，EF=，∴OC=OB=AB=4．（分）‎ ‎∴DF=2+=2+2．………………………………（1分）（3）当⊙E与⊙O外切于点B时，BE=FE．∵，‎ ‎ ∴ ，‎ ‎∴，）．……………………………（1分）‎ ‎ ∴DF=．…………………（1分）‎ 当⊙E与⊙O内切于点B时，BE=FE．∵，‎ ‎ ∴ ，‎ ‎∴，）．………………………………（1分）‎ ‎∴DF=．……………………（1分）‎ 当⊙E与⊙O内切于点A时，AE=FE．∵，‎ ‎ ∴ ，‎ ‎∴，）．……………………………（1分）‎ ‎∴DF=．……………………………………………………………（1分）‎ ‎5.：（1）作DH⊥BC于H，如图1，‎ ‎∵AD∥BC，AB⊥BC，AB=4，AD=3，‎ ‎∴DH=4，BH=3，‎ 在Rt△DHC中，sin∠DCH==，‎ ‎∴DC=5，‎ ‎∴CH==3，‎ ‎∴BC=BH+CH=6，‎ ‎∵BP⊥CD，‎ ‎∴∠BPC=90°，‎ 而∠DCH=∠BCP，‎ ‎∴Rt△DCH∽Rt△BCP，‎ ‎∴=，即=，‎ ‎∴PC=；‎ ‎（2）作PE⊥AB于E，如图2，‎ ‎∵PA=PB，‎ ‎∴AE=BE=AB=2，‎ ‎∵PE∥AD∥BC，‎ ‎∴PE为梯形ABCD的中位线，‎ ‎∴PD=PC，PE=（AD+BC）=（3+6）=，‎ ‎∴PC=BC=，‎ ‎∴EA+PC=PE，‎ ‎∴以AB为直径的⊙O与⊙P外切；‎ ‎（3）如图1，作PF⊥BC于F，则CF=QF，‎ 设PC=x，则DP=5﹣x，‎ ‎∵PF∥DH，‎ ‎∴△CPF∽△CDH，‎ ‎∴=，即=，解得CF=，‎ ‎∴CQ=2CF=，‎ ‎∴BQ=BC﹣CQ=6﹣，‎ ‎∵PQ=PC，‎ ‎∴∠PQC=∠PCQ，‎ ‎∵AD∥BC，‎ ‎∴∠ADP+∠PCQ=180°，‎ 而∠PQC+∠PQB=180°，‎ ‎∴∠ADP=∠PQB，‎ 当△ADP∽△BQP，‎ ‎∴=，即=，‎ 整理得2x2﹣25x+50=0，解得x1=，x2=10（舍去），‎ 经检验x=是原分式方程的解．‎ ‎∴PC=；‎ 当△ADP∽△PQB，‎ ‎∴=，即=‎ 整理得5x2﹣43x+90=0，解得x1=，x2=5（舍去），‎ 经检验x=是原分式方程的解．‎ ‎∴PC=，‎ ‎∴如果△ADP和△BQP相似，CP的长为或．‎ J 7. ‎8.考点：相似三角形的判定与性质；勾股定理；相交两圆的性质；正多边形和圆。‎ 专题：计算题；证明题。‎ 分析：（1）过点M作MN⊥AC，垂足为N，可得，再根据PM⊥AB，又AB是圆O的直径，可得，在Rt△PNM中，再利用即可求得y关于x的函数解析式；‎ ‎（2）设圆M的半径为r，利用勾股定理求出OM，根据△OMA∽△PMC，可得△PMC是直角三角形．然后可得∠CPM、∠PCM都不可能是直角．又利用∠AOM=2∠P≠∠P，可得即若△OMA与△PMC相似，其对应性只能是点O与点C对应、点M与点P对应、点A与点M对应．从而求得OM，然后即可求得⊙M的半径长．‎ ‎（3）假设存在⊙M，使得AB、AC恰好是一个正五边形的两条边，连接OA、MA、MC、AQ，设公共弦AB与直线OM相交于点G，由正五边形求得∠AMB和∠BAC，再利用AB是公共弦，OM⊥AB，∠AMO=36°，从而求得∠AOM=∠AMO，在求证△MAQ∽△MOA，利用相似三角形对应边成比例即可求得．‎ 解答：解：（1）过点M作MN⊥AC，垂足为N，‎ ‎∴，‎ 由题意得：PM⊥AB，又AB是圆O的直径，‎ ‎∴OA=OP=1，‎ ‎∴∠APO=45°，，‎ ‎∴，‎ 在Rt△PNM中，，‎ 又PM=1+x，∠NPM=45°，‎ ‎∴，‎ ‎∴y关于x的函数解析式为（x＞1），‎ ‎（2）设圆M的半径为r，‎ ‎∵OA⊥MA，‎ ‎∴∠OAM=90°，‎ 又∵△OMA∽△PMC，‎ ‎∴△PMC是直角三角形．‎ ‎∵OA=OP，MA=MC，‎ ‎∴∠CPM、∠PCM都不可能是直角．‎ ‎∴∠PMC=90°．‎ 又∵∠AOM=2∠P≠∠P，‎ ‎∴∠AMO=∠P，‎ 即若△OMA与△PMC相似，其对应性只能是点O与点C对应、点M与点P对应、点A与点M对应．‎ ‎∴，即，解得，‎ 从而OM=2，‎ ‎∴OM=2，圆M的半径为．‎ ‎（3）假设存在⊙M，使得AB、AC恰好是一个正五边形的两条边，‎ 连接OA、MA、MC、AQ，设公共弦AB与直线OM相交于点G 由正五边形知，∠BAC=108°，‎ ‎∵AB是公共弦，‎ ‎∴OM⊥AB，∠AMO=36°，‎ 从而∠P=18°，∠AOM=2∠P=36°‎ ‎∴∠AOM=∠AMO ‎∴AM=AO=1，即圆M的半径是1，‎ ‎∵OA=OQ=1，∠AOM=36°‎ ‎∴∠AQO=72°‎ ‎∴∠QAM=∠AQO﹣∠AMO=36°‎ ‎∴△MAQ∽△MOA，‎ ‎∴‎ ‎∵AM=1，MQ=OM﹣1‎ ‎∴，解得：（负值舍去）‎ ‎∴，‎ 所以，存在⊙M，使得AB、AC恰好是一个正五边形的两条边，‎ 此时的，圆M的半径是1．‎ ‎9/．(1)两边一夹角 ‎(2)解：设OP=x，则OB=x-1，OA=x+m，‎ OP=，OB=‎ OA/OC=OC/OB 设圆O与线段AB的延长线相交于点Q，当点c与点P、点Q不重合时，△CAO∽△BCO．‎ AC/BC=OC/OB=OP/OB=m；当点C与点P或点Q重OB合时，可得AC/BC=m，‎ ‎．。．当点C在圆O上运动时，AC:BC=m ‎(3)解：由(2)得，AC>BC，且AC-BC=(m-1)BC(m>1)，‎ AC+BC=(m+1)BC，圆B和圆C的圆心距d=BC，‎ 显然BC<(m+1)BC，．．．圆B和圆C的位置关系只可能相交、内切或内含．‎ 当圆B与圆C相交时，(m-1)BC1，．∴12．‎