中考数学压轴题精选4含答案 8页

一．选择题（共4小题）‎ ‎1．在矩形ABCD中，有一个菱形BFDE（点E，F分别在线段AB，CD上），记它们的面积分别为SABCD和SBFDE，现给出下列命题：①若=，则tan∠EDF=；②若DE2=BD•EF，则DF=2AD，则（　　）‎ A．①是假命题，②是假命题 B．①是真命题，②是假命题 C．①是假命题，②是真命题 D．①是真命题，②是真命题 ‎2．如图，将矩形ABCD沿AF折叠，使点D落在BC边的点E处，过点E作EG∥CD交AF于点G，连接DG．给出以下结论：①DG=DF；②四边形EFDG是菱形；③EG2=GF×AF；④当AG=6，EG=2时，BE的长为，其中正确的结论个数是（　　）‎ A．1 B．2 C．3 D．4‎ ‎3．如图，平行四边形ABCD的顶点C在y轴正半轴上，CD平行于x轴，直线AC交x轴于点E，BC⊥AC，连接BE，反比例函数（x＞0）的图象经过点D．已知S△BCE=2，则k的值是（　　）‎ A．2 B．﹣2 C．3 D．4‎ ‎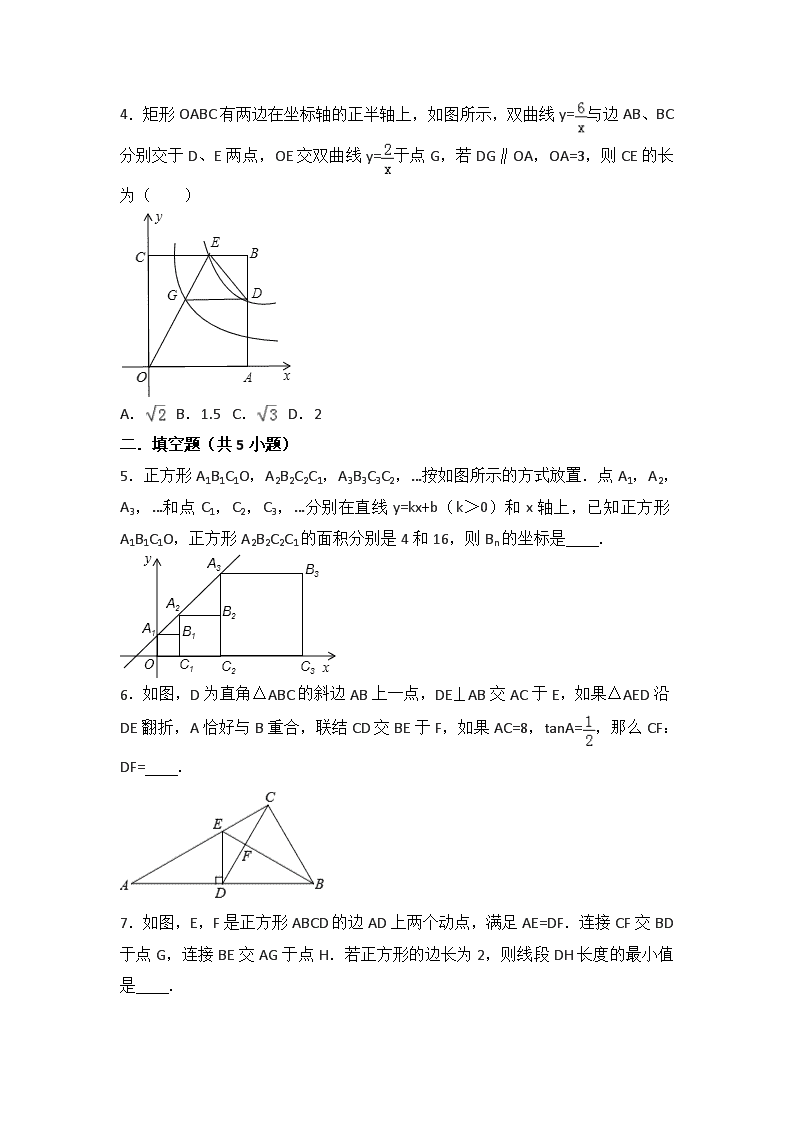4．矩形OABC有两边在坐标轴的正半轴上，如图所示，双曲线y=与边AB、BC分别交于D、E两点，OE交双曲线y=于点G，若DG∥OA，OA=3，则CE的长为（　　）‎ A． B．1.5 C． D．2‎ 二．填空题（共5小题）‎ ‎5．正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图所示的方式放置．点A1，A2，A3，…和点C1，C2，C3，…分别在直线y=kx+b（k＞0）和x轴上，已知正方形A1B1C1O，正方形A2B2C2C1的面积分别是4和16，则Bn的坐标是　　．‎ ‎6．如图，D为直角△ABC的斜边AB上一点，DE⊥AB交AC于E，如果△AED沿DE翻折，A恰好与B重合，联结CD交BE于F，如果AC=8，tanA=，那么CF：DF=　　．‎ ‎7．如图，E，F是正方形ABCD的边AD上两个动点，满足AE=DF．连接CF交BD于点G，连接BE交AG于点H．若正方形的边长为2，则线段DH长度的最小值是　　．‎ ‎8．如图，在菱形ABCD中，AB=5，AC=8，点P是对角线AC上的一个动点，过点P作EF⊥AC分别交AD、AB于点E、F，将△AEF沿EF折叠，点A落在点A′处，当△A′BC是等腰三角形时，AP的长为　　．‎ ‎9．如图，矩形ABCD中，点E，F，G，H分别在边AB，BC，CD，DA上，点P在矩形ABCD内．若AB=4cm，BC=6cm，AE=CG=3cm，BF=DH=4cm，四边形AEPH的面积为5cm2，则四边形PFCG的面积为　　cm2．‎ ‎　‎ 三．解答题（共8小题）‎ ‎10．如图①，在△ABC中，AB=AC，点D，E分别在边BC、AC上，连接DE，且DE=DC．‎ ‎（1）问题发现：若∠ABC=∠EDC=90°，则=　　；‎ ‎（2）拓展探究，若∠ABC=∠EDC=120°，将△EDC绕点C按顺时针方向旋转到如图②所示的位置，则的大小有无变化？若不变，请加以证明；若变化，请求出的值．‎ ‎（3）问题解决：当△EDC旋转到如图③所示的位置时，若∠ABC=∠EDC=2α（0°＜α＜90°），则的值为　　（用含a的式子表示）‎ ‎11．如图，二次函数y=ax2﹣x+2（a≠0）的图象与x轴交于A、B两点，与y轴交于点C，已知点A（﹣4，0）．‎ ‎（1）求抛物线与直线AC的函数解析式；‎ ‎（2）若点D（m，n）是抛物线在第二象限的部分上的一动点，四边形OCDA的面积为S，求S关于m的函数关系；‎ ‎（3）若点E为抛物线上任意一点，点F为x轴上任意一点，当以A、C、E、F为顶点的四边形是平行四边形时，请直接写出满足条件的所有点E的坐标．‎ ‎12．如图（1）所示，E为矩形ABCD的边AD上一点，动点P、Q同时从点B出发，点P以1cm/秒的速度沿折线BE﹣ED﹣DC运动到点C时停止，点Q以2cm/秒的速度沿BC运动到点C时停止．设P、Q同时出发t秒时，△BPQ的面积为ycm2．已知y与t的函数关系图象如图（2）（其中曲线OG为抛物线的一部分，其余各部分均为线段）．‎ ‎（1）试根据图（2）求0＜t≤5时，△BPQ的面积y关于t的函数解析式；‎ ‎（2）求出线段BC、BE、ED的长度；‎ ‎（3）当t为多少秒时，以B、P、Q为顶点的三角形和△ABE相似；‎ ‎（4）如图（3）过E作EF⊥BC于F，△BEF绕点B按顺时针方向旋转一定角度，如果△BEF中E、F的对应点H、I恰好和射线BE、CD的交点G在一条直线，求此时C、I两点之间的距离．‎ ‎13．如图，在△ABC中，以AB为直径的⊙O分别交AC、BC于点D、E，点F在AC的延长线上，且AC=CF，∠CBF=∠CFB．‎ ‎（1）求证：直线BF是⊙O的切线；‎ ‎（2）若点D，点E分别是弧AB的三等分点，当AD=5时，求BF的长；‎ ‎（3）填空：在（2）的条件下，如果以点C为圆心，r为半径的圆上总存在不同的两点到点O的距离为5，则r的取值范围为　　．‎ ‎14．如图，在平面直角坐标系中，点A（，0），B（3，2），C（0，2）．动点D以每秒1个单位的速度从点O出发沿OC向终点C运动，同时动点E以每秒2个单位的速度从点A出发沿AB向终点B运动．过点E作EF⊥AB，交BC于点F，连接DA、DF．设运动时间为t秒．‎ ‎（1）求∠ABC的度数；‎ ‎（2）当t为何值时，AB∥DF；‎ ‎（3）设四边形AEFD的面积为S．①求S关于t的函数关系式；‎ ‎②若一抛物线y=﹣x2+mx经过动点E，当S＜2时，求m的取值范围（写出答案即可）．‎ ‎15．将笔记本电脑放置在水平桌面上，显示屏OB与底板OA夹角为115°（如图1），侧面示意图为图2；使用时为了散热，在底板下面垫入散热架O′AC后，电脑转到AO′B′的位置（如图3），侧面示意图为图4，已知OA=0B=20cm，B′O′⊥OA，垂足为C．‎ ‎（1）求点O′的高度O′C；（精确到0.1cm）‎ ‎（2）显示屏的顶部B′比原来升高了多少？（精确到0.1cm）‎ ‎（3）如图4，要使显示屏O′B′与原来的位置OB平行，显示屏O′B′应绕点O′按顺时针方向旋转多少度？‎ 参考数据：（sin65°=0.906，cos65°=0.423，tan65°=2.146．cot65°=0.446）‎ ‎16．如图，在矩形ABCD中，AB=3，BC=4．动点P从点A出发沿AC向终点C运动，同时动点Q从点B出发沿BA向点A运动，到达A点后立刻以原来的速度沿AB返回．点P，Q运动速度均为每秒1个单位长度，当点P到达点C时停止运动，点Q也同时停止．连结PQ，设运动时间为t（t＞0）秒．‎ ‎（1）在点Q从B到A的运动过程中，‎ ‎①当t=　　时，PQ⊥AC；‎ ‎②求△APQ的面积S关于t的函数关系式，并写出t的取值范围；‎ ‎（2）伴随着P、Q两点的运动，线段PQ的垂直平分线为l．‎ ‎①当l经过点A时，射线QP交AD于点E，求AE的长；‎ ‎②当l经过点B时，求t的值．‎ ‎17．如图1，已知点A（a，0），B（0，b），且a、b满足，▱ABCD的边AD与y轴交于点E，且E为AD中点，双曲线经过C、D两点．‎ ‎（1）求k的值；‎ ‎（2）点P在双曲线上，点Q在y轴上，若以点A、B、P、Q为顶点的四边形是平行四边形，试求满足要求的所有点P、Q的坐标；‎ ‎（3）以线段AB为对角线作正方形AFBH（如图3），点T是边AF上一动点，M是HT的中点，MN⊥HT，交AB于N，当T在AF上运动时，的值是否发生改变？若改变，求出其变化范围；若不改变，请求出其值，并给出你的证明．‎ ‎　‎ 一．选择题（共4小题）‎ ‎1．D；2．D；3．D；4．C；‎ ‎　‎ 二．填空题（共5小题）‎ ‎5．（2n+1﹣2，2n）；6．6：5；7．﹣1；8．或；9．8；‎ ‎　‎ 三．解答题（共8小题）‎ ‎10．；2sinα；11．　　　；12．　　　；13．＜r＜；14．　　　；15．　　　；16．；17．　　　；‎ ‎　‎