2014黑龙江省龙东地区中考数学试题含答案 14页

黑龙江省龙东地区2014年初中毕业学业统一考试 数 学 试 题 本考场试卷序号 ‎（ 由监考填写）‎ 考生注意：‎ ‎1、考试时间120分钟 ‎ ‎2、全卷共三道大题，总分120分 题号 一 二 三 总 分 核分人]‎ ‎21‎ ‎22‎ ‎23‎ ‎24‎ ‎25‎ ‎26‎ ‎27‎ ‎28‎ 得分 得分 评卷人 一、填空题（每题3分，满分30分）‎ A M D B C ‎1. （2014黑龙江省龙东地区，1，3分） 数据显示 ，今年高校毕业生规模达到727万人，比去年有所增加。 数据727万人用科学记数法表示为 人。‎ ‎【答案】7.27×106‎ ‎2. （2014黑龙江省龙东地区，2，3分） 函数中， 自变量的取值范围是 。 ‎ ‎【答案】 x≤3 第3题图 ‎3. （2014黑龙江省龙东地区，3，3分）如图,梯形ABCD中,AD∥BC,点M是AD的中点，不添加辅助线，梯形满足 条件时，有MB＝MC（只填一个即可）。 ‎ ‎【答案】AB=DC(或 ∠ABC=∠DCB、∠A=∠D)等 ‎4. （2014黑龙江省龙东地区，4，3分）三张扑克牌中只有一张黑桃，三位同学依次抽取，第一位同学抽到黑桃的概率为 。‎ ‎【答案】‎ ‎5. （2014黑龙江省龙东地区，5，3分）不等式组2≤3x－7＜8的解集为 。‎ ‎【答案】3≤x＜5 ‎ ‎6. （2014黑龙江省龙东地区，6，3分）直径为10cm的⊙Ｏ中，弦AB＝‎5cm,则弦AB所对的圆周角是 。 ‎ ‎【答案】30°或150°（答对1个给2分，多答或含有错误答案不得分）‎ A B D N M C P ‎7. （2014黑龙江省龙东地区，7，3分）小明带7元钱去买中性笔和橡皮（两种文具都买），中性笔每支2元，橡皮每块1元，那么中性笔能买 支。‎ ‎【答案】1或2或3 （每答对1个给1分，多答或含有错误答案不得分）‎ ‎8. （2014黑龙江省龙东地区，8，3分）△ABC中，AB＝4,BC＝3,∠BAC ‎＝30°,则△ABC的面积为 。 第9题图 ‎【答案】 （答对1个给2分，多答或含有错误答案不得分）‎ ‎9. （2014黑龙江省龙东地区，9，3分）如图，菱形ABCD中，对角线AC=6，BD＝8，M、N分别是BC、CD的中点，P是线段BD上的一个动点，则PM＋PN的最小值是 。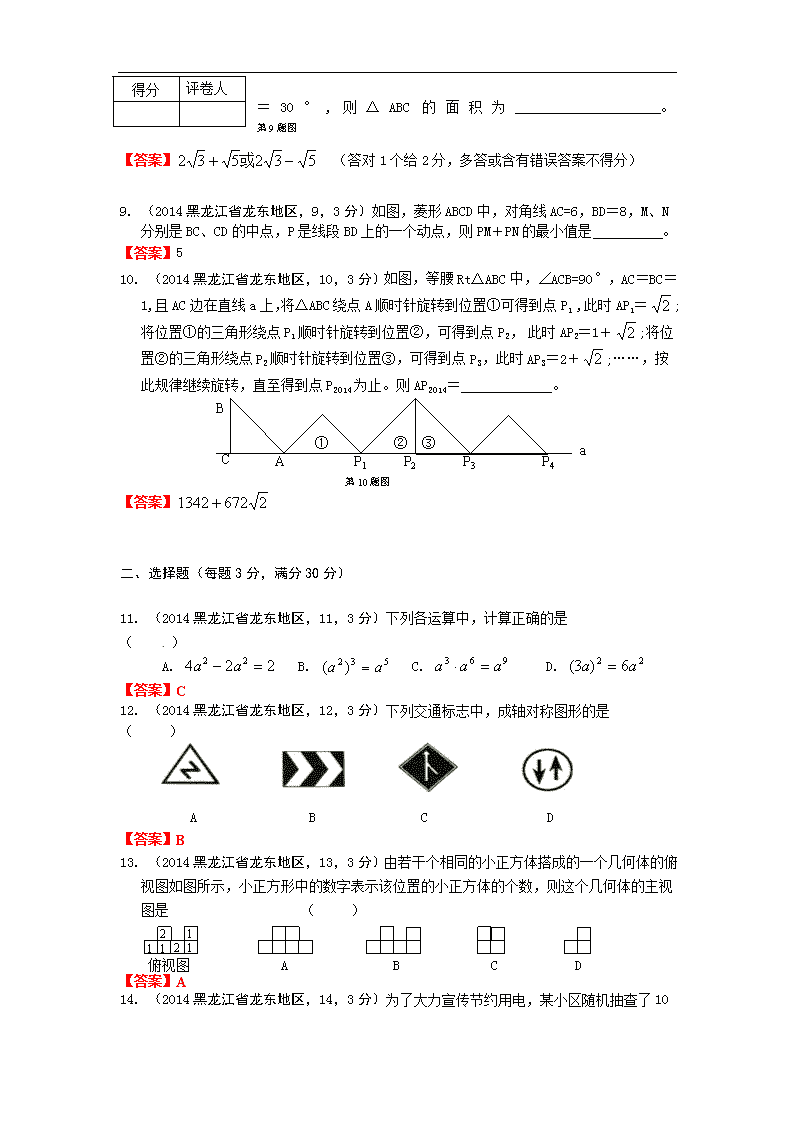‎ ‎【答案】5‎ ‎10. （2014黑龙江省龙东地区，10，3分）如图，等腰Rt△ABC中，∠ACB=90°，AC＝BC＝1,且AC边在直线a上，将△ABC绕点A顺时针旋转到位置①可得到点P1 ,此时AP1＝;将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2， 此时AP2＝1＋;将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3，此时AP3＝2＋;……，按此规律继续旋转，直至得到点P2014为止。则AP2014＝ 。‎ B C A a P1‎ P2‎ P3‎ P4‎ ‎①‎ ‎②‎ ‎③‎ 第10题图 ‎【答案】‎ 得分 评卷人 二、选择题（每题3分，满分30分）‎ ‎11. （2014黑龙江省龙东地区，11，3分）下列各运算中，计算正确的是 （ ）‎ A. B. C. D. ‎ ‎【答案】C ‎12. （2014黑龙江省龙东地区，12，3分）下列交通标志中，成轴对称图形的是 （ ）‎ A B C D ‎【答案】B ‎13. （2014黑龙江省龙东地区，13，3分）由若干个相同的小正方体搭成的一个几何体的俯视图如图所示，小正方形中的数字表示该位置的小正方体的个数，则这个几何体的主视图是 （ ）‎ ‎1‎ ‎1‎ ‎1‎ ‎1‎ ‎2‎ ‎2‎ 俯视图 A B C D ‎【答案】A ‎14. （2014黑龙江省龙东地区，14，3分）为了大力宣传节约用电，某小区随机抽查了 ‎10户家庭的月用电量情况，统计如下表。关于这10户家庭的月用电量说法正确的是 （ ）‎ 月用电量（度）‎ ‎25‎ ‎30‎ ‎40‎ ‎50‎ ‎60‎ 户数 ‎1‎ ‎2‎ ‎4‎ ‎2‎ ‎1‎ A. 中位数是40 B. 众数是4 C. 平均数是20.5 D. 极差是3‎ ‎【答案】A ‎15. （2014黑龙江省龙东地区，15，3分）如图，在平面直角坐标系中，边长为1的正方形ABCD 中，AD边的中点处有一动点P，动点P沿P→D→C→B→A→P运动一周，则P点的纵坐标y与点P走过的路程s之间的函数关系用图象表示大致是 （ ）‎ A D P C BB ‎2‎ ‎1‎ ‎1‎ ‎2‎ ‎0‎ x y ‎2‎ ‎2‎ ‎2‎ ‎2‎ ‎1‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ y s ‎1‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ y s ‎1‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ y s ‎1‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ y s ‎ A B C D ‎【答案】D ‎16. （2014黑龙江省龙东地区，16，3分）已知关于的分式方程的解是非负数，则m的取值范围是 （ ）‎ A. m＞2 B. m≥2 C. m≥2且m≠3 D. m＞2且m≠3‎ ‎【答案】C H F B C E 第18题图 A D ‎17. （2014黑龙江省龙东地区，17，3分）一圆锥体形状的水晶饰品，母线长是10cm，底面圆的直径是5cm，点A为圆锥底面圆周上一点，从A点开始绕圆锥侧面缠一圈彩带回到A点，则彩带最少用多少厘米（接口处重合部分忽略不计） （ ）‎ ‎ A. 10πcm B. 10cm C. 5πcm D. 5cm ‎【答案】B ‎18. （2014黑龙江省龙东地区，18，3分）如图，正方形ABCD的边长为2，H在CD的延长线上，四边形CEFH也为正方形，则△DBF的面积为 （ ）‎ A. 4 B. C. D. 2‎ ‎【答案】D ‎19. （2014黑龙江省龙东地区，19，3分）今年学校举行足球联赛，共赛17轮（即每队均需参赛17场），记分办法是：胜1场得3分，平1场得1分，负1场得0分。在这次足球比赛中，小虎足球队得16分，且踢平场数是所负场数的整数倍，则小虎足球队所负场数的情况有 （ ）‎ A. 2种 B. 3种 C. 4种 D. 5 种 ‎【答案】B 第20题图 A B D C G EA F ‎20. （2014黑龙江省龙东地区，20，3分）如图，正方形 ABCD中，AB＝6，点E在边CD上，‎ 且CD＝3DE。将△ADE沿AE对折至△AFE，延长EF 交边BC于点G,连接AG、CF。则下列结论：‎ ①△ABG≌△AFG ②BG＝CG ③AG∥CF ④S△EGC＝S△AFE ⑤∠AGB＋∠AED＝145°‎ 其中正确的个数是 （ ）‎ A．2 B. 3 C. 4 D. 5‎ ‎【答案】C 三、解答题（满分60分）‎ ‎21. （2014黑龙江省龙东地区，21，5分）‎ 先化简，再求值:，其中 ‎【答案】解：原式=………………………………………1分 ‎ =……………………………………………………………1分 ‎ = …………………………………………………………………1分 当=3时…………………………………………………1分 原式==………………………………………………………………1分 得分 评卷人 ‎22. （2014黑龙江省龙东地区，22，6分）A B C O x y 如图，方格纸中每个小正方形的边长都是1个单位长度， Rt△ABC的三个顶点A（－2，2），B（0，5），C（0，2）。‎ ‎（1） 将△ABC以点C为旋转中心旋转180°，得到△A1B1C， 请画出△A1B1C的图形 。‎ ‎（2）平移△ABC，使点A 的对应点A2坐标为（－2，－6），请画出平移后对应的△A2B2C2的图形。‎ ‎（3）若将△A1B1C绕某一点旋转可得到△A2B2C2，请直接写出旋转中心的坐标。‎ ‎【答案】（1）正确画出旋转后的图形…………………………………………………2分 ‎(2) 正确画出平移后的图形…………………………………………………2分 ‎ （3）旋转中心坐标(0，-2) …………………………………………………2分 得分 评卷人 ‎23. （2014黑龙江省龙东地区，23，6分）‎ 如图, 二次函数的图象与x轴交于A（－3,0）和B（1,0）两点，交y轴于点C（0，3），点C、D是二次函数图象上的一对对称点，一次函数的图象过点B、D。‎ ‎（1）请直接写出D点的坐标。‎ y ‎ x ‎ A ‎ B ‎ C ‎ D ‎ O ‎ ‎（2）求二次函数的解析式。‎ ‎（3）根据图象直接写出使一次函数值大于二次函数值 的x的取值范围。‎ ‎ ‎ 第23题图 ‎【答案】解：（1）D（-2，3）……………………………………………………………1分 ‎（2）设二次函数的解析式为y=ax2+bx+c(a≠0，a、b、c常数)，‎ 根据题意得 ………………………………………………………………1分 ‎9a-3b+c=0‎ a+b+c=0 …………………………………………………………1分 ‎ c=3‎ 解得 a=-1‎ b=-2 …………………………………………………………1分 c=3 ‎ 所以二次函数的解析式为y=-x2－2x+3 …………………………………1分 ‎ (3) x＜-2或x＞1 ………………………………………………………1分 得分 评卷人 ‎60‎ 方式 A B C D E ‎100‎ 人数 ‎0‎ ‎20‎ ‎40‎ ‎80‎ ‎75‎ ‎81‎ ‎90‎ ‎36‎ ‎24.（2014黑龙江省龙东地区，24，6分）‎ 为了更好地宣传“开车不喝酒，‎ 喝酒不开车”的驾车理念，某市 一家报社设计了如下的调查问卷（单选）。在随机调查了 本市全部5000名司机中的部分司机后，整理相关数据并 制作了右侧两个不完整的统计图：‎ 第24题图 A B ‎27%‎ C D E m%‎ 克服酒驾——你认为哪一种方式更好？‎ A．司机酒驾，乘客有责，让乘客帮助监督 B．在车上张贴“请勿喝酒”的提醒标志 C．签订“永不酒驾”保证书 D．希望交警加大检查力度 E．查出酒驾，追究就餐饭店的连带责任 根据以上信息解答下列问题：‎ ‎(1)请补全条形统计图，并直接写出扇形统计图中m= ‎ ‎(2)该市支持选项B的司机大约有多少人？‎ ‎(3)若要从该市支持选项B的司机中随机抽取100名，给他们发放“请勿酒驾”的提醒标志，则支持该选项的司机小李被抽中的概率是多少？‎ ‎【答案】解：（1）补全条形图的高度是18 ……………………………………………2分 计算出m=12 ……………………………………………………………1分 ‎（2）27%×5000=1350（人）………………………………………………2分 ‎（3）小李抽中的概率P==………………………………………2分 得分 评卷人 ‎25．（2014黑龙江省龙东地区，25，8分）一列快车从甲地匀速驶往乙地，一列慢车从乙地匀速驶往甲地，两车同时出发。不久，第二列快车也从甲地发往乙地，速度与第一列快车相同。在第一列快车与慢车相遇30分后，第二列快车与慢车相遇。设慢车行驶的时间为x（单位：时），慢车与第一、第二列快车之间的距离y(单位：千米)与x（单位：时）之间的函数关系如图1、图2所示，根据图象信息解答下列问题：‎ ‎（1）甲、乙两地之间的距离为 千米。‎ ‎（2）求图1中线段CD所表示的y与x之间的函数关系式，并写出自变量x的取值范围。‎ ‎（3）请直接在图2中的（ ）内填上正确的数。‎ y /千米 x /时 图1‎ 图2‎ A ‎900‎ y /千米 a b ‎12‎ ‎( )‎ ‎( )‎ O ‎4.5‎ D B ‎900‎ x /时 ‎4‎ D O ‎12‎ C 第25题图 ‎ ‎ ‎【答案】解：(1) 900 ……………………………………………………………1分 ‎（2）（方法一）慢车速度为900÷12=75千米/时 快车速度+慢车速度=900÷4=225千米/时…………………………1分 快车速度=225-75=150千米/时 快车走完全程时间为900÷150=6小时 快车到达时慢车与快车相距 6×75=450千米 所以C(6，450) ………………………………………………2分 ‎ 设yCD=kx+b（k≠0，k、b为常数）‎ 把（6，450）（12，900）代入yCD=kx+b 中，有 ‎12k+b=900‎ ‎6k+b=450‎ 解得 k=75‎ ‎ b=0 …………………………………………………………1分 所以 y=75x (6≤x≤12)………………………………………………1分 ‎（方法二）设yCD=kx+b（k≠0，k、b为常数）…………………………1分 因为k等于慢车的速度，且慢车速度为900÷12=75千米/时……1分 所以yCD=75x+b ……………………………………………………2分 把D（12，900）代入解析式，有b=0‎ 所以 y=75x (6≤x≤12) ……………………………………………1分 ‎(3) 0.75 (或)………………………………………………1分 ‎ 6.75 （或）……………………………………………1分 得分 评卷人 ‎26．（2014黑龙江省龙东地区，26，8分）已知△ABC中，M为BC的中点，直线m绕点A旋转，过B、M、C分别作BD⊥m于D，ME⊥m于E，CF⊥m于F。‎ ‎（1）当直线m经过B点时，如图1，易证EM＝CF。（不需证明）‎ ‎（D）‎ B F A E M C D B F A E M C D B F A E M C m m m 图1‎ 图2‎ 图3‎ 第26题图 ‎（2）当直线m不经过B点，旋转到如图2、图3的位置时，线段BD、ME、CF之间有怎样的数量关系？请直接写出你的猜想，并选择一种情况加以证明。‎ ‎ ‎ ‎【答案】（2）图2的结论为: ME= (BD+CF)………………………………………2分 图3的结论为: ME= (CF-BD)…………………………………………2分 ‎ 图2的结论证明如下：连接DM并延长交FC的延长线于K ‎ ‎ 又∵BD⊥m,CF⊥m ‎∴BD∥CF ‎∴∠DBM=∠KCM 又∵∠DMB=∠CMK BM=MC ‎∴△DBM≌△KCM…………………………………………………………1分 ‎∴DB=CK DM=MK 由易证知:EM=FK………………………………………………………1分 ‎∴ ME= (CF+CK)= (CF+DB) ………………………………2分 图3的结论证明如下：连接DM并延长交FC于K ‎ ‎ 又∵BD⊥m,CF⊥m ‎∴BD∥CF ‎∴∠MBD=∠KCM 又∵∠DMB=∠CMK BM=MC ‎∴△DBM≌△KCM…………………………………………………………1分 ‎∴DB=CK DM=MK 由易证知:EM=FK…………………………………………………………1分 ‎∴ ME= (CF-CK)= (CF-DB) …………………………………2分 得分 评卷人 ‎27. （2014黑龙江省龙东地区，27，10分）‎ 我市为改善农村生活条件，满足居民清洁能源的需求，计划为万宝村400户居民修建A、B两种型号的沼气池共24个。政府出资36万元，其余资金从各户筹集。两种沼气池的型号、修建费用、可供使用户数、占地面积如下表：‎ 沼气池 修建费用（万元／个）‎ 可供使用户数（户／个）‎ 占地面积（平方米／个）‎ A型 ‎3‎ ‎20‎ ‎10‎ B型 ‎2‎ ‎15‎ ‎8‎ 政府土地部门只批给该村沼气池用地212平方米，设修建A型沼气池x个，修建两种沼气池共需费用y万元。‎ ‎（1）求y与x之间函数关系式。‎ ‎（2）试问有哪几种满足上述要求的修建方案。‎ ‎（3）要想完成这项工程，每户居民平均至少应筹集多少钱？‎ ‎【答案】解：(1) y=3x+2(24-x)=x+48 ………………………………………………2分 ‎ (2) 根据题意得 ‎ 20x+15(24-x) ≥400 ‎ ‎ 10x+8(24-x) ≤212 ……………………… 2分 ‎ ‎ 解得：8≤x≤10 …………………………………………1分 ‎∵x取非负整数 ‎∴ x等于8或9或10 ………………………………………1分 答：有三种满足上述要求的方案：‎ 修建A型沼气池8个，B型沼气池16个 修建A沼气池型9个，B型沼气池15个 ……………………1分 修建A型沼气池10个，B型沼气池14个 ‎（3）y=x+48‎ ‎∵k=1＞0‎ ‎∴ y随x的减小而减小 ‎∴当x=8时，y最小=8+48=56（万元）…………………………………………2分 ‎56－36＝20（万元）‎ ‎200000÷400＝500（元）‎ ‎∴每户至少筹集500元才能完成这项工程中费用最少的方案………………1分 得分 评卷人 ‎28.（2014黑龙江省龙东地区，28，10分）‎ 如图，在平面直角坐标系中，正方形ABCD的顶点A在y轴正半轴上，顶点B在x轴正半轴上，OA、OB的长分别是一元二次方程 x2－7x＋12＝0的两个根（OA＞OB）。‎ ‎（1）求点D的坐标。‎ ‎（2）求直线BC的解析式。‎ ‎ （3）在直线BC上是否存在点P，使△PCD为等腰三角形？若存在，请直接写出点P的坐标；若不存在，说明理由。‎ A B O C D x y 第28题图 第28题图 ‎【答案】解：（1）x2-7x+12=0‎ x1=3,x2=4 ‎ ‎∵OA>OB ‎∴OA=4,OB=3 ……………………………………………………………1分 过D作DE⊥y于点E ‎∵正方形ABCD ‎∴AD=AB ∠DAB=90°‎ ‎∠DAE+∠OAB=90°‎ ‎∠ABO+∠OAB=90°‎ ‎ ∴∠ABO=∠DAE ‎ ∵DE⊥AE ‎∴∠AED =90°=∠AOB ‎∴△DAE≌△ABO …………………………………………………2分 ‎∴DE=OA=4‎ AE=OB=3 OE=7‎ ‎∴D(4,7) ……………………………………………………1分 ‎（2）过点C作CM⊥x轴于点M ‎ 同上可证得△BCM≌△ABO …………………………………………1分 ‎∴CM=OB=3 BM=OA=4 OM=7‎ ‎∴C(7,3) ……………………………………………………1分 设直线BC的解析式为y=kx+b（k≠0，k、b为常数）‎ 代入B(3,0),C(7,3)得 ‎ 7k+b=3 解得 k=‎ ‎ 3k+b=0 b= …………………………………………1分 ‎ ∴y=x ……………………………………………………1分 ‎ (3)存在P1(3,0),P2(11,6)………………………………………………2分 黑龙江省龙东地区2014年初中毕业学业统一考试 ‎ 数学试题参考答案及评分标准 一、填空（每题3分，共30分）‎ ‎1、7.27×106 2、x≤3 3、AB=DC(或 ∠ABC=∠DCB、∠A=∠D)等 4、 ‎ ‎5、3≤x＜5 6、30°或150°（答对1个给2分，多答或含有错误答案不得分）‎ ‎7、1或2或3 （每答对1个给1分，多答或含有错误答案不得分） 8、 （答对1个给2分，多答或含有错误答案不得分）9、5 10、‎ 二、选择题（每题3分，共30分）‎ ‎11、C 12、B 13、A 14、A 15、D 16、C 17、B 18、D 19、B 20、C 三、解答题（满分60分）‎ ‎21、（本题满分5分）‎ 解：原式=………………………………………1分 ‎ =……………………………………………………………1分 ‎ = …………………………………………………………………1分 当=3时…………………………………………………1分 原式==………………………………………………………………1分 ‎22、（本题满分6分）‎ 解：（1）正确画出旋转后的图形…………………………………………………2分 ‎(2) 正确画出平移后的图形…………………………………………………2分 ‎ （3）旋转中心坐标(0，-2) …………………………………………………2分 ‎23、（本题满分6分）‎ 解：（1）D（-2，3）……………………………………………………………1分 ‎（2）设二次函数的解析式为y=ax2+bx+c(a≠0，a、b、c常数)，‎ 根据题意得 ………………………………………………………………1分 ‎9a-3b+c=0‎ a+b+c=0 …………………………………………………………1分 ‎ c=3‎ 解得 a=-1‎ b=-2 …………………………………………………………1分 c=3 ‎ 所以二次函数的解析式为y=-x2－2x+3 …………………………………1分 ‎ (3) x＜-2或x＞1 ………………………………………………………1分 ‎24、（本题满分7分）‎ 解：（1）补全条形图的高度是18 ……………………………………………2分 计算出m=12 ……………………………………………………………1分 ‎（2）27%×5000=1350（人）………………………………………………2分 ‎（3）小李抽中的概率P==………………………………………2分 ‎25、（本题满分8分）‎ 解：(1) 900 ……………………………………………………………1分 ‎（2）（方法一）慢车速度为900÷12=75千米/时 快车速度+慢车速度=900÷4=225千米/时…………………………1分 快车速度=225-75=150千米/时 快车走完全程时间为900÷150=6小时 快车到达时慢车与快车相距 6×75=450千米 所以C(6，450) ………………………………………………2分 ‎ 设yCD=kx+b（k≠0，k、b为常数）‎ 把（6，450）（12，900）代入yCD=kx+b 中，有 ‎12k+b=900‎ ‎6k+b=450‎ 解得 k=75‎ ‎ b=0 …………………………………………………………1分 所以 y=75x (6≤x≤12)………………………………………………1分 ‎（方法二）设yCD=kx+b（k≠0，k、b为常数）…………………………1分 因为k等于慢车的速度，且慢车速度为900÷12=75千米/时……1分 所以yCD=75x+b ……………………………………………………2分 把D（12，900）代入解析式，有b=0‎ 所以 y=75x (6≤x≤12) ……………………………………………1分 ‎(3) 0.75 (或)………………………………………………1分 ‎ 6.75 （或）……………………………………………1分 ‎26、（本题满分8分）‎ ‎（2）图2的结论为: ME= (BD+CF)………………………………………2分 图3的结论为: ME= (CF-BD)…………………………………………2分 ‎ 图2的结论证明如下：连接DM并延长交FC的延长线于K ‎ ‎ 又∵BD⊥m,CF⊥m ‎∴BD∥CF ‎∴∠DBM=∠KCM 又∵∠DMB=∠CMK BM=MC ‎∴△DBM≌△KCM…………………………………………………………1分 ‎∴DB=CK DM=MK 由易证知:EM=FK………………………………………………………1分 ‎∴ ME= (CF+CK)= (CF+DB) ………………………………2分 图3的结论证明如下：连接DM并延长交FC于K ‎ ‎ 又∵BD⊥m,CF⊥m ‎∴BD∥CF ‎∴∠MBD=∠KCM 又∵∠DMB=∠CMK BM=MC ‎∴△DBM≌△KCM…………………………………………………………1分 ‎∴DB=CK DM=MK 由易证知:EM=FK…………………………………………………………1分 ‎∴ ME= (CF-CK)= (CF-DB) …………………………………2分 ‎27、（本题满分10分）‎ 解：(1) y=3x+2(24-x)=x+48 ………………………………………………2分 ‎ (2) 根据题意得 ‎ 20x+15(24-x) ≥400 ‎ ‎ 10x+8(24-x) ≤212 ……………………… 2分 ‎ ‎ 解得：8≤x≤10 …………………………………………1分 ‎∵x取非负整数 ‎∴ x等于8或9或10 ………………………………………1分 答：有三种满足上述要求的方案：‎ 修建A型沼气池8个，B型沼气池16个 修建A沼气池型9个，B型沼气池15个 ……………………1分 修建A型沼气池10个，B型沼气池14个 ‎（3）y=x+48‎ ‎∵k=1＞0‎ ‎∴ y随x的减小而减小 ‎∴当x=8时，y最小=8+48=56（万元）…………………………………………2分 ‎56－36＝20（万元）‎ ‎200000÷400＝500（元）‎ ‎∴每户至少筹集500元才能完成这项工程中费用最少的方案………………1分 ‎ 28、（本题满分10分）‎ 解：（1）x2-7x+12=0‎ x1=3,x2=4 ‎ ‎∵OA>OB ‎∴OA=4,OB=3 ……………………………………………………………1分 过D作DE⊥y于点E ‎∵正方形ABCD ‎∴AD=AB ∠DAB=90°‎ ‎∠DAE+∠OAB=90°‎ ‎∠ABO+∠OAB=90°‎ ‎ ∴∠ABO=∠DAE ‎ ∵DE⊥AE ‎∴∠AED =90°=∠AOB ‎∴△DAE≌△ABO …………………………………………………2分 ‎∴DE=OA=4‎ AE=OB=3 OE=7‎ ‎∴D(4,7) ……………………………………………………1分 ‎（2）过点C作CM⊥x轴于点M ‎ 同上可证得△BCM≌△ABO …………………………………………1分 ‎∴CM=OB=3 BM=OA=4 OM=7‎ ‎∴C(7,3) ……………………………………………………1分 设直线BC的解析式为y=kx+b（k≠0，k、b为常数）‎ 代入B(3,0),C(7,3)得 ‎ 7k+b=3 解得 k=‎ ‎ 3k+b=0 b= …………………………………………1分 ‎ ∴y=x ……………………………………………………1分 ‎ (3)存在P1(3,0),P2(11,6)………………………………………………2分 ‎ 注：本卷中各题若有其它正确的解法，可酌情给分。‎