中考数学压轴题因动点产生的平行四边形问题 5页

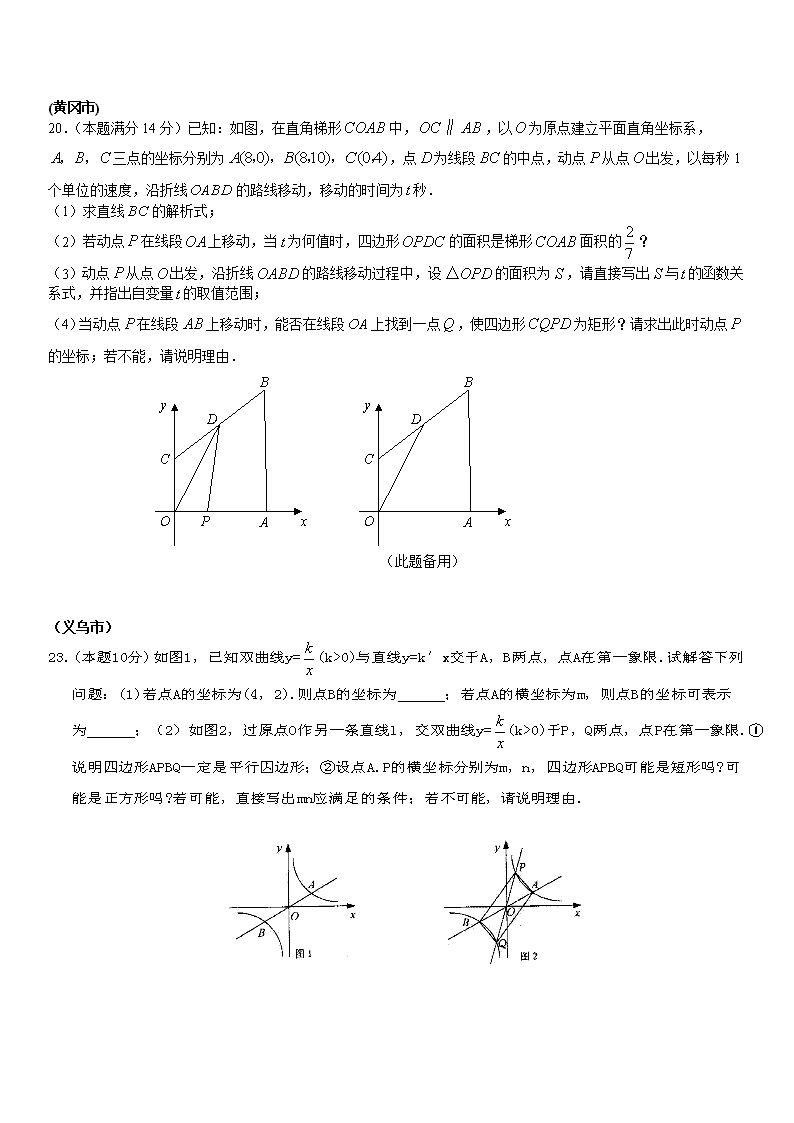
‎(黄冈市)‎ ‎20．（本题满分14分）已知：如图，在直角梯形中，，以为原点建立平面直角坐标系，三点的坐标分别为，点为线段的中点，动点从点出发，以每秒1个单位的速度，沿折线的路线移动，移动的时间为秒．‎ ‎（1）求直线的解析式；‎ ‎（2）若动点在线段上移动，当为何值时，四边形的面积是梯形面积的？‎ ‎（3）动点从点出发，沿折线的路线移动过程中，设的面积为，请直接写出与的函数关系式，并指出自变量的取值范围；‎ ‎（4）当动点在线段上移动时，能否在线段上找到一点，使四边形为矩形？请求出此时动点的坐标；若不能，请说明理由．‎ A B D C O x y ‎（此题备用）‎ A B D C O P x y ‎（义乌市）‎ ‎23. (本题10分) 如图1，已知双曲线y=(k>0)与直线y=k′x交于A，B两点，点A在第一象限.试解答下列问题：(1)若点A的坐标为(4，2).则点B的坐标为 ；若点A的横坐标为m，则点B的坐标可表示为 ；（2）如图2，过原点O作另一条直线l，交双曲线y=(k>0)于P，Q两点，点P在第一象限.①说明四边形APBQ一定是平行囚边形；②设点A.P的横坐标分别为m，n，四边形APBQ可能是短形吗?可能是正方形吗?若可能，直接写出mn应满足的条件；若不可能，请说明理由. 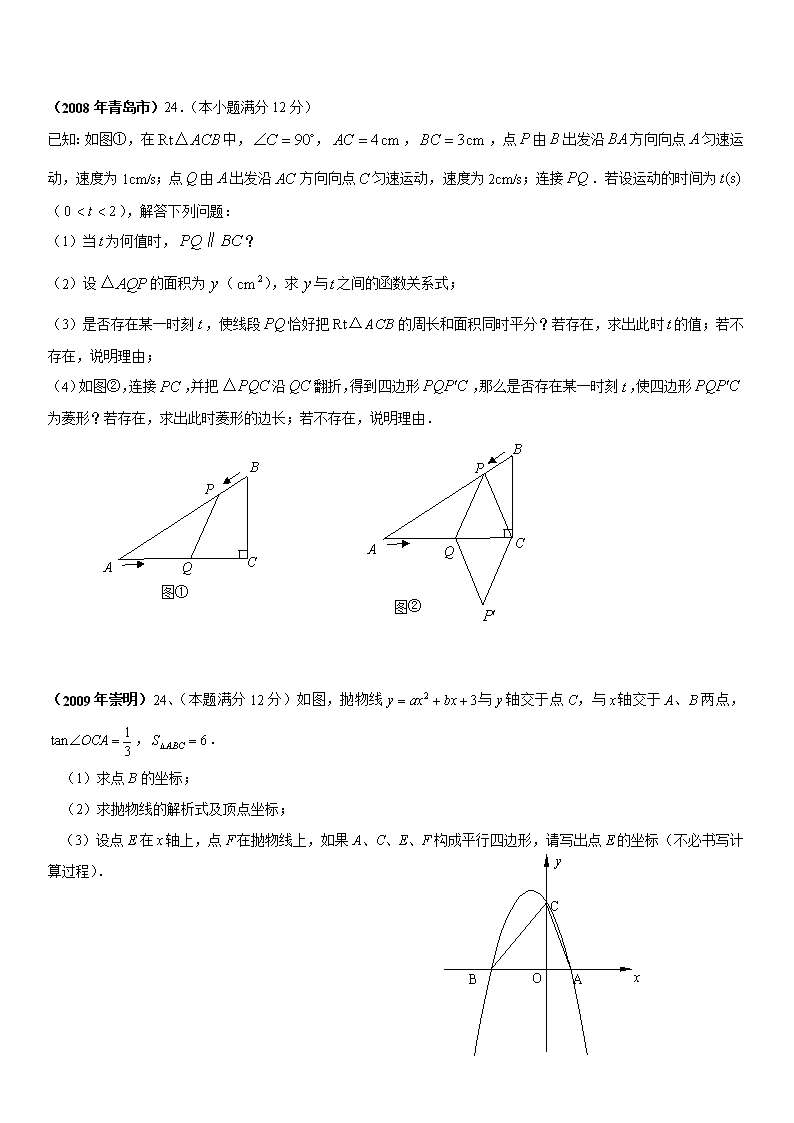‎ ‎（2008年青岛市）24．（本小题满分12分）‎ 已知：如图①，在中，，，，点由出发沿方向向点匀速运动，速度为‎1cm/s；点由出发沿方向向点匀速运动，速度为‎2cm/s；连接．若设运动的时间为（），解答下列问题：‎ ‎（1）当为何值时，？‎ ‎（2）设的面积为（），求与之间的函数关系式；‎ ‎（3）是否存在某一时刻，使线段恰好把的周长和面积同时平分？若存在，求出此时的值；若不存在，说明理由；‎ A Q C P B 图①‎ A Q C P B 图②‎ ‎（4）如图②，连接，并把沿翻折，得到四边形，那么是否存在某一时刻，使四边形为菱形？若存在，求出此时菱形的边长；若不存在，说明理由．‎ ‎（2009年崇明）24、（本题满分12分）如图，抛物线与轴交于点C，与轴交于A、B两点，，．‎ ‎（1）求点B的坐标；‎ ‎（2）求抛物线的解析式及顶点坐标；‎ C A B O y x ‎（3）设点E在轴上，点F在抛物线上，如果A、C、E、F构成平行四边形，请写出点E的坐标（不必书写计算过程）．‎ ‎（2009年普陀区）B C D 第25题 A x y O 25．如图，在平面直角坐标系xOy中，O为原点，‎ 点A、C的坐标分别为（2，0）、（1，）. ‎ 将△AOC绕AC的中点旋转180°，点O落 到点B的位置，抛物线经过 点A，点D是该抛物线的顶点.‎ ‎（1）求证：四边形ABCO是平行四边形；‎ ‎（2）求a的值并说明点B在抛物线上；‎ ‎（3）若点P是线段OA上一点，且∠APD=∠OAB，‎ 求点P的坐标；‎ ‎(4) 若点P是x轴上一点，以P、A、D为顶点作 平行四边形，该平行四边形的另一顶点在y轴 上，写出点P的坐标. ‎ ‎（2009年青浦区）24．（本题满分12分）如图，在平面直角坐标系中，直线分别与轴负半轴交于点A，‎ 与轴的正半轴交于点B，⊙P经过点A、点B（圆心P在轴负半轴上），已知AB=10，.‎ ‎（1）求点P到直线AB的距离；‎ ‎（2）求直线的解析式；‎ y O x B A P ‎（3）在⊙P上是否存在点Q，使以A、P、B、Q为顶点的四边形是菱形？若存在，请求出点Q的坐标；若不存在，请说明理由．‎ ‎（2009年徐汇区）24．（本题满分12分）‎ 如图，抛物线与轴正半轴交于点C，与轴交于点，．‎ ‎（1）求抛物线的解析式； （3分）‎ ‎（2）在直角坐标平面内确定点，使得以点为顶点的四边形是平行四边形，请直接写出点的坐标； （3分）‎ ‎（3）如果⊙过点三点，求圆心的坐标． （6分）‎ A B C O y x ‎（2009年江西省）24．如图，抛物线与轴相交于、两点（点在点的左侧），与轴相交于点，顶点为.‎ ‎（1）直接写出、、三点的坐标和抛物线的对称轴； ‎ ‎（2）连接，与抛物线的对称轴交于点，点为线段上的一个动点，过点作交抛物线于点，设点的横坐标为；‎ x y D C A O B ‎（第24题）‎ ‎①用含的代数式表示线段的长，并求出当为何值时，四边形为平行四边形？‎ ‎②设的面积为，求与的函数关系式.‎ ‎（2009年莆田市）‎