中考数学一模试卷含解析25 23页

‎2016年江苏省扬州市梅岭中学中考数学一模试卷 一、选择题（本大题共有8小题，每小题3分，共24分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）‎ ‎1．下列实数中，是无理数的为（　　）‎ A．0 B．﹣ C． D．3.14‎ ‎2．如图，数轴的单位长度为1，如果点A，B表示的数的绝对值相等，那么点A表示的数是（　　）‎ A．﹣4 B．﹣2 C．0 D．4‎ ‎3．下列四个多项式，能因式分解的是（　　）‎ A．a﹣1 B．a2+1 C．x2﹣4y D．x2﹣6x+9‎ ‎4．下列说法正确的是（　　）‎ A．一个游戏中奖的概率是，则做100次这样的游戏一定会中奖 B．为了了解全国中学生的心理健康状况，应采用普查的方式 C．一组数据0，1，2，1，1的众数和中位数都是1‎ D．若甲组数据的方差S甲2=0.2，乙组数据的方差S乙2=0.5，则乙组数据比甲组数据稳定 ‎5．如图是一个圆柱体，则它的主视图是（　　）‎ A． B． C． D．‎ ‎6．用直尺和圆规作一个角等于已知角，如图，能得出∠A′O′B′=∠AOB的依据是（　　）‎ A．（S、S、S） B．（S、A、S） C．（A、S、A） D．（A、A、S）‎ ‎7．某地下车库出口处安装了“两段式栏杆”，如图1所示，点A是栏杆转动的支点，点E是栏杆两段的联结点．当车辆经过时，栏杆AEF最多只能升起到如图2所示的位置，其示意图如图3所示（栏杆宽度忽略不计），其中AB⊥BC，EF∥BC，∠AEF=143°，AB=AE=1.2米，那么适合该地下车库的车辆限高标志牌为（　　）（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）‎ A． B． C． D．‎ ‎8．如图，在△ABC中，AB=3，AC=2．当∠B最大时，BC的长是（　　）‎ A．1 B． C． D．5‎ ‎　‎ 二、填空题（本大题共有10小题，每小题3分，共30分．不需写出解答过程，请把答案直接填写在答题卡相应位置上）‎ ‎9．2015年扬州市人均GDP超过14000美元，在苏中苏北地区率先超省均．14000用科学记数法表示为______．‎ ‎10．若分式有意义，则x的取值范围为______．‎ ‎11．某校规定：学生的数学学期综合成绩是由平时、期中和期末三项成绩按3：3：4的比例计算所得．若某同学本学期数学的平时、期中和期末成绩分别是90分，90分和85分，则他本学期数学学期综合成绩是______分．‎ ‎12．一个长方形的面积为a3﹣4a，宽为a﹣2，则长为______．‎ ‎13．反比例函数y=与y=2x的图象没有交点，则k的取值范围为______．‎ ‎14．如图，二次函数y=ax2+bx+c的图象经过点（﹣1，0）、（3，0）和（0，2），当x=2时，y的值为______．‎ ‎15．如图，将三角板的直角顶点放在直尺的一边上，若∠1=55°，则∠2的度数为______°．‎ ‎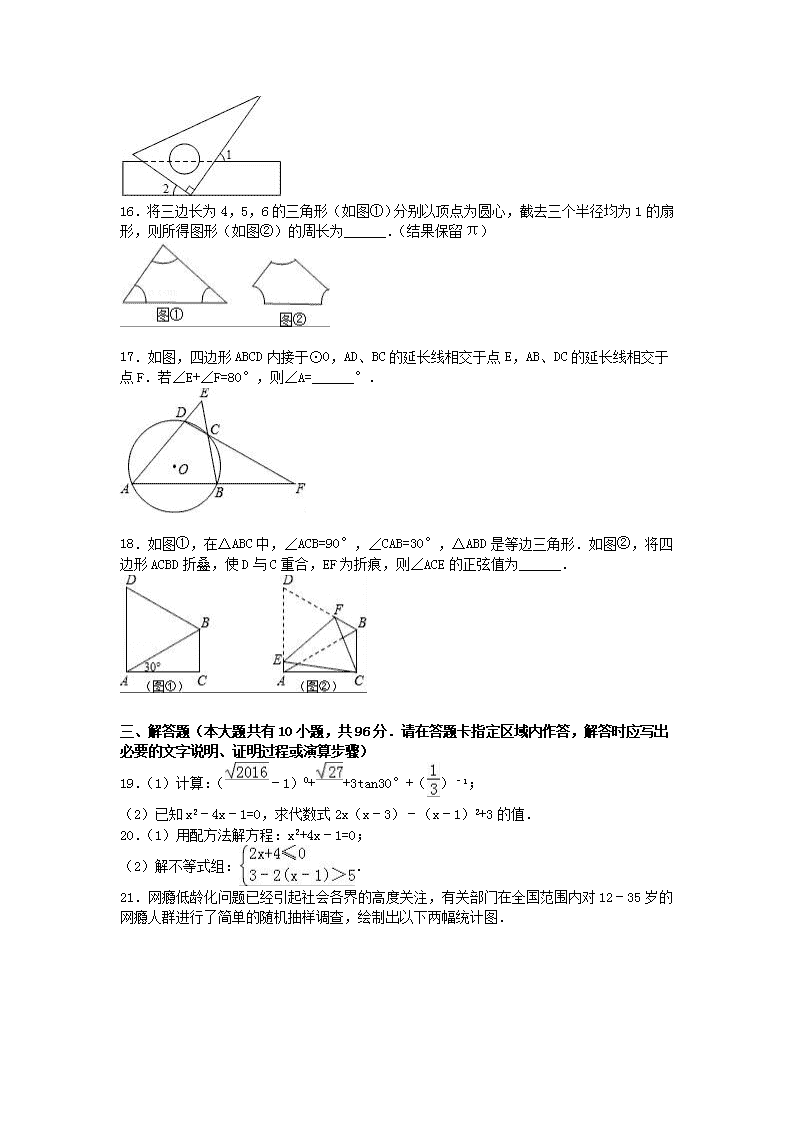16．将三边长为4，5，6的三角形（如图①）分别以顶点为圆心，截去三个半径均为1的扇形，则所得图形（如图②）的周长为______．（结果保留π）‎ ‎17．如图，四边形ABCD内接于⊙O，AD、BC的延长线相交于点E，AB、DC的延长线相交于点F．若∠E+∠F=80°，则∠A=______°．‎ ‎18．如图①，在△ABC中，∠ACB=90°，∠CAB=30°，△ABD是等边三角形．如图②，将四边形ACBD折叠，使D与C重合，EF为折痕，则∠ACE的正弦值为______．‎ ‎　‎ 三、解答题（本大题共有10小题，共96分．请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）‎ ‎19．（1）计算：（﹣1）0++3tan30°+（）﹣1；‎ ‎（2）已知x2﹣4x﹣1=0，求代数式2x（x﹣3）﹣（x﹣1）2+3的值．‎ ‎20．（1）用配方法解方程：x2+4x﹣1=0；‎ ‎（2）解不等式组：．‎ ‎21．网瘾低龄化问题已经引起社会各界的高度关注，有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查，绘制出以下两幅统计图．‎ 请根据图中的信息，回答下列问题：‎ ‎（1）这次抽样调查中共调查了______人；‎ ‎（2）请补全条形统计图；‎ ‎（3）扇形统计图中18﹣23岁部分的圆心角的度数是______；‎ ‎（4）据报道，目前我国12﹣35岁网瘾人数约为2000万，请估计其中12﹣23岁的人数．‎ ‎22．如图，甲、乙用4张扑克牌玩游戏，他俩将扑克牌洗匀后背面朝上，放置在桌面上，每人抽一张，甲先抽，乙后抽，抽出的牌不放回．甲、乙约定：只有甲抽到的牌面数字比乙大时甲胜；否则乙胜．请你用树状图或列表法说明甲、乙获胜的机会是否相同．‎ ‎23．如图，AB=AC，AD=AE，DE=BC，且∠BAD=∠CAE．‎ ‎（1）求证：△ABE≌△ACD；‎ ‎（2）求证：四边形BCDE是矩形．‎ ‎24．为响应市政府“绿色出行”的号召，小张上班由自驾车改为骑公共自行车．已知小张家距上班地点10千米．他骑公共自行车比自驾车平均每小时少行驶45千米，他从家出发到上班地点，骑公共自行车所用的时间是自驾车所用的时间的4倍．小张骑公共自行车平均每小时行驶多少千米？‎ ‎25．如图，△ABC内接于⊙O，且AB=AC，点D在⊙O上，AD⊥AB于点A，AD与BC交于点E，F在DA的延长线上，且AF=AE．‎ ‎（1）求证：BF是⊙O的切线；‎ ‎（2）若AD=4，，求BC的长．‎ ‎26．若y是关于x的函数，H是常数（H＞0），若对于此函数图象上的任意两点（x1，y1），（x2，y2），都有|y1﹣y2|≤H，则称该函数为有界函数，其中满足条件的所有常数H的最小值，称为该函数的界高．如下图所表示的函数的界高为4．‎ ‎（1）若一次函数y=kx+1（﹣2≤x≤1）的界高为4，求k的值；‎ ‎（2）已知m＞﹣2，若函数y=x2（﹣2≤x≤m）的界高为4，求实数m的取值范围．‎ ‎27．已知：l1∥l2∥l3∥l4，平行线l1与l2、l2与l3、l3与l4之间的距离分别为d1、d2、d3，且d1=d3=1，d2=2．我们把四个顶点分别在l1、l2、l3、l4这四条平行线上的四边形称为“格线四边形”．‎ ‎（1）如图1，正方形ABCD为“格线四边形”，则正方形ABCD的边长为______．‎ ‎（2）矩形ABCD为“格线四边形”，其长：宽=2：1，求矩形ABCD的宽．‎ ‎（3）如图1，EG过正方形ABCD的顶点D且垂直l1于点E，分别交l2，l4于点F，G．将∠AEG绕点A顺时针旋转30°得到∠AE′D′（如图2），点D′在直线l3上，以AD′为边在E′D′左侧作菱形AB′C′D′，使B′，C′分别在直线l2，l4上，求菱形AB′C′D′的边长．‎ ‎28．某公司经营杨梅业务，以3万元/吨的价格向农户收购杨梅后，分拣成A、B两类，A类杨梅包装后直接销售；B类杨梅深加工后再销售．A类杨梅的包装成本为1万元/吨，根据市场调查，它的平均销售价格y（单位：万元/吨）与销售数量x（x≥2）之间的函数关系如图；B类杨梅深加工总费用s（单位：万元）与加工数量t（单位：吨）之间的函数关系是s=12+3t，平均销售价格为9万元/吨．‎ ‎（1）直接写出A类杨梅平均销售价格y与销售量x之间的函数关系式；‎ ‎（2）第一次，该公司收购了20吨杨梅，其中A类杨梅有x吨，经营这批杨梅所获得的毛利润为w万元（毛利润=销售总收入﹣经营总成本）．‎ ‎①求w关于x的函数关系式；‎ ‎②若该公司获得了30万元毛利润，问：用于直销的A类杨梅有多少吨？‎ ‎（3）第二次，该公司准备投入132万元资金，请设计一种经营方案，使公司获得最大毛利润，并求出最大毛利润．‎ ‎　‎ ‎2016年江苏省扬州市梅岭中学中考数学一模试卷 参考答案与试题解析 ‎　‎ 一、选择题（本大题共有8小题，每小题3分，共24分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）‎ ‎1．下列实数中，是无理数的为（　　）‎ A．0 B．﹣ C． D．3.14‎ ‎【考点】无理数．‎ ‎【分析】根据无理数是无限不循环小数，可得答案．‎ ‎【解答】解：A、0是有理数，故A错误；‎ B、﹣是有理数，故B错误；‎ C、是无理数，故C正确；‎ D、3.14是有理数，故D错误；‎ 故选：C．‎ ‎　‎ ‎2．如图，数轴的单位长度为1，如果点A，B表示的数的绝对值相等，那么点A表示的数是（　　）‎ A．﹣4 B．﹣2 C．0 D．4‎ ‎【考点】绝对值；数轴．‎ ‎【分析】如果点A，B表示的数的绝对值相等，那么AB的中点即为坐标原点．‎ ‎【解答】解：如图，AB的中点即数轴的原点O．‎ 根据数轴可以得到点A表示的数是﹣2．‎ 故选B．‎ ‎　‎ ‎3．下列四个多项式，能因式分解的是（　　）‎ A．a﹣1 B．a2+1 C．x2﹣4y D．x2﹣6x+9‎ ‎【考点】因式分解-运用公式法；因式分解-提公因式法．‎ ‎【分析】利用平方差公式及完全平方公式的结构特征判断即可．‎ ‎【解答】解：x2﹣6x+9=（x﹣3）2．‎ 故选D．‎ ‎　‎ ‎4．下列说法正确的是（　　）‎ A．一个游戏中奖的概率是，则做100次这样的游戏一定会中奖 B．为了了解全国中学生的心理健康状况，应采用普查的方式 C．一组数据0，1，2，1，1的众数和中位数都是1‎ D．若甲组数据的方差S甲2=0.2，乙组数据的方差S乙2=0.5，则乙组数据比甲组数据稳定 ‎【考点】概率的意义；全面调查与抽样调查；中位数；众数；方差．‎ ‎【分析】根据概率、方差、众数、中位数的定义对各选项进行判断即可．‎ ‎【解答】A、一个游戏中奖的概率是，则做100次这样的游戏有可能中奖一次，该说法错误，故本选项错误；‎ B、为了了解全国中学生的心理健康状况，应采用抽样调查的方式，该说法错误，故本选项错误；‎ C、这组数据的众数是1，中位数是1，故本选项正确；‎ D、方差越大，则平均值的离散程度越大，稳定性也越小，则甲组数据比乙组稳定，故本选项错误；‎ 故选C．‎ ‎　‎ ‎5．如图是一个圆柱体，则它的主视图是（　　）‎ A． B． C． D．‎ ‎【考点】简单几何体的三视图．‎ ‎【分析】找到从物体的正面看，所得到的图形即可．‎ ‎【解答】解：一个直立在水平面上的圆柱体的主视图是长方形，‎ 故选A ‎　‎ ‎6．用直尺和圆规作一个角等于已知角，如图，能得出∠A′O′B′=∠AOB的依据是（　　）‎ A．（S、S、S） B．（S、A、S） C．（A、S、A） D．（A、A、S）‎ ‎【考点】全等三角形的判定与性质；作图—基本作图．‎ ‎【分析】利用SSS可证得△OCD≌△O′C′D′，那么∠A′O′B′=∠AOB．‎ ‎【解答】解：易得OC=0′C'，OD=O′D'，CD=C′D'，那么△OCD≌△O′C′D′，‎ 可得∠A′O′B′=∠AOB，所以利用的条件为SSS，‎ 故选A．‎ ‎　‎ ‎7．某地下车库出口处安装了“两段式栏杆”，如图1所示，点A是栏杆转动的支点，点E是栏杆两段的联结点．当车辆经过时，栏杆AEF最多只能升起到如图2所示的位置，其示意图如图3所示（栏杆宽度忽略不计），其中AB⊥BC，EF∥BC，∠AEF=143°，AB=AE=1.2米，那么适合该地下车库的车辆限高标志牌为（　　）（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）‎ A． B． C． D．‎ ‎【考点】解直角三角形的应用．‎ ‎【分析】过点A作BC的平行线AG，过点E作EH⊥AG于H，则∠BAG=90°，∠EHA=90°．先求出∠AEH=53°，则∠EAH=37°，然后在△EAH中，利用正弦函数的定义得出EH=AE•sin∠EAH，则栏杆EF段距离地面的高度为：AB+EH，代入数值计算即可．‎ ‎【解答】解：如图，过点A作BC的平行线AG，过点E作EH⊥AG于H，‎ 则∠EHG=∠HEF=90°，‎ ‎∵∠AEF=143°，‎ ‎∴∠AEH=∠AEF﹣∠HEF=53°，‎ ‎∠EAH=37°，‎ 在△EAH中，∠EHA=90°，∠EAH=37°，AE=1.2米，‎ ‎∴EH=AE•sin∠EAH≈1.2×0.60=0.72（米），‎ ‎∵AB=1.2米，‎ ‎∴AB+EH≈1.2+0.72=1.92≈1.9米．‎ 故选：A．‎ ‎　‎ ‎8．如图，在△ABC中，AB=3，AC=2．当∠B最大时，BC的长是（　　）‎ A．1 B． C． D．5‎ ‎【考点】切线的性质；勾股定理．‎ ‎【分析】以AC为直径作⊙O，当BC为⊙O的切线时，即BC⊥AC时，∠B最大，根据勾股定理即可求出答案．‎ ‎【解答】解：以AC为直径作⊙O，当BC为⊙O的切线时，即BC⊥AC时，∠B最大，‎ 此时BC===．‎ 故选B．‎ ‎　‎ 二、填空题（本大题共有10小题，每小题3分，共30分．不需写出解答过程，请把答案直接填写在答题卡相应位置上）‎ ‎9．2015年扬州市人均GDP超过14000美元，在苏中苏北地区率先超省均．14000用科学记数法表示为　1.4×104　．‎ ‎【考点】科学记数法—表示较大的数．‎ ‎【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．‎ ‎【解答】解：14000用科学记数法表示为1.4×104，‎ 故答案为：1.4×104．‎ ‎　‎ ‎10．若分式有意义，则x的取值范围为　x≠2　．‎ ‎【考点】分式有意义的条件．‎ ‎【分析】根据分母不为零分式有意义，可得答案．‎ ‎【解答】解：由题意，得 x﹣2≠0．‎ 解得x≠2，‎ 故答案为：x≠2．‎ ‎　‎ ‎11．某校规定：学生的数学学期综合成绩是由平时、期中和期末三项成绩按3：3：4的比例计算所得．若某同学本学期数学的平时、期中和期末成绩分别是90分，90分和85分，则他本学期数学学期综合成绩是　88　分．‎ ‎【考点】加权平均数．‎ ‎【分析】按3：3：4的比例算出本学期数学学期综合成绩即可．‎ ‎【解答】解：本学期数学学期综合成绩=90×30%+90×30%+85×40%=88（分）．‎ 故答案为：88．‎ ‎　‎ ‎12．一个长方形的面积为a3﹣4a，宽为a﹣2，则长为　a（a+2）　．‎ ‎【考点】整式的除法．‎ ‎【分析】由长方形面积除以宽求出长即可．‎ ‎【解答】解：根据题意得：（a3﹣4a）÷（a﹣2）=a（a+2）（a﹣2）÷（a﹣2）=a（a+2），‎ 故答案为：a（a+2）‎ ‎　‎ ‎13．反比例函数y=与y=2x的图象没有交点，则k的取值范围为　k＞1　．‎ ‎【考点】反比例函数与一次函数的交点问题．‎ ‎【分析】根据反比例函数与一次函数图象的特征，得到1﹣k小于0，即可确定出k的范围．‎ ‎【解答】解：∵函数y=与y=2x的图象没有交点，‎ ‎∴1﹣k＜0，即k＞1，‎ 故答案为：k＞1．‎ ‎　‎ ‎14．如图，二次函数y=ax2+bx+c的图象经过点（﹣1，0）、（3，0）和（0，2），当x=2时，y的值为　2　．‎ ‎【考点】待定系数法求二次函数解析式．‎ ‎【分析】把三点坐标代入二次函数解析式求出a，b，c的值，即可确定出二次函数解析式，然后把x=2代入解析式即可求得．‎ ‎【解答】解：∵二次函数y=ax2+bx+c的图象经过点（﹣1，0）、（3，0）和（0，2），‎ ‎∴，‎ 解得：，‎ 则这个二次函数的表达式为y=﹣x2+x+2．‎ 把x=2代入得，y=﹣×4+×2+2=2．‎ 故答案为2．‎ ‎　‎ ‎15．如图，将三角板的直角顶点放在直尺的一边上，若∠1=55°，则∠2的度数为　35　°．‎ ‎【考点】平行线的性质；余角和补角．‎ ‎【分析】根据平角等于180°求出∠3，再根据两直线平行，同位角相等可得∠2+90°=∠3．‎ ‎【解答】解：如图：‎ ‎∵∠3=180°﹣∠1=180°﹣55°=125°，‎ ‎∵直尺两边互相平行，‎ ‎∴∠2+90°=∠3，‎ ‎∴∠2=125°﹣90°=35°．‎ 故答案为：35．‎ ‎　‎ ‎16．将三边长为4，5，6的三角形（如图①）分别以顶点为圆心，截去三个半径均为1的扇形，则所得图形（如图②）的周长为　9+π　．（结果保留π）‎ ‎【考点】弧长的计算；三角形内角和定理．‎ ‎【分析】先计算三段弧的长度，再用三角形的周长减去6，把结果加起来即可得到答案．‎ ‎【解答】解：三段弧的长度==π，‎ 三角形的周长=4+5+6=15，‎ 图②的周长=π+15﹣6=9+π，‎ 故答案为9+π．‎ ‎　‎ ‎17．如图，四边形ABCD内接于⊙O，AD、BC的延长线相交于点E，AB、DC的延长线相交于点F．若∠E+∠F=80°，则∠A=　50　°．‎ ‎【考点】圆内接四边形的性质．‎ ‎【分析】连结EF，如图，根据圆内接四边形的性质得∠A+∠BCD=180°，根据对顶角相等得∠BCD=∠ECF，则∠A+∠ECF=180°，根据三角形内角和定理得∠ECF+∠1+∠2=180°，所以∠1+∠2=∠A，再利用三角形内角和定理得到∠A+∠AEB+∠1+∠2+∠AFD=180°，则∠A+80°+∠A=180°，然后解方程即可．‎ ‎【解答】解：连结EF，如图，‎ ‎∵四边形ABCD内接于⊙O，‎ ‎∴∠A+∠BCD=180°，‎ 而∠BCD=∠ECF，‎ ‎∴∠A+∠ECF=180°，‎ ‎∵∠ECF+∠1+∠2=180°，‎ ‎∴∠1+∠2=∠A，‎ ‎∵∠A+∠AEF+∠AFE=180°，‎ 即∠A+∠AEB+∠1+∠2+∠AFD=180°，‎ ‎∴∠A+80°+∠A=180°，‎ ‎∴∠A=50°．‎ 故答案为：50．‎ ‎　‎ ‎18．如图①，在△ABC中，∠ACB=90°，∠CAB=30°，△ABD是等边三角形．如图②，将四边形ACBD折叠，使D与C重合，EF为折痕，则∠ACE的正弦值为　　．‎ ‎【考点】翻折变换（折叠问题）；含30度角的直角三角形；解直角三角形．‎ ‎【分析】在Rt△ABC中，设AB=2a，已知∠ACB=90°，∠CAB=30°，即可求得AB、AC的值，由折叠的性质知：DE=CE，可设出DE、CE的长，然后表示出AE的长，进而可在Rt△AEC中，由勾股定理求得AE、CE的值，即可求∠ACE的正弦值．‎ ‎【解答】解：∵△ABC中，∠ACB=90°，∠BAC=30°，设AB=2a，‎ ‎∴AC=a，BC=a；‎ ‎∵△ABD是等边三角形，‎ ‎∴AD=AB=2a；‎ 设DE=EC=x，则AE=2a﹣x；‎ 在Rt△AEC中，由勾股定理，得：（2a﹣x）2+3a2=x2，‎ 解得：x=a；‎ ‎∴AE=a，EC=a，‎ ‎∴sin∠ACE==；‎ 故答案为：．‎ ‎　‎ 三、解答题（本大题共有10小题，共96分．请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）‎ ‎19．（1）计算：（﹣1）0++3tan30°+（）﹣1；‎ ‎（2）已知x2﹣4x﹣1=0，求代数式2x（x﹣3）﹣（x﹣1）2+3的值．‎ ‎【考点】整式的混合运算—化简求值；实数的运算；零指数幂；负整数指数幂；特殊角的三角函数值．‎ ‎【分析】（1）根据零指数幂、特殊角的三角函数值、负整数指数幂可以解答本题；‎ ‎（2）先对原式化简建立与x2﹣4x﹣1=0的关系，从而可以解答本题．‎ ‎【解答】解：（1）（﹣1）0++3tan30°+（）﹣1‎ ‎=1+3+3×+3‎ ‎=1+3++3‎ ‎=4+4；‎ ‎（2）∵x2﹣4x﹣1=0，‎ ‎∴x2﹣4x=1，‎ ‎∴2x（x﹣3）﹣（x﹣1）2+3‎ ‎=2x2﹣6x﹣x2+2x﹣1+3‎ ‎=x2﹣4x+2‎ ‎=1+2‎ ‎=3．‎ ‎　‎ ‎20．（1）用配方法解方程：x2+4x﹣1=0；‎ ‎（2）解不等式组：．‎ ‎【考点】解一元二次方程-配方法；解一元一次不等式组．‎ ‎【分析】（1）先移项，再配方，最后直接开平方即可；‎ ‎（2）先解两个不等式，再求不等式解集的公共部分即可．‎ ‎【解答】解：（1）移项得，x2+4x=1，‎ 配方得，x2+4x+4=5，‎ 即（x+2）2=5，‎ ‎∴x+2=±，‎ ‎∴x1=﹣2+，x2=﹣2﹣；‎ ‎（2）由①得：x≤﹣2，‎ ‎ 由②得：x＜0，‎ ‎∴不等式组的解集为x≤﹣2．‎ ‎　‎ ‎21．网瘾低龄化问题已经引起社会各界的高度关注，有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查，绘制出以下两幅统计图．‎ 请根据图中的信息，回答下列问题：‎ ‎（1）这次抽样调查中共调查了　1500　人；‎ ‎（2）请补全条形统计图；‎ ‎（3）扇形统计图中18﹣23岁部分的圆心角的度数是　108°　；‎ ‎（4）据报道，目前我国12﹣35岁网瘾人数约为2000万，请估计其中12﹣23岁的人数．‎ ‎【考点】条形统计图；用样本估计总体；扇形统计图．‎ ‎【分析】（1）根据30﹣35岁的人数除以所占的百分比，可得调查的人数；‎ ‎（2）根据有理数的减法，可得12﹣17岁的人数，根据12﹣17岁的人数，可得答案；‎ ‎（3）根据18﹣23岁的人数除以抽查的人数乘以360°，可得答案；‎ ‎（4）根据总人数乘以12﹣23岁的人数所占的百分比，可得答案．‎ ‎【解答】解：（1）这次抽样调查中共调查了330÷22%=1500（人）；‎ ‎（2）12﹣17岁的人数为1500﹣450﹣420﹣330=300（人）‎ 补充完整，如图；‎ ‎（3）扇形统计图中18﹣23岁部分的圆心角的度数是×360°=108°；‎ ‎（4）其中12﹣23岁的人数 2000×50%=1000（万人）．‎ ‎　‎ ‎22．如图，甲、乙用4张扑克牌玩游戏，他俩将扑克牌洗匀后背面朝上，放置在桌面上，每人抽一张，甲先抽，乙后抽，抽出的牌不放回．甲、乙约定：只有甲抽到的牌面数字比乙大时甲胜；否则乙胜．请你用树状图或列表法说明甲、乙获胜的机会是否相同．‎ ‎【考点】列表法与树状图法．‎ ‎【分析】首先根据题意画出树状图，然后由树状图求得所有等可能的结果与甲胜、乙胜的情况，然后利用概率公式求解即可求得答案．‎ ‎【解答】解：画树状图得：‎ ‎∵共有12种等可能的结果，甲抽到的牌面数字比乙大的有5种情况，小于等于乙的有7种情况，‎ ‎∴P（甲胜）=，P（乙胜）=，‎ ‎∴甲、乙获胜的机会不相同．‎ ‎　‎ ‎23．如图，AB=AC，AD=AE，DE=BC，且∠BAD=∠CAE．‎ ‎（1）求证：△ABE≌△ACD；‎ ‎（2）求证：四边形BCDE是矩形．‎ ‎【考点】矩形的判定；全等三角形的判定与性质．‎ ‎【分析】（1）利用SAS证得两个三角形全等即可；‎ ‎（2）要证明四边形BCED为矩形，则要证明四边形BCED是平行四边形，且对角线相等．‎ ‎【解答】（1）证明：∵∠BAD=∠CAE，‎ ‎∴∠EAB=∠DAC，‎ 在△ABE和△ACD中 ‎∵AB=AC，∠EAB=∠DAC，AE=AD ‎∴△ABE≌△ACD（SAS）；‎ ‎（2）∵△ABE≌△ACD，‎ ‎∴BE=CD，‎ 又DE=BC，‎ ‎∴四边形BCDE为平行四边形．‎ ‎∵AB=AC，‎ ‎∴∠ABC=∠ACB ‎∵△ABE≌△ACD，‎ ‎∴∠ABE=∠ACD，‎ ‎∴∠EBC=∠DCB ‎∵四边形BCDE为平行四边形，‎ ‎∴EB∥DC，‎ ‎∴∠EBC+∠DCB=180°，‎ ‎∴∠EBC=∠DCB=90°，‎ 四边形BCDE是矩形．‎ ‎　‎ ‎24．为响应市政府“绿色出行”的号召，小张上班由自驾车改为骑公共自行车．已知小张家距上班地点10千米．他骑公共自行车比自驾车平均每小时少行驶45千米，他从家出发到上班地点，骑公共自行车所用的时间是自驾车所用的时间的4倍．小张骑公共自行车平均每小时行驶多少千米？‎ ‎【考点】分式方程的应用．‎ ‎【分析】设小张骑公共自行车上班平均每小时行驶x千米，根据骑公共自行车所用的时间是自驾车所用的时间的4倍列出方程，求解即可．‎ ‎【解答】解：设小张骑公共自行车上班平均每小时行驶x千米，则骑自驾车平均每小时行驶（x+45）千米．‎ 根据题意列方程得： =4×，‎ 解得：x=15，‎ 经检验，x=15是原方程的解，且符合实际意义．‎ 答：小张用骑公共自行车方式上班平均每小时行驶15千米．‎ ‎　‎ ‎25．如图，△ABC内接于⊙O，且AB=AC，点D在⊙O上，AD⊥AB于点A，AD与BC交于点E，F在DA的延长线上，且AF=AE．‎ ‎（1）求证：BF是⊙O的切线；‎ ‎（2）若AD=4，，求BC的长．‎ ‎【考点】切线的判定；解直角三角形．‎ ‎【分析】（1）连接BD，因AD⊥AB，所以BD是直径．证明BF⊥DB即可．‎ ‎（2）作AG⊥BC于点G．由（1）中结论∠D=∠2=∠3，分别把这三个角转化到直角三角形中，根据，求相关线段的长．‎ ‎【解答】证明：（1）如图，连接BD．‎ ‎∵AD⊥AB，D在圆O上，‎ ‎∴∠DAB=90°，‎ ‎∴DB是⊙O的直径．‎ ‎∴∠1+∠2+∠D=90°．‎ 又∵AE=AF，‎ ‎∴BE=BF，∠2=∠3．‎ ‎∵AB=AC，‎ ‎∴∠D=∠C=∠2=∠3．‎ ‎∴∠1+∠2+∠3=90°．‎ 即OB⊥BF于B．‎ ‎∴直线BF是⊙O的切线． ‎ ‎（2）作AG⊥BC于点G．‎ ‎∵∠D=∠2=∠3，‎ ‎∴．‎ 在Rt△ABD中，∠DAB=90°，AD=4，，‎ ‎∴，．‎ 在Rt△ABG中，∠AGB=90°，AB=3，，‎ ‎∴．‎ ‎∵AB=AC，‎ ‎∴． ‎ ‎　‎ ‎26．若y是关于x的函数，H是常数（H＞0），若对于此函数图象上的任意两点（x1，y1），（x2，y2），都有|y1﹣y2|≤H，则称该函数为有界函数，其中满足条件的所有常数H的最小值，称为该函数的界高．如下图所表示的函数的界高为4．‎ ‎（1）若一次函数y=kx+1（﹣2≤x≤1）的界高为4，求k的值；‎ ‎（2）已知m＞﹣2，若函数y=x2（﹣2≤x≤m）的界高为4，求实数m的取值范围．‎ ‎【考点】二次函数的性质；一次函数的性质．‎ ‎【分析】（1）根据界高的定义，列出绝对值方程即可解决问题．‎ ‎（2）根据界高的定义，列出绝对值方程即可解决问题．‎ ‎【解答】解：（1）由题意：|﹣2k+1﹣（k+1）|=4，‎ ‎∴|﹣3k|=4，‎ ‎∴k=．‎ ‎（2）由题意：|4﹣m2|=4，‎ m=0或2，‎ ‎∴O≤m．‎ ‎　‎ ‎27．已知：l1∥l2∥l3∥l4，平行线l1与l2、l2与l3、l3与l4之间的距离分别为d1、d2、d3，且d1=d3=1，d2=2．我们把四个顶点分别在l1、l2、l3、l4这四条平行线上的四边形称为“格线四边形”．‎ ‎（1）如图1，正方形ABCD为“格线四边形”，则正方形ABCD的边长为　　．‎ ‎（2）矩形ABCD为“格线四边形”，其长：宽=2：1，求矩形ABCD的宽．‎ ‎（3）如图1，EG过正方形ABCD的顶点D且垂直l1于点E，分别交l2，l4于点F，G．将∠AEG绕点A顺时针旋转30°得到∠AE′D′（如图2），点D′在直线l3上，以AD′为边在E′D′左侧作菱形AB′C′D′，使B′，C′分别在直线l2，l4上，求菱形AB′C′D′的边长．‎ ‎【考点】四边形综合题．‎ ‎【分析】（1）利用已知得出△AED≌△DGC（AAS），即可得出AE，以及正方形的边长；‎ ‎（2）如图2过点B作BE⊥L1于点E，反向延长BE交L4于点F，则BE=1，BF=3，由四边形ABCD是矩形，∠ABC=90°，∠ABE+∠FBC=90°，根据∠ABE+∠EAB=90°，得到∠FBC=∠EAB，然后分类讨论，求得矩形的宽．‎ ‎（3）首先过点E′作ON垂直于l1分别交l1，l2于点O，N，∠AEO=30°，则∠ED′N=60°，可求出AE=1，EO，EN，ED′的长，进而由勾股定理可知菱形的边长．‎ ‎【解答】解：（1）∵l1∥l2∥l3∥l4，∠AED=90°‎ ‎∴∠DGC=90°，‎ ‎∵四边形ABCD为正方形 ‎∴∠ADC=90°，AD=CD，∵∠ADE+∠2=90°，‎ ‎∴∠1+∠2=90°，‎ ‎∴∠1=∠ADE，‎ ‎∵l3∥l4‎ ‎∴∠1=∠DCG，‎ ‎∠ADE=∠DCG，‎ 在△AED与△DGC中，‎ ‎，‎ ‎∴△AED≌△GDC（AAS），‎ ‎∴AE=GD=1，ED=GC=3，‎ ‎∴AD==，‎ 故答案为：；‎ ‎（2）如图2过点B作BE⊥L1于点E，反向延长BE交L4于点F，‎ 则BE=1，BF=3，‎ ‎∵四边形ABCD是矩形，‎ ‎∴∠ABC=90°，‎ ‎∴∠ABE+∠FBC=90°，‎ ‎∵∠ABE+∠EAB=90°，‎ ‎∴∠FBC=∠EAB，‎ 当AB＜BC时，AB=BC，‎ ‎∴AE=BF=，‎ ‎∴AB==；‎ 如图3当AB＞BC时，‎ 同理可得：BC=，‎ ‎∴矩形的宽为：，；‎ ‎（3）如图4过点E′作ON垂直于l1分别交l1，l4于点O，N，‎ ‎∵∠OAE′=30°，则∠E′FN=60°‎ ‎∵AE′=AE=1，‎ 故E′O=，E′N=，E′D′=，‎ 由勾股定理可知菱形的边长为： ==．‎ ‎　‎ ‎28．某公司经营杨梅业务，以3万元/吨的价格向农户收购杨梅后，分拣成A、B两类，A类杨梅包装后直接销售；B类杨梅深加工后再销售．A类杨梅的包装成本为1万元/吨，根据市场调查，它的平均销售价格y（单位：万元/吨）与销售数量x（x≥2）之间的函数关系如图；B类杨梅深加工总费用s（单位：万元）与加工数量t（单位：吨）之间的函数关系是s=12+3t，平均销售价格为9万元/吨．‎ ‎（1）直接写出A类杨梅平均销售价格y与销售量x之间的函数关系式；‎ ‎（2）第一次，该公司收购了20吨杨梅，其中A类杨梅有x吨，经营这批杨梅所获得的毛利润为w万元（毛利润=销售总收入﹣经营总成本）．‎ ‎①求w关于x的函数关系式；‎ ‎②若该公司获得了30万元毛利润，问：用于直销的A类杨梅有多少吨？‎ ‎（3）第二次，该公司准备投入132万元资金，请设计一种经营方案，使公司获得最大毛利润，并求出最大毛利润．‎ ‎【考点】二次函数的应用．‎ ‎【分析】（1）这是一个分段函数，分别求出其函数关系式；‎ ‎（2）①当2≤x＜8时及当x≥8时，分别求出w关于x的表达式．注意w=销售总收入﹣经营总成本=wA+wB﹣3×20；‎ ‎②若该公司获得了30万元毛利润，将30万元代入①中求得的表达式，求出A类杨梅的数量；‎ ‎（3）本问是方案设计问题，总投入为132万元，这笔132万元包括购买杨梅的费用+A类杨梅加工成本+‎ B类杨梅加工成本．共购买了m吨杨梅，其中A类杨梅为x吨，B类杨梅为（m﹣x）吨，分别求出当2≤x＜8时及当x≥8时w关于x的表达式，并分别求出其最大值．‎ ‎【解答】解：（1）①当2≤x＜8时，如图，‎ 设直线AB解析式为：y=kx+b，‎ 将A（2，12）、B（8，6）代入得：‎ ‎，解得，‎ ‎∴y=﹣x+14；‎ ‎②当x≥8时，y=6．‎ 所以A类杨梅平均销售价格y与销售量x之间的函数关系式为：‎ y=；‎ ‎（2）设销售A类杨梅x吨，则销售B类杨梅（20﹣x）吨．‎ ‎①当2≤x＜8时，‎ wA=x（﹣x+14）﹣x=﹣x2+13x；‎ wB=9（20﹣x）﹣[12+3（20﹣x）]=108﹣6x ‎∴w=wA+wB﹣3×20‎ ‎=（﹣x2+13x）+﹣60‎ ‎=﹣x2+7x+48；‎ 当x≥8时，‎ wA=6x﹣x=5x；‎ wB=9（20﹣x）﹣[12+3（20﹣x）]=108﹣6x ‎∴w=wA+wB﹣3×20‎ ‎=（5x）+﹣60‎ ‎=﹣x+48．‎ ‎∴w关于x的函数关系式为：‎ w=．‎ ‎②当2≤x＜8时，﹣x2+7x+48=30，解得x1=9，x2=﹣2，均不合题意；‎ 当x≥8时，﹣x+48=30，解得x=18．‎ ‎∴当毛利润达到30万元时，直接销售的A类杨梅有18吨．‎ ‎（3）设该公司用132万元共购买了m吨杨梅，其中A类杨梅为x吨，B类杨梅为（m﹣x）吨，‎ 则购买费用为3m万元，A类杨梅加工成本为x万元，B类杨梅加工成本为[12+3（m﹣x）]万元，‎ ‎∴3m+x+[12+3（m﹣x）]=132，化简得：x=3m﹣60．‎ ‎①当2≤x＜8时，‎ wA=x（﹣x+14）﹣x=﹣x2+13x；‎ wB=9（m﹣x）﹣[12+3（m﹣x）]=6m﹣6x﹣12‎ ‎∴w=wA+wB﹣3×m ‎=（﹣x2+13x）+（6m﹣6x﹣12）﹣3m ‎=﹣x2+7x+3m﹣12．‎ 将3m=x+60代入得：w=﹣x2+8x+48=﹣（x﹣4）2+64‎ ‎∴当x=4时，有最大毛利润64万元，‎ 此时m=，m﹣x=；‎ ‎②当x≥8时，‎ wA=6x﹣x=5x；‎ wB=9（m﹣x）﹣[12+3（m﹣x）]=6m﹣6x﹣12‎ ‎∴w=wA+wB﹣3×m ‎=（5x）+（6m﹣6x﹣12）﹣3m ‎=﹣x+3m﹣12．‎ 将3m=x+60代入得：w=48‎ ‎∴当x＞8时，有最大毛利润48万元．‎ 综上所述，购买杨梅共吨，其中A类杨梅4吨，B类吨，公司能够获得最大毛利润，最大毛利润为64万元．‎