上海市浦东新区中考数学一模及答案 10页

浦东新区2017学年第一学期初三教学质量检测 数 学 试 卷 ‎（完卷时间：100分钟，满分：150分）‎ ‎2018.1‎ 一、选择题：（本大题共6题，每题4分，满分24分）‎ ‎1．如果把一个锐角三角形三边的长都扩大为原来的两倍，那么锐角A的余切值 ‎（A）扩大为原来的两倍； （B）缩小为原来的；‎ ‎（C）不变； （D）不能确定．‎ ‎2．下列函数中，二次函数是 ‎（A）； （B）； （C）；（D）.‎ ‎3．已知在Rt△ABC中，∠C=90°，AB=7，BC=5，那么下列式子中正确的是 ‎（A）； （B）； （C）； （D）．‎ ‎4．已知非零向量，，，下列条件中，不能判定向量与向量平行的是 ‎（A），； （B）； （C），； （D）．‎ ‎5．如果二次函数的图像全部在x轴的下方，那么下列判断中正确的是 ‎（A），； （B），；‎ ‎（C），； （D），．‎ B A F E C D ‎6．如图，已知点D、F在△ABC的边AB上，点E在边AC上，且DE∥BC，要使得EF∥CD，还需添加一个条件，这个条件可以是 ‎（A）； （B）；‎ ‎（C）； （D）．‎ ‎（第6题图）‎ 二、填空题：（本大题共12题，每题4分，满分48分）‎ ‎7．已知，则的值是 ．‎ ‎8．已知线段MN的长是4cm，点P是线段MN的黄金分割点，则较长线段MP的长是 ‎ cm．‎ ‎9．已知△ABC∽△A1B1C1，△ABC的周长与△A1B1C1的周长的比值是，BE、B1E1分别是它 ‎ 们对应边上的中线，且BE=6，则B1E1= ．‎ A D E B C F l1‎ l2‎ l3‎ l4‎ ‎（第14题图）‎ l5‎ ‎10．计算：= ．‎ ‎11．计算：= ．‎ ‎12．抛物线的最低点坐标是 ．‎ ‎13．将抛物线向下平移3个单位，所得的抛物线的表达式是 ．‎ ‎14．如图，已知直线l1、l2、l3分别交直线l4于点A、B、C，交直线l5于点D、E、F，且l1∥l2∥l3，AB=4，AC=6，DF=9，则DE= ．‎ ‎15．如图，用长为10米的篱笆，一面靠墙（墙的长度超过10米），围成一个矩形花圃，设矩形垂直于墙的一边长为x米，花圃面积为S平方米，则S关于x的函数解析式是 ．‎ ‎（不写定义域）．‎ ‎16．如图，湖心岛上有一凉亭B，在凉亭B的正东湖边有一棵大树A，在湖边的C处测得B在北偏西45°方向上，测得A在北偏东30°方向上，又测得A、C之间的距离为100米，则A、B之间的距离是 米（结果保留根号形式）．‎ ‎17．已知点（-1，）、（2，）在二次函数的图像上，如果>，那么 ‎ 0（用“>”或“<”连接）．‎ ‎18．如图，已知在Rt△ABC中，∠ACB=90°，，BC=8，点D在边BC上，将 ‎△ABC沿着过点D的一条直线翻折，使点B落在AB边上的点E处，联结CE、DE，当∠BDE=∠AEC时，则BE的长是 ．‎ ‎ ‎ C B A ‎45°‎ ‎30°‎ C B A ‎（第15题图）‎ ‎（第18题图）‎ ‎（第16题图）‎ 三、解答题：（本大题共7题，满分78分）‎ ‎19．（本题满分10分）‎ 将抛物线向左平移4个单位，求平移后抛物线的表达式、顶点坐标 和对称轴．‎ ‎（第20题图）‎ A B C D E ‎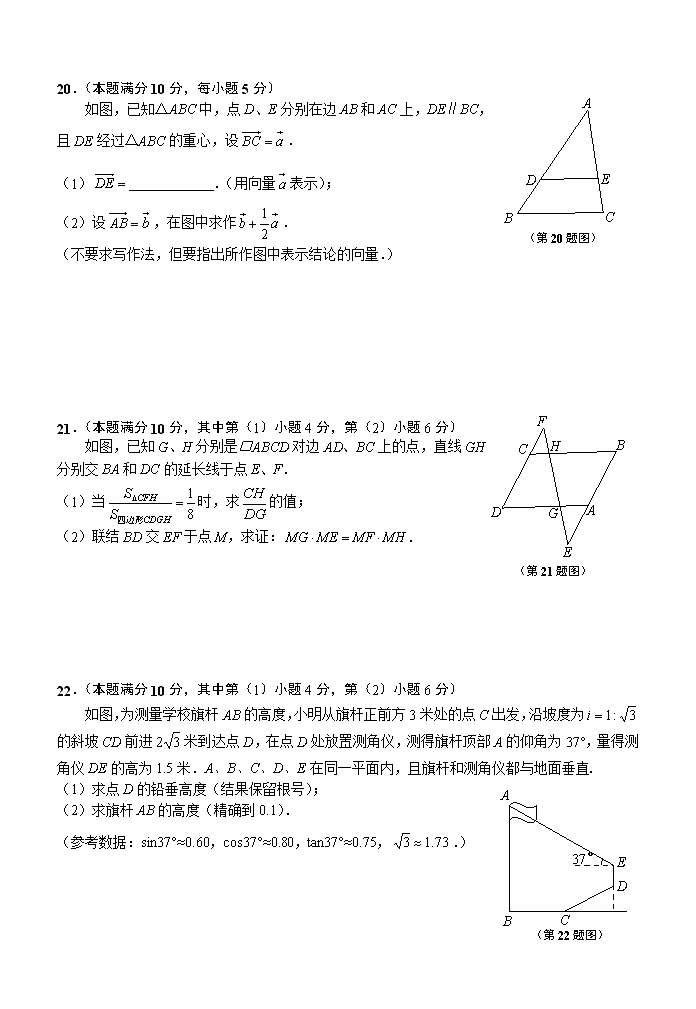20．（本题满分10分，每小题5分）‎ 如图，已知△ABC中，点D、E分别在边AB和AC上，DE∥BC，‎ 且DE经过△ABC的重心，设．‎ ‎（1） ．（用向量表示）；‎ ‎（2）设，在图中求作．‎ ‎（不要求写作法，但要指出所作图中表示结论的向量．）‎ ‎（第21题图）‎ A B H F E C G D ‎21．（本题满分10分，其中第（1）小题4分，第（2）小题6分） ‎ 如图，已知G、H分别是□ABCD对边AD、BC上的点，直线GH 分别交BA和DC的延长线于点E、F．‎ ‎（1）当时，求的值；‎ ‎（2）联结BD交EF于点M，求证：.‎ ‎22．（本题满分10分，其中第（1）小题4分，第（2）小题6分）‎ 如图，为测量学校旗杆AB的高度，小明从旗杆正前方3米处的点C出发，沿坡度为的斜坡CD前进米到达点D，在点D处放置测角仪，测得旗杆顶部A的仰角为37°，量得测角仪DE的高为1.5米．A、B、C、D、E在同一平面内，且旗杆和测角仪都与地面垂直. ‎ ‎（第22题图）‎ A B C D E ‎37°‎ ‎（1）求点D的铅垂高度（结果保留根号）；‎ ‎（2）求旗杆AB的高度（精确到0.1）．‎ ‎（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，．）‎ ‎23．（本题满分12分，其中第（1）小题6分，第（2）小题6分）‎ A ‎（第23题图）‎ D E F B C 如图，已知，在锐角△ABC中，CE⊥AB于点E，点D在边AC上，‎ 联结BD交CE于点F，且.‎ ‎（1）求证：BD⊥AC；‎ ‎（2）联结AF，求证：.‎ ‎24．（本题满分12分，每小题4分）‎ 已知抛物线y＝ax2＋bx＋5与x轴交于点A(1，0)和点B(5，0)，顶点为M．点C在x轴的负半轴上，且AC＝AB，点D的坐标为(0，3)，直线l经过点C、D．‎ ‎（1）求抛物线的表达式；‎ ‎（2）点P是直线l在第三象限上的点，联结AP，且线段CP是线段CA、CB的比例中项，‎ 求tan∠CPA的值；‎ y x ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎–1‎ ‎–2‎ ‎–3‎ ‎–4‎ ‎–5‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎–1‎ ‎–2‎ ‎–3‎ ‎–4‎ ‎–5‎ O ‎（3）在（2）的条件下，联结AM、BM，在直线PM上是否存在点 E，使得∠AEM=∠AMB.若存在，求出点E的坐标；若不存在，请说明理由．‎ ‎（第24题图）‎ ‎25．（本题满分14分，其中第（1）小题4分，第（2）小题5分，第（3）小题5分）‎ 如图，已知在△ABC中，∠ACB=90°，BC=2，AC=4，点D在射线BC上，以点D为圆心，BD为半径画弧交边AB于点E，过点E作EF⊥AB交边AC于点F，射线ED交射线AC于点G．‎ ‎（1）求证：△EFG∽△AEG；‎ ‎（2）设FG=x，△EFG的面积为y，求y关于x的函数解析式并写出定义域；‎ ‎（3）联结DF，当△EFD是等腰三角形时，请直接写出FG的长度．‎ A B C A B C C ‎（第25题图）‎ A B G F D E ‎ ‎ ‎（第25题备用图）‎ ‎（第25题备用图）‎ 浦东新区2017学年度第一学期初三教学质量检测 数学试卷参考答案及评分标准 一、选择题：（本大题共6题，每题4分，满分24分）‎ ‎1．C； 2．B； 3．A； 4．B； 5．D； 6．C． ‎ 二、填空题：（本大题共12题，每题4分，满分48分）‎ ‎7．；8．； 9．4；10．；11．；12．（0,-4）； ‎ ‎13．； 14．6； 15．；16．；17．>；18．．‎ 三、解答题：（本大题共7题，满分78分）‎ ‎19．解：∵=．…………………………………（3分）‎ ‎∴平移后的函数解析式是．………………………………（3分）‎ ‎ 顶点坐标是（-2，1）．……………………………………………………（2分）‎ ‎ 对称轴是直线．………………………………………………… （2分）‎ ‎（第20题图）‎ A B C D E F ‎20．解：（1）．……………………………（5分）‎ ‎（2）图正确得4分，‎ 结论：就是所要求作的向量． …（1分）．‎ ‎21．（1）解：∵，‎ ‎∴ ． ……………………………………………………（1分）‎ ‎∵ □ABCD中，AD//BC,‎ ‎ ∴ △CFH∽△DFG ． ………………………………………………（1分）‎ ‎ ∴ ．…………………………………………… （1分）‎ ‎（第21题图）‎ A B H F E C G D M ‎ ∴ ． …………………………………………………………（1分）‎ ‎（2）证明：∵ □ABCD中，AD//BC，‎ ‎ ∴ ． ……………………………………（2分）‎ ‎ ∵ □ABCD中，AB//CD，‎ ‎ ∴ ． ……………………………………（2分）‎ ‎ ∴ ． ……………………………………（1分）‎ ‎ ∴ ． ……………………………（1分）‎ ‎22．解：（1）延长ED交射线BC于点H.‎ 由题意得DH⊥BC.‎ 在Rt△CDH中，∠DHC=90°，tan∠DCH=.……………（1分）‎ ‎（第22题图）‎ A B C D E ‎37°‎ F H ‎∴ ∠DCH=30°．‎ ‎∴ CD=2DH．……………………………（1分）‎ ‎∵ CD=，‎ ‎∴ DH=，CH=3 .……………………（1分）‎ 答：点D的铅垂高度是米.…………（1分）‎ ‎（2）过点E作EF⊥AB于F.‎ 由题意得，∠AEF即为点E观察点A时的仰角，∴ ∠AEF=37°.‎ ‎∵ EF⊥AB，AB⊥BC，ED⊥BC，‎ ‎∴ ∠BFE=∠B=∠BHE=90°.‎ ‎∴ 四边形FBHE为矩形.‎ ‎∴ EF=BH=BC+CH=6. ……………………………………………（1分）‎ FB=EH=ED+DH=1.5+. ……………………………………（1分）‎ 在Rt△AEF中，∠AFE=90°，.（1分）‎ ‎∴ AB=AF+FB=6+ ………………………………………………（1分）‎ ‎ . ……………………………………………（1分）‎ 答：旗杆AB的高度约为7.7米. …………………………………（1分）‎ ‎23．证明：（1）∵ ，‎ A ‎（第23题图）‎ D E F B C ‎∴ . ………………………（1分）‎ ‎∵ ∠EFB=∠DFC， …………………（1分）‎ ‎∴ △EFB∽△DFC. …………………（1分）‎ ‎∴ ∠FEB=∠FDC. ………………… （1分）‎ ‎∵ CE⊥AB，‎ ‎∴ ∠FEB= 90°.……………………… （1分）‎ ‎∴ ∠FDC= 90°.‎ ‎∴ BD⊥AC. ………………………… （1分）‎ ‎（2）∵ △EFB∽△DFC，‎ ‎ ∴ ∠ABD =∠ACE. …………………………………………… （1分） ‎ ‎ ∵ CE⊥AB，‎ ‎∴ ∠FEB= ∠AEC= 90°.‎ ‎ ∴ △AEC∽△FEB. ……………………………………………（1分）‎ ‎ ∴ .……………………………………………………（1分）‎ ‎ ∴ . …………………………………………………（1分）‎ ‎∵ ∠AEC=∠FEB= 90°，‎ ‎ ∴ △AEF∽△CEB.………………………………………………（1分） ‎ ‎ ∴ ，∴ . ………………………（1分）‎ ‎24．解：（1）∵ 抛物线与轴交于点A（1，0），B（5，0），‎ M P ‎ D H ‎ N ‎ E ‎ C A B O x y l ‎ ∴ ……………………… …（1分） ‎ ‎ 解得 …………………………（2分） ‎ ‎ ∴ 抛物线的解析式为 .……（1分） ‎ ‎ （2）∵ A（1，0），B（5，0），‎ ‎（第24题图）‎ ‎ ∴ OA=1，AB=4.‎ ‎ ∵ AC=AB且点C在点A的左侧，∴ AC=4 .‎ ‎∴ CB=CA+AB=8. ………………………………………………（1分）‎ ‎ ∵ 线段CP是线段CA、CB的比例中项，∴ .‎ ‎∴ CP=. ……………………………………………………（1分）‎ ‎ 又 ∵ ∠PCB是公共角，‎ ‎∴ △CPA∽△CBP . ‎ ‎∴ ∠CPA= ∠CBP. ………………………………………………（1分）‎ ‎ 过P作PH⊥x轴于H.‎ ‎ ∵ OC=OD=3，∠DOC=90°，‎ ‎∴ ∠DCO=45°.∴ ∠PCH=45° ‎ ‎∴ PH=CH=CP=4，‎ ‎∴ H（-7，0），BH=12. ∴ P（-7，-4）.‎ ‎∴ ，. ………………………（1分）‎ ‎ （3） ∵ 抛物线的顶点是M（3，-4），………………………………… （1分） ‎ ‎ 又 ∵ P（-7，-4），∴ PM∥x轴 . ‎ ‎ 当点E在M左侧， 则∠BAM=∠AME.‎ ‎ ∵ ∠AEM=∠AMB， ‎ ‎∴ △AEM∽△BMA.…………………………………………………（1分）‎ ‎ ∴. ∴ .‎ ‎ ∴ ME=5，∴ E（-2，-4）. …………………………………（1分） ‎ ‎ 过点A作AN⊥PM于点N，则N（1，-4）.‎ ‎ 当点E在M右侧时，记为点，‎ ‎ ∵ ∠AN=∠AEN，‎ ‎∴ 点与E 关于直线AN对称，则（4，-4）.………………（1分） ‎ 综上所述，E的坐标为（-2，-4）或（4，-4）.‎ C ‎（第25题图）‎ A B G F D E H ‎25．解：（1）∵ ED=BD，‎ ‎∴ ∠B=∠BED．………………………………（1分）‎ ‎∵ ∠ACB=90°，‎ ‎∴ ∠B+∠A=90°．‎ ‎∵ EF⊥AB，‎ ‎∴ ∠BEF=90°．‎ ‎∴ ∠BED+∠GEF=90°．‎ ‎∴ ∠A=∠GEF． ………………………………（1分）‎ ‎∵ ∠G是公共角， ……………………………（1分）‎ ‎∴ △EFG∽△AEG． …………………………（1分）‎ ‎（2）作EH⊥AF于点H．‎ ‎∵ 在Rt△ABC中，∠ACB=90°，BC=2，AC=4，‎ ‎∴ ．‎ ‎∴ 在Rt△AEF中，∠AEF=90°，．‎ ‎∵ △EFG∽△AEG，‎ ‎∴ ．……………………………………………（1分）‎ ‎∵ FG=x，‎ ‎∴ EG=2x，AG=4x．‎ ‎∴ AF=3x． ……………………………………………………………（1分）‎ ‎∵ EH⊥AF，‎ ‎∴ ∠AHE=∠EHF=90°．‎ ‎∴ ∠EFA+∠FEH=90°．‎ ‎∵ ∠AEF=90°，‎ ‎∴ ∠A+∠EFA=90°．‎ ‎∴ ∠A=∠FEH．‎ ‎∴ tanA =tan∠FEH．‎ ‎∴ 在Rt△EHF中，∠EHF=90°，．‎ ‎∴ EH=2HF．‎ ‎∵ 在Rt△AEH中，∠AHE=90°，．‎ ‎∴ AH=2EH．‎ ‎∴ AH=4HF．‎ ‎∴ AF=5HF．‎ ‎∴ HF=．‎ ‎∴ ．…………………………………………………………（1分）‎ ‎∴ ．………………………………（1分）‎ 定义域：（）． ……………………………………………（1分）‎ ‎（3）当△EFD为等腰三角形时，FG的长度是：．……（5分）‎