北京市房山2015中考一模数学试卷含答案 18页

‎2015年房山区初三毕业会考试卷 数学 一、选择题（本题共30分，每小题3分）下列各题均有四个选项，其中只有一个是符合题意的．用铅笔把“机读答题卡”上对应题目答案的相应字母处涂黑．‎ ‎1．如图，数轴上有A，B，C，D四个点，其中表示2的相反数的点是 A．点A B．点B C．点C D．点D ‎2.据海关统计，2015年前两个月，我国进出口总值为37900亿元人民币，将37900用科学记数法表示为 A．3.79×102 B．0.379×105 C．3.79×104 D．379×102 ‎ ‎3.一个不透明的布袋里装有7个只有颜色不同的球，其中3个红球，4个白球，从布袋中随机摸出一个球，则摸出红球的概率是 ‎ A. B. C. D.‎ ‎4.如图，直线 a∥b,点C在直线 上，∠DCB=90°，若∠1=70°， 则∠2的度数为 第4题图 A．20° B． 25° C．30° D． 40°‎ ‎5. 右图是某几何体的三视图,该几何体是 A. 圆柱 B.正方体 C. 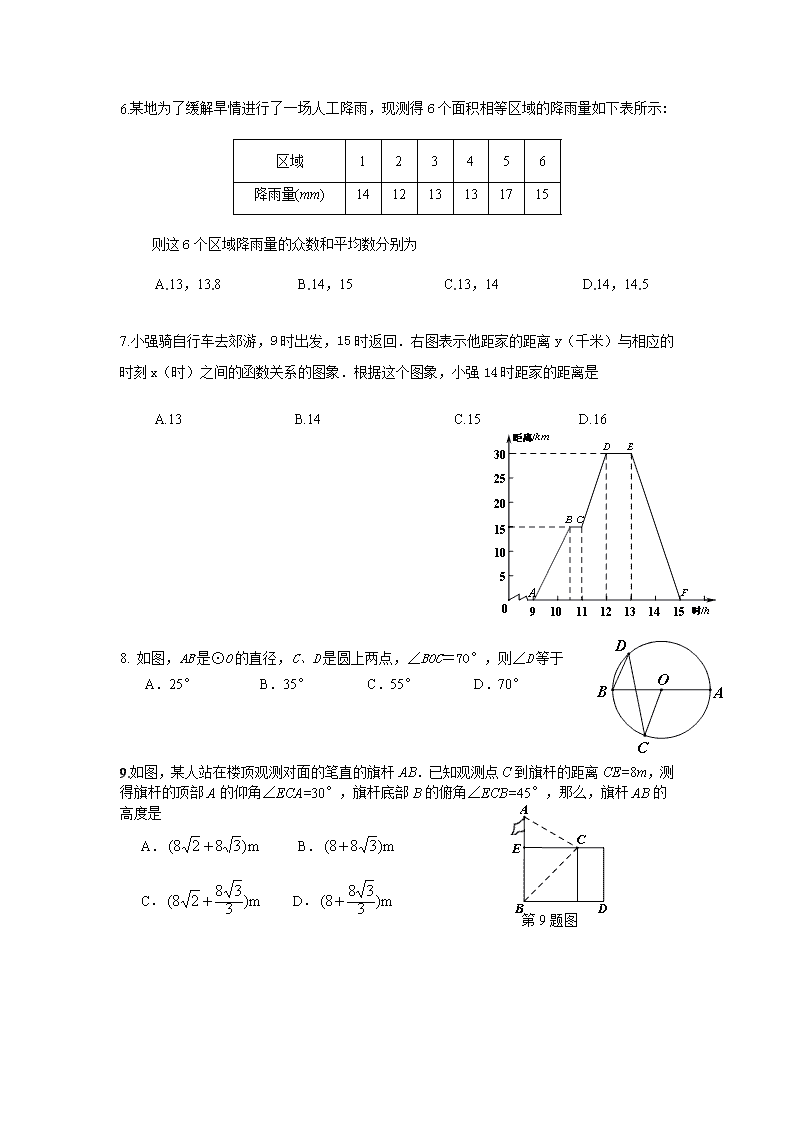圆锥 D.长方体 ‎6.某地为了缓解旱情进行了一场人工降雨，现测得6个面积相等区域的降雨量如下表所示:‎ 区域 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ 降雨量(mm)‎ ‎14‎ ‎12‎ ‎13‎ ‎13‎ ‎17‎ ‎15‎ ‎  则这6个区域降雨量的众数和平均数分别为 A.13，13.8 B.14，15 C.13，14 D.14，14.5‎ ‎7.小强骑自行车去郊游，9时出发，15时返回．右图表示他距家的距离y（千米）与相应的时刻x（时）之间的函数关系的图象．根据这个图象，小强14时距家的距离是 A.13 B.14 C.15 D.16‎ ‎8. 如图，AB是⊙O的直径，C、D是圆上两点，∠BOC＝70°，则∠D等于 A．25° B．35° C．55° D．70°‎ ‎9.如图，某人站在楼顶观测对面的笔直的旗杆AB．已知观测点C到旗杆的距离CE=8m，测得旗杆的顶部A的仰角∠ECA=30°，旗杆底部B的俯角∠ECB=45°，那么，旗杆AB的高度是 ‎ A． B．‎ 第9题图 ‎ C． D．‎ ‎10.如图，已知抛物线，把此抛物线沿y轴向上平移，平移后的抛物线和原抛物线与经过点,且平行于轴的两条直线所围成的阴影部分的面积为s，平移的距离为m,则下列图象中，能表示s与m的函数关系的图象大致是 A B C D 第10题图 二、填空题（本题共18分，每小题3分）‎ ‎11. 分解因式：＝________________.‎ ‎12.把代数式x2-4x+1化成 (x-h)2+k的形式，其结果是_____________．‎ ‎13.请写出一个随的增大而增大的反比例函数的表达式: ________________.‎ ‎14.甲、乙两人进行射击比赛，在相同条件下各射击10次．已知他们的平均成绩相同，方差分别是，，那么甲、乙两人成绩较为稳定的是________________.‎ ‎15.随着北京公交票制票价调整，公交集团更换了新版公交站牌，乘客在乘车时可以通过新版公交站牌计算乘车费用.新版站牌每一个站名上方都有一个对应的数字，将上下车站站名所对应数字相减取绝对值就是乘车路程，再按照其所在计价区段，参照票制规则计算票价.具体来说：‎ 乘车路程计价区段 ‎0-10‎ ‎11-15‎ ‎16-20‎ ‎...‎ 对应票价(元)‎ ‎2‎ ‎3‎ ‎4‎ ‎...‎ 另外，一卡通普通卡刷卡实行5折优惠，学生卡刷卡实行2.5折优惠.‎ 小明用学生卡乘车，上车时站名上对应的数字是5，下车时站名上对应的数字是22，那么，小明乘车的费用是________________元.‎ 第16题图 ‎16.如图,在平面直角坐标系中放置了5个正方形，点（0，2）在y轴上，点，，，，，，在x轴上，的坐标是（1，0）,∥∥．则点A1到x轴的距离是________________，点A2到x轴的距离是________________，点A3到x轴的距离是________________．‎ 三、解答题（本题共30分，每小题5分）‎ ‎17．计算：．‎ ‎18.解不等式，并把它的解集在数轴上表示出来．‎ 第19题图 ‎19.如图，CE=CB，CD=CA，∠DCA=∠ECB．求证：DE=AB．‎ ‎20.已知，求代数式的值.‎ ‎21.如图，在平面直角坐标系xOy中，一次函数y=kx+b（k≠0）的图象经过A（0，﹣2），‎ 第21题图 B（1，0）两点，与反比例函数（m≠0）的图象在第一象限内交于点M，若△OBM的面积是2．‎ ‎（1）求一次函数和反比例函数的表达式；‎ ‎（2）若点P是x轴上一点，且满足△AMP是以AM为直角边的直角三角形,请直接写出点P的坐标．‎ ‎ ‎ ‎22.列方程或方程组解应用题 为了鼓励市民节约用电，某市对居民用电实行“阶梯收费”（总电费=第一阶梯电费+第二阶梯电费）.规定：用电量不超过200度按第一阶梯电价收费，超过200度的部分按第二阶梯电价收费．下图是张磊家2014年3月和4月所交电费的收据：‎ 请问该市规定的第一阶梯电价和第二阶梯电价分别为每度多少元？‎ 四、解答题（本题共20分，每小题5分）‎ ‎23．如图，在菱形ABCD中，对角线AC、BD相交于点O，过点O作一条直线分别交DA、BC的延长线于点E、F，连接BE、DF．‎ ‎（1）求证：四边形BFDE是平行四边形；‎ ‎（2）若AB=4，CF=1，∠ABC=60°，求的值．‎ ‎24. 某校开展“人人读书”活动.小明为调查同学们的阅读兴趣，抽样调查了40名学生在本校图书馆的借阅情况（每人每次只能借阅一本图书），绘制了统计图1. 并根据图书馆各类图书所占比例情况绘制了统计图2,已知综合类图书有40本.‎ 图2‎ 图1‎ 校图书馆各类图书所占比例统计图 各类图书借阅人次分布统计图 ‎（1）补全统计图1；‎ ‎（2）该校图书馆共有图书________________本；‎ ‎（3）若该校共有学生1000人，试估算，借阅文学类图书的有______________人.‎ ‎25．如图，AB为⊙O直径，C是⊙O上一点，CO⊥AB于点O，弦CD与AB交于点F，过点D作∠CDE，使∠CDE=∠DFE，交AB的延长线于点E. 过点A作⊙O的切线交ED的延长线于点G.‎ ‎（1）求证：GE是⊙O的切线；‎ ‎（2）若OF：OB=1：3，⊙O的半径为3，求AG的长．‎ 第25题图 ‎26.小明遇到这样一个问题：‎ 如图1，在锐角△ABC中，AD、BE、CF分别为△ABC的高，求证：∠AFE=∠ACB.‎ 小明是这样思考问题的：如图2，以BC为直径做半⊙O，则点F、E在⊙O上，‎ ‎∠BFE+∠BCE=180°，所以∠AFE=∠ACB.‎ 请回答：若∠ABC=，则∠AEF的度数是 .‎ 参考小明思考问题的方法，解决问题：‎ 图1 图2 图3‎ 如图3，在锐角△ABC中，AD、BE、CF分别为△ABC的高，求证：∠BDF=∠CDE.‎ 五、解答题（本题共22分，第27题7分，第28题7分，第29题8分）‎ ‎27. 在平面直角坐标系中，抛物线与轴的两个交点分别为A（-3，0）,‎ B（1，0），顶点为C.‎ ‎(1) 求抛物线的表达式和顶点坐标；‎ ‎(2) 过点C作CH⊥x轴于点H，若点P为x轴上方的抛物线上一动点（点P与顶点C不重合），PQ⊥AC于点Q，当△PCQ与△ACH相似时，求点P的坐标.‎ ‎28．如图1，已知线段BC=2，点B关于直线AC的对称点是点D，点E为射线CA上一点，且ED=BD，连接DE，BE.‎ (1) 依题意补全图1，并证明：△BDE为等边三角形；‎ (2) 若∠ACB=45°，点C关于直线BD的对称点为点F，连接FD、FB.将△CDE绕点D 顺时针旋转α度（0°＜α＜360°）得到△，点E的对应点为E′，点C的对应点为点C′.‎ ‎①如图2，当α=30°时，连接．证明：=；‎ ‎　　②如图3，点M为DC中点，点P为线段上的任意一点，试探究：在此旋转过程中，线段PM长度的取值范围？‎ 图1‎ 图2‎ 图3‎ ‎29.【探究】如图1，点是抛物线上的任意一点，l是过点且与轴平行的直线，过点N作直线NH⊥l，垂足为H. ‎ ‎①计算: m=0时，NH= ; m=4时，NO= .‎ ‎②猜想: m取任意值时，NO NH(填“＞”、“＝”或“＜”).‎ ‎【定义】我们定义：平面内到一个定点F和一条直线l（点F不在直线l上）距离相等的点的集合叫做抛物线，其中点F叫做抛物线的“焦点”，直线l叫做抛物线的“准线”.如图1中的点O即为抛物线的“焦点”，直线l:即为抛物线的“准线”.可以发现“焦点”F在抛物线的对称轴上.‎ ‎【应用】（1）如图2，“焦点”为F(-4，-1)、“准线”为l的抛物线与y轴交于点N（0，2），点M为直线FN与抛物线的另一交点.MQ⊥l于点Q，直线l交y轴于点H.‎ ‎①直接写出抛物线y2的“准线”l： ；‎ ‎②计算求值： 图2‎ 图3‎ 图1‎ ‎（2）如图3，在平面直角坐标系xOy中，以原点O为圆心，半径为1的⊙O与x轴分别交于A、B两点（A在B的左侧），直线与⊙O只有一个公共点F，求以F为“焦点”、x轴为“准线”的抛物线的表达式.‎ ‎2015年房山区初中毕业会考试卷 数学参考答案和评分参考 一、选择题（本题共30分，每小题3分，）下列各题均有四个选项，其中只有一个是符合题意的．用铅笔把“机读答题卡”上对应题目答案的相应字母处涂黑．‎ ‎1．A 2．C 3．B 4．A 5． D 6．C 7．C 8．B 9．D 10．B 二、填空题（本题共18分，每小题3分）‎ ‎11． 12． 13．（答案不唯一） ‎ ‎14．甲 15．1 16．3,，‎ 三、解答题（本题共30分，每小题5分）‎ ‎17．原式= ………………………………………4分 ‎ =4 ………………………………………5分 ‎18．‎ ‎ ………………………………………1分 ‎ ………………………………………2分 ‎ ………………………………………3分 ‎ ………………………………………4分 ‎ …………5分 ‎19.∵，‎ ‎ ∴‎ ‎ ……………………1分 ‎∵‎ ‎ ………………………………………4分 ‎ ………………………………………5分 ‎20.原式=………………………………………1分 ‎ = ………………………………………2分 ‎ =‎ ‎ =‎ ‎ = ………………………………………3分 ‎ =‎ ‎ ………………………………………4分 原式= ………………………………………5分 ‎21.(1)一次函数解析式： ………………………………………2分 ‎ 反比例函数解析式： ………………………………………3分 ‎（2）或 ………………………………………5分 ‎22.设第一阶梯电价每度x元，第二阶梯电价每度y元，由题意可得：‎ ‎………………………………………1分 ‎ ………………………………………3分 解得 ………………………………………5分 答：第一阶梯电价每度0.5元，第二阶梯电价每度0.6元.‎ 四、解答题（本题共20分，每小题5分）‎ ‎23．（1）证明：在菱形ABCD中，AD∥BC，OA=OC，OB=OD，‎ ‎∴∠AEO=∠CFO，‎ ‎∴△AEO≌△CFO（AAS）‎ ‎∴OE=OF， ………………………………………1分 又∵OB=OD，‎ ‎∴四边形BFDE是平行四边形； ………………………………………2分 ‎（2）菱形ABCD,‎ ‎∴‎ 为等边三角形 ‎∴, ………………………………………3分 ‎∴‎ 作于M ‎∴‎ ‎ ………………………………………4分 ‎∴‎ ‎∴‎ ‎∴‎ 在中， ………………………………………5分 ‎24．‎ ‎（1）如图所示………………………………………1分 ‎(2) 800 ………………………………………3分 ‎（3）300 …………………………………5分 ‎25．（1）‎ 证明：连接OD ‎∵OC=OD，‎ ‎∴∠C=∠ODC ‎∵OC⊥AB ‎∴∠COF=90° ……………………………………1分 ‎∴∠OCD+∠CFO=90°‎ ‎∴∠ODC+∠CFO=90°‎ ‎∵∠EFD=∠FDE ‎∠EFD=∠CDE ‎∴∠CDO+∠CDE=90°‎ ‎∴DE为⊙O的切线………………………………2分 ‎（2）解：∵OF：OB=1：3，⊙O的半径为3，‎ ‎∴OF=1，‎ ‎∵∠EFD=∠EDF，‎ ‎∴EF=ED，‎ 在Rt△ODE中，OD=3，DE=x，则EF=x，OE=1+x，‎ ‎∵OD2+DE2=OE2，‎ ‎∴32+x2=（x+1）2，解得x=4……………………3分 ‎∴DE=4，OE=5，‎ ‎∵AG为⊙O的切线，‎ ‎∴AG⊥AE，‎ ‎∴∠GAE=90°， ‎ 而∠OED=∠GEA，‎ ‎∴Rt△EOD∽Rt△EGA， ………………………4分 ‎∴，即，‎ ‎∴AG=6．…………………………………………5分 ‎26. （1） ……………………1分 ‎（2）如图 由题意：∵,‎ ‎∴点A、E、D、B在以AB为直径的半圆上 ‎∴∠BAE+∠BDE=180°………………3分 又∵∠CDE+∠BDE=180°‎ ‎∴∠CDE=∠BAE ……………………4分 同理：点A、F、D、C在以AC为直径的半圆上.‎ ‎∴∠BDF=∠BAC ‎∴∠BDF =∠CDE ……………………5分 五、解答题（本题22分，第27题7分，第28题7分，第29题8分）‎ ‎27. （1）由题意，得 解得，‎ 抛物线的解析式为y=-x2-2x+3 ………………………2分 顶点C的坐标为（-1，4） ………………………3分 ‎（2）①若点P在对称轴右侧（如图①），只能是△PCQ∽△CAH，得∠QCP=∠CAH.‎ 延长CP交x轴于M，∴AM=CM，∴AM2=CM2.‎ 设M（m，0），则( m+3)2=42+(m+1)2，∴m=2，即M（2，0）.‎ 设直线CM的解析式为y=k1x+b1，‎ 则， 解之得，.‎ ‎∴直线CM的解析式.…………………………………4分 ‎，‎ 解得， (舍去).‎ ‎. ‎ ‎∴. ………………………………………………5分 ‎②若点P在对称轴左侧（如图②），只能是△PCQ∽△ACH，得∠PCQ=∠ACH.‎ 过A作CA的垂线交PC于点F，作FN⊥x轴于点N.‎ ‎ 由△CFA∽△CAH得，‎ 由△FNA∽△AHC得.‎ ‎ ∴, 点F坐标为（-5,1）. ‎ 设直线CF的解析式为y=k2x+b2，则，解之得.‎ ‎∴直线CF的解析式.……………………………………6分 ‎，‎ 解得， (舍去).‎ ‎∴. …………………………………7分 P A B H C Q M ‎（图①）‎ P A B H C Q F N ‎（图②）‎ ‎∴满足条件的点P坐标为或 ‎28.‎ 图1‎ 解：（1）补全图形，如图1所示； ……1分 证明：由题意可知：射线CA垂直平分BD ‎ ∴EB=ED ‎ ‎ 又∵ED=BD ‎ ∴EB=ED=BD ‎ ‎ ‎∴△EBD是等边三角形 ………………2分 ‎ ‎ 图2‎ ‎（2）①证明：如图2：由题意可知∠BCD=90°，BC=DC ‎ 又∵点C与点F关于BD对称 ‎ ∴四边形BCDF为正方形，‎ ‎∴∠FDC=90°,‎ ‎ ∵‎ ‎ ∴‎ ‎ 由（1）△BDE为等边三角形 ‎ ∴,ED=BD ‎ ∴ …………………3分 ‎ 又∵旋转得到的 图3（1）‎ ‎ ∴ ‎ ‎ ∴ ‎ ‎ ∴ …………………………4分 ‎②线段PM的取值范围是：‎ 设射线CA交BD于点O，‎ 图3（2）‎ I：如图3（1）‎ 当 ，D、M、P、C共线时，PM有最小值.‎ 此时DP=DO=，DM=1‎ ‎∴PM=DP-DM= ………………………5分 ‎ II：如图3（2）‎ ‎ 当点P与点重合，且P、D、M、C共线时，PM有最大值.‎ ‎ 此时DP=DE′=DE=DB=，DM=1‎ ‎ ∴PM= DP+DM=………………………6分 ‎∴线段PM的取值范围是：‎ ‎………………7分 ‎ ‎29.‎ 解：【探究】① 1 ; 5 ; ……………2分 ‎② ＝ . …………………3分 ‎ ‎ 图3‎ ‎ 【应用】（1）①； ……………………4分 ‎ ② 1 . ……………………5分 ‎ （2）如图3，设直线与x轴相交于点C. ‎ ‎ 由题意可知直线CF切⊙O于F，连接OF.‎ ‎∴∠OFC=90° ‎ ‎∴∠COF=60°‎ 又∵OF=1，‎ ‎∴OC=2 ‎ ‎ ∴ ‎ ‎ ∴“焦点”、.………6分 ‎ ∴抛物线的顶点为. ‎ ‎①当“焦点”为，顶点为， 时，‎ 易得直线CF1：. ‎ 过点A作AM⊥x轴，交直线CF1于点M.‎ ‎ ∴ ‎ ‎ ∴在抛物线上.‎ ‎ 设抛物线，将M点坐标代入可求得：‎ ‎ ∴………………………7分 ‎②当“焦点”为，顶点为，时，‎ 由中心对称性可得：‎ ‎ …………………………8分 综上所述：抛物线或.‎