2012福建厦门中考数学试卷 17页

‎2012年厦门市初中毕业及高中阶段各类学校招生考试 数 学 ‎（试卷满分：150分 考试时间：120分钟）‎ ‎ 准考证号 姓名 座位号 ‎ 注意事项：‎ ‎1．全卷三大题，26小题，试卷共4页，另有答题卡．‎ ‎2．答案一律写在答题卡上，否则不能得分．‎ ‎3．可直接用2B铅笔画图．‎ 一、选择题（本大题有7小题，每小题3分，共21分.每小题都有四个选项，其中有且只有一个选项正确）‎ ‎1． －2的相反数是 A．2 B．－‎2 ‎ C．±2 D．－ ‎2．下列事件中，是必然事件的是 A. 抛掷1枚硬币，掷得的结果是正面朝上 B. 抛掷1枚硬币，掷得的结果是反面朝上 C. 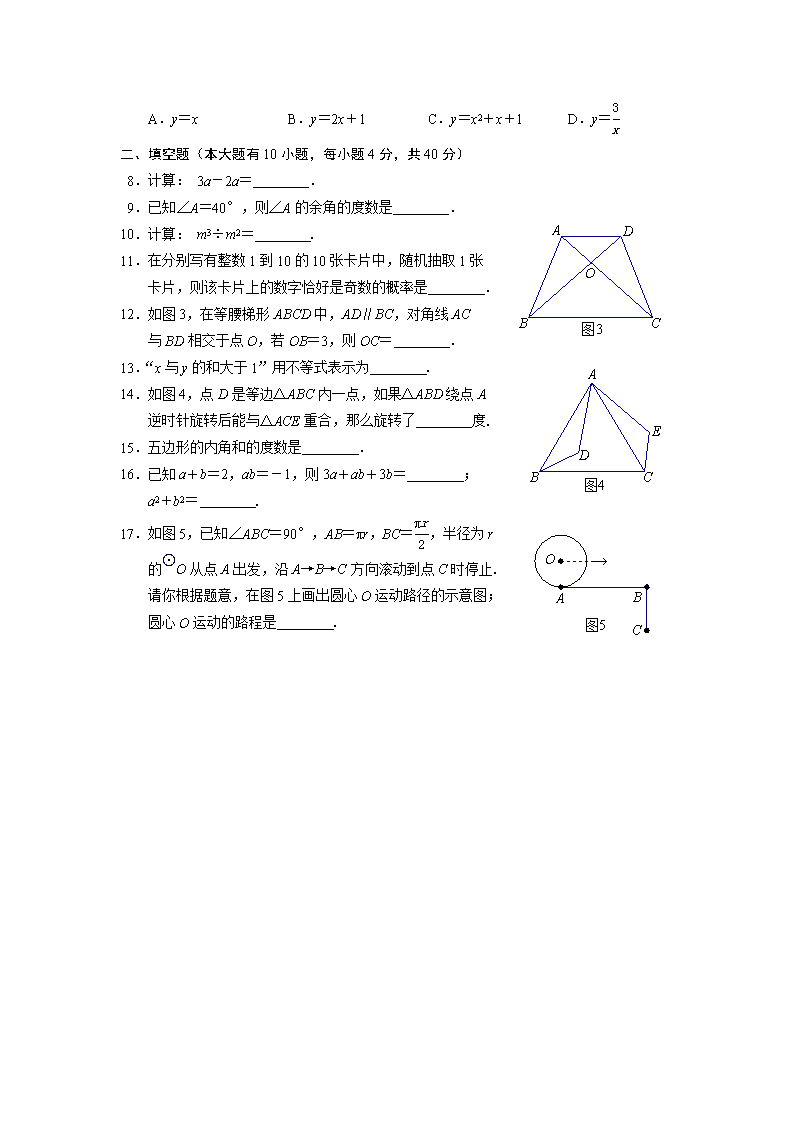抛掷1枚硬币，掷得的结果不是正面朝上就是反面朝上 D．抛掷2枚硬币，掷得的结果是1个正面朝上与1个反面朝上 ‎3．图1是一个立体图形的三视图，则这个立体图形是 A．圆锥 B．球 C．圆柱 D．三棱锥 ‎4．某种彩票的中奖机会是1%，下列说法正确的是 A．买1张这种彩票一定不会中奖 B．买1张这种彩票一定会中奖 C．买100张这种彩票一定会中奖 D．当购买彩票的数量很大时，中奖的频率稳定在1%‎ ‎5．若二次根式有意义，则x的取值范围是 A．x＞1 B．x≥1‎ C．x＜1 D．x≤1‎ ‎6．如图2，在菱形ABCD中，AC、BD是对角线，‎ 若∠BAC＝50°，则∠ABC等于 A．40° B．50°‎ C．80° D．100°‎ ‎7．已知两个变量x和y，它们之间的3组对应值如下表所示.‎ x ‎－1‎ ‎0‎ ‎1‎ y ‎－1‎ ‎1‎ ‎3‎ 则y 与x之间的函数关系式可能是 A．y＝x B．y＝2x＋‎1 ‎ C．y＝x2＋x＋1 D．y＝ 二、填空题（本大题有10小题，每小题4分，共40分）‎ ‎8．计算： ‎3a－‎2a＝ ．‎ ‎9．已知∠A＝40°，则∠A的余角的度数是 ．‎ ‎10．计算： m3÷m2＝ . ‎ ‎11．在分别写有整数1到10的10张卡片中，随机抽取1张 卡片，则该卡片上的数字恰好是奇数的概率是 ．‎ ‎12．如图3，在等腰梯形ABCD中，AD∥BC，对角线AC ‎ 与BD相交于点O，若OB＝3，则OC＝ ．‎ ‎13．“x与y的和大于‎1”‎用不等式表示为 .‎ ‎14．如图4，点D是等边△ABC内一点，如果△ABD绕点A ‎ 逆时针旋转后能与△ACE重合，那么旋转了 度.‎ ‎15．五边形的内角和的度数是 ．‎ ‎16．已知a＋b＝2，ab＝－1，则‎3a＋ab＋3b＝ ；‎ a2＋b2＝ .‎ ‎17．如图5，已知∠ABC＝90°，AB＝πr，BC＝，半径为r 的⊙O从点A出发，沿A→B→C方向滚动到点C时停止.‎ 请你根据题意，在图5上画出圆心O运动路径的示意图；‎ 圆心O运动的路程是 .‎ 三、解答题（本大题有9小题，共89分）‎ ‎18．（本题满分18分）‎ ‎（1）计算：4÷(－2)＋(－1)2×40； ‎ ‎（2）画出函数y＝－x＋1的图象；‎ ‎（3）已知：如图6，点B、F、C、E在一条直线上，‎ ‎∠A＝∠D，AC＝DF，且AC∥DF.‎ 求证：△ABC≌△DEF.‎ ‎19．（本题满分7分）解方程组： ‎20．（本题满分7分）已知：如图7，在△ABC中，∠C＝90°，点D、E分别在边AB、AC 上，DE∥BC，DE＝3， BC＝9.‎ ‎（1）求 的值；‎ ‎（2）若BD＝10，求sin∠A的值. ‎ ‎21.（本题满分7分）已知A组数据如下：‎ ‎0，1，－2，－1，0，－1，3.‎ ‎ （1）求A组数据的平均数；‎ ‎（2）从A组数据中选取5个数据，记这5个数据为B组数据. 要求B组数据满足两个条件：①它的平均数与A组数据的平均数相等；②它的方差比A组数据的方差大.你选取的B组数据是 ，请说明理由.‎ ‎【注：A组数据的方差的计算式是 SA2＝[(x1－)2＋(x2－)2＋(x3－)2＋(x4－)2＋(x5－)2＋(x6－)2＋(x7－)2]】‎ ‎22．（本题满分9分）工厂加工某种零件，经测试，单独加工完成这种零件，甲车床需用 x小时，乙车床需用 (x2－1)小时，丙车床需用(2x－2)小时. ‎ ‎（1）单独加工完成这种零件，若甲车床所用的时间是丙车床的 ，求乙车床单独加工完成这种零件所需的时间；‎ ‎（2）加工这种零件，乙车床的工作效率与丙车床的工作效率能否相同？请说明理由.‎ ‎23．（本题满分9分）已知：如图8，⊙O是△ABC的外接圆，AB为⊙O的直径，弦CD交AB于E，∠BCD＝∠BAC . ‎ ‎（1）求证：AC＝AD；‎ ‎（2）过点C作直线CF，交AB的延长线于点F，‎ 若∠BCF＝30°,则结论“CF一定是⊙O的切线”‎ 是否正确？若正确，请证明；若不正确，请举反例.‎ ‎24．（本题满分10分）如图9，在平面直角坐标系中，已知点A(2，3)、B(6，3)，连结AB. 如果点P在直线y＝x－1上，且点P到直线AB的距离小于1，那么称点P是线段AB的“邻近点”．‎ ‎　 （1）判断点Ｃ( ， ) 是否是线段AB的“邻近点”，并说明理由；‎ ‎（2）若点Q (m，n)是线段AB的“邻近点”，求m的取值范围．‎ ‎25．（本题满分10分）已知□ABCD，对角线AC与BD相交于点O，点P在边AD上，过点P分别作PE⊥AC、PF⊥BD，垂足分别为E、F，PE＝PF．‎ ‎ （1）如图10，若PE＝，EO＝1，求∠EPF的度数；‎ ‎ （2）若点P是AD的中点，点F是DO的中点，‎ BF ＝BC＋3－4，求BC的长．‎ ‎26．（本题满分12分）已知点A(1，c)和点B (3，d )是直线y＝k1x＋b与双曲线y＝（k2＞0）的交点．‎ ‎　 （1）过点A作AM⊥x轴，垂足为M，连结BM．若AM＝BM，求点B的坐标；‎ ‎ （2）设点P在线段AB上，过点P作PE⊥x轴，垂足为E，并交双曲线y＝（k2＞0）于点N．当 取最大值时，若PN＝ ，求此时双曲线的解析式．‎ ‎2012年厦门市初中毕业及高中阶段各类学校招生考试 数学参考答案及评分标准 说明：‎ ‎1．解答只列出试题的一种或几种解法．如果考生的解法与所列解法不同，可参照解答中评分标准相应评分；‎ ‎2．评阅试卷，要坚持每题评阅到底，不能因考生解答中出现错误而中断对本题的评阅．如果考生的解答在某一步出现错误，影响后续部分而未改变本题的内容和难度，视影响的程度决定后继部分的给分，但原则上不超过后续部分应得分数的一半；‎ ‎3．解答题评分时，给分或扣分均以1分为基本单位．‎ 一、选择题（本大题共7小题，每小题3分，共21分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ 选项 A C A D B C B 二、填空题（本大题共10小题，每题4分，共40分）‎ ‎8. a. 9. 50°. 10. m. 11. . ‎ 12. 3. 13‎. x＋y＞1. 14. 60.‎ ‎15. 540°. 16. 5； 6. 17. ；2πr.‎ 三、解答题（本大题共9小题，共89分）‎ ‎18．（本题满分18分）‎ ‎（1）解：4÷(－2) ＋(－1)2×40‎ ‎＝－2＋1×1 4分 ‎＝－2＋1 5分 ‎＝－1. 6分 ‎（2）解：正确画出坐标系 8分 正确写出两点坐标 10分 画出直线 12分 ‎（3）证明：∵ AC∥DF， ……13分 ‎∴ ∠ACB＝∠DFE. ……15分 又∵ ∠A＝∠D， ……16分 AC＝DF， ……17分 ‎∴ △ABC≌△EDF. ……18分 ‎19．（本题满分7分）‎ 解1： ‎ ‎①＋②，得 1分 ‎5x＝5， 2分 x＝1. 4分 将x＝1代入 ①，得 ‎3＋y＝4， 5分 y＝1． 6分 ‎∴ 7分 解2：由①得 y＝4－3x． ③ 1分 将③代入②，得 ‎2x－(4－3x) ＝1． 2分 得x＝1. 4分 将x＝1代入③ ，得 ‎ y＝4－3×1 5分 ‎＝1． 6分 ‎∴ 7分 ‎20．（本题满分7分）‎ ‎（1）解：∵ DE∥BC ，∴ △ADE∽△ABC. ……1分 ‎∴ ＝ . ……2分 ‎∴ ＝. ……3分 ‎（2）解1：∵ ＝，BD＝10，‎ ‎∴ ＝ 4分 ‎∴ AD＝5 5分 经检验，符合题意. ∴ AB＝15.‎ 在Rt△ABC中， 6分 sin∠A＝＝. 7分 ‎ 解2： ∵ ＝，BD＝10，‎ ‎∴ ＝ 4分 ‎∴ AD＝5 5分 经检验，符合题意.‎ ‎∵ DE∥BC，∠C＝90°‎ ‎∴ ∠AED＝90°‎ 在Rt△AED中， 6分 sin∠A＝＝. 7分 ‎ 解3：过点D作DG⊥BC，垂足为G. ∴ DG∥AC.‎ ‎∴∠A＝∠BDG. 4分 又∵ DE∥BC，∴四边形ECGD是平行四边形.‎ ‎∴ DE＝CG. 5分 ‎∴ BG＝6.‎ 在Rt△DGB中， 6分 ‎∴ sin∠BDG＝＝. 7分[来源:学科网]‎ ‎∴ sin∠A＝.‎ ‎21．（本题满分7分）‎ ‎（1）解：A组数据的平均数是 1分 ‎＝0. 3分 ‎（2）解1：选取的B组数据：0，－2，0，－1，3. 4分 ‎∵ B组数据的平均数是0. 5分 ‎∴ B组数据的平均数与A组数据的平均数相同. ‎ ‎∴ SB2＝ ，SA2＝ . 6分 ‎∴ ＞. 7分 ‎∴ B组数据：0，－2，0，－1，3.‎ ‎ 解2：B组数据：1，－2，－1，－1，3. 4分 ‎∵ B组数据的平均数是0. 5分 ‎∴ B组数据的平均数与A组数据的平均数相同. ‎ ‎∵SA2＝, SB2＝ . 6分 ‎ ‎∴＞ 7分 ‎∴ B组数据：1，－2，－1，－1，3. ‎ ‎22．（本题满分9分）‎ ‎（1）解:由题意得, ‎ x＝(2x－2) 1分 ‎∴ x＝4. 2分 ‎∴ x2－1＝16－1＝15(小时). 3分 答：乙车床单独加工完成这种零件所需的时间是15小时. 4分 ‎（2）解1：不相同. 5分 若乙车床的工作效率与丙车床的工作效率相同，由题意得, 6分 ＝ . 7分 ‎∴ ＝. ‎ ‎∴ x＝1. 8分 经检验，x＝1不是原方程的解. ∴ 原方程无解. 9分[来源:学科网ZXXK]‎ 答：乙车床的工作效率与丙车床的工作效率不相同.‎ ‎ 解2：不相同. 5分 若乙车床的工作效率与丙车床的工作效率相同，由题意得, 6分 x2－1＝2x－2. 7分 解得，x＝1. 8分 此时乙车床的工作时间为0小时，不合题意. 9分 答：乙车床的工作效率与丙车床的工作效率不相同. ‎ ‎23．（本题满分9分）‎ ‎（1）证明1：∵∠BCD＝∠BAC，‎ ‎∴ ＝ . ……1分 ‎∵ AB为⊙O的直径，‎ ‎∴ AB⊥CD， ……2分 CE＝DE. ……3分 ‎∴ AC＝AD . ……4分 ‎ 证明2：∵∠BCD＝∠BAC，‎ ‎∴ ＝ . 1分 ‎∵ AB为⊙O的直径， ∴ ＝ . 2分 ‎∴ ＝ . 3分 ‎∴ AC＝AD . 4分 ‎ 证明3：∵ AB为⊙O的直径，∴ ∠BCA＝90°. 1分 ‎∴ ∠BCD+∠DCA＝90°, ∠BAC+∠CBA＝90°‎ ‎∵∠BCD＝∠BAC，∴∠DCA＝∠CBA 2分 ‎∴ ＝ . 3分 ‎∴ AC＝AD . 4分 ‎（2）解1：不正确. 5分 连结OC.‎ 当 ∠CAB＝20°时， 6分 ‎∵ OC＝OA，有 ∠OCA＝20°.‎ ‎∵ ∠ACB＝90°， ∴ ∠OCB＝70°. 7分 又∵∠BCF＝30°，‎ ‎∴∠FCO＝100°， 8分 ‎∴ CO与FC不垂直. 9分 ‎∴ 此时CF不是⊙O的切线. ‎ ‎ 解2：不正确. 5分 连结OC.‎ 当 ∠CAB＝20°时， 6分 ‎∵ OC＝OA，有 ∠OCA＝20°.‎ ‎∵ ∠ACB＝90°， ∴ ∠OCB＝70°. 7分 又∵∠BCF＝30°，‎ ‎∴∠FCO＝100°， 8分 在线段FC的延长线上取一点G，如图所示，使得∠COG＝20°.‎ 在△OCG中， ∵∠GCO＝80°， ∴∠CGO＝80°.‎ ‎∴ OG＝OC. 即OG是⊙O的半径.‎ ‎∴ 点G在⊙O上. 即直线CF与圆有两个交点. 9分 ‎∴ 此时CF不是⊙O的切线.‎ ‎ 解3：不正确. 5分 连结OC.‎ 当 ∠CBA＝70°时， 6分 ‎∴ ∠OCB＝70°. 7分 又∵∠BCF＝30°，‎ ‎∴∠FCO＝100°， 8分 ‎∴ CO与FC不垂直. 9分 ‎∴ 此时CF不是⊙O的切线.‎ ‎24．（本题满分10分）‎ ‎（1）解：点Ｃ(，) 是线段AB的“邻近点”. 1分 ‎∵－1＝， ∴点Ｃ(，)在直线y＝x－1上. 2分[来源:学_科_网Z_X_X_K]‎ ‎∵点A的纵坐标与点B的纵坐标相同，‎ ‎∴ AB∥x轴. 3分 ‎∴Ｃ(，) 到线段AB的距离是3－，‎ ‎∵3－＝＜1， 4分 ‎∴Ｃ(，)是线段AB的“邻近点”.‎ ‎（2）解1：∵点Q(m，n)是线段AB的“邻近点”，‎ ‎∴ 点Q(m，n)在直线y＝x－1上，‎ ‎∴ n＝m－1. 5分 ‎① 当m≥4时， 6分 有n＝m－1≥3.‎ 又AB∥x轴，‎ ‎∴ 此时点Q(m，n)到线段AB的距离是n－3. 7分 ‎∴0≤n－3＜1.‎ ‎∴ 4≤m＜5. 8分 ‎② 当m≤4时， 9分 有n＝m－1≤3.‎ 又AB∥x轴，‎ ‎∴ 此时点Q(m，n)到线段AB的距离是3－n.‎ ‎∴0≤3－n＜1.‎ ‎∴ 3＜m≤4. 10分 综上所述， 3＜m＜5.‎ ‎ 解2：∵点Q(m，n)是线段AB的“邻近点”，‎ ‎∴ 点Q(m，n)在直线y＝x－1上，‎ ‎∴ n＝m－1. 5分 又AB∥x轴，‎ ‎∴ Q(m，n)到直线AB的距离是n－3或3－n， 6分 ‎① 当0≤n－3＜1时， 7分 即 当0≤m－1－3＜1时，‎ 得 4≤m＜5. 8分 ‎② 当0≤3－n＜1时， 9分 有0≤3－(m－1)＜1时，‎ 得 3＜m≤4. 10分 综上所述，3＜m＜5.‎ ‎25．（本题满分10分）‎ ‎（1）解1：连结PO , ‎ ‎∵ PE＝PF，PO＝PO，‎ PE⊥AC、PF⊥BD，‎ ‎∴ Rt△PEO≌Rt△PFO.‎ ‎∴ ∠EPO＝∠FPO. ……1分 在Rt△PEO中， ……2分 tan∠EPO＝＝， ……3分 ‎∴ ∠EPO＝30°. ‎ ‎∴ ∠EPF＝60°. 4分 ‎ 解2：连结PO ,‎ 在Rt△PEO中， 1分 PO＝ ＝2.‎ ‎∴ sin∠EPO＝＝. 2分 ‎∴ ∠EPO＝30°. 3分 在Rt△PFO中，cos∠FPO＝＝，∴∠FPO＝30°.‎ ‎∴ ∠EPF＝60°. 4分 ‎ 解3：连结PO ,‎ ‎∵ PE＝PF，PE⊥AC、PF⊥BD，垂足分别为E、F，‎ ‎∴ OP是∠EOF的平分线.‎ ‎∴ ∠EOP＝∠FOP. 1分 在Rt△PEO中， 2分 tan∠EOP＝＝ 3分 ‎∴ ∠EOP＝60°，∴ ∠EOF＝120°.‎ 又∵∠PEO＝∠PFO＝90°，‎ ‎∴ ∠EPF＝60°. 4分 ‎（2）解1：∵点P是AD的中点，∴ AP＝DP.‎ 又∵ PE＝PF，∴ Rt△PEA≌Rt△PFD.‎ ‎∴ ∠OAD＝∠ODA.‎ ‎∴ OA＝OD. 5分 ‎∴ AC＝2OA＝2OD＝BD.‎ ‎∴□ABCD是矩形. 6分 ‎ ‎∵ 点P是AD的中点，点F是DO的中点，‎ ‎∴ AO∥PF. 7分 ‎∵ PF⊥BD，∴ AC⊥BD.‎ ‎∴□ABCD是菱形. 8分 ‎∴□ABCD是正方形. 9分 ‎∴ BD＝BC. ‎ ‎∵ BF＝BD，∴BC＋3－4＝BC.‎ 解得，BC＝4. 10分 ‎ 解2：∵ 点P是AD的中点，点F是DO的中点，‎ ‎∴ AO∥PF. 5分 ‎∵ PF⊥BD，∴ AC⊥BD.‎ ‎∴□ABCD是菱形. 6分 ‎∵ PE⊥AC，∴ PE∥OD. ‎ ‎∴ △AEP∽△AOD.‎ ‎∴ ＝＝.‎ ‎∴ DO＝2PE.‎ ‎∵ PF是△DAO的中位线，‎ ‎∴ AO＝2PF.‎ ‎∵ PF＝PE，‎ ‎∴ AO＝OD. 7分 ‎∴ AC＝2OA＝2OD＝BD.‎ ‎∴ □ABCD是矩形. 8分 ‎∴ □ABCD是正方形. 9分 ‎∴ BD＝BC.‎ ‎∵ BF＝BD，∴BC＋3－4＝BC.‎ 解得，BC＝4. 10分 ‎ 解3：∵点P是AD的中点，∴ AP＝DP.‎ 又∵ PE＝PF， ∴ Rt△PEA≌Rt△PFD. ‎ ‎∴ ∠OAD＝∠ODA.‎ ‎∴ OA＝OD. 5分 ‎∴ AC＝2OA＝2OD＝BD.‎ ‎∴□ABCD是矩形. 6分 ‎ ‎∵点P是AD的中点，点O是BD的中点，连结PO.‎ ‎∴PO是△ABD的中位线，‎ ‎∴ AB＝2PO. 7分 ‎∵ PF⊥OD，点F是OD的中点，‎ ‎∴ PO＝PD.‎ ‎∴ AD＝2PO.‎ ‎∴ AB＝AD. 8分 ‎∴□ABCD是正方形. 9分 ‎ ‎∴ BD＝BC.‎ ‎∵ BF＝BD，∴BC＋3－4＝BC.‎ 解得，BC＝4. 10分 ‎ 解4：∵点P是AD的中点，∴ AP＝DP.‎ 又∵ PE＝PF， ∴ Rt△PEA≌Rt△PFD.‎ ‎∴ ∠OAD＝∠ODA.‎ ‎∴ OA＝OD. 5分 ‎∴ AC＝2OA＝2OD＝BD.‎ ‎∴□ABCD是矩形. 6分 ‎ ‎∵PF⊥OD，点F是OD的中点，连结PO.‎ ‎∴PF是线段OD的中垂线，‎ 又∵点P是AD的中点，‎ ‎∴PO＝PD＝BD 7分 ‎∴△AOD 是直角三角形, ∠AOD＝90°. 8分 ‎∴□ABCD是正方形. 9分 ‎ ‎∴ BD＝BC.‎ ‎∵ BF＝BD，∴BC＋3－4＝BC.‎ 解得，BC＝4. 10分 ‎26．（本题满分12分）‎ ‎（1）解：∵点A(1，c)和点B (3，d )在双曲线y＝（k2＞0）上，‎ ‎∴ c＝k2＝3d 1分 ‎∵ k2＞0， ∴ c＞0，d＞0. ‎ A(1，c)和点B (3，d )都在第一象限.‎ ‎∴ AM＝3d. 2分 过点B作BT⊥AM，垂足为T.‎ ‎∴ BT＝2. 3分 TM＝d.‎ ‎∵ AM＝BM， ∴ BM＝3d. ‎ 在Rt△BTM中，TM 2＋BT2＝BM2，‎ ‎∴ d2＋4＝9d2， ∴ d＝. ‎ 点B(3，) . 4分 ‎（2）解1：∵ 点A(1，c)、B(3，d)是直线y＝k1x＋b与双曲线y＝（k2＞0）的交点，‎ ‎∴ c＝k2,，3d＝k2，c＝k1＋b，d＝3k1＋b. 5分 ‎∴ k1＝－k2，b＝k2. ‎ ‎∵ A(1，c)和点B (3，d )都在第一象限，∴ 点P在第一象限.‎ ‎∴ ＝ ‎ ‎＝x2＋x ‎＝－x2＋x. 6分 ‎∵ 当x＝1，3时，＝1；‎ 又∵当x＝2时， 的最大值是.‎ ‎∴ 1≤≤. 7分 ‎∴ PE≥NE. 8分 ‎∴ ＝－1＝－x2＋x－1. 9分 ‎∴ 当x＝2时，‎ 的最大值是. 10分 由题意，此时PN＝，‎ ‎∴ NE＝. 11分 ‎∴ 点N(2，) . ∴ k2＝3.‎ ‎∴ y＝. 12分 ‎ 解2：∵ A(1，c)和点B (3，d )都在第一象限，∴ 点P在第一象限.‎ ‎∵ ＝ ＝x2＋x，‎ 当点P与点A、B重合时，＝1，‎ 即当x＝1或3时，＝1. ‎ ‎∴ 有 ＋＝－1， ＋＝－1. 5分 解得，k1＝－k2，b＝k2.‎ ‎∴ ＝－x2＋x. 6分 ‎∵ k2＝－3k1，k2＞0，∴ k1＜0.‎ ‎∵ PE－NE＝k1x＋b－＝k1x－4k1＋ ‎＝k1( )＝ ， 7分 又∵当1≤x≤3时，‎ ‎(x－1) (x－3) ≤0，‎ ‎∴ k1( ) ≥0.‎ ‎∴ PE－NE≥0. 8分 ‎∴ ＝－1‎ ‎＝－x2＋x－1. 9分[来源:Zxxk.Com]‎ ‎∴ 当x＝2时，的最大值是. 10分 由题意，此时PN＝，‎ ‎∴ NE＝. 11分 ‎∴ 点N(2，) . ∴ k2＝3.‎ ‎∴ y＝. 12分 ‎ 解3：∵ 点A(1，c)、B(3，d)是直线y＝k1x＋b与双曲线y＝（k2＞0）的交点，‎ ‎∴ c＝k2,，3d＝k2，c＝k1＋b，d＝3k1＋b. 5分 k2＝3d， k1＝－d，b＝4d.‎ ‎∴ 直线y＝－dx＋4d，双曲线y＝. [来源:学科网ZXXK]‎ ‎∵ A(1，c)和点B (3，d )都在第一象限，∴ 点P在第一象限.‎ ‎∴ PN＝PE－NE＝－dx＋4d－ ‎＝－d( )＝－ ， 6分 又∵当1≤x≤3时，(x－1) (x－3) ≤0，‎ ‎∴－ ≥0.‎ ‎∴ PN＝PE－NE≥0. 7分 ‎∴ ＝ 8分 ‎＝－x2＋x－1. 9分 ‎∴ 当x＝2时，的最大值是. 10分 由题意，此时PN＝，‎ ‎∴ NE＝. 11分 ‎∴ 点N(2，) .‎ ‎∴ k2＝3.‎ ‎∴ y＝. 12分