中考数学几何证明题模拟题 7页

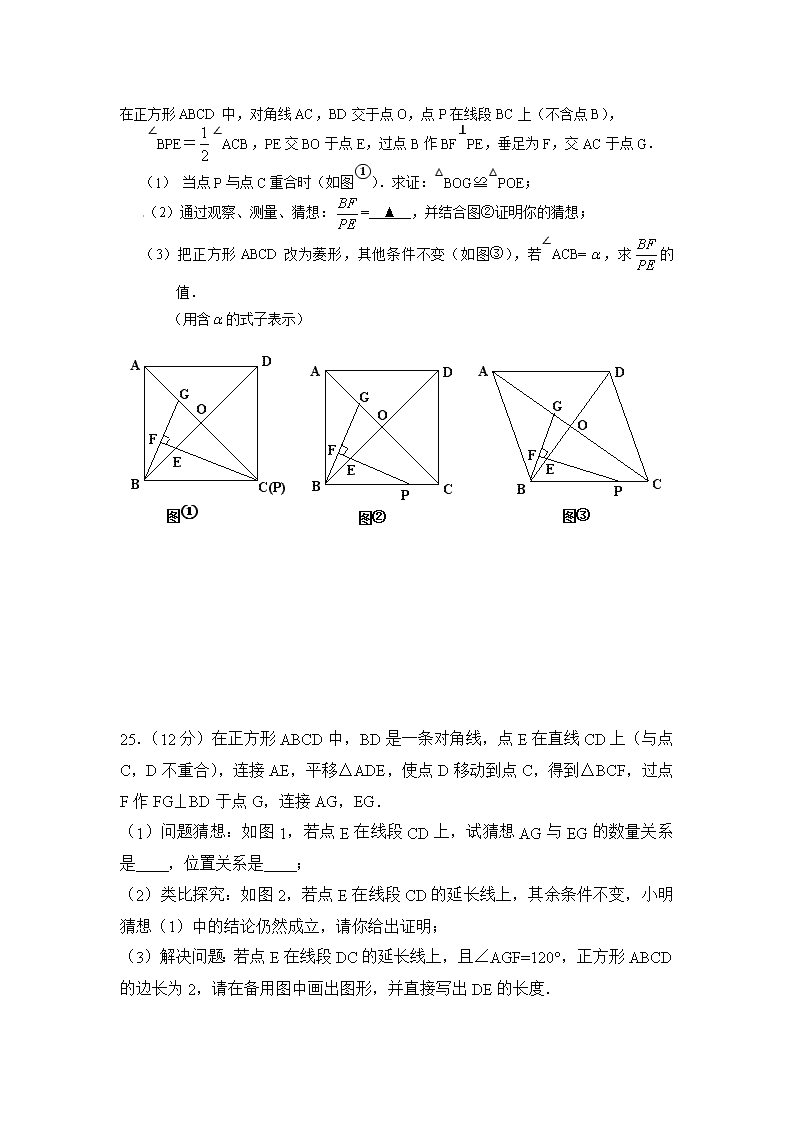
在正方形ABCD中，对角线AC，BD交于点O，点P在线段BC上（不含点B），‎ ‎∠BPE＝∠ACB，PE交BO于点E，过点B作BF⊥PE，垂足为F，交AC于点G．‎ ‎（1） 当点P与点C重合时（如图①）．求证：△BOG≌△POE；‎ ‎（2）通过观察、测量、猜想：= ▲ ，并结合图②证明你的猜想；‎ ‎（3）把正方形ABCD改为菱形，其他条件不变（如图③），若∠ACB=，求的值．‎ ‎（用含的式子表示）‎ A B C(P)‎ D E F O G 图①‎ A B C D P E O G F 图②‎ A B C D P E F ‎ O G 图③‎ ‎[来源:学科网ZXXK]‎ ‎25．（12分）在正方形ABCD中，BD是一条对角线，点E在直线CD上（与点C，D不重合），连接AE，平移△ADE，使点D移动到点C，得到△BCF，过点F作FG⊥BD于点G，连接AG，EG．‎ ‎（1）问题猜想：如图1，若点E在线段CD上，试猜想AG与EG的数量关系是　　，位置关系是　　；‎ ‎（2）类比探究：如图2，若点E在线段CD的延长线上，其余条件不变，小明猜想（1）中的结论仍然成立，请你给出证明；‎ ‎（3）解决问题：若点E在线段DC的延长线上，且∠AGF=120°，正方形ABCD的边长为2，请在备用图中画出图形，并直接写出DE的长度．‎ 已知，点D为直线BC上一动点（点D不与点B、C重合），∠BAC=90°，AB=AC，∠DAE=90°，AD=AE，连接CE．‎ ‎（l）如图1，当点D在线段BC上时，求证：①BD⊥CE，②CE=BC﹣CD；‎ ‎（2）如图2，当点D在线段BC的延长线上时，其他条件不变，请直接写出CE、BC、CD三条线段之间的关系；‎ ‎（3）如图3，当点O在线段BC的反向延长线上时，且点A、E分别在直线BC的两侧，点F是DE的中点，连接AF、CF，其他条件不变，请判断△ACF的形状，并说明理由．‎ ‎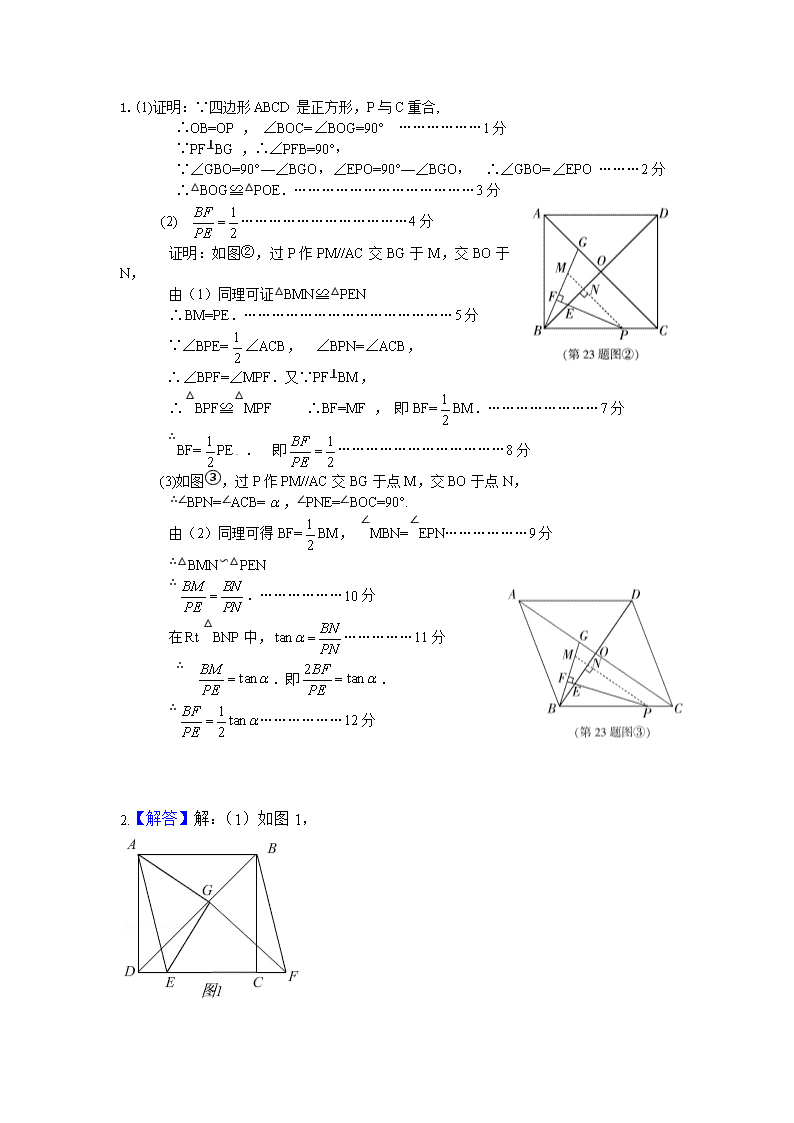1.(1)证明：∵四边形ABCD是正方形，P与C重合,‎ ‎∴OB=OP ， ∠BOC=∠BOG=90° ………………1分 ‎∵PF⊥BG ，∴∠PFB=90°，‎ ‎∵∠GBO=90°—∠BGO，∠EPO=90°—∠BGO， ∴∠GBO=∠EPO ………2分 ‎∴△BOG≌△POE．…………………………………3分 ‎(2)………………………………4分 证明：如图②，过P作PM//AC交BG于M，交BO于N，‎ 由（1）同理可证△BMN≌△PEN ‎ ‎∴BM=PE．………………………………………5分 ‎∵∠BPE=∠ACB， ∠BPN=∠ACB，‎ ‎∴∠BPF=∠MPF．又∵PF⊥BM，‎ ‎∴△BPF≌△MPF ∴BF=MF ， 即BF=BM．……………………7分 ‎∴BF=PE ． 即………………………………8分 ‎(3)如图③，过P作PM//AC交BG于点M，交BO于点N，‎ ‎∴∠BPN=∠ACB=，∠PNE=∠BOC=90°. ‎ 由（2）同理可得BF=BM， ∠MBN=∠EPN………………9分源:学科网ZXXK]‎ ‎∴△BMN∽△PEN ‎ ‎∴．………………10分 在△BNP中，……………11分 ‎ ‎∴．即．‎ ‎∴………………12分 ‎2.【解答】解：（1）如图1，‎ 由平移得，EF=AD，‎ ‎∵BD是正方形的对角线，‎ ‎∴∠ADB=∠CDB=45°，‎ ‎∵GF⊥BD，‎ ‎∴∠DGF=90°，‎ ‎∴∠GFD+∠CBD=90°，‎ ‎∴∠DFG=45°，‎ ‎∴GD=GF，‎ 在△AGD和△EGF中，‎ ‎，‎ ‎∴△AGD≌△EGF ‎∴AG=EG，∠AGD=∠EGF，‎ ‎∴∠AGE=∠AGD+∠DGE=∠EGF+DGE=90°，‎ ‎∴AG⊥EG．‎ 故答案为AG=EG，AG⊥EG．‎ ‎（2）（1）中的结论仍然成立，‎ 证明：如图2‎ 由平移得，EF=AD，‎ ‎∵BD是正方形的对角线，‎ ‎∴∠ADB=∠CDB=45°，‎ ‎∵GF⊥BD，‎ ‎∴∠DGF=90°，‎ ‎∴∠GFD+∠CBD=90°，‎ ‎∴∠DFG=45°，‎ ‎∴GD=GF，‎ 在△AGD和△EGF中，‎ ‎，‎ ‎∴△AGD≌△EGF ‎∴AG=EG，∠AGD=∠EGF，‎ ‎∴∠AGE=∠AGD+∠DGE=∠EGF+DGE=90°，‎ ‎∴AG⊥EG．‎ ‎（3）由（1）有，AG=CG，AG⊥EG，‎ ‎∴∠GEA=45°，‎ ‎∵∠AGF=120°，‎ ‎∴∠AGB=∠CGB，=30°，‎ ‎∴∠FGE=∠CGB=∠CGE=30°，‎ ‎∴∠CEG=75°，‎ ‎∴∠AED=30°，‎ 在Rt△ADE中，AD=2，‎ ‎∴DE=2．‎ ‎　‎ ‎3.【解答】（1）证明：如图1中，∵∠BAC=∠DAE=90°，‎ ‎∴∠BAD=∠CAE，‎ 在△ABD和△ACE中，‎ ‎，‎ ‎∴△ABD≌△ACE，‎ ‎∴∠ABD=∠ACE=45°，BD=CE，‎ ‎∴∠ACB+∠ACE=90°‎ ‎∴∠ECB=90°，‎ ‎∴BD⊥CE，CE=BC﹣CD．‎ ‎（2）如图2中，结论：CE=BC+CD，理由如下：‎ ‎∵∠BAC=∠DAE=90°，‎ ‎∴∠BAD=∠CAE，‎ 在△ABD和△ACE中，‎ ‎，‎ ‎∴△ABD≌△ACE，‎ ‎∴BD=CE，‎ ‎∴CE=BC+CD．‎ ‎（3）如图3中，结论：△ACF是等腰三角形．理由如下：‎ ‎∵∠BAC=∠DAE=90°，‎ ‎∴∠BAD=∠CAE，‎ 在△ABD和△ACE中，‎ ‎∴△ABD≌△ACE，‎ ‎∴∠ABD=∠ACE，‎ ‎∵∠ABC=∠ACB=45°，‎ ‎∴∠ACE=∠ABD=135°，‎ ‎∴∠DCE=90°，‎ 又∵点F是DE中点，‎ ‎∴AF=CF=DE，‎ ‎∴△ACF是等腰三角形．‎