江苏市中考数学压轴题汇编有答案 71页

江苏13市2012年中考数学试题分类解析汇编 专题12：押轴题 一、选择题 ‎1. （2012江苏常州2分）已知a、b、c、d都是正实数，且，给出下列四个不等式：‎ ‎ ①；②；③；④。‎ ‎ 其中不等式正确的是【 】‎ A. ①③ B. ①④ C. ②④ D. ②③‎ ‎【答案】A。‎ ‎【考点】不等式的性质。‎ ‎【分析】根据不等式的性质，计算后作出判断：‎ ‎ ∵a、b、c、d都是正实数，且，∴，即。‎ ‎ ∴，即，∴③正确，④不正确。‎ ‎∵a、b、c、d都是正实数，且，∴。∴，即。‎ ‎∴。∴①正确，②不正确。‎ ‎∴不等式正确的是①③。故选A。‎ ‎2. （2012江苏淮安3分）下列说法正确的是【 】‎ A、两名同学5次成绩的平均分相同，则方差较大的同学成绩更稳定。‎ B、某班选出两名同学参加校演讲比赛，结果一定是一名男生和一名女生 C、学校气象小组预报明天下雨的概率为0.8，则明天下雨的可能性较大 D、为了解我市学校“阳光体育”活动开展情况，必须采用普查的方法 ‎【答案】C。‎ ‎【考点】方差的意义，概率的意义，调查方法的选择。‎ ‎【分析】根据方差的意义，概率的意义，调查方法的选择逐一作出判断：‎ A、两名同学5次成绩的平均分相同，则方差较小的同学成绩更稳定，故本选项错误；‎ B、某班选出两名同学参加校演讲比赛，结果不一定是一名男生和一名女生，故本选项错误；‎ C、学校气象小组预报明天下雨的概率为0.8，则明天下雨的可能性较大，故本选项正确；‎ D、为了解我市学校“阳光体育”活动开展情况，易采用抽样调查的方法，故本选项错误。‎ 故选C。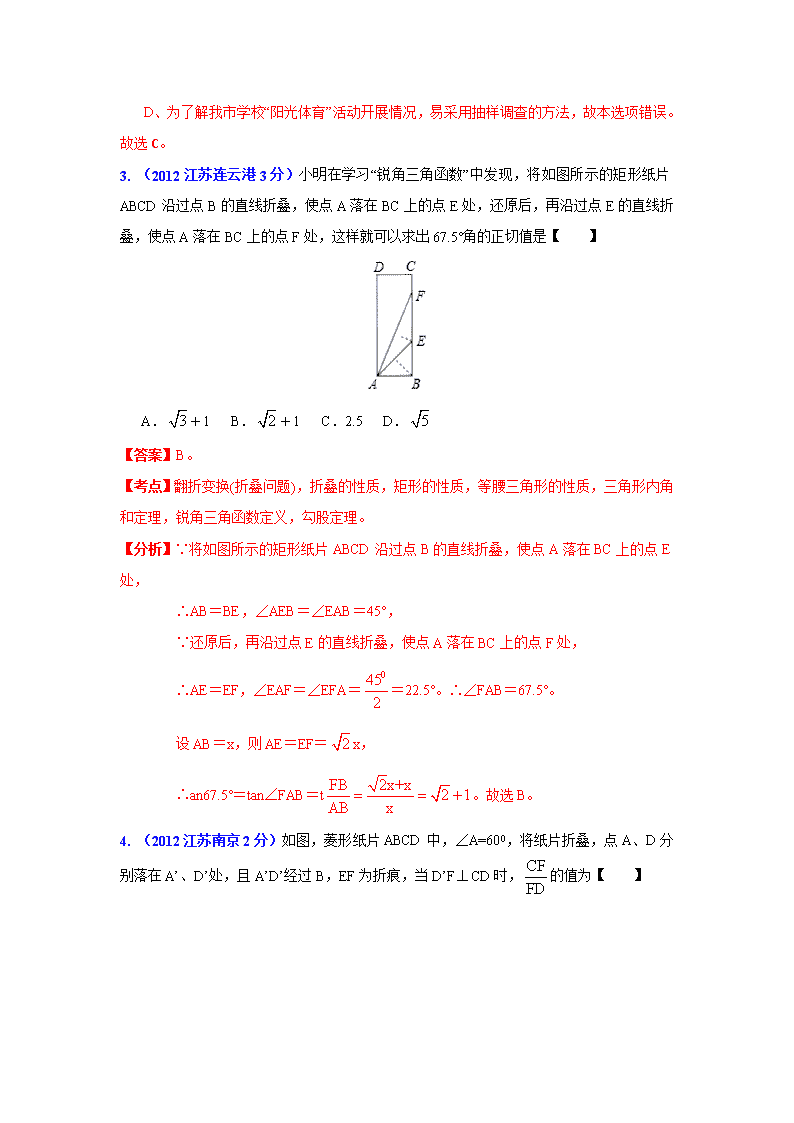‎ ‎3. （2012江苏连云港3分）小明在学习“锐角三角函数”中发现，将如图所示的矩形纸片ABCD沿过点B的直线折叠，使点A落在BC上的点E处，还原后，再沿过点E的直线折叠，使点A落在BC上的点F处，这样就可以求出67.5°角的正切值是【 】‎ A．＋1 B．＋‎1 ‎‎ C．2.5 D．‎ ‎【答案】B。‎ ‎【考点】翻折变换(折叠问题)，折叠的性质，矩形的性质，等腰三角形的性质，三角形内角和定理，锐角三角函数定义，勾股定理。‎ ‎【分析】∵将如图所示的矩形纸片ABCD沿过点B的直线折叠，使点A落在BC上的点E处，‎ ‎∴AB＝BE，∠AEB＝∠EAB＝45°，‎ ‎∵还原后，再沿过点E的直线折叠，使点A落在BC上的点F处，‎ ‎∴AE＝EF，∠EAF＝∠EFA＝＝22.5°。∴∠FAB＝67.5°。‎ 设AB＝x，则AE＝EF＝x，‎ ‎∴an67.5°＝tan∠FAB＝t。故选B。‎ ‎4. （2012江苏南京2分）如图，菱形纸片ABCD中，∠A=600，将纸片折叠，点A、D分别落在A’、D’处，且A’D’经过B，EF为折痕，当D’FCD时，的值为【 】‎ A. B. C. D. ‎ ‎【答案】A。‎ ‎【考点】翻折变换（折叠问题），菱形的性质，平行的性质，折叠的性质，锐角三角函数定义，特殊角的三角函数值。‎ ‎【分析】延长DC与A′D′，交于点M，‎ ‎∵在菱形纸片ABCD中，∠A=60°，‎ ‎∴∠DCB=∠A=60°，AB∥CD。‎ ‎∴∠D=180°-∠A=120°。‎ 根据折叠的性质，可得 ‎∠A′D′F=∠D=120°，‎ ‎∴∠FD′M=180°-∠A′D′F=60°。‎ ‎∵D′F⊥CD，∴∠D′FM=90°，∠M=90°-∠FD′M=30°。‎ ‎∵∠BCM=180°-∠BCD=120°，∴∠CBM=180°-∠BCM-∠M=30°。∴∠CBM=∠M。‎ ‎∴BC=CM。‎ 设CF=x，D′F=DF=y， 则BC=CM=CD=CF+DF=x+y。∴FM=CM+CF=2x+y，‎ 在Rt△D′FM中，tan∠M=tan30°=，∴。‎ ‎∴。故选A。‎ ‎5. （2012江苏南通3分）如图，在△ABC中，∠ACB＝90º，∠B＝30º，AC＝1，AC在直线l上．将△ABC 绕点A顺时针旋转到位置①，可得到点P1，此时AP1＝2；将位置①的三角形绕点P1顺时针旋转到位置②，‎ 可得到点P2，此时AP2＝2＋；将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3，此时AP3‎ ‎＝3＋；…，按此规律继续旋转，直到得到点P2012为止，则AP2012＝【 】‎ A．2011＋671 B．2012＋‎671 ‎ C．2013＋671 D．2014＋671 ‎【答案】B。‎ ‎【考点】分类归纳（图形的变化类），旋转的性质，锐角三角函数，特殊角的三角函数值。‎ ‎【分析】寻找规律，发现将Rt△ABC绕点A，P1，P2，···顺时针旋转，每旋转一次， APi（i=1,2,3,···）‎ 的长度依次增加2， ，1，且三次一循环，按此规律即可求解：‎ ‎ ∵Rt△ABC中，∠ACB=90°，∠B=30°，AC=1，∴AB=2，BC=。‎ 根据旋转的性质，将Rt△ABC绕点A，P1，P2，···顺时针旋转，每旋转一次， APi（i=1,2,3,···）‎ 的长度依次增加2， ，1，且三次一循环。‎ ‎ ∵2012÷3==670…2，‎ ‎∴AP2012=670（3+ ）+2+ =2012+671 。故选B。‎ ‎6. （2012江苏苏州3分）已知在平面直角坐标系中放置了5个如图所示的正方形（用阴影表示），点 B1在y轴上，点C1、E1、E2、C2、E3、E4、C3在x轴上．若正方形A1B‎1C1D1的边长为1，∠B‎1C1O=60°，‎ B‎1C1∥B‎2C2∥B‎3C3，则点A3到x轴的距离是【 】‎ A. B. C. D. ‎ ‎【答案】D。‎ ‎【考点】正方形的性质，平行的性质，三角形内角和定理，解直角三角形，锐角三角函数定义，特殊角的三角函数值。‎ ‎【分析】过小正方形的一个顶点W作FQ⊥x轴于点Q，过点A‎3F⊥FQ于点F，‎ ‎∵正方形A1B‎1C1D1的边长为1，∠B‎1C1O=60°，B‎1C1∥B‎2C2∥B‎3C3，‎ ‎∴∠B‎3C3 E4=60°，∠D‎1C1E1=30°，‎ ‎∠E2B‎2C2=30°。‎ ‎∴D1E1=D‎1C1=。‎ ‎∴D1E1=B2E2=。‎ ‎∴。‎ 解得：B‎2C2=。‎ ‎∴B3E4=。∴，解得：B‎3C3=。∴WC3=。‎ 根据题意得出：∠WC3 Q=30°，∠C3 WQ=60°，∠A3 WF=30°，‎ ‎∴WQ=，FW=WA3•cos30°=。‎ ‎∴点A3到x轴的距离为：FW+WQ=。故选D。‎ ‎7. （2012江苏宿迁3分）在平面直角坐标系中，若将抛物线y=2x2 - 4x+3先向右平移3个单位长度，再 向上平移2个单位长度，则经过这两次平移后所得抛物线的顶点坐标是【 】‎ A.（－2，3） B.（－1，4） C.（1，4） D.（4，3）‎ ‎【答案】D。‎ ‎【考点】坐标平移。‎ ‎【分析】‎ 根据坐标的平移变化的规律，左右平移只改变点的横坐标，左减右加。上下平移只改变点的纵坐标，下减上加。因此，将抛物线y=2x2 - 4x+3先向右平移3个单位长度，再向上平移2个单位长度，其顶点也同样变换。‎ ‎ ∵的顶点坐标是（1，1），‎ ‎ ∴点（1，1）先向右平移3个单位长度，再向上平移2个单位长度，得点（4，3），即经过这两次平移后所得抛物线的顶点坐标是（4，3）。故选D。‎ ‎8. （2012江苏泰州3分）下列四个命题：①一组对边平行且一组对角相等的四边形是平行四边形；②对 角线互相垂直且相等的四边形是正方形；③顺次连结矩形四边中点得到的四边形是菱形；④正五边形既是 轴对称图形又是中心对称图形．其中真命题共有【 】‎ A．1个 B．2个 C．3个 D．4个 ‎【答案】B。‎ ‎【考点】真假命题，平行四边形的判定，正方形的判定，菱形的判定，轴对称图形和中心对称图形。‎ ‎【分析】根据平行四边形的判定，正方形的判定，菱形的判定和轴对称图形、中心对称图形的概念逐一作出判断：‎ ‎①如图，四边形ABCD中，AD∥BC，∠ADC=∠ABC，‎ 连接BD，则 ‎∵AD∥BC，∴∠ADB=∠DBC（两直线平行，内错角相等）。‎ 又∵∠ADC=∠ABC，∴∠BDC=∠ABD（等量减等量，差相等）。‎ ‎∴AB∥DC（内错角相等，两直线平行）。‎ ‎∴四边形ABCD是平行四边形（平行四边形定义）。因此命题①正确。‎ ‎ ②举反例说明，如图，铮形对角线互相垂直且相等。因此命题②错误。‎ ‎ ③如图，矩形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点，‎ ‎ 连接AC，BD。‎ ‎ ∵E、F、G、H分别是AB、BC、CD、DA的中点，‎ ‎ ∴EF=AC，HG=AC，EF=BD，FG=BD（三角形中位线定理）。‎ ‎ 又∵矩形ABCD，∴AC=BD（矩形的对角线相等）。‎ ‎ ∴EF=HG=EF=FG（等量代换）。‎ ‎∴四边形EFGH是菱形（四边相等的辊边形是菱形）。因此命题③正确。‎ ‎④根据轴对称图形和中心对称图形的概念，正五边形是轴对称图形，不是中心对称图形。因此命题④错误。‎ ‎ 综上所述，正确的命题即真命题有①③。故选B。‎ ‎9. （2012江苏无锡3分）如图，以M（﹣5，0）为圆心、4为半径的圆与x轴交于A．B两点，P是⊙M上异于A．B的一动点，直线PA．PB分别交y轴于C．D，以CD为直径的⊙N与x轴交于E、F，则EF的长【 】‎ ‎　 A． 等于4 B． 等于‎4‎ C． 等于6 D． 随P点 ‎【答案】C。‎ ‎【考点】圆周角定理，三角形内角和定理，相似三角形的判定和性质，垂径定理，勾股定理。‎ ‎【分析】 连接NE，设圆N半径为r，ON=x，则OD=r﹣x，OC=r+x，‎ ‎∵以M（﹣5，0）为圆心、4为半径的圆与x轴交于A．B两点，‎ ‎∴OA=4+5=9，0B=5﹣4=1。‎ ‎∵AB是⊙M的直径，∴∠APB=90°。‎ ‎∵∠BOD=90°，∴∠PAB+∠PBA=90°，∠ODB+∠OBD=90°。‎ ‎∵∠PBA=∠OBD，∴∠PAB=∠ODB。‎ ‎∵∠APB=∠BOD=90°，∴△OBD∽△OCA。∴，即，即r2﹣x2=9。‎ 由垂径定理得：OE=OF，‎ 由勾股定理得：OE2=EN2﹣ON2=r2﹣x2=9。∴OE=OF=3，∴EF=2OE=6。‎ 故选C。‎ ‎10. （2012江苏徐州3分）如图，在正方形ABCD中，E是CD的中点，点F在BC上，且FC=BC。图中相似三角形共有【 】‎ A．1对 B．2对 C．3对 D．4对 ‎【答案】C。‎ ‎【考点】正方形的性质，勾股定理，相似三角形的判定。‎ ‎【分析】根据正方形的性质，求出各边长，应用相似三角形的判定定理进行判定： ‎ ‎ 同已知，设CF=a，则CE=DE=‎2a，AB=BC=CD=DA=‎4a，BF=‎3a。‎ ‎ 根据勾股定理，得EF=，AE=，AF=‎5a。‎ ‎ ∴。‎ ‎∴△CEF∽△DEA，△CEF∽△EAF，△DEA∽△EAF。共有3对相似三角形。故选C。‎ ‎11. （2012江苏盐城3分）已知整数满足下列条件：,,, ‎ ‎,…,依次类推，则的值为【 】‎ ‎ A． B． C． D．‎ ‎【答案】B。‎ ‎【考点】分类归纳（数字的变化类）‎ ‎【分析】根据条件求出前几个数的值，寻找规律，分是奇数和偶数讨论：：‎ ‎ ∵， ，‎ ‎，，‎ ‎，，‎ ‎，，‎ ‎…，‎ ‎∴当是奇数时，，是偶数时， 。‎ ‎∴。故选B。‎ ‎12. （2012江苏扬州3分）大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和，如23＝3＋5，33＝7＋9＋11，43＝13＋15＋17＋19，…若m3分裂后，其中有一个奇数是2013，则m的值是【 】‎ A．43 B．‎44 ‎‎ C．45 D．46‎ ‎【答案】C。‎ ‎【考点】分类归纳（数字的变化类）。‎ ‎【分析】分析规律，然后找出2013所在的奇数的范围，即可得解：‎ ‎∵23＝3＋5，33＝7＋9＋11，43＝13＋15＋17＋19，‎ ‎…‎ ‎∴m3分裂后的第一个数是m(m－1)＋1，共有m个奇数。‎ ‎∵45×(45－1)＋1＝1981，46×(46－1)＋1＝2071，‎ ‎∴第2013个奇数是底数为45的数的立方分裂后的一个奇数，‎ ‎∴m＝45。故选C。‎ ‎13. （2012江苏镇江3分）边长为a的等边三角形，记为第1个等边三角形。取其各边的三等分点，顺次连接得到一个正六边形，记为第1个正六边形。取这个正六边形不相邻的三边中点顺次连接，又得到一个等边三角形，记为第2个等边三角形。取其各边的三等分点，顺次连接又得到一个正六边形，记为第2个正六边形（如图）…，按此方式依次操作。则第6个正六边形的边长是【 】‎ A. B. C. D. ‎ ‎【答案】A。‎ ‎【考点】分类归纳（图形的变化类），等边三角形和判定和性质，三角形中位线定理。‎ ‎【分析】如图，双向延长EF分别交AB、AC于点G、H。‎ ‎ 根据三角形中位线定理，得GE=FH=，GB=CH=。‎ ‎ ∴AG=AH=。‎ ‎ 又∵△ABC中，∠A=600，∴△AGH是等边三角形。‎ ‎ ∴GH=AG=AH=。EF= GH－GE－FH=。‎ ‎ ∴第2个等边三角形的边长为。‎ ‎ 同理，第3个等边三角形的边长为，第4个等边三角形的边长为，第5个等边三角形的边长为，第6个等边三角形的边长为。‎ ‎ 又∵相应正六边形的边长是等边三角形的边长的，‎ ‎ ∴第6个正六边形的边长是。故选A。‎ 二、填空题 ‎1. （2012江苏常州2分）如图，已知反比例函数和。点A在y轴的正半轴上，过点A作直线BC∥x轴，且分别与两个反比例函数的图象交于点B和C，连接OC、OB。若△BOC的面积为，AC：AB=2：3，则= ▲ ，= ▲ 。‎ ‎2. （2012江苏淮安3分）如图，射线OA、BA分别表示甲、乙两人骑自行车运动过程的一次函数的图象，图中s、t分别表示行驶距离和时间，则这两人骑自行车的速度相差 ▲ km/h。‎ ‎【答案】4。‎ ‎【考点】一次函数的图象和应用。‎ ‎【分析】要求这两人骑自行车的速度相差，只要由图象求出两人5 h行驶的距离即可：‎ ‎ 甲5 h行驶的距离为‎100 km，故速度为100÷5=‎20 km/h；‎ 乙5 h行驶的距离为‎100 km－‎20km =‎80 km，故速度为80÷5=‎16 km/h。‎ ‎∴这两人骑自行车的速度相差20－16=‎4 km/h。‎ ‎3. （2012江苏连云港3分）如图，直线y＝k1x＋b与双曲线交于A、B两点，其横坐标分别为1和5，则不等式k1x＜＋b的解集是　▲　．‎ ‎【答案】－5＜x＜－1或x＞0。‎ ‎【考点】不等式的图象解法，平移的性质，反比例函数与一次函数的交点问题，对称的性质。‎ ‎【分析】不等式k1x＜＋b的解集即k1x－b＜的解集，根据不等式与直线和双曲线解析式的关系，可以理解为直线y＝k1x－b在双曲线下方的自变量x的取值范围即可。‎ 而直线y＝k1x－b的图象可以由y＝k1x＋b向下平移2b个单位得到，如图所示。根据函数图象的对称性可得：直线y＝k1x－b和y＝k1x＋b与双曲线的交点坐标关于原点对称。‎ 由关于原点对称的坐标点性质，直线y＝k1x－b图象与双曲线图象交点A′、B′的横坐标为A、B两点横坐标的相反数，即为－1，－5。‎ ‎∴由图知，当－5＜x＜－1或x＞0时，直线y＝k1x－b图象在双曲线图象下方。‎ ‎∴不等式k1x＜＋b的解集是－5＜x＜－1或x＞0。‎ ‎4. （2012江苏南京2分）在平面直角坐标系中，规定把一个三角形先沿x轴翻折，再向右平移两个单位称为一次变换，如图，已知等边三角形ABC的顶点B、C的坐标分别是，（-1，-1），（-3，-1），把三角形ABC经过连续9次这样的变换得到三角形A’B’C’，则点A的对应点A’的坐标是 ▲ ‎ ‎【答案】（16，）。‎ ‎【考点】分类归纳（图形的变化类），翻折变换（折叠问题），坐标与图形性质，等边三角形的性质，锐角三角函数定义，特殊角的三角函数值。‎ ‎【分析】先由△ABC是等边三角形，点B、C的坐标分别是（－1，1）、（－3，－1），求得点A的坐标；再寻找规律，求出点A的对应点A′的坐标：‎ ‎ 如图，作BC的中垂线交BC于点D，则 ‎ ∵△ABC是等边三角形，点B、C的坐标分别是（－1，1）、（－3，－1），‎ ‎ ∴BD=1，。∴A（—2，）。‎ ‎ 根据题意，可得规律：第n次变换后的点A的对应点的坐标：当n为奇数时为（2n－2，），当n为偶数时为（2n－2， ）。‎ ‎ ∴把△ABC经过连续9次这样的变换得到△A′B′C′，则点A的对应点A′的坐标是：（16，）。‎ ‎5. （2012江苏南通3分）无论a取什么实数，点P(a－1，‎2a－3)都在直线l上，Q(m，n)是直线l上的点，‎ 则(‎2m－n＋3)2的值等于 ▲ ．‎ ‎【答案】16。‎ ‎【考点】待定系数法，直线上点的坐标与方程的关系，求代数式的值。‎ ‎【分析】∵由于a不论为何值此点均在直线l上，‎ ‎∴令a=0，则P1（－1，－3）；再令a=1，则P2（0，－1）。‎ 设直线l的解析式为y=kx+b（k≠0），‎ ‎∴ ，解得 。‎ ‎∴直线l的解析式为：y=2x－1。‎ ‎∵Q（m，n）是直线l上的点，∴‎2m－1=n，即‎2m－n=1。‎ ‎∴(‎2m－n＋3)2=（1+3）2=16。‎ ‎6. （2012江苏苏州3分）如图①，在梯形ABCD中，AD∥BC，∠A=60°，动点P从A点出发，以‎1cm/s 的速度沿着A→B→C→D的方向不停移动，直到点P到达点D后才停止.已知△PAD的面积S（单位：）‎ 与点P移动的时间t（单位：s）的函数关系式如图②所示，则点P从开始移动到停止移动一共用了 ▲ 秒 ‎（结果保留根号）.‎ ‎【答案】4＋。‎ ‎【考点】动点问题的函数图象，矩形的判定和性质，锐角三角函数定义，特殊角的三角函数值，勾股定理。‎ ‎【分析】由图②可知，t在2到4秒时，△PAD的面积不发生变化，‎ ‎∴在AB上运动的时间是2秒，在BC上运动的时间是4－2=2秒。‎ ‎∵动点P的运动速度是‎1cm/s，∴AB=2，BC=2。‎ 过点B作BE⊥AD于点E，过点C作CF⊥AD于点F，‎ 则四边形BCFE是矩形。∴BE=CF，BC=EF=2。‎ ‎∵∠A=60°，‎ ‎∴，。‎ ‎∵由图②可△ABD的面积为，‎ ‎∴，即， 解得AD=6。‎ ‎∴DF=AD－AE－EF=6－1－2=3。‎ 在Rt△CDF中，，‎ ‎∴动点P运动的总路程为AB＋BC＋CD=2＋2＋=4＋（cm）。‎ ‎∵动点P的运动速度是‎1cm/s，‎ ‎∴点P从开始移动到停止移动一共用了（4+）÷1=4+s。‎ ‎7. （2012江苏宿迁3分）按照如图所示的方法排列黑色小正方形地砖，则第14个图案中黑色小正方形地砖的块数是 ▲ .‎ ‎【答案】365。‎ ‎【考点】分类归纳（图形的变化类）。寻找规律，‎ ‎【分析】画树状图：记第n个图案中黑色小正方形地砖的块数是an，则 ‎ ∴an－an－1=4（n－1）（n=2，3，4，···），‎ ‎ ∴（a2－a1）＋（a3－a2）＋（a4－a3）＋···＋（an－an－1）=4＋8＋···＋4（n－1），‎ ‎ 即an－a1=4[1＋2＋3＋···＋（n－1）]=‎ ‎ ∴an=＋a1=。‎ ‎ 当n=14时，a14 =。‎ ‎8. （2012江苏泰州3分）如图，在边长相同的小正方形组成的网格中，点A、B、C、D都在这 些小正方形的顶点上，AB、CD相交于点P，则tan∠APD的值是 ▲ ．‎ ‎【答案】2。‎ ‎【考点】正方形的性质，相似三角形的判定和性质，锐角三角函数的定义。‎ ‎【分析】如图，连接BE，交CD于点F。‎ ‎∵四边形BCED是正方形，‎ ‎∴DF=CF=CD，BF=BE，CD=BE，BE⊥CD，∴BF=CF。‎ 根据题意得：AC∥BD，∴△ACP∽△BDP。‎ ‎∴DP：CP=BD：AC=1：3。∴DP=PF=CF= BF。‎ 在Rt△PBF中，。‎ ‎∵∠APD=∠BPF，∴tan∠APD=2。‎ ‎9. （2012江苏无锡2分）如图的平面直角坐标系中有一个正六边形ABCDEF，其中C．D的坐标分别为（1，0）和（2，0）．若在无滑动的情况下，将这个六边形沿着x轴向右滚动，则在滚动过程中，这个六边形的顶点A．B．C．D．E、F中，会过点（45，2）的是点　 ▲ 　．‎ ‎【答案】B。‎ ‎【考点】分类归纳（图形的变化类），坐标与图形性质，正多边形和圆，旋转的性质。‎ ‎【分析】由正六边形ABCDEF中C．D的坐标分别为（1，0）和（2，0），得正六边形边长为1，周长为6。‎ ‎ ∴正六边形滚动一周等于6。如图所示。‎ 当正六边形ABCDEF滚动到位置1，2，3，4，5，6，7时，顶点A．B．C．D．E、F的纵坐标为2。‎ 位置1时，点A的横坐标也为2。‎ 又∵（45－2）÷6=7…1，‎ ‎∴恰好滚动7周多一个，即与位置2顶点的纵坐标相同，此点是点B。‎ ‎∴会过点（45，2）的是点B。‎ ‎10. （2012江苏徐州2分）函数的图象如图所示，关于该函数，下列结论正确的是 ▲ （填序号）。‎ ①函数图象是轴对称图形；②函数图象是中心对称图形；③当x>0时，函数有最小值；④点（1，4）在函数图象上；⑤当x＜1或x＞3时，y＞4。‎ ‎【答案】②③④。‎ ‎【考点】函数的图象和性质，轴对称图形和中心对称图形，曲线上点的坐标与方程的关系。‎ ‎【分析】根据图象作出判断：‎ ①函数图象不是轴对称图形。故结论①错误。‎ ②函数图象是中心对称图形，对称中心是坐标原点。故结论②正确。‎ ③∵当x>0时，，∴函数有最小值。故结论③正确。‎ ④∵当x=1时，。∴点（1，4）在函数图象上。故结论④正确。‎ ⑤∵当x＜0时，y＜0，∴当x＜1时，y不大于4。故结论⑤错误。‎ ‎∴结论正确的是②③④。‎ ‎11. （2012江苏盐城3分）一批志愿者组成了一个“爱心团队”,专门到全国各地巡回演出,以募集爱心基金.‎ 第一个月他们就募集到资金1万元,随着影响的扩大,第n（n≥2）个月他们募集到的资金都将会比上个月增 加20%,则当该月所募集到的资金首次突破10万元时,相应的n的值为 ▲ .‎ ‎(参考数据:,,)‎ ‎【答案】13。‎ ‎【考点】同底数幂的乘法 ‎【分析】第一个月募集到资金1万元，则由题意第二个月募集到资金（1+20%）万元，第三个月募集到资 金（1+20%）2万元，…，第n个月募集到资金（1+20%）n-1万元，由题意得：‎ ‎ （1+20%）n－1＞10，即1.2 n－1＞10.‎ ‎∵1.25×1.26≈7.5＜10，1.25×1.27≈10.8＞10，‎ ‎∴n－1=5+7=12，解得，n=13。‎ ‎12. （2012江苏扬州3分）如图，双曲线经过Rt△OMN斜边上的点A，与直角边MN相交于点B，已知OA＝2AN，△OAB的面积为5，则k的值是　▲　．‎ ‎【答案】12。‎ ‎【考点】反比例函数综合题。‎ ‎【分析】如图，过A点作AC⊥x轴于点C，则AC∥NM，‎ ‎ ∴△OAC∽△ONM，∴OC：OM＝AC：NM＝OA：ON。‎ 又∵OA＝2AN，∴OA：ON＝2：3。‎ 设A点坐标为(x0，y0)，则OC＝x0，AC＝y0。‎ ‎∴OM＝，NM＝。∴N点坐标为(，)。‎ ‎∴点B的横坐标为，设B点的纵坐标为yB，‎ ‎∵点A与点B都在图象上，∴k＝x0 •y0＝•yB。∴。‎ ‎∴B点坐标为()。‎ ‎∵OA＝2AN，△OAB的面积为5，∴△NAB的面积为。∴△ONB的面积＝。‎ ‎∴，即。∴。∴k＝12。‎ ‎13. （2012江苏镇江2分）如图，在平面直角坐标系x0y中，直线AB过点A（－4，0），B（0，4），⊙O的半径为1（O为坐标原点），点P在直线AB上，过点P作⊙O的一条切线PQ，Q为切点，则切线长PQ 的最小值为 ▲ 。‎ 三、解答题 ‎1. （2012江苏常州9分）已知，在矩形ABCD中，AB=4，BC=2，点M为边BC的中点，点P为边CD上的动点（点P异于C、D两点）。连接PM，过点P作PM的垂线与射线DA相交于点E（如图）。设CP=x，DE=y。‎ ‎（1）写出y与x之间的函数关系式 ▲ ；‎ ‎（2）若点E与点A重合，则x的值为 ▲ ；‎ ‎（3）是否存在点P，使得点D关于直线PE的对称点D′落在边AB上？若存在，求x的值；若不存在，请说明理由。‎ ‎【答案】解：（1）y=－x2＋4x。‎ ‎ （2）或。‎ ‎ （3）存在。‎ ‎ 过点P作PH⊥AB于点H。则 ‎ ∵点D关于直线PE的对称点D′落在边AB上，‎ ‎ ∴P D′=PD=4－x，E D′=ED= y=－x2＋4x，EA=AD－ED= x2－4x＋2，∠P D′E=∠D=900。‎ ‎ 在Rt△D′P H中，PH=2， D′P =DP=4－x，D′H=。‎ ‎ ∵∠ E D′A=1800－900－∠P D′H=900－∠P D′H=∠D′P H，∠P D′E=∠P HD′ =900，‎ ‎ ∴△E D′A∽△D′P H。∴，即，‎ ‎ 即，两边平方并整理得，2x2－4x＋1=0。解得。‎ ‎∵当时，y=，‎ ‎∴此时，点E已在边DA延长线上，不合题意，舍去（实际上是无理方程的增根）。‎ ‎∵当时，y=，‎ ‎∴此时，点E在边AD上，符合题意。‎ ‎∴当时，点D关于直线PE的对称点D′落在边AB上。‎ ‎【考点】矩形的性质，相似三角形的判定和性质，勾股定理，折叠对称的性质，解无理方程。‎ ‎【分析】（1）∵CM=1，CP=x，DE=y，DP=4－x，且△MCP∽△PDE，‎ ‎ ∴，即。∴y=－x2＋4x。‎ ‎（2）当点E与点A重合时，y=2，即2=－x2＋4x，x2－4x＋2=0。‎ ‎ 解得。‎ ‎（3）过点P作PH⊥AB于点H，则由点D关于直线PE的对称点D′落在边AB上，可得△E D′A与△D′P H相似，由对应边成比例得得关于x的方程即可求解。注意检验。‎ ‎2. （2012江苏常州10分）在平面直角坐标系xOy中，已知动点P在正比例函数y=x的图象上，点P的横坐标为m（m＞0）。以点P为圆心，为半径的圆交x轴于A、B两点（点A在点B的左侧），交y轴于C、D两点（D点在点C的上方）。点E为平行四边形DOPE的顶点（如图）。‎ ‎（1）写出点B、E的坐标（用含m的代数式表示）；‎ ‎（2）连接DB、BE，设△BDE的外接圆交y轴于点Q（点Q异于点D），连接EQ、BQ。试问线段BQ与线段EQ的长是否相等？为什么？‎ ‎（3）连接BC，求∠DBC－∠DBE的度数。‎ ‎【答案】解：（1）B（‎3m，0），E（m，‎4m）。‎ ‎（2）线段BQ与线段EQ的长相等。理由如下：‎ 由（1）知B（‎3m，0），E（m，‎4m），‎ ‎∵根据圆的对称性，点D点B关于y=x对称，‎ ‎∴D（0，‎3m）。‎ ‎∴，，‎ ‎。‎ ‎∴。∴△BDE是直角三角形。‎ ‎∴BE是△BDE的外接圆的直径。‎ 设△BDE的外接圆的圆心为点G，则由B（‎3m，0），E（m，‎4m）得G（‎2m，‎2m）。‎ 过点G作GI⊥DG于点I，则I（0，‎2m）。‎ 根据垂径定理，得DI=IQ ，∴Q（0，m）。‎ ‎∴。‎ ‎∴BQ=EQ。‎ ‎（3）延长EP交x轴于点H，则EP⊥AB，BH=‎2m。‎ 根据垂径定理，得AH=BH=‎2m，AO= m。‎ 根据圆的对称性，OC=OA= m。‎ 又∵OB=‎3m，，，‎ ‎∴。。‎ 又∵∠COB=∠EDB=900，∴△COB∽△EDB。∴∠OBC=∠DBE。‎ ‎∴∠DBC－∠DBE=∠DBC－∠OBC=∠DBO。‎ 又∵OB=OC，∴∠DBO=450。∴∠DBC－∠DBE=450。‎ ‎【考点】直线上点的坐标与方程的关系，勾股定理和逆定理，圆的对称性，平行四边形的性质，中点坐标，圆周角定理，垂径定理，等腰三角形的判定和性质，相似三角形的判定和性质。‎ ‎【分析】（1）过点P 作PH⊥x轴于点H，PF⊥y轴于点F，连接OE，BP。‎ ‎∵点P在正比例函数y=x的图象上，点P的横坐标为m（m＞0），‎ ‎∴ P（m，m），H（m，0），F（0，m），OH=OF=HP= m。‎ ‎∵PB=，∴。‎ ‎∴OB=‎3 m。∴B（‎3m，0）。‎ ‎∵根据圆的对称性，点D点B关于y=x对称，∴D（0，‎3m）。‎ ‎∵四边形DOPE是平行四边形，∴PE=OD=‎3m，HE=‎4m。∴E（m，‎4 m）。‎ ‎（2）由勾股定理和逆定理，易知△BDE是直角三角形，从而根据圆周角定理和垂径定理可得点Q的坐标，从而根据勾股定理可求出BQ和EQ的长比较即得。‎ ‎（3）求出有关线段的长，可得，从而证得△COB∽△EDB，得到∠OBC=∠DBE。因此∠DBC－∠DBE=∠DBC－∠OBC=∠DBO=450。‎ ‎3. （2012江苏淮安12分）如图，矩形OABC在平面直角坐标系中，O为坐标原点，点A（0，4），C（2，0），将矩形OABC绕点O按顺时针方向旋转1350，得到矩形EFGH（点E与O重合）.‎ ‎（1）若GH交y轴于点M，则∠FOM＝ ，OM= ‎ ‎（2）矩形EFGH沿y轴向上平移t个单位。‎ ‎①直线GH与x轴交于点D，若AD∥BO，求t的值；‎ ‎②若矩形EFHG与矩形OABC重叠部分的面积为S个平方单位，试求当0∠C）之间的等量关系。‎ 根据以上内容猜想：若经过n 次折叠∠BAC是△ABC的好角，则∠B与∠C不妨设∠B>∠C）之间的等量关系为 ‎ 应用提升 ‎（3）小丽找到一个三角形，三个角分别为150，600，1050，发现600和1050的两个角都是此三角形的好角，‎ 请你完成，如果一个三角形的最小角是40，试求出三角形另外两个角的度数，使该三角形的三个角均是此三角形的好角 ‎【答案】解：（1）是。 （2）∠B=3∠C。‎ 如图所示，在△ABC中，沿∠BAC的平 分线AB1折叠，剪掉重复部分；将余下部分沿∠B‎1A1C的平分线A1B2折叠，剪掉重复部分，将余下部分沿∠B‎2A2C的平分线A2B3折叠，点B2与点C重合，则∠BAC是△ABC的好角。‎ 证明如下：‎ ‎∵根据折叠的性质知，∠B=∠AA1B1，∠C=∠A2B‎2C，∠A1 B‎1C=∠A‎1A2B2，‎ ‎∴根据三角形的外角定理知，∠A‎1A2B2=∠C+∠A2B‎2C=2∠C。‎ ‎∵根据四边形的外角定理知，‎ ‎∠BAC+∠B+∠AA1B1－∠A1 B‎1C=∠BAC+2∠B－‎2C=180°，‎ 根据三角形ABC的内角和定理知，∠BAC+∠B+∠C=180°，‎ ‎∴∠B=3∠C。‎ 故若经过n次折叠∠BAC是△ABC的好角，则∠B与∠C（不妨设∠B＞∠C）之间的等量关系为∠B=n∠C。‎ ‎（3）由（2）知，∠B=n∠C，∠BAC是△ABC的好角，‎ ‎∴∠C=n∠A，∠ABC是△ABC的好角，∠A=n∠B，∠BCA是△ABC的好角。‎ ‎∴如果一个三角形的最小角是4°，三角形另外两个角的度数是88°、88°。‎ ‎【考点】分类归纳（图形的变化类），新定义，翻折变换（折叠问题），折叠的性质，三角形的内角和外角定理。‎ ‎【分析】（1）理由如下：小丽展示的情形二中，如图3，‎ ‎∵沿∠BAC的平分线AB1折叠，∴∠B=∠AA1B1。‎ 又∵将余下部分沿∠B‎1A1C的平分线A1B2折叠，此时点B1与点C重合，∴∠A1B‎1C=∠C。∵∠AA1B1=∠C+∠A1B‎1C（外角定理），∴∠B=2∠C。故答案是。‎ ‎（2）根据折叠的性质、根据三角形的外角定理知∠A‎1A2B2=∠C+∠A2B‎2C=2∠C；根据四边形的外角定理知∠BAC+2∠B－‎2C=180°①，根据三角形ABC的内角和定理知∠BAC+∠B+∠C=180°②，由①②可以求得∠B=3∠C。‎ 由小丽展示的情形一知，当∠B=∠C时，∠BAC是△ABC的好角；‎ 由小丽展示的情形二知，当∠B=2∠C时，∠BAC是△ABC的好角；‎ 由小丽展示的情形三知，当∠B=3∠C时，∠BAC是△ABC的好角；‎ 利用数学归纳法，根据小丽展示的三种情形得出结论：∠B=n∠C。‎ ‎（3）利用（2）的结论知∠B=n∠C，∠BAC是△ABC的好角，∠C=n∠A，∠ABC是△ABC的好角，∠A=n∠B，∠BCA是△ABC的好角，然后三角形内角和定理可求得另外两个角的度数可以是88°、88°。‎ ‎5. （2012江苏连云港12分）如图，甲、乙两人分别从A(1，)、B(6，0)两点同时出发，点O为坐标原点，甲沿AO方向、乙沿BO方向均以‎4km/h的速度行驶，th后，甲到达M点，乙到达N点．‎ ‎(1)请说明甲、乙两人到达O点前，MN与AB不可能平行．‎ ‎(2)当t为何值时，△OMN∽△OBA？‎ ‎(3)甲、乙两人之间的距离为MN的长，设s＝MN2，求s与t之间的函数关系式，并求甲、乙两人之间距离的最小值．‎ ‎【答案】解：(1)∵A坐标为(1，)，∴OA＝2，∠AOB＝60°。‎ ‎ ∵甲达到O点时间为t＝，乙达到O点的时间为t＝，‎ ‎∴甲先到达O点，所以t＝或t＝时，O、M、N三点不能连接成三角形。‎ ‎①当t＜时，OM＝2－4t，ON＝6－4t，‎ 假设MN∥AB。则△OMN∽△OAB。‎ ‎∴，解得t＝0。即在甲到达O点前，只有当t＝0时，△OMN∽△OAB。‎ ‎∴MN与AB不可能平行。‎ ‎②当＜t＜时，‎ 如图，∵∠PMN＞∠PON＞∠PAB ‎∴MN与AB不平行。‎ 综上所述，在甲、乙两人到达O点前， MN与AB不可能平行。‎ ‎(2) 由（1）知，当t≤时，△OMN不相似△OBA。‎ 当t＞时，OM＝4t －2，ON＝4t －6，‎ 由解得t＝2＞，‎ ‎∴当t＝2时，△OMN∽△OBA。‎ ‎(3)①当t≤时，如图1，过点M作MH⊥x轴，垂足为H，‎ 在Rt△MOH中，∵∠AOB＝60°，‎ ‎∴MH＝OMsin60°＝(2－4t)×＝(1－2t)，‎ OH＝0Mcos60°＝(2－4t)×＝1－2t，‎ ‎∴NH＝(6－4t)－(1－2t)＝5－2t。‎ ‎∴s＝[(1－2t)]2＋(5－2t)2＝16t2－32t＋28。‎ ‎②当＜t≤时，如图2，作MH⊥x轴，垂足为H，‎ 在Rt△MNH中，MH＝(4t－2)＝(2t－1)，‎ NH＝(4t－2)＋(6－4t)＝5－2t，‎ ‎∴s＝[(1－2t)]2＋(5－2t)2＝16t2－32t＋28。‎ ③当t＞时，同理可得s＝16t2－32t＋28。‎ 综上所述，s＝16t2－32t＋28。‎ ‎∵s＝16t2－32t＋28＝16(t－1)2＋12，‎ ‎∴当t＝1时，s有最小值为12，‎ ‎∴甲、乙两人距离最小值为（km）。‎ ‎【考点】反证法，坐标与图形性质，平行的判定和性质，相似三角形的判定和性质，三角形外角性质，勾股定理，锐角三角函数定义，特殊角的三角函数值，二次函数的最值。‎ ‎【分析】(1)用反证法说明．根据已知条件分别表示相关线段的长度，根据三角形相似得比例式说明。‎ ‎(2)根据两个点到达O点的时间不同分段讨论解答。‎ ‎(3)在不同的时间段运用相似三角形的判定和性质分别求解析式，运用函数性质解答问题。‎ ‎6. （2012江苏连云港12分）已知梯形ABCD，AD∥BC，AB⊥BC，AD＝1，AB＝2，BC＝3，‎ 问题1：如图1，P为AB边上的一点，以PD，PC为边作平行四边形PCQD，请问对角线PQ，DC的长能否相等，为什么？‎ 问题2：如图2，若P为AB边上一点，以PD，PC为边作平行四边形PCQD，请问对角线PQ的长是否存在最小值？如果存在，请求出最小值，如果不存在，请说明理由．‎ 问题3：若P为AB边上任意一点，延长PD到E，使DE＝PD，再以PE，PC为边作平行四边形PCQE，请探究对角线PQ的长是否也存在最小值？如果存在，请求出最小值，如果不存在，请说明理由．‎ 问题4：如图3，若P为DC边上任意一点，延长PA到E，使AE＝nPA(n为常数)，以PE、PB为边作平行四边形PBQE，请探究对角线PQ的长是否也存在最小值？如果存在，请求出最小值，如果不存在，请说明理由．‎ ‎【答案】解：问题1：对角线PQ与DC不可能相等。理由如下：‎ ‎∵四边形PCQD是平行四边形，若对角线PQ、DC相等，则四边形PCQD是矩形，‎ ‎∴∠DPC＝90°。‎ ‎∵AD＝1，AB＝2，BC＝3，∴DC＝2。‎ 设PB＝x，则AP＝2－x，‎ 在Rt△DPC中，PD2＋PC2＝DC2，即x2＋32＋(2－x)2＋12＝8，化简得x2－2x＋3＝0，‎ ‎∵△＝(－2)2－4×1×3＝－8＜0，∴方程无解。‎ ‎∴不存在PB＝x，使∠DPC＝90°。∴对角线PQ与DC不可能相等。‎ 问题2：存在。理由如下：‎ 如图2，在平行四边形PCQD中，设对角线PQ与DC相交于点G，‎ 则G是DC的中点。‎ 过点Q作QH⊥BC，交BC的延长线于H。‎ ‎∵AD∥BC，∴∠ADC＝∠DCH，即∠ADP＋∠PDG＝∠DCQ＋∠QCH。‎ ‎∵PD∥CQ，∴∠PDC＝∠DCQ。∴∠ADP＝∠QCH。‎ 又∵PD＝CQ，∴Rt△ADP≌Rt△HCQ（AAS）。∴AD＝HC。‎ ‎∵AD＝1，BC＝3，∴BH＝4，‎ ‎∴当PQ⊥AB时，PQ的长最小，即为4。‎ 问题3：存在。理由如下：‎ 如图3，设PQ与DC相交于点G，‎ ‎∵PE∥CQ，PD＝DE，∴。‎ ‎∴G是DC上一定点。‎ 作QH⊥BC，交BC的延长线于H，‎ 同理可证∠ADP＝∠QCH，∴Rt△ADP∽Rt△HCQ。∴。‎ ‎∵AD＝1，∴CH＝2。∴BH＝BG＋CH＝3＋2＝5。‎ ‎∴当PQ⊥AB时，PQ的长最小，即为5。‎ 问题4：如图3，设PQ与AB相交于点G，‎ ‎∵PE∥BQ，AE＝nPA，∴。‎ ‎∴G是DC上一定点。‎ 作QH∥PE，交CB的延长线于H，过点C作CK⊥CD，交QH 的延长线于K。‎ ‎∵AD∥BC，AB⊥BC，‎ ‎∴∠D＝∠QHC，∠DAP＋∠PAG＝∠QBH＋∠QBG＝90°‎ ‎∠PAG＝∠QBG，‎ ‎∴∠QBH＝∠PAD。∴△ADP∽△BHQ，∴，‎ ‎∵AD＝1，∴BH＝n＋1。∴CH＝BH＋BC＝3＋n＋1＝n＋4。‎ 过点D作DM⊥BC于M，则四边形ABND是矩形。‎ ‎∴BM＝AD＝1，DM＝AB＝2。∴CM＝BC－BM＝3－1＝2＝DM。‎ ‎∴∠DCM＝45°。∴∠KCH＝45°。‎ ‎∴CK＝CH•cos45°＝ (n＋4)，‎ ‎∴当PQ⊥CD时，PQ的长最小，最小值为 (n＋4)。‎ ‎【考点】反证法，相似三角形的判定和性质，一元二次方程根的判别式，全等三角形的判定和性质，勾股定理，平行四边形、矩形的判定和性质，等腰直角三角形的判定和性质。‎ ‎【分析】问题1：四边形PCQD是平行四边形，若对角线PQ、DC相等，则四边形PCQD是矩形，然后利用矩形的性质，设PB＝x，可得方程x2＋32＋(2－x)2＋1＝8，由判别式△＜0，可知此方程无实数根，即对角线PQ，DC的长不可能相等。‎ ‎ 问题2：在平行四边形PCQD中，设对角线PQ与DC相交于点G，可得G是DC的中点，过点Q作QH⊥BC，交BC的延长线于H，易证得Rt△ADP≌Rt△HCQ，即可求得BH＝4，则可得当PQ⊥AB时，PQ的长最小，即为4。‎ 问题3：设PQ与DC相交于点G，PE∥CQ，PD＝DE，可得，易证得Rt△ADP∽Rt△HCQ，继而求得BH的长，即可求得答案。‎ 问题4：作QH∥PE，交CB的延长线于H，过点C作CK⊥CD，交QH的延长线于K，易证得与△ADP∽△BHQ，又由∠DCB＝45°，可得△CKH是等腰直角三角形，继而可求得CK的值，即可求得答案。‎ ‎7. （（2012江苏南京9分）“？”的思考 下框中是小明对一道题目的解答以及老师的批阅。‎ 题目：某村计划建造如图所示的矩形蔬菜温室，要求长与宽的比为2：1，在温室内，沿前侧内墙保留‎3m的空地，其他三侧内墙各保留‎1m的通道，当温室的长与宽各为多少时，矩形蔬菜种植区域的面积是‎288m2‎？‎ 解：设矩形蔬菜种植区域的宽为xm，则长为2xm，‎ 根据题意，得x•2x=288．‎ 解这个方程，得x1=-12（不合题意，舍去），x2=12‎ 所以温室的长为2×12+3+1=28（m），宽为12+1+1=14（m）‎ 答：当温室的长为‎28m，宽为‎14m时，矩形蔬菜种植区域的面积是‎288m2‎．‎ ‎？‎ 我的结果也正确 小明发现他解答的结果是正确的，但是老师却在他的解答中划了一条横线，并打开了一个“？”‎ 结果为何正确呢？‎ ‎（1）请指出小明解答中存在的问题，并补充缺少的过程：‎ 变化一下会怎样…… ‎ ‎（2）如图，矩形A′B′C′D′在矩形ABCD的内部，AB∥A′B′，AD∥A′D′，且AD：AB=2：1，设AB与A′B′、BC与B′C′、CD与C′D′、DA与D′A′之间的距离分别为a、b、c、d，要使矩形A′B′C′D′∽矩形ABCD，a、b、c、d应满足什么条件？请说明理由．‎ ‎【答案】解：（1）小明没有说明矩形蔬菜种植区域的长与宽之比为2：1的理由。‎ 在“设矩形蔬菜种植区域的宽为xm，则长为2xm．”前补充以下过程：‎ 设温室的宽为ym，则长为2ym。‎ 则矩形蔬菜种植区域的宽为（y－1－1）m，长为（2y－3－1）m。‎ ‎∵，∴矩形蔬菜种植区域的长与宽之比为2：1。‎ ‎（2）a+c b+d =2。理由如下：‎ 要使矩形A′B′C′D′∽矩形ABCD，就要，即，‎ 即 ，即a+c b+d =2。‎ ‎【考点】一元二次方程的应用（几何问题），相似多边形的性质，比例的性质。‎ ‎【分析】（1）根据题意可得小明没有说明矩形蔬菜种植区域的长与宽之比为2：1的理由，所以由已知条件求出矩形蔬菜种植区域的长与宽的关系即可。‎ ‎（2）由使矩形A′B′C′D′∽矩形ABCD，利用相似多边形的性质，可得 ，然后利用比例的性质。‎ ‎8. （2012江苏南京10分）如图，A、B为⊙O上的两个定点，P是⊙O上的动点（P不与A、B重合），我们称∠APB为⊙O上关于A、B的滑动角。‎ ‎（1）已知∠APB是上关于点A、B的滑动角。‎ ‎① 若AB为⊙O的直径，则∠APB= ‎ ‎② 若⊙O半径为1，AB=，求∠APB的度数 ‎（2）已知为外一点，以为圆心作一个圆与相交于A、B两点，∠APB为上关于点A、B的滑动角，直线PA、PB分别交于点M、N（点M与点A、点N与点B均不重合），连接AN，试探索∠APB与∠MAN、∠ANB之间的数量关系。‎ ‎【答案】解：（1）①900。‎ ‎②如图，连接AB、OA、OB．‎ 在△AOB中，∵OA=OB=1．AB=，∴OA2+OB2=AB2。‎ ‎∴∠AOB=90°。‎ 当点P在优弧 AB 上时（如图1），∠APB=∠AOB=45°；‎ 当点P在劣弧 AB 上时（如图2），‎ ‎∠APB=（360°－∠AOB）=135°。‎ ‎（2）根据点P在⊙O1上的位置分为以下四种情况．‎ 第一种情况：点P在⊙O2外，且点A在点P与点M之间，点B在点P与点N之间，如图3，‎ ‎∵∠MAN=∠APB+∠ANB，‎ ‎∴∠APB=∠MAN-∠ANB。‎ 第二种情况：点P在⊙O2外，且点A在点P与点M之间，点N在点P与点B之间，如图4，‎ ‎∵∠MAN=∠APB+∠ANP=∠APB+（180°－∠ANB），‎ ‎∴∠APB=∠MAN+∠ANB－180°。‎ 第三种情况：点P在⊙O2外，且点M在点P与点A之间，点B在点P与点N之间，如图5，‎ ‎∵∠APB+∠ANB+∠MAN=180°，‎ ‎∴∠APB=180°－∠MAN－∠ANB。‎ 第四种情况：点P在⊙O2内，如图6，‎ ‎∠APB=∠MAN+∠ANB。‎ ‎【考点】圆周角定理，勾股定理逆定理，三角形内角和定理和外角性质。‎ ‎【分析】（1）①根据直径所对的圆周角等于90°即可得∠APB=900。‎ ‎②根据勾股定理的逆定理可得∠AOB=90°，再分点P在优弧上；点P在劣弧上两种情况讨论即可。‎ ‎（2）根据点P在⊙O1上的位置分为四种情况得到∠APB与∠MAN、∠ANB之间的数量关系。‎ ‎9. （2012江苏南通12分）如图，在△ABC中，AB＝AC＝‎10cm，BC＝‎12cm，点D是BC边的中点．点P从点B出发，以acm/s(a＞0)的速度沿BA匀速向点A运动；点Q同时以‎1cm/s的速度从点D出发，沿DB匀速向点B运动，其中一个动点到达端点时，另一个动点也随之停止运动，设它们运动的时间为ts．‎ ‎(1)若a＝2，△BPQ∽△BDA，求t的值；‎ ‎(2)设点M在AC上，四边形PQCM为平行四边形．‎ ‎①若a＝，求PQ的长；‎ ‎②是否存在实数a，使得点P在∠ACB的平分线上？若存在，请求出a的值；若不存在，请说明 理由．‎ ‎【答案】解：（1）△ABC中，AB=AC=10，BC=12，D是BC的中点，∴BD=CD=BC=6。‎ ‎∵a=2，∴BP=2t，DQ=t。∴BQ=BD－QD=6－t。‎ ‎∵△BPQ∽△BDA，∴，即，解得：。‎ ‎（2）①过点P作PE⊥BC于E，‎ ‎∵四边形PQCM为平行四边形，‎ ‎∴PM∥CQ，PQ∥CM，PQ=CM。‎ ‎∴PB：AB=CM：AC。‎ ‎∵AB=AC，∴PB=CM。∴PB=PQ。‎ ‎∴BE=BQ=（6－t）。‎ ‎∵a=，∴PB=t。‎ ‎∵AD⊥BC，∴PE∥AD。∴PB：AB=BE：BD，即。‎ 解得，t=。‎ ‎∴PQ=PB=t=（cm）。‎ ‎②不存在．理由如下：‎ ‎∵四边形PQCM为平行四边形，∴PM∥CQ，PQ∥CM，PQ=CM。‎ ‎∴PB：AB=CM：AC。‎ ‎∵AB=AC，∴PB=CM，∴PB=PQ。‎ 若点P在∠ACB的平分线上，则∠PCQ=∠PCM，‎ ‎∵PM∥CQ，∴∠PCQ=∠CPM。∴∠CPM=∠PCM。‎ ‎∴PM=CM。∴四边形PQCM是菱形。∴PQ=CQ。‎ ‎∴PB=CQ。‎ ‎∵PB=at，CQ=BD+QD=6+t，∴PM=CQ=6+t，AP=AB－PB=10－at，且 at=6+t①。‎ ‎∵PM∥CQ，∴PM：BC=AP：AB，∴，化简得：6at+5t=30②。‎ 把①代入②得，t=。‎ ‎∴不存在实数a，使得点P在∠ACB的平分线上。‎ ‎【考点】等腰三角形的性质，相似三角形的判定和性质，平行四边形的性质，平行的性质，菱形的判定和性质，反证法。‎ ‎【分析】（1）由△ABC中，AB=AC=10，BC=12，D是BC的中点，根据等腰三角形三线合一的性质，‎ 即可求得BD与CD的长，又由a=2，△BPQ∽△BDA，利用相似三角形的对应边成比例，即可求得t的值。‎ ‎（2）①首先过点P作PE⊥BC于E，由四边形PQCM为平行四边形，易证得PB=PQ，又由平行 线分线段成比例定理，即可得方程，解此方程即可求得答案。‎ ‎②用反证法，假设存在点P在∠ACB的平分线上，由四边形PQCM为平行四边形，可得四边形PQCM是菱形，即可得PB=CQ，PM：BC=AP：PB，及可得方程组，解此方程组求得t值为负，故可得不存在。‎ ‎10. （2012江苏南通14分）如图，经过点A(0，－4)的抛物线y＝x2＋bx＋c与x轴相交于点B(－0，0)和C，O为坐标原点．‎ ‎(1)求抛物线的解析式；‎ ‎(2)将抛物线y＝x2＋bx＋c向上平移个单位长度、再向左平移m(m＞0)个单位长度，得到新抛物 线．若新抛物线的顶点P在△ABC内，求m的取值范围；‎ ‎(3)设点M在y轴上，∠OMB＋∠OAB＝∠ACB，求AM的长． ‎ ‎【答案】解：（1）将A（0，－4）、B（－2，0）代入抛物线y=x2+bx+c中，得：‎ ‎ ，解得，。 ‎ ‎∴抛物线的解析式：y=x2－x－4。源:学科网ZXXK]‎ ‎（2）由题意，新抛物线的解析式可表示为：，‎ 即：。它的顶点坐标P（1－m，－1）。‎ 由（1）的抛物线解析式可得：C（4，0）。‎ ‎∴直线AB：y=－2x-4；直线AC：y=x－4。‎ 当点P在直线AB上时，－2（1－m）－4=－1，解得：m=；‎ 当点P在直线AC上时，（1－m）＋4=－1，解得：m=－2；‎ 又∵m＞0，‎ ‎∴当点P在△ABC内时，0＜m＜ 。‎ ‎（3）由A（0，-4）、B（4，0）得：OA=OC=4，且△OAC是等腰直角三角形。‎ 如图，在OA上取ON=OB=2，则∠ONB=∠ACB=45°。‎ ‎∴∠ONB=∠NBA+OAB=∠ACB=∠OMB+∠OAB，‎ 即∠ONB=∠OMB。‎ 如图，在△ABN、△AM1B中，‎ ‎∠BAN=∠M1AB，∠ABN=∠AM1B，‎ ‎∴△ABN∽△AM1B，得：AB2=AN•AM1；‎ 由勾股定理，得AB2=（－2）2+42=20，‎ 又AN=OA－ON=4－2=2，‎ ‎∴AM1=20÷2=10，OM1=AM1－OA=10－4=6。‎ 而∠BM‎1A=∠BM‎2A=∠ABN，∴OM1=OM2=6，AM2=OM2－OA=6－4=2。‎ 综上，AM的长为6或2。‎ ‎【考点】二次函数综合题，曲线上点的坐标与方程的关系，平移的性质，二次函数的性质，等腰直角三角形的判定和性质，勾股定理。‎ ‎【分析】（1）该抛物线的解析式中只有两个待定系数，只需将A、B两点坐标代入即可得解。‎ ‎（2）首先根据平移条件表示出移动后的函数解析式，从而用m表示出该函数的顶点坐标，将其 代入直线AB、AC的解析式中，即可确定P在△ABC内时m的取值范围。‎ ‎（3）先在OA上取点N，使得∠ONB=∠ACB，那么只需令∠NBA=∠OMB即可，显然在y轴的正负半轴上都有一个符合条件的M点；以y轴正半轴上的点M为例，先证△ABN、△AMB相似，然后通过相关比例线段求出AM的长。‎ ‎11. （2012江苏苏州9分）如图，正方形ABCD的边AD与矩形EFGH的边FG重合，将正方形ABCD 以‎1cm/s的速度沿FG方向移动，移动开始前点A与点F重合.在移动过程中，边AD始终与边FG重合，‎ 连接CG，过点A作CG的平行线交线段GH于点P，连接PD.已知正方形ABCD的边长为‎1cm，矩形EFGH 的边FG、GH的长分别为‎4cm、‎3cm.设正方形移动时间为x（s），线段GP的长为y（cm），其中 ‎0≤x≤2.5.‎ ‎ ⑴试求出y关于x的函数关系式，并求出y =3时相应x的值；‎ ‎⑵记△DGP的面积为S1，△CDG的面积为S2．试说明S1－S2是常数；‎ ‎⑶当线段PD所在直线与正方形ABCD的对角线AC垂直时，求线段PD的长.‎ ‎【答案】解：（1）∵CG∥AP，∴∠CGD=∠PAG，则。∴。‎ ‎∵GF=4，CD=DA=1，AF=x，∴GD=3－x，AG=4－x。‎ ‎∴，即。∴y关于x的函数关系式为。‎ 当y =3时，，解得:x=2.5。‎ ‎（2）∵， ‎∴为常数。‎ ‎（3）延长PD交AC于点Q.‎ ‎∵正方形ABCD中，AC为对角线，∴∠CAD=45°。‎ ‎∵PQ⊥AC，∴∠ADQ=45°。‎ ‎∴∠GDP=∠ADQ=45°。‎ ‎∴△DGP是等腰直角三角形，则GD=GP。‎ ‎∴，化简得：，解得：。 ‎∵0≤x≤2.5，∴。‎ 在Rt△DGP中，。‎ ‎【考点】正方形的性质，一元二次方程的应用，等腰直角三角形的性质，矩形的性质，解直角三角形，锐角三角函数定义，特殊角的三角函数值。‎ ‎【分析】（1）根据题意表示出AG、GD的长度，再由可解出x的值。‎ ‎（2）利用（1）得出的y与x的关系式表示出S1、S2，然后作差即可。‎ ‎（3）延长PD交AC于点Q，然后判断△DGP是等腰直角三角形，从而结合x的范围得出x的值，在Rt△DGP中，解直角三角形可得出PD的长度。‎ ‎12. （2012江苏苏州10分）如图，已知抛物线（b是实数且b＞2）与x轴的正半轴 分别交于点A、B（点A位于点B的左侧），与y轴的正半轴交于点C.‎ ‎ ⑴点B的坐标为 ▲ ，点C的坐标为 ▲ （用含b的代数式表示）；‎ ‎⑵请你探索在第一象限内是否存在点P，使得四边形PCOB的面积等于2b，且△PBC是以点P为直角 顶点的等腰直角三角形？如果存在，求出点P的坐标；如果不存在，请说明理由；‎ ‎⑶请你进一步探索在第一象限内是否存在点Q，使得△QCO、△QOA和△QAB中的任意两个三角形 均相似（全等可看作相似的特殊情况）？如果存在，求出点Q的坐标；如果不存在，请说明理由.‎ ‎【答案】解：（1）B（b，0），C（0，）。‎ ‎（2）假设存在这样的点P，使得四边形PCOB的面积等于2b，且△PBC是以点P为直角顶 点的等腰直角三角形。‎ ‎ 设点P坐标（x，y），连接OP，‎ ‎ 则 ‎∴。‎ 过P作PD⊥x轴，PE⊥y轴，垂足分别为D、E，‎ ‎∴∠PEO=∠EOD=∠ODP=90°。∴四边形PEOD是矩形。‎ ‎∴∠EPD=90°。‎ ‎∵△PBC是等腰直角三角形，∴PC=PB，∠BPC=90°。‎ ‎∴∠EPC=∠BPD。∴△PEC≌△PDB（AAS）。∴PE=PD，即x=y。‎ 由 解得，。‎ 由△PEC≌△PDB得EC=DB，即，解得符合题意。‎ ‎∴点P坐标为（，）。‎ ‎（3）假设存在这样的点Q，使得△QCO、△QOA和△QAB中的任意两个三角形均相似.‎ ‎ ∵∠QAB=∠AOQ+∠AQO，∴∠QAB＞∠AOQ，∠QAB＞∠AQO.‎ ‎∴要使得△QOA和△QAB相似，只能∠OAQ=∠QAB=90°，即QA⊥x轴。‎ ‎∵b＞2，∴AB＞OA. ∴∠QOA＞∠QBA，∴∠QOA=∠AQB，此时∠OQB =90°。‎ 由QA⊥x轴知QA∥y轴，∴∠COQ=∠OQA。‎ ‎∴要使得△QOA和△OQC相似，只能∠OCQ=90°或∠OQC=90°。‎ ‎（Ⅰ）当∠OCQ=90°时，△QOA≌△OQC，∴AQ=CO=。‎ ‎ 由 得：，解得：。‎ ‎∵b＞2，∴。∴点Q坐标为（1，）.‎ ‎（Ⅱ）当∠OQC=90°时，△QOA∽△OCQ，∴，即。‎ 又，∴，即，解得：AQ=4‎ 此时b=17＞2符合题意。∴点Q坐标为（1，4）。‎ 综上可知：存在点Q（1，）或（1，4），使得△QCO、△QOA和△QAB中的任 意两个三角形均相似。‎ ‎【考点】二次函数综合题，曲线上点的坐标与方程的关系，等腰直角三角形的判定和性质，矩形的判定和性质，全等三角形的判定和性质，相似三角形的判定和性质。‎ ‎【分析】（1）令y=0，即，解关于x的一元二次方程即可求出A，B横坐标，令 x=0，求出y的值即C的纵坐标。‎ ‎（2）存在，先假设存在这样的点P，使得四边形PCOB的面积等于2b，且△PBC是以点P为直 角顶点的等腰直角三角形．设点P的坐标为（x，y），连接OP，过P作PD⊥x轴，PE⊥y轴，垂足分别为D、E，利用已知条件证明△PEC≌△PDB，进而求出x和y的值，从而求出P的坐标。‎ ‎（3）存在，假设存在这样的点Q，使得△QCO，△QOA和△QAB中的任意两个三角形均相似，‎ 由条件可知：要使△QOA与△QAB相似，只能∠QAO=∠BAQ=90°，即QA⊥x轴；要使△QOA与△OQC相似，只能∠QCO=90°或∠OQC=90°。再分别讨论求出满足题意Q的坐标即可。‎ ‎13. （2012江苏宿迁12分）(1)如图1，在△ABC中，BA=BC，D，E是AC边上的两点，且满足∠DBE=∠ABC(0°＜∠CBE＜∠ABC)。以点B为旋转中心，将△BEC按逆时针方向旋转∠ABC，得到△BE’A（点C与点A重合，点E到点E’处），连接DE’。求证：DE’=DE. ‎ ‎（2）如图2，在△ABC中，BA=BC，∠ABC=90°，D，E是AC边上的两点，‎ 且满足∠DBE=∠ABC(0°＜∠CBE＜45°).求证：DE2=AD2+EC2.[来 ‎:学#科#网]‎ ‎【答案】证明：（1）∵△BE’A是△BEC按逆时针方向旋转∠ABC得到，‎ ‎ ∴BE’=BE，∠E’BA=∠EBC。‎ ‎ ∵∠DBE=∠ABC，∴∠ABD＋∠EBC =∠ABC。‎ ‎ ∴∠ABD＋∠E’BA =∠ABC，即∠E’BD=∠ABC。∴∠E’BD=∠DBE。‎ ‎ 在△E’BD和△EBD中，∵BE’=BE，∠E’BD=∠DBE，BD=BD，‎ ‎ ∴△E’BD≌△EBD（SAS）。∴DE’=DE。‎ ‎（2）以点B为旋转中心，将△BEC按逆时针方向旋转∠ABC=90°，得到△BE’A（点C与点A重合，点E到点E’处），连接DE’。‎ ‎ 由（1）知DE’=DE。‎ ‎ 由旋转的性质，知E’A=EC，∠E’ AB=∠ECB。‎ ‎ 又∵BA=BC，∠ABC=90°，∴∠BAC=∠ACB=45°。‎ ‎ ∴∠E’ AD=∠E’ AB＋∠BAC=90°。‎ ‎ 在Rt△DE’A中，DE’2=AD2+E’A2，∴DE2=AD2+EC2。‎ ‎【考点】旋转的性质，等腰（直角）三角形的性质，全等三角形的判定和性质，勾股定理。‎ ‎【分析】（1）由旋转的性质易得BE’=BE，∠E’BA=∠EBC，由已知∠DBE=∠ABC经等量代换可得 ‎∠E’BD=∠DBE，从而可由SAS得△E’BD≌△EBD，得到DE’=DE。‎ ‎（2）由（1）的启示，作如（1）的辅助图形，即可得到直角三角形DE’A ‎，根据勾股定理即可证得结论。‎ ‎14. （2012江苏宿迁12分）如图，在平面直角坐标系xoy中，已知直线l1:y=x与直线l2：y=－x+6相交于点M，直线l2与x轴相较于点N.‎ （1） 求M，N的坐标；‎ （2） 在矩形ABCD中，已知AB=1，BC=2，边AB在x轴上，矩形ABCD沿x轴自左向右以每秒1个 单位长度的速度移动.设矩形ABCD与△OMN的重叠部分的面积为S.移动的时间为t（从点B与点O重合时开始计时，到点A与点N重合时计时结束）。直接写出S与自变量t之间的函数关系式（不需要给出解答过程）；‎ （3） 在（2）的条件下，当t为何值时，S的值最大？并求出最大值.‎ ‎【答案】解：（1）解得。∴M的坐标为（4，2）。‎ ‎ 在y=－x+6中令y=0得x=6，∴N的坐标为（6，0）。‎ ‎ （2）S与自变量t之间的函数关系式为：‎ ‎ ‎ ‎ （3）当0≤t≤1时，S的最大值为，此时t=1。‎ ‎ 当1＜t≤4时，S的最大值为，此时t=4。‎ ‎ 当4＜t≤5时，∵，‎ ‎∴S的最大值为，此时t=。‎ ‎ 当5＜t≤6时，S随t的增大而减小，最大值不超过。‎ ‎ 当6＜t≤7时，S随t的增大而减小，最大值不超过。‎ ‎ 综上所述，当t=时，S的值最大，最大值为。‎ ‎【考点】一次函数综合题，平移问题，直线上点的坐标与方程的关系，一次函数和二次函数的最值。‎ ‎【分析】（1）联立两直线方程即可求得M的坐标，在y=－x+6中令y=0即可求得N的坐标。‎ ‎（2）先求各关键位置，自变量t的情况：‎ 起始位置时，t=0；当点A与点O重合时，如图1，t=1；当点C与点M重合时，如图2，t=4；当点D与点M重合时，如图3，t=5；当点B与点N重合时，如图4，t=6；结束位置时，点A与点N重合，t=7。‎ ①当0≤t≤1时，矩形ABCD与△OMN的重叠部分的面积为一三角形面积（不含t=0），三角形的底为t，高为，∴。‎ ②当1＜t≤4时，矩形ABCD与△OMN的重叠部分的面积为一梯形面积，梯形的上底为，下底为，高为1。∴。‎ ③当4＜t≤5时，矩形ABCD与△OMN的重叠部分的面积为两梯形面积的和，第一个梯形的上底为，下底为2，高为；第二个梯形的上底为－t ‎ ‎+6，下底为2，高为。‎ ‎∴。‎ ④当5＜t≤6时，矩形ABCD与△OMN的重叠部分的面积为一梯形面积，梯形的上底为 ‎6－t ，下底为7－t，高为1。∴。‎ ⑤当6＜t≤7时，矩形ABCD与△OMN的重叠部分的面积为一三角形面积（不含t=7），三角形的底为7－t，高为7－t，∴。‎ ‎（3）分别讨论各分段函数的最大值而得所求。‎ ‎15. （2012江苏泰州12分）如图，已知直线l与⊙O相离，OA⊥l于点A，OA=5，OA与⊙O相交于点 P，AB与⊙O相切于点B，BP的延长线交直线l于点C．‎ ‎（1）试判断线段AB与AC的数量关系，并说明理由；‎ ‎（2）若PC=，求⊙O的半径和线段PB的长；‎ ‎（3）若在⊙O上存在点Q，使△QAC是以AC为底边的等腰三角形，求⊙O的半径r的取值范围．‎ ‎【答案】解：（1）AB=AC。理由如下：‎ 连接OB。‎ ‎∵AB切⊙O于B，OA⊥AC，∴∠OBA=∠OAC=90°。‎ ‎∴∠OBP+∠ABP=90°，∠ACP+∠CPB=90°。‎ ‎∵OP=OB，∴∠OBP=∠OPB。‎ ‎∵∠OPB=∠APC，∴∠ACP=∠ABC。‎ ‎∴AB=AC。‎ ‎（2）延长AP交⊙O于D，连接BD，‎ 设圆半径为r，则由OA=5得，OP=OB=r，PA=5－r。‎ 又∵PC=，‎ ‎∴ 。‎ 由（1）AB=AC得，解得：r=3。‎ ‎∴AB=AC=4。‎ ‎∵PD是直径，∴∠PBD=90°=∠PAC。‎ ‎∵∠DPB=∠CPA，∴△DPB∽△CPA。∴，即，解得。‎ ‎ （3）作线段AC的垂直平分线MN，作OE⊥MN，‎ 则OE=AC=AB=。‎ 又∵圆O要与直线MN交点，∴OE=≤r，‎ ‎∴r≥。‎ 又∵圆O与直线l相离，∴r＜5。‎ ‎∴⊙O的半径r的取值范围为≤r＜5．‎ ‎【考点】切线的性质，三角形内角和定理，等腰三角形的判定和性质，勾股定理，直线与圆的位置关系，相似三角形的判定和性质。‎ ‎【分析】（1）连接OB，根据切线的性质和垂直得出∠OBA=∠OAC=90°，推出∠OBP+∠ABP=90°，‎ ‎∠ACP+∠CPB=90°，求出∠ACP=∠ABC，根据等腰三角形的判定推出即可。‎ ‎（2）延长AP交⊙O于D，连接BD，设圆半径为r，则OP=OB=r，PA=5－r，根据AB=AC推出 ‎，求出r，证△DPB∽△CPA，得出 ，代入求出PB即可。‎ ‎（3）根据已知得出Q在AC的垂直平分线上，作出线段AC的垂直平分线MN，作OE⊥MN，求出OE＜r，求出r范围，再根据相离得出r＜5，即可得出答案。‎ ‎16. （2012江苏泰州12分） 如图，已知一次函数的图象与x轴相交于点A，与反比例函数 的图象相交于B（－1，5）、C（，d）两点．点P（m，n）是一次函数的图象上的动点．‎ ‎（1）求k、b的值；‎ ‎（2）设，过点P作x轴的平行线与函数的图象相交于点D．试问△PAD的面积是 否存在最大值？若存在，请求出面积的最大值及此时点P的坐标；若不存在，请说明理由；‎ ‎（3）设，如果在两个实数m与n之间（不包括m和n）有且只有一个整数，求实数a的取值 范围．‎ ‎【答案】解：（1）将点B 的坐标代入，得 ，解得。‎ ‎ ∴反比例函数解析式为。‎ ‎ 将点C（，d）的坐标代入，得。∴C（，－2）。‎ ‎ ∵一次函数的图象经过B（－1，5）、C（，－2）两点，‎ ‎ ∴，解得。‎ ‎（2）存在。‎ ‎ 令，即，解得。∴A（，0）。‎ ‎ 由题意，点P（m，n）是一次函数的图象上的动点，且 ‎ ∴点P在线段AB 上运动（不含A、B）。设P（）。‎ ‎ ∵DP∥x轴，且点D在的图象上，‎ ‎ ∴，即D（）。‎ ‎ ∴△PAD的面积为。‎ ‎ ∴S关于n的二次函数的图象开口向下，有最大值。‎ ‎ 又∵n=，，得，而。‎ ‎ ∴当时，即P（）时，△PAD的面积S最大，为。‎ ‎ （3）由已知，P（）。‎ ‎ 易知m≠n，即，即。‎ ‎ 若，则。‎ ‎ 由题设，，解出不等式组的解为。‎ ‎ 若，则。‎ ‎ 由题设，，解出不等式组的解为。‎ ‎ 综上所述，数a的取值范围为，。‎ ‎【考点】反比例函数和一次函数综合问题，曲线上点的坐标与方程的关系，平行的性质，二次函数的性质，不等式组的应用。‎ ‎【分析】（1）根据曲线上点的坐标与方程的关系，由B 的坐标求得，从而得到；由点C在上求得，即得点C的坐标；由点B、C在上，得方程组，解出即可求得k、b的值。 ‎ ‎ （2）求出△PAD的面积S关于n的二次函数（也可求出关于m），应用二次函数的最值原理即可求得面积的最大值及此时点P的坐标。‎ ‎（3）由m≠n得到。分和两种情况求解。‎ ‎17. （2012江苏无锡8分）对于平面直角坐标系中的任意两点P1（x1，y1），P2（x2，y2），我们把|x1﹣x2|+|y1﹣y2|叫做P1、P2两点间的直角距离，记作d（P1，P2）．‎ ‎（1）已知O为坐标原点，动点P（x，y）满足d（O，P）=1，请写出x与y之间满足的关系式，并在所给的直角坐标系中画出所有符合条件的点P所组成的图形；‎ ‎（2）设P0（x0，y0）是一定点，Q（x，y）是直线y=ax+b上的动点，我们把d（P0，Q）的最小值叫做P0到直线y=ax+b的直角距离．试求点M（2，1）到直线y=x+2的直角距离．‎ ‎【答案】解：（1）由题意，得|x|+|y|=1。‎ 所有符合条件的点P组成的图形如图所示：‎ ‎（2）∵d（M，Q）=|x﹣2|+|y﹣1|=|x﹣2|+|x+2﹣1|=|x﹣2|+|x+1|，‎ 又∵x可取一切实数，|x﹣2|+|x+1|表示数轴上实数x所对应的点到数2和﹣1所对应的点的距离之和，其最小值为3。‎ ‎∴点M（2，1）到直线y=x+2的直角距离为3。‎ ‎【考点】新定义，一次函数综合题，绝对值与数轴的关系。‎ ‎【分析】（1）根据新定义知|x|+|y|=1，据此可以画出符合题意的图形。‎ ‎（2）根据新定义知d（M，Q）=|x﹣2|+|y﹣1|=|x﹣2|+|x+2﹣1|=|x﹣2|+|x+1|，然后由绝对值与数轴的关系可知，|x﹣2|+|x+1|表示数轴上实数x所对应的点到数2和﹣1所对应的点的距离之和，其最小值为3。‎ ‎18. （2012江苏无锡10分）如图，菱形ABCD的边长为‎2cm，∠DAB=60°．点P从A点出发，以cm/s的速度，沿AC向C作匀速运动；与此同时，点Q也从A点出发，以‎1cm/s 的速度，沿射线AB作匀速运动．当P运动到C点时，P、Q都停止运动．设点P运动的时间为ts．‎ ‎（1）当P异于A．C时，请说明PQ∥BC；‎ ‎（2）以P为圆心、PQ长为半径作圆，请问：在整个运动过程中，t为怎样的值时，⊙P与边BC分别有1个公共点和2个公共点？‎ ‎【答案】解：（1）∵四边形ABCD是菱形，且菱形ABCD的边长为2，‎ ‎∴AB=BC=2，∠BAC=∠DAB。‎ 又∵∠DAB=60°，∴∠BAC=∠BCA=30°。‎ 如图1，连接BD交AC于O。‎ ‎∵四边形ABCD是菱形，‎ ‎∴AC⊥BD，OA=AC。‎ ‎∴OB=AB=1。∴OA=，AC=2OA=2。‎ 运动ts后，AP=t，AO=t，∴。‎ 又∵∠PAQ=∠CAB，∴△PAQ∽△CAB.∴∠APQ=∠ACB.‎ ‎∴PQ∥BC.‎ ‎（2）如图2，⊙P与BC切于点M，连接PM，则PM⊥BC。‎ 在Rt△CPM中，∵∠PCM=30°，∴PM=。‎ 由PM=PQ=AQ=t，即=t，解得t=，‎ 此时⊙P与边BC有一个公共点。‎ 如图3，⊙P过点B，此时PQ=PB，‎ ‎∵∠PQB=∠PAQ+∠APQ=60°‎ ‎∴△PQB为等边三角形。∴QB=PQ=AQ=t。∴t=1。‎ ‎∴当时，⊙P与边BC有2个公共点。‎ 如图4，⊙P过点C，此时PC=PQ，即 =t ‎∴t=。‎ ‎∴当1≤t≤时，⊙P与边BC有一个公共点。‎ 当点P运动到点C，即t=2时，Q、B重合，⊙P过点B，‎ 此时，⊙P与边BC有一个公共点。‎ 综上所述，当t=或1≤t≤或t=2时，⊙P与菱形ABCD的边BC有1个公共点；当时，⊙P与边BC有2个公共点。‎ ‎【考点】直线与圆的位置关系，菱形的性质，含30°角直角三角形的性质，相似三角形的判定和性质，平行的判定，切线的性质，等边三角形的判定和性质。‎ ‎【分析】（1）连接BD交AC于O，构建直角三角形AOB．利用菱形的对角线互相垂直、对角线平分对角、邻边相等的性质推知△PAQ∽△CAB；然后根据“相似三角形的对应角相等”证得∠APQ=∠ACB；最后根据平行线的判定定理“同位角相等，两直线平行”可以证得结论。‎ ‎（2）分⊙P与BC切于点M，⊙P过点B，⊙P过点C和点P运动到点C四各情况讨论即可。‎ ‎19. （2012江苏徐州8分）如图1，A、B、C、D为矩形的四个顶点，AD=‎4cm，AB=dcm。动点E、F分别从点D、B出发，点E以‎1 cm/s的速度沿边DA向点A移动，点F以‎1 cm/s的速度沿边BC向点C移动，点F移动到点C时，两点同时停止移动。以EF为边作正方形EFGH，点F出发xs时，正方形EFGH的面积为ycm2。已知y与x的函数图象是抛物线的一部分，如图2所示。请根据图中信息，解答下列问题：‎ ‎（1）自变量x的取值范围是 ▲ ；‎ ‎（2）d= ▲ ，m= ▲ ，n= ▲ ；‎ ‎（3）F出发多少秒时，正方形EFGH的面积为‎16cm2？‎ ‎【答案】解：（1）0≤x≤4。‎ ‎ （2）3，2，25．‎ ‎ （3）过点E作EI⊥BC垂足为点I。则四边形DEIC为矩形。‎ ‎ ∴EI=DC=3，CI=DE=x。‎ ‎ ∵BF=x，∴IF=4－2x。‎ ‎ 在Rt△EFI中，。‎ ‎ ∵y是以EF为边长的正方形EFGH的面积，‎ ‎ ∴。‎ ‎ 当y=16时，，‎ 解得，。‎ ‎∴F出发或秒时，正方形EFGH的面积为‎16cm2。‎ ‎【考点】动点问题，矩形的判定和性质，平行线间垂直线段的性质，勾股定理，解一元二次方程。‎ ‎【分析】（1）自变量x的取值范围是点F从点C到点B的运动时间，由时间=距离÷速度，即可求。‎ ‎ （2）由图2知，正方形EFGH的面积的最小值是9，而正方形EFGH的面积最小时，根据地两平行线间垂直线段最短的性质，得d=AB=EF=3。‎ ‎ 当正方形EFGH的面积最小时，由BF=DE和EF∥AB得，E、F分别为AD、BC的中点，即m=2。‎ ‎ 当正方形EFGH的面积最大时，EF等于矩形ABCD的对角线，根据勾股定理，它为5，即n=25。‎ ‎ （3）求出正方形EFGH的面积y关于x的函数关系式，即可求得F出发或秒时，正方形EFGH的面积为‎16cm2。‎ ‎20. （2012江苏徐州10分）如图，直线与x轴、y轴分别相交于点A、B，与正比例函数的图象相交于点C、D（点C在点D的左侧），⊙O是以CD长为半径的圆。CE∥x轴，DE∥y轴，CE、DE相交于点E。‎ ‎（1）△CDE是 ▲ 三角形；点C的坐标为 ▲ ，点D的坐标为 ▲ （用含有b的代数式表示）；‎ ‎（2）b为何值时，点E在⊙O上？‎ ‎（3）随着b取值逐渐增大，直线与⊙O有哪些位置关系？求出相应b的取值范围。‎ ‎【答案】解：（1）等腰直角；；。‎ ‎ （2）当点E在⊙O上时，如图，连接OE。则OE=CD。‎ ‎ ∵直线与x轴、y轴相交于点A（－b，0），B（0，b），CE∥x轴，DE∥y轴，‎ ‎ ∴△DCE、△BDO是等腰直角三角形。‎ ‎ ∵整个图形是轴对称图形，‎ ‎ ∴OE平分∠AOB，∠AOE=∠BOE=450。‎ ‎ ∵CE∥x轴，DE∥y轴，‎ ‎ ∴四边形CAOE、OEDB是等腰梯形。‎ ‎ ∴OE=AC=BD。‎ ‎ ∵OE=CD，∴OE=AC=BD=CD。‎ ‎ 过点C作CF⊥x轴，垂足为点F。‎ ‎ 则△AFC∽△AOB。∴。∴。‎ ‎ ∴，解得。‎ ‎ ∵，∴。‎ ‎ ∴当时，点E在⊙O上。‎ ‎（3）当⊙O与直线相切于点G时，‎ ‎ 如图 ，连接OG。‎ ‎ ∵整个图形是轴对称图形，‎ ‎ ∴点O、E、G在对称轴上。‎ ‎∴GC=GD=CD=OG=AG。∴AC=CG=GD=DB。∴AC=AB。‎ 过点C作CH⊥x轴，垂足为点H。 则△AHC∽△AOB。‎ ‎∴。∴。‎ ‎∴，解得。‎ ‎∵，∴。‎ ‎∴当时，直线与⊙O相切；‎ 当时，直线与⊙O相离；‎ 当时，直线与⊙O相交。‎ ‎【考点】反比例函数和一次函数交点问题，等腰直角三角形的判定和性质，曲线上点的坐标与方程的关系，轴对称图形的性质，等腰梯形的判定和性质，相似三角形的判定和性质，直线和圆的位置关系。‎ ‎【分析】（1）∵直线与x轴、y轴相交于点A（－b，0），B（0，b），CE∥x轴，DE∥y轴，‎ ‎ ∴△DCE是等腰直角三角形。‎ ‎ 解得，或。‎ ‎ ∵点C在点D的左侧，∴点C的坐标为，点D的坐标为。‎ ‎（2）连接OE，过点C作CH⊥x轴于点H。由整个图形是轴对称图形，可求得OE=AC=BD=CD。由△AFC∽△AOB可求得，代入CF、BO关于b的关系式求解即得所求。‎ ‎（3）讨论直线与⊙O相切时，b的取值即可得到直线与⊙O的位置关系。‎ ‎ 当⊙O与直线相切于点G时，连接OG，过点C作CH⊥x轴于点H。由整个图形是轴对称图形，可求得AC=CG=GD=DB，即AC=AB。由△AHC∽△AOB可求得，代入CH、BO关于b的关系式求解即得⊙O与直线相切时相应b的值。从而得到直线与⊙O相离和相交时相应b的取值范围。‎ ‎21. （2012江苏盐城12分）‎ ‎ 知识迁移： 当且时，因为≥,所以≥,从而≥(当 时取等号).记函数,由上述结论可知：当时,该函数有最小值为.‎ ‎ 直接应用：已知函数与函数, 则当_________时,取得最小值 为_________.‎ ‎ 变形应用：已知函数与函数,求的最小值,并指出取得该 最小值时相应的的值.‎ ‎ 实际应用：已知某汽车的一次运输成本包含以下三个部分：一是固定费用,共元；二是燃油费,每 千米为元；三是折旧费,它与路程的平方成正比,比例系数为.设该汽车一次运输的路程为千米,‎ 求当为多少时,该汽车平均每千米的运输成本最低？最低是多少元？‎ ‎【答案】解：直接应用：1；2 。‎ 变形应用：∵ ，‎ ‎∴有最小值为。‎ 当，即时取得该最小值。‎ 实际应用：设该汽车平均每千米的运输成本为元，则 ‎， ‎ ‎∴当(千米)时, ‎ 该汽车平均每千米的运输成本最低，‎ 最低成本为元。‎ ‎【考点】二次函数的应用，几何不等式。‎ ‎【分析】直接运用：可以直接套用题意所给的结论，即可得出结果：‎ ‎∵函数,由上述结论可知：当时,‎ 该函数有最小值为，‎ ‎∴函数与函数，则当时，取得最小值为。‎ 变形运用：先得出的表达式，然后将看做一个整体，再运用所给结论即可。‎ 实际运用：设该汽车平均每千米的运输成本为元，则可表示出平均每千米的运输成本，利用所 给的结论即可得出答案。‎ ‎22. （2012江苏盐城12分）在平面直角坐标系中，已知二次函数的图象经过点和点，直线经过抛物线的顶点且与轴垂直，垂足为.‎ (1) 求该二次函数的表达式；‎ (2) 设抛物线上有一动点从点处出发沿抛物线向上运动,其纵坐标随时间 ‎≥)的变化规律为.现以线段为直径作.‎ ‎①当点在起始位置点处时，试判断直线与的位置关系，并说明理由；在点运动的过 程中，直线与是否始终保持这种位置关系? 请说明你的理由；‎ ‎②若在点开始运动的同时，直线也向上平行移动，且垂足的纵坐标随时间的变化规律为 ‎，则当在什么范围内变化时，直线与相交? 此时，若直线被所截得的弦长为,试求的最大值.‎ ‎【答案】解：（1）将点和点的坐标代入,得 ‎，解得。‎ ‎∴二次函数的表达式为。‎ ‎（2）①当点在点处时，直线与相切。理由如下：‎ ‎∵点，∴圆心的坐标为，的半径为。‎ 又抛物线的顶点坐标为（0，－1），即直线上所有点的巫坐标均为－1，从而圆心到直线的距离为。‎ ‎∴直线与相切。‎ ‎ 在点运动的过程中，直线与始终保持相切的位置关系。理由如下：‎ 设点，则圆心的坐标为，‎ ‎∴圆心到直线的距离为。‎ 又∵，∴。‎ 则的半径为。‎ ‎∴直线与始终相切。‎ ‎ ②由①知的半径为，‎ ‎ 又∵圆心的纵坐标为，直线上的点的纵坐标为，‎ ‎ ∴(ⅰ)当≥,即≤时，圆心到直线的距离为 ‎。‎ 则由，得，解得, ‎ ‎∴此时≤。‎ ‎(ⅱ)当＜,即＞时, 圆心到直线的距离为 ‎。‎ 则由,得，解得。‎ ‎∴此时＜。‎ 综上所述，当时,直线与相交。‎ ‎∵当时，圆心到直线的距离为，又半径为，∴。‎ ‎∴当时, 取得最大值为。‎ ‎【考点】二次函数综合题，曲线上点的坐标与方程的关系，直线与圆的位置关系，勾股定理，点到直线的距离，二次函数的性质。‎ ‎【分析】（1）所求函数的解析式中有两个待定系数，直接将点和点坐标代入即可得解。‎ ‎（2）①由于是的直径，由点的纵坐标可表示出点的纵坐标，从而能表示出到直线的距离，长易得。然后通过比较的半径和到直线的距离，即可判定直线与的位置关系。‎ ‎ ②该题要分两问来答，首先看第一问；该小题的思路和①完全一致，唯一不同的地方：要注意直线与的位置关系（需要考虑到到直线的表达方式）。‎ 在第二问中， 最大，那么求出关于的函数关系式，应用二次函数的最值原理即可求解。‎ ‎23. （2012江苏扬州12分）已知抛物线y＝ax2＋bx＋c经过A(－1，0)、B(3，0)、C(0，3)三点，直线l是抛物线的对称轴．‎ ‎(1)求抛物线的函数关系式；‎ ‎(2)设点P是直线l上的一个动点，当△PAC的周长最小时，求点P的坐标；‎ ‎(3)在直线l上是否存在点M，使△MAC为等腰三角形？若存在，直接写出所有符合条件的点M的坐标；若不存在，请说明理由．‎ ‎【答案】解：（1）∵A(－1，0)、B(3，0)经过抛物线y＝ax2＋bx＋c，‎ ‎∴可设抛物线为y＝a（x＋1）（x－3）。‎ 又∵C(0，3) 经过抛物线，∴代入，得3＝a（0＋1）（0－3），即a=－1。‎ ‎∴抛物线的解析式为y＝－（x＋1）（x－3），即y＝－x2＋2x＋3。‎ ‎ （2）连接BC，直线BC与直线l的交点为P。‎ ‎ 则此时的点P，使△PAC的周长最小。‎ 设直线BC的解析式为y＝kx＋b，‎ 将B(3，0)，C(0，3)代入，得：‎ ‎，解得：。‎ ‎∴直线BC的函数关系式y＝－x＋3。‎ 当x－1时，y＝2，即P的坐标(1，2)。‎ ‎（3）存在。点M的坐标为(1，)，(1，－)，(1，1)，(1，0)。‎ ‎【考点】二次函数综合题，待定系数法，曲线上点的坐标与方程的关系，线段中垂线的性质，三角形三边关系，等腰三角形的性质。‎ ‎【分析】（1）可设交点式，用待定系数法求出待定系数即可。‎ ‎ （2）由图知：A、B点关于抛物线的对称轴对称，那么根据抛物线的对称性以及两点之间线段最短可知：若连接BC，那么BC与直线l的交点即为符合条件的P点。‎ ‎（3）由于△MAC的腰和底没有明确，因此要分三种情况来讨论：①MA＝AC、②MA ‎＝MC、②AC＝MC；可先设出M点的坐标，然后用M点纵坐标表示△MAC的三边长，再按上面的三种情况列式求解：‎ ‎∵抛物线的对称轴为： x=1，∴设M(1，m)。‎ ‎∵A(－1，0)、C(0，3)，∴MA2＝m2＋4，MC2＝m2－‎6m＋10，AC2＝10。‎ ‎①若MA＝MC，则MA2＝MC2，得：m2＋4＝m2－‎6m＋10，得：m＝1。‎ ‎②若MA＝AC，则MA2＝AC2，得：m2＋4＝10，得：m＝±。‎ ‎③若MC＝AC，则MC2＝AC2，得：m2－‎6m＋10＝10，得：m＝0，m＝6，‎ 当m＝6时，M、A、C三点共线，构不成三角形，不合题意，故舍去。‎ 综上可知，符合条件的M点，且坐标为(1，)，(1，－)，(1，1)，(1，0)。‎ ‎24. （2012江苏扬州12分）如图1，在平面直角坐标系中，矩形OABC的顶点O在坐标原点，顶点A、C分别在x轴、y轴的正半轴上，且OA＝2，OC＝1，矩形对角线AC、OB相交于E，过点E的直线与边OA、BC分别相交于点G、H．‎ ‎(1)①直接写出点E的坐标：　　．‎ ‎②求证：AG＝CH．‎ ‎(2)如图2，以O为圆心，OC为半径的圆弧交OA与D，若直线GH与弧CD所在的圆相切于矩形内一点F，求直线GH的函数关系式．‎ ‎(3)在(2)的结论下，梯形ABHG的内部有一点P，当⊙P与HG、GA、AB都相切时，求⊙P的半径．‎ ‎【答案】解：（1）① (1，)。‎ ‎②证明：∵四边形OABC是矩形，∴CE＝AE，BC∥OA。∴∠HCE＝∠GAE。‎ ‎∵在△CHE和△AGE中，∠HCE＝∠GAE， CE＝AE，∠HEC＝∠G EA，‎ ‎∴△CHE≌△AGE（ASA）。∴AG＝CH。‎ ‎（2）连接DE并延长DE交CB于M，连接AC，‎ ‎ 则由矩形的性质，点E在AC上。‎ ‎∵DD＝OC＝1＝OA，∴D是OA的中点。‎ ‎∵在△CME和△ADE中，‎ ‎∠MCE＝∠DAE， CE＝AE，∠MEC＝∠DEA，‎ ‎∴△CME≌△ADE（ASA）。∴CM＝AD＝2－1＝1。‎ ‎∵BC∥OA，∠COD＝90°，∴四边形CMDO是矩形。∴MD⊥OD，MD⊥CB。‎ ‎∴MD切⊙O于D。‎ ‎∵HG切⊙O于F，E(1，)，∴可设CH＝HF＝x，FE＝ED＝＝ME。‎ 在Rt△MHE中，有MH2＋ME2＝HE2，即(1－x)2＋()2＝(＋x)2，解得x＝。‎ ‎∴H(，1)，OG＝2－。∴G(，0)。‎ 设直线GH的解析式是：y＝kx＋b，‎ 把G、H的坐标代入得：，解得：。‎ ‎∴直线GH的函数关系式为。‎ ‎（3）连接BG，‎ ‎∵在△OCH和△BAG中，‎ CH=AG，∠HCO＝∠GAB，OC=AB，‎ ‎∴△OCH≌△BAG（SAS）。∴∠CHO＝∠AGB。‎ ‎∵∠HCO＝90°，∴HC切⊙O于C，HG切⊙O于F。‎ ‎∴OH平分∠CHF。∴∠CHO＝∠FHO＝∠BGA。‎ ‎∵△CHE≌△AGE，∴HE＝GE。‎ ‎∵在△HOE和△GBE中，HE＝GE，∠HEO＝∠GEB，OE=BE，‎ ‎∴△HOE≌△GBE（SAS）。∴∠OHE＝∠BGE。21世纪教育网 ‎∵∠CHO＝∠FHO＝∠BGA，∴∠BGA＝∠BGE，即BG平分∠FGA。‎ ‎∵⊙P与HG、GA、AB都相切，∴圆心P必在BG上。‎ 过P做PN⊥GA，垂足为N，则△GPN∽△GBA。∴。‎ 设半径为r，则，解得。‎ 答：⊙P的半径是．‎ ‎【考点】一次函数综合题，矩形的性质和判定，全等三角形的性质和判定，切线的判定和性质，勾股定理，待定系数法，直线上点的坐标与方程的关系，角平分线的判定和性质，相似三角形的判定和性质。‎ ‎【分析】（1）)①根据矩形的性质和边长即可求出E的坐标。‎ ‎ ②推出CE＝AE，BC∥OA，推出∠HCE＝∠EAG，证出△CHE≌△AGE即可。‎ ‎（2）连接DE并延长DE交CB于M，求出DD＝OC＝OA，证△CME≌△ADE，推出四边形CMDO是矩形，求出MD切⊙O于D，设CH＝HF＝x，推出(1－x)2＋()2＝(＋x)2，求出H、G的坐标，设直线GH的解析式是y＝kx＋b，把G、H的坐标代入求出即可。‎ ‎（3）连接BG，证△OCH≌△BAG，求出∠CHO＝∠AGB，证△HOE≌△GBE，求出∠OHE＝∠BGE，得出BG平分∠FGA，推出圆心P必在BG上，过P做PN⊥GA，垂足为N，根据△GPN∽△GBA，得出，设半径为r，代入求出即可。‎ ‎25. （2012江苏镇江9分）对于二次函数和一次函数，把称为这两个函数的“再生二次函数”，其中t是不为零的实数，其图象记作抛物线E。现有点A（2，0）和抛物线E上的点B（－1，n），请完成下列任务：‎ ‎【尝试】‎ ‎（1）当t=2时，抛物线的顶点坐标为 ▲ 。‎ ‎（2）判断点A是否在抛物线E上；‎ ‎（3）求n的值。‎ ‎【发现】通过（2）和（3）的演算可知，对于t取任何不为零的实数，抛物线E总过定点，坐标为 ▲ 。‎ ‎【应用1】二次函数是二次函数和一次函数的一个“再生二次函数”吗？如果是，求出t的值；如果不是，说明理由；‎ ‎【应用2】以AB为边作矩形ABCD，使得其中一个顶点落在y轴上，或抛物线E经过A、B、C、D其中的一点，求出所有符合条件的t的值。‎ ‎【答案】解：【尝试】（1）（1，－2）。‎ ‎ （2）点A在抛物线E上，理由如下：‎ ‎ 将x=2代入得y=0。‎ ‎ ∴点A在抛物线E上。‎ ‎（3）将（－1，n）代入得 ‎ 。‎ ‎【发现】A（2，0）和B（－1，6）。‎ ‎【应用1】不是。‎ ‎ ∵将x=－1代入，得，‎ ‎ ∴二次函数的图象不经过点B。‎ ‎ ∴二次函数不是二次函数和一次函数的一个“再生二次函数”。‎ ‎【应用2】如图，作矩形ABC1D1和ABC2D2，过点B作BK⊥y轴于点K，过点D1作D‎1G⊥x轴于点G，过点C2作C2H⊥y 轴于点H，过点B作BM⊥x轴于点M，C2H与BM相交于点T。‎ 易得AM=3，BM=6，BK=1，△KBC1∽△NBA，‎ 则，即，得。‎ ‎∴C1（0，）。‎ 易得△KBC1≌△GAD1，得AG=1，GD1=。∴D1（3，）。‎ 易得△OAD2∽GAD1，则，‎ 由AG=1，OA=2，GD1=得，得OD2=1。∴D2（0，－1）。‎ 易得△TBC2≌△OD‎2A，得TC2=AO=2，BT==OD2=1。∴C2（－3，5）。‎ ‎∵抛物线E总过定点A、B，∴符合条件的三点只可能是A、B、C或A、B、D。‎ 当抛物线经过A、B、C1时，将C1（0，）代入得；‎ 当抛物线经过A、B、D1时，将D1（3，）代入得；‎ 当抛物线经过A、B、C2时，将C2（－3，5）代入得；‎ 当抛物线经过A、B、D2时，将D2（0，－1）代入得。‎ ‎∴满足条件的所有t值为，，，。‎ ‎【考点】新定义，二次函数的性质，曲线上点的坐标与方程的关系，矩形的性质。‎ ‎【分析】【尝试】（1）当t=2时，抛物线为，∴抛物线的顶点坐标为（1，－2）。‎ ‎ （2）根据点在曲线上，点的坐标满足方程的关系验证即可。‎ ‎ （3）根据点在曲线上，点的坐标满足方程的关系，将（－1，n ‎）代入函数关系式即可求得n的值。‎ ‎【发现】由（1）可得。‎ ‎【应用1】根据点在曲线上，点的坐标满足方程的关系验证即可。‎ ‎【应用2】根据条件，作出矩形，求出各点坐标，根据新定义求出t的值。‎ ‎26. （2012江苏镇江11分）等边△ABC的边长为2，P是BC边上的任一点（与B、C不重合），连接AP，以AP为边向两侧作等边△APD和等边△APE，分别与边AB、AC交于点M、N（如图1）。‎ ‎（1）求证：AM=AN；‎ ‎（2）设BP=x。‎ ①若，BM=，求x的值；‎ ②记四边形ADPE与△ABC重叠部分的面积为S，求S与x之间的函数关系式以及S的最小值；‎ ③连接DE，分别与边AB、AC交于点G、H（如图2），当x取何值时，∠BAD=150？并判断此时以DG、GH、HE这三条线段为边构成的三角形是什么特殊三角形，请说明理由。‎ ‎【答案】解：（1）证明：∵△ABC、△APD和△APE都是等边三角形，‎ ‎ ∴AD=AP，∠DAP=∠BAC=600，∠ADM=∠APN=600。∴∠DAM=∠PAN。‎ ‎ ∴△ADM≌△APN（ASA），∴AM=AN。‎ ‎（2）①易证△BPM∽△CAP，∴，‎ ‎ ∵BN=，AC=2，CP=2－x，∴，即。‎ ‎ 解得x=或x=。‎ ‎ ②四边形AMPN的面积即为四边形ADPE与△ABC重叠部分的面积。‎ ‎ ∵△ADM≌△APN，∴。‎ ‎∴。‎ 如图，过点P作PS⊥AB于点S，过点D作DT⊥AP于点T，则点T是AP的中点。‎ 在Rt△BPS中，∵∠P=600，BP=x，‎ ‎∴PS=BPsin600=x，BS=BPcos600=x。‎ ‎∵AB=2，∴AS=AB－BC=2－x。‎ ‎∴。‎ ‎∴。‎ ‎∴。‎ ‎∴当x=1时，S的最小值为。‎ ③连接PG，设DE交AP于点O。‎ 若∠BAD=150，‎ ‎∵∠DAP =600，∴∠PAG =450。‎ ‎∵△APD和△APE都是等边三角形，‎ ‎∴AD=DP=AP=PE=EA。‎ ‎∴四边形ADPE是菱形。‎ ‎∴DO垂直平分AP。‎ ‎∴GP=AG。∴∠APG =∠PAG =450。‎ ‎∴∠PGA =900。‎ 设BG=t，‎ 在Rt△BPG中，∠B=600，∴BP=2t，PG=。∴AG=PG=。‎ ‎∴，解得t=－1。∴BP=2t=2－2。‎ ‎∴当BP=2－2时，∠BAD=150。‎ 猜想：以DG、GH、HE这三条线段为边构成的三角形是直角三角形。‎ ‎∵四边形ADPE是菱形，∴AO⊥DE，∠ADO=∠AEH=300。‎ ‎∵∠BAD=150，∴易得∠AGO=450，∠HAO=150，∠EAH=450。‎ 设AO=a，则AD=AE=‎2 a，OD=a。∴DG=DO－GO=（－1）a。‎ 又∵∠BAD=150，∠BAC=600，∠ADO=300，∴∠DHA=∠DAH=750。‎ ‎∵DH=AD=‎2a，‎ ‎∴GH=DH－DG=‎2a－（－1）a=（3－）a，‎ HE=2DO－DH=2a－‎2a=2（－1）a。‎ ‎∵，‎ ‎，‎ ‎∴。‎ ‎∴以DG、GH、HE这三条线段为边构成的三角形是直角三角形。‎ ‎【考点】等边三角形的性质，全等三角形的判定和性质，相似三角形的判定和性质，解一元二次方程，锐角三角函数定义，特殊角的三角函数值，二次函数的最值，菱形的判定和性质，勾股定理和逆定理。‎ ‎【分析】（1）由△ABC、△APD和△APE都是等边三角形可得边角的相等关系，从而用ASA证明。‎ ‎ （2）①由△BPM∽△CAP，根据对应边成比例得等式，解方程即可。‎ ‎ ②应用全等三角形的判定和性质，锐角三角函数和勾股定理相关知识求得，‎ 用x的代数式表示S，用二次函数的最值原理求出S的最小值。‎ ‎ ③由∠BAD=150得到四边形ADPE是菱形，应用相关知识求解。‎ ‎ 求出DG、GH、HE的表达式，用勾股定理逆定理证明。‎