中考数学难题解答集锦 7页

经典难题（一）‎ ‎1、已知：如图，O是半圆的圆心，C、E是圆上的两点，CD⊥AB，EF⊥AB，EG⊥CO．‎ 求证：CD＝GF．（初二）‎ A F G C E B O D ‎2、已知：如图，P是正方形ABCD内点，∠PAD＝∠PDA＝150．‎ A P C D B ‎ 求证：△PBC是正三角形．（初二）‎ 假设三角形PBC不是正三角形，则必能在正方形内找 一点Q，使三角形QBC是正三角形 如图，连接QB、QC，‎ 则有QB=AB=QC=CD，角ABQ=DCQ=30度，‎ 角BAQ=BQA=CDQ=CQD=75度 角QAD=QDA=15度 而角PAD=PDA=15度，‎ 从而角QAD与PAD，角QDA与PDA重合，‎ 从而点P与Q重合，三角形PBC与QBC重合 所以三角形PAB是正三角形。‎ ‎3、如图，已知四边形ABCD、A1B‎1C1D1都是正方形，A2、B2、C2、D2分别是AA1、BB1、CC1、DD1的中点．‎ 求证：四边形A2B2C2D2是正方形．（初二）‎ 连接BC1和AB1分别找其中点F,E.连接C2F与A2E并延长相交于Q点，‎ 连接EB2并延长交C2Q于H点，连接FB2并延长交A2Q于G点，‎ 由A2E= A1B1= B1C1= FB2 ，EB2= AB= BC=FC1 ，又∠GFQ+∠Q=900和 ‎∠GEB2+∠Q=900,所以∠GEB2=∠GFQ又∠B2FC2=∠A2EB2 ，‎ 可得△B2FC2≌△A2EB2 ，所以A2B2=B2C2 ， ‎ 又∠GFQ+∠HB2F=900和∠GFQ=∠EB2A2 ,‎ D2‎ C2‎ B2‎ A2‎ D1‎ C1‎ B1‎ C B D A A1‎ 从而可得∠A2B‎2 C2=900 ，‎ 同理可得其他边垂直且相等，‎ 从而得出四边形A2B2C2D2是正方形。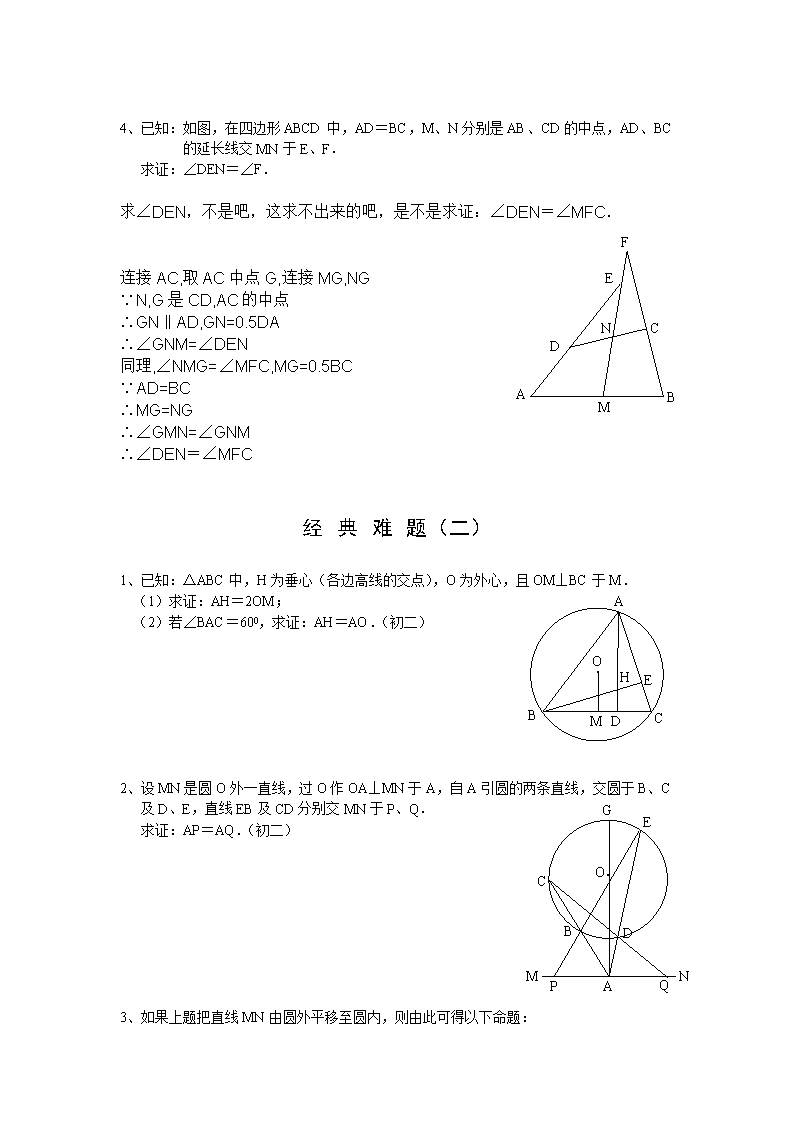‎ ‎4、已知：如图，在四边形ABCD中，AD＝BC，M、N分别是AB、CD的中点，AD、BC的延长线交MN于E、F．‎ 求证：∠DEN＝∠F．‎ 求∠DEN，不是吧，这求不出来的吧，是不是求证：∠DEN＝∠MFC．‎ A N F E C D M B 连接AC,取AC中点G,连接MG,NG ‎∵N,G是CD,AC的中点 ‎∴GN‖AD,GN=0.5DA ‎∴∠GNM=∠DEN 同理,∠NMG=∠MFC,MG=0.5BC ‎∵AD=BC ‎∴MG=NG ‎∴∠GMN=∠GNM ‎∴∠DEN＝∠MFC 经典难题（二）‎ ‎1、已知：△ABC中，H为垂心（各边高线的交点），O为外心，且OM⊥BC于M．‎ ‎·‎ A D H E M C B O ‎　（1）求证：AH＝2OM；‎ ‎　（2）若∠BAC＝600，求证：AH＝AO．（初二）‎ ‎·‎ G A O D B E C Q P N M ‎2、设MN是圆O外一直线，过O作OA⊥MN于A，自A引圆的两条直线，交圆于B、C及D、E，直线EB及CD分别交MN于P、Q．‎ 求证：AP＝AQ．（初二）‎ ‎3、如果上题把直线MN由圆外平移至圆内，则由此可得以下命题：‎ ‎·‎ O Q P B D E C N M ‎·‎ A 设MN是圆O的弦，过MN的中点A任作两弦BC、DE，设CD、EB分别交MN于P、Q．‎ 求证：AP＝AQ．（初二）‎ P C G F B Q A D E ‎4、如图，分别以△ABC的AC和BC为一边，在△ABC的外侧作正方形ACDE和正方形CBFG，点P是EF的中点．‎ 求证：点P到边AB的距离等于AB的一半．（初二）‎ 分别过P、C、E、F作AB的垂线，垂足依次是Q、H、M、N。‎ ‎∵ACDE是正方形，∴∠EAM、∠CAH互余，又∠CAH、∠ACH互余，∴∠EAM＝∠ACH，‎ ‎∵ACDE是正方形，∴AE＝CA，显然有∠AME＝∠CHA＝90°，∴△AEM≌△CAH，∴EM＝AH。‎ ‎∵CBFG是正方形，∴∠FBN、∠CBH互余，又∠FBN、∠BFN互余，∴∠BFN＝∠CBH，‎ ‎∵CBFG是正方形，∴BF＝CB，显然有∠BNF＝∠CHB＝90°，∴△BFN≌△CBH，∴FN＝BH。‎ 由EM＝AH、FN＝BH，得：EM＋FN＝AH＋BH＝AB。‎ 由PQ⊥AB、EM⊥AB、FN⊥AB，得：FN∥PQ∥EM，又EP＝FP，∴PQ是梯形EFNM的中位线，‎ ‎∴由梯形中位线定理，有：PQ＝（EM＋FN）/2，结合证得的EM＋FN＝AB，得：‎ PQ＝AB/2。‎ 经典难题（三）‎ ‎1、如图，四边形ABCD为正方形，DE∥AC，AE＝AC，AE与CD相交于F．‎ A F D E C B 求证：CE＝CF．（初二）‎ 证明：连接BD交AC于点O，过点E作EG⊥AC.‎ ‎∵四边形ABCD是正方形，‎ ‎∴AC=BD，OD=BD/2，∠DOC=90°，∠ACD=45°，‎ ‎∵EG⊥AC，‎ ‎∴∠EGO=90°，‎ ‎∴∠DOC+∠EGO=180°，‎ ‎∴OD//EG，‎ 又∵OG//DE，‎ ‎∴四边形DOGE是矩形，‎ ‎∴DO=EG=BD/2=AC/2，‎ ‎∵AE=AC，‎ ‎∴在Rt△AGE中，EG=AE/2，∠ACE=∠AEC，‎ ‎∴∠EAG=30°，‎ ‎∴∠AEC+∠ACE=180°-∠EAG=180°-30°=150°，‎ ‎∴∠AEC=∠ACE=150°÷2=75°，‎ ‎∴∠ECF=∠ACE-∠ACD=75°-45°=30°，‎ ‎∴∠EFC=180°-∠ECF-∠FEC=180°-30°-75°=75°，‎ ‎∴∠EFC=∠CEF，‎ ‎∴CE＝CF.‎ ‎2、如图，四边形ABCD为正方形，DE∥AC，且CE＝CA，直线EC交DA延长线于F．‎ E D A C B F 求证：AE＝AF．（初二）‎ 过E，D分别做AC的垂线交点为G，H ‎∵AC是正方形ABCD的对角线 ‎∴DH = AC/2‎ ‎∵ED//AC ‎∴EG=DH ‎∵AC = AE ‎∴DH = AE/2‎ ‎∴在Rt△EGC中，∠ECG = 30°‎ ‎∴∠CEA = ∠CAE = 75°‎ ‎∵∠DCA = 45°‎ ‎∴∠DCF = 15°‎ ‎∴∠EFA = ∠DFC = 75° ‎ ‎∴∠EFA = ∠FEA ‎ ‎∴AE = AF ‎ ‎3、设P是正方形ABCD一边BC上的任一点，PF⊥AP，CF平分∠DCE．‎ D A E P C B A 求证：PA＝PF．（初二）‎ 证明：【此题见过，E应为BC延长线上的点】‎ 在AB上截取AG=PC，连接PG ‎∵ABCD是正方形 ‎∴AB=BC，∠B=∠DCB=∠APF=90º【∵PF⊥AP】‎ ‎∵AC=CP ‎∴BG=BP【等量减等量】‎ ‎∴∠BGP=∠BPG=45º ‎∴∠AGP=180º-∠BGP=135º ‎∵CF平分∠DCE ‎∴∠FCE=45º ‎∴∠PCF=180º-∠FCE=135º ‎∴∠AGP=∠PCF ‎∵∠BAP+∠APB=90º ‎ ∠FPC+∠APB=90º ‎∴∠BAP=∠FPC【加上∠AGP=∠PCF，AG=PC】‎ ‎∴⊿AGP≌⊿PCF（ASA）‎ ‎∴PA=PF O D B F A E C P ‎4、如图，PC切圆O于C，AC为圆的直径，PEF为圆的割线，AE、AF与直线PO相交于B、D．求证：AB＝DC，BC＝AD．（初三）‎ 经典难题（四）‎ ‎1、已知：△ABC是正三角形，P是三角形内一点，PA＝3，PB＝4，PC＝5．‎ A P C B 求：∠APB的度数．（初二）‎ ‎2、设P是平行四边形ABCD内部的一点，且∠PBA＝∠PDA．‎ 求证：∠PAB＝∠PCB．（初二）‎ 过点P作DA的平行线，过点A作DP的平行线，两者相交于点E；连接BE ‎ P A D C B 因为DP//AE，AD//PE ‎ 所以，四边形AEPD为平行四边形 ‎ 所以，∠PDA=∠AEP ‎ 已知，∠PDA=∠PBA ‎ 所以，∠PBA=∠AEP ‎ 所以，A、E、B、P四点共圆 ‎ 所以，∠PAB=∠PEB ‎ 因为四边形AEPD为平行四边形，所以：PE//AD，且PE=AD ‎ 而，四边形ABCD为平行四边形，所以：AD//BC，且AD=BC ‎ 所以，PE//BC，且PE=BC ‎ 即，四边形EBCP也是平行四边形 ‎ 所以，∠PEB=∠PCB ‎ 所以，∠PAB=∠PCB ‎3、Ptolemy（托勒密）定理：设ABCD为圆内接凸四边形，求证：AB·CD＋AD·BC＝AC·BD．‎ C B D A ‎　（初三）‎ ‎4、平行四边形ABCD中，设E、F分别是BC、AB上的一点，AE与CF相交于P，且 AE＝CF．求证：∠DPA＝∠DPC．（初二）‎ F P D E C B A 连接DF，DE，过点D做DM⊥CF，DN⊥AE ‎△CFD的面积=1/2平行四边形的面积 ‎△AED的面积=1/2平行四边形的面积 S△CFD=S△AED ‎1/2CF×DM=1/2AE×DN AE=CF DM=DN ‎：∠DPA＝∠DPC．，到角两边距离相等的点在角的平分线上 经典难题（五）‎ ‎1、设P是边长为1的正△ABC内任一点，l＝PA＋PB＋PC，求证：≤l＜2．‎ A P C B ‎　‎ ‎　‎ ‎　‎ ‎　‎ ‎2、已知：P是边长为1的正方形ABCD内的一点，求PA＋PB＋PC的最小值．‎ ‎　‎ ‎　‎ ‎　‎ ‎　‎ ‎　‎ ‎3、P为正方形ABCD内的一点，并且PA＝a，PB＝‎2a，PC＝‎3a，求正方形的边长．‎ A C B P D ‎ ‎ ‎　‎ ‎　　‎ E D C B A ‎4、如图，△ABC中，∠ABC＝∠ACB＝800，D、E分别是AB、AC上的点，∠DCA＝300，∠EBA＝200，求∠BED的度数．‎ ‎　‎ ‎　　‎ A C B P D