中考数学真题矩形菱形正方形 70页

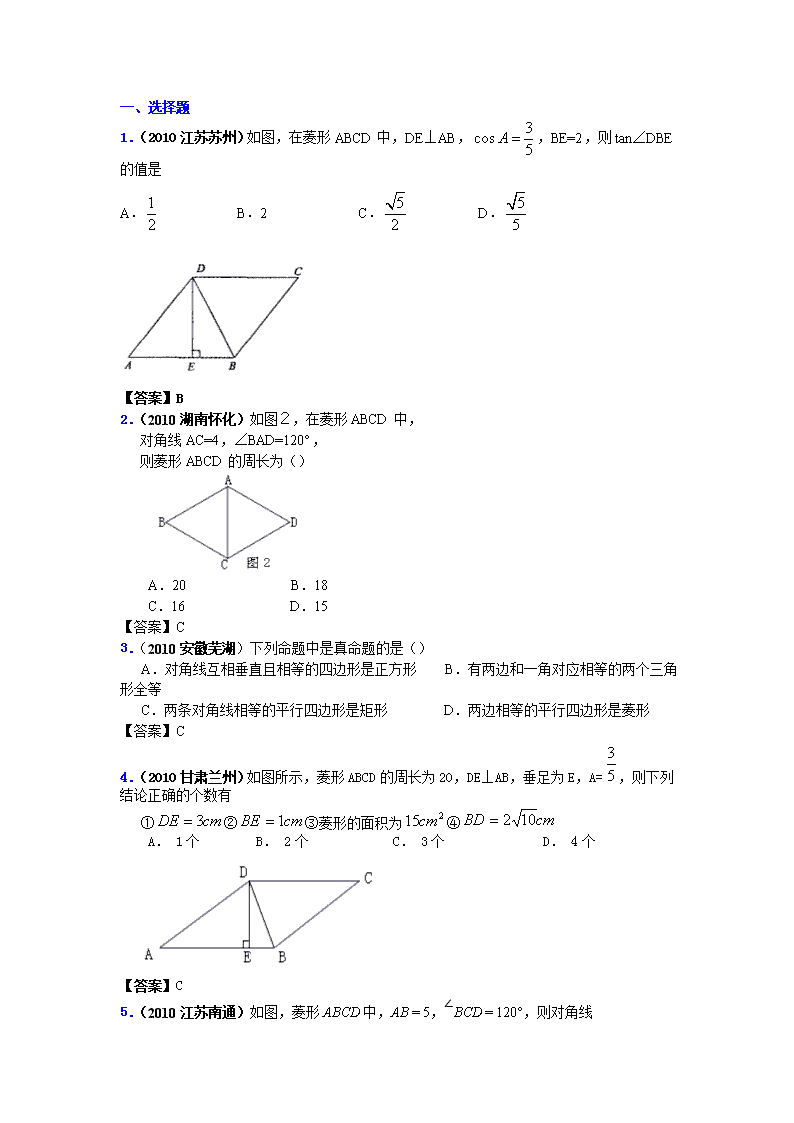
一、选择题 ‎1．（2010江苏苏州）如图，在菱形ABCD中，DE⊥AB，，BE=2，则tan∠DBE的值是 A． B．2 C． D．‎ ‎【答案】B ‎2．（2010湖南怀化）如图２，在菱形ABCD中，‎ 对角线AC=4，∠BAD=120°，‎ 则菱形ABCD的周长为（）‎ A．20 B．18 ‎ C．16 D．15‎ ‎【答案】C ‎3．（2010安徽芜湖）下列命题中是真命题的是（）‎ A．对角线互相垂直且相等的四边形是正方形 B．有两边和一角对应相等的两个三角形全等 C．两条对角线相等的平行四边形是矩形 D．两边相等的平行四边形是菱形 ‎【答案】C ‎4．（2010甘肃兰州）如图所示，菱形ABCD的周长为20，DE⊥AB，垂足为E，A=，则下列结论正确的个数有 ‎①②③菱形的面积为④‎ ‎ A． 1个 B． 2个 C． 3个 D． 4个 ‎【答案】C ‎5．（2010江苏南通）如图，菱形ABCD中，AB = 5，∠BCD = 120°，则对角线 AC的长是 B A C D ‎（第8题）‎ A．20B．15‎ C．10D．5‎ ‎【答案】D ‎6．（2010江苏盐城）如图所示，在菱形ABCD中，两条对角线AC＝6，BD＝8，则此菱形 的边长为 A．5 B．6 C．8 D．10‎ A B C D ‎（第6题）‎ ‎【答案】A ‎7．（2010 浙江省温州）下列命题中，属于假命题的是(▲)‎ ‎ A．三角形三个内角的和等于l80° B．两直线平行，同位角相等 ‎ C．矩形的对角线相等 D．相等的角是对顶角．‎ ‎【答案】D ‎8．（2010 浙江省温州）如图，AC；BD是矩形ABCD的对角线，过点D作DE／／AC交BC的延长线于E，则图中-与AABC全等的 三角形共有(．▲)‎ ‎ A．1个 B．2个 C．3个D．4个 ‎【答案】D ‎9．（2010 浙江义乌）下列说法不正确的是（ ▲ ）‎ A．一组邻边相等的矩形是正方形 B．对角线相等的菱形是正方形 C．对角线互相垂直的矩形是正方形 D．有一个角是直角的平行四边形是正方形 ‎【答案】D ‎10．（2010 重庆）已知：如图，在正方形外取一点，连接 ‎，，．过点作的垂线交于点．‎ 若， ．下列结论：‎ ‎①△≌△；②点到直线的距离为；‎ ‎③；④；⑤．‎ ‎10题图 其中正确结论的序号是（ ）‎ A．①③④ B．①②⑤C．③④⑤D．①③⑤‎ ‎【答案】D ‎11．（2010山东聊城）如图，点P是矩形ABCD的边AD的一个动点，矩形的两条边AB、BC的长分别为3和4，那么点P到矩形的两条对角线AC和BD的距离之和是（ ）‎ A．　　 B．　 C．　　 D．不确定 ‎【答案】A ‎12．（2010 福建晋江）如图，将一张正方形纸片剪成四个小正方形，得到4个小正方形，称为第一次操作；然后，将其中的一个正方形再剪成四个小正方形，共得到7个小正方形，称为第二次操作；再将其中的一个正方形再剪成四个小正方形，共得到10个小正方形，称为第三次操作；...，根据以上操作，若要得到2011个小正方形，则需要操作的次数是( ) .‎ 第7题图 A. 669 B. 670　 C.671 D. 672‎ ‎【答案】B ‎13．（2010 山东济南） 如图所示，两个全等菱形的边长为1厘米，一只蚂蚁由点开始按的顺序沿菱形的边循环运动，行走2010厘米后停下，则这只蚂蚁停在点．‎ C A F D E B G ‎【答案】C ‎14．（2010 江苏连云港）如图，四边形ABCD的对角线AC、BD互相垂直，则下列条件能判定四边形ABCD为菱形的是（ ）‎ A B C D 第7题 A．BA＝BC B．AC、BD互相平分 C．AC＝BD D．AB∥CD ‎【答案】B ‎15．（2010福建宁德）如图所示，如果将矩形纸沿虚线①对折后，沿虚线②剪开，剪出一个 直角三角形，展开后得到一个等腰三角形.则展开后三角形的周长是（ ）.‎ ‎①‎ ‎②‎ ‎3‎ ‎4‎ ‎10‎ A．2＋ B．2＋2 C．12 D．18‎ ‎【答案】B ‎16．（2010江西）如图，已知矩形纸片ABCD，点E 是AB的中点，点G是BC上的一点，∠BEG>60°，现沿直线EG将纸片折叠，使点B落在纸片上的点H处，连接AH，则与∠BEG相等的角的个数为( )‎ A．4 B．3 C．2 D．1‎ B A G C D H E ‎(第8题图)‎ ‎【答案】B ‎17．（2010 山东滨州）如图,把一个长方形纸片对折两次,然后剪下一个角.为了得到一个正方形,剪刀与折痕所成的角的度数应为( ) ‎ A.60° B.30° C.45° D.90°‎ ‎【答案】C ‎18．（2010山东潍坊）如图，已知矩形ABCD，一条直线将该矩形ABCD分割成两个多边形（含三角形），若这两个多边形的内角和分别为M和N，则M＋N不可能是（ ）．‎ ‎【答案】D ‎19．（2010北京） 若菱形两条对角线的长分别为6和8，则这个菱形的周长为（ ）‎ A．20 B．16 C．12 D． 10‎ ‎【答案】A ‎20．（2010 浙江省温州）下列命题中，属于假命题的是(▲)‎ ‎ A．三角形三个内角的和等于l80° B．两直线平行，同位角相等 ‎ C．矩形的对角线相等 D．相等的角是对顶角．‎ ‎【答案】D ‎21．（2010 浙江义乌）下列说法不正确的是（ ▲ ）‎ A．一组邻边相等的矩形是正方形 B．对角线相等的菱形是正方形 C．对角线互相垂直的矩形是正方形 D．有一个角是直角的平行四边形是正方形 ‎【答案】D ‎22．（2010陕西西安）若一个菱形的边长为2，则这个菱形两条对角线长的平方和为 ‎ A．16 B．8 C．4 D．1‎ ‎【答案】A ‎23．（2010江西省南昌）如图，已知矩形纸片，点是的中点，点是上的一点，‎ ‎，现沿直线将纸片折叠，使点落在约片上的点处，‎ 连接，则与相等的角的个数为 ( )‎ A.4 B. 3 C.2 D.1‎ ‎ （第10题）‎ ‎【答案】B ‎24．（2010湖北襄樊）下列命题中，真命题有（ ）‎ ‎ （1）邻补角的平分线互相垂直 （2）对角线互相垂直平分的四边形是正方形 ‎ （3）四边形的外角和等于360° （4）矩形的两条对角线相等 A．1个 B．2个 C．3个 D．4个 ‎【答案】C ‎25．（2010湖北襄樊）菱形的周长为8cm，高为1cm，则菱形两邻角度数比为（ ）‎ A．3：1 B．4：1 C．5：1 D．6：1 ‎ ‎【答案】C ‎26．（2010 四川泸州）如图1，四边形ABCD是正方形，E是边CD上一点，若△AFB经过逆时针旋转角θ后与△AED重合，则θ的取值可能为（ ）‎ A．90° B．60° C．45° D．30°‎ ‎【答案】A ‎27．（2010 山东淄博）如图所示，把一长方形纸片沿MN折叠后，点D，C分别落在D′，C′的位置．若∠AMD′＝36°，则∠NFD′等于 ‎（A）144°A B C D D′‎ C′‎ N M F ‎(第10题)‎ （B）126°‎ ‎（C）108° （D）72°‎ ‎【答案】B ‎28．（2010 天津）下列命题中正确的是 ‎（A）对角线相等的四边形是菱形 ‎ ‎（B）对角线互相垂直的四边形是菱形 ‎（C）对角线相等的平行四边形是菱形 ‎（D）对角线互相垂直的平行四边形是菱形 ‎【答案】D ‎29．（2010 湖南湘潭）下列说法中,你认为正确的是 A．四边形具有稳定性 B．等边三角形是中心对称图形 C．任意多边形的外角和是360o D．矩形的对角线一定互相垂直 ‎【答案】C ‎30．（2010 福建泉州南安）已知四边形中，，如果添加 一个条件，即可推出该四边形是正方形，那么这个条件可以是（）．‎ A． B． C． D．‎ ‎【答案】D ‎31．（2010 四川自贡）边长为1的正方形ABCD绕点A逆时针旋转30°得到正方形AB′‎ C′D′，两图叠成一个“蝶形风筝”（如图所示阴影部分），则这个风筝的面积是（ ）。‎ A．2－ B．‎ C．2－ D．2 ‎ ‎【答案】A ‎32．（2010 山东荷泽）如图，矩形纸片ABCD中，AB＝4，AD＝3，折叠纸片使AD边与对角线BD重合，折痕为DG，记与点A重合点为A＇，则△A＇BG的面积与该矩形的面积比为 A． B． C． D．‎ A B C D G A＇‎ ‎【答案】C ‎33．（2010 山东荷泽） 如图，菱形ABCD中，∠B＝60°，AB＝2㎝，E、F分别是BC、CD的中点，连结AE、EF、AF，则△AEF的周长为 A．㎝ B．㎝ C．㎝ D．3㎝ ‎8题图 A B C D E F ‎【答案】B ‎34．（2010青海西宁） 矩形ABCD中，E、F、M为AB、BC、CD边上的点，且AB=6,BC=7,AE=3,DM=2,EF⊥FM,则EM的长为 A．5 B． C．6 D．‎ ‎【答案】B ‎35．（2010广西南宁）正方形、正方形和正方形的位置如图所示，点在线段上，正方形的边长为4，则 的面积为：‎ ‎（A）10 （B）12 （C）14 （D）16‎ ‎【答案】D ‎36．（2010广东茂名）如图，边长为1的正方形ABCD绕点A逆时针旋转45度后得到正方形，边与DC交于点O，则四边形的周长是 A． B． C． D．‎ ‎(第10题图)‎ ‎【答案】A ‎37．（2010广西柳州）如图4，在正方形ABCD的外侧作等边△ADE，则∠AEB的度数为 ‎ A．10° B．12.5° C．15° D．20°‎ ‎【答案】C ‎38．（2010广西柳州）如图6，四边形ABCD是边长为9的正方形纸片，将其沿MN折叠，使点B落在CD边上的处，点A对应点为，且=3，则AM的长是 ‎ A．1.5 B．2 C．2.25 D．2.5‎ A BA CA D]‎ CA MA NA 图6‎ ‎【答案】B ‎39．（2010湖北宜昌）如图，菱形ABCD中，AB=15,°，则B、D两点之间的距离为（ ）。‎ ‎40．（2010广西河池）如图5是用4个全等的直角三角形与1个小正方形镶嵌而成的 正方形图案，已知大正方形面积为49，小正方形面积为4，若用 ‎，表示直角三角形的两直角边（），下列四个说法：‎ ‎①，②，③，④.‎ 其中说法正确的是【】‎ A．①② B. ①②③ C. ①②④ D. ①②③④‎ 图5‎ ‎【答案】B ‎41．（2010广东肇庆）菱形的周长为4，一个内角为60°，则较短的对角线长为( )‎ A．2 B． C．1 D． ‎【答案】C ‎42．（2010吉林）如图，在矩形ABCD中，AB=12cm，BC=6cm，点E、F分别在AB、CD上，将矩形ABCD沿EF折叠，使点A、D分别落在矩形ABCD外部的点A’，D’处，则整个阴影部分图形的周长为（ ）‎ A．18cm B．36cm C．40cm D．72cm ‎【答案】B ‎ （第13题）‎ A.15‎ B.‎ C.7.5‎ D.15‎ ‎【答案】A 二、填空题 ‎1．（2010江苏盐城）小明尝试着将矩形纸片ABCD（如图①，AD>CD）沿过A点的直线折叠，使得B点落在AD边上的点F处，折痕为AE（如图②）；再沿过D点的直线折叠，使得C点落在DA边上的点N处，E点落在AE边上的点M处，折痕为DG（如图③）．如果第二次折叠后，M点正好在∠NDG的平分线上，那么矩形ABCD长与宽的比值为▲．‎ A B C D A B C D E F ‎①‎ ‎②‎ A B C D E G M N ‎③‎ ‎【答案】 ‎2．（2010山东威海）从边长为a的大正方形纸板中间挖去一个边长为b的小正方形后，将其截成四个相同的等腰梯形﹙如图①﹚，可以拼成一个平行四边形﹙如图②﹚． ‎ 现有一平行四边形纸片ABCD﹙如图③﹚，已知∠A＝45°，AB＝6，AD＝4．若将该纸片按图②方式截成四个相同的等腰梯形，然后按图①方式拼图，则得到的大正方形的面积为． ‎ 图 ②‎ 图 ①‎ a b A 图 ③‎ B C D ‎（第18题图）‎ ‎【答案】．‎ ‎3．（2010浙江嘉兴）如图，已知菱形ABCD的一个内角，对角线AC、BD相交于点O，点E在AB上，且，则=　　▲　　度．‎ ‎（第15题）‎ ‎【答案】25‎ ‎4．（2010年上海）已知正方形ABCD中，点E在边DC上，DE = 2，EC = 1（如图4所示） 把线段AE绕点A旋转，使点E落在直线BC上的点F处，则F、C两点的距离为___________.‎ 图4‎ ‎【答案】CF=1或5‎ ‎5．（2010山东青岛）把一张矩形纸片（矩形ABCD）按如图方式折叠，使顶点B和点D重合，折痕为EF．若AB= 3cm，BC= 5cm，则重叠部分△DEF的面积是cm2．‎ A B C F E ‎′‎ 第13题图 ‎（）‎ D ‎【答案】5.1‎ ‎6．（2010 福建德化）已知菱形的两对角线长分别为6㎝和8㎝，则菱形的面积为㎝2.‎ ‎【答案】24‎ ‎7．（2010湖南邵阳）如图（九）在等腰梯形ABCD中，AB∥DC，AD=BC=CD，点E为AB上一点，连结CE，请添加一个你认为合适的条件，使四边形AECD为菱形．‎ ‎ 图（九）‎ ‎【答案】AE＝CD或AD∥CE或CE=BC或∠CEB＝∠B的任意一个都可 ‎8．（2010山东临沂） 正方形的边长为,点、分别是对角线上的两点，过点、分别作、的平行线，如图所示，则图中阴影部分的面积之和等于.‎ ‎（第18题图）‎ ‎【答案】‎ ‎9．（2010四川宜宾）如图，点P是正方形ABCD的对角线BD上一点，PE⊥BC于点E，PF ‎⊥CD于点F，连接EF给出下列五个结论：①AP=EF；②AP⊥EF；③△APD一定是等腰三角形；‎ ‎④∠PFE=∠BAP；⑤PD=EC．其中正确结论的序号是．‎ ‎【答案】①、②、④、⑤．‎ ‎10．（2010 江苏连云港）矩形纸片ABCD中，AB＝3，AD＝4，将纸片折叠，使点B落在边CD上的B’处，折痕为AE．在折痕AE上存在一点P到边CD的距离与到点B的距离相等，则此相等距离为________．‎ 第18题 AD BAD CFEBAD B’‎ D E P ‎【答案】‎ ‎11．（2010 黄冈）如图矩形纸片ABCD，AB＝5cm，BC＝10cm，CD上有一点E，ED＝2cm，AD上有一点P，PD＝3cm，过P作PF⊥AD交BC于F，将纸片折叠，使P点与E点重合，折痕与PF交于Q点，则PQ的长是____________cm.‎ ‎【答案】‎ ‎12．（2010 河北）把三张大小相同的正方形卡片A，B，C叠放在一个底面为正方形的盒底上，底面未被卡片覆盖的部分用阴影表示．若按图10-1摆放时，阴影部分的面积为S1；若按图10-2摆放时，阴影部分的面积为S2，则S1S2（填“＞”、“＜”或“=”）．‎ 图10-1‎ A C B C B A 图10-2‎ ‎【答案】=‎ ‎13．（2010 山东省德州）在四边形中，点E，F，G，H分别是边AB，BC，CD，DA的中点，如果四边形EFGH为菱形，那么四边形ABCD是（只要写出一种即可）．‎ ‎【答案】答案不唯一：只要是对角线相等的四边形均符合要求．‎ 如：正方形、矩形、等腰梯形等．‎ ‎14．2010 广东珠海）如图，P是菱形ABCD对角线BD上一点，PE⊥AB于点E，PE＝4cm，‎ 则点P到BC的距离是_____cm. ‎ ‎【答案】4‎ ‎15．（2010 四川巴中）如图5所示，已知□ABCD，下列条件：①AC=BD，②AB=AD，③∠1=∠2，④AB⊥BC中，能说明□ABCD是矩形的有（填写番号）。‎ 图5‎ ‎【答案】①④‎ ‎16．（2010江苏淮安）已知菱形ABCD中,对角线AC=8cm，BD=6cm，在菱形内部(包括边界)任取一点P，使△ACP的面积大于6 cm2的概率为．‎ ‎【答案】‎ ‎17．（2010 湖南株洲）如图，四边形是菱形，对角线和相交于点，，，则这个菱形的面积是．‎ 第14题图 ‎【答案】16‎ ‎18．（2010广东中山）如图（1），已知小正方形ABCD的面积为1，把它的各边延长一倍得到新正方形；把正方形边长按原法延长一倍得到正方形 ‎（如图（2））；以此下去，则正方形的面积为．‎ ‎【答案】625‎ ‎19．(2010江苏苏州)如图，四边形ABCD是正方形，延长AB到E，‎ ‎ 使AE=AC，则∠BCE的度数是▲°．‎ ‎【答案】22.5‎ ‎20．（2010湖北恩施自治州）如图，在矩形ABCD中，AD =4，DC =3，将△ADC按逆时针方向绕点A旋转到△AEF（点A、B、E在同一直线上），连结CF，则CF =.‎ ‎【答案】5‎ ‎21．（2010山东泰安）如图，将矩形纸片ABCD沿EF折叠，使D点与BC边的中点D/重合，若BC=8，CD=6，则CF=.‎ ‎【答案】‎ ‎22．（2010云南楚雄）如图，在□ABCD中，对角线与相交于点，在不添加任何辅助线和字母的情况下，请添加一个条件，使得□ABCD变为矩形，需要添加的条件是．（写出一个即可）‎ ‎【答案】AC＝BD或∠ABC＝90°等．‎ ‎23．（2010湖北随州）如图矩形纸片ABCD，AB＝5cm，BC＝10cm，CD上有一点E，ED＝2cm，AD上有一点P，PD＝3cm，过P作PF⊥AD交BC于F，将纸片折叠，使P点与E点重合，折痕与PF交于Q点，则PQ的长是____________cm.‎ ‎【答案】‎ ‎24．（2010黑龙江哈尔滨）如图，将矩形纸片ABC（D）折叠，使点（D）与点B重合，点C落在点处，折痕为EF，若，那么的度数为度。‎ ‎【答案】125‎ ‎25．（2010广东东莞）如图⑴，已知小正方形ABCD的面积为1，把它的各边延长一倍得到新正方形A1B1C1D1；把正方形A1B1C1D1边长按原法延长一倍后得到正方形A2B2C2D2（如图⑵）；以此下去…，则正方形A4B4C4D4的面积为．‎ A B C D A1‎ B1‎ C1‎ D1‎ 第10题图（1）‎ C D A1‎ B1‎ C1‎ D1‎ A B A2‎ B2‎ C2‎ D2‎ 第10题图（2）‎ ‎【答案】625‎ ‎26．（2010 四川绵阳）已知菱形ABCD的两条对角线相交于点O，若AB = 6，∠BDC =‎ ‎ 30°，则菱形的面积为．‎ ‎【答案】18‎ ‎27．（2010广东汕头）如图（1），已知小正方形ABCD的面积为1，把它的各边延长一倍得到新正方形A1B1C1D1；把正方形A1B1C1D1边长按原法延长一倍得到正方形A2B2C2D2（如图（2））；以此下去···，则正方形A4B4C4D4的面积为__________‎ 第13题图（1）‎ A1‎ B1‎ C1‎ D1‎ A B C D D2‎ A2‎ B2‎ C2‎ D1‎ C1‎ B1‎ A1‎ A B C D 第13题图（2）‎ ‎【答案】625‎ ‎28．（2010 山东淄博）在一块长为8、宽为的矩形中，恰好截出三块形状相同、大小不等的直角三角形，且三角形的顶点都在矩形的边上．其中面积最小的直角三角形的较短直角边的长是．‎ ‎【答案】2‎ ‎29．（2010 天津）如图，已知正方形的边长为3，为边上一点， ‎ ‎．以点为中心，把△顺时针旋转，得 ‎△，连接，则的长等于．‎ 第（14）题 E A D B C ‎【答案】‎ ‎30．（2010 甘肃）如图，在中，点D、E、F分别在边、、上，且 ‎，．下列四种说法：‎ ‎①四边形是平行四边形；‎ ‎②如果，那么四边形是矩形；‎ ‎③如果平分，那么四边形是菱形；‎ ‎④如果且，那么四边形是菱形.‎ 其中，正确的有.（只填写序号）‎ Ａ Ｆ Ｃ Ｄ Ｂ Ｅ 第18题图 ‎【答案】①②③④‎ ‎31．（2010 福建泉州南安）如图，大正方形网格是由25个边长为1的小正方形组成，‎ 把图中阴影部分剪下来，用剪下来的阴影部分拼成一个正方形，‎ 那么新正方形的边长是．‎ ‎（第16题图）‎ ‎【答案】‎ ‎32．（2010广西梧州）如图3，边长为6的正方形ABCD绕点B按顺时针方向旋转30°后得到正方形EBGF，EF交CD于点H，则FH的长为______（结果保留根号）。‎ 图3‎ A B C D F E H G ‎【答案】6-2‎ ‎33．（2010广西河池）如图2，矩形ABCD中，AB＝8cm，BC＝4cm，E是DC的 中点，BF＝BC，则四边形DBFE的面积为．‎ C D E F B A 图2‎ ‎【答案】10‎ ‎34．（2010贵州铜仁）已知菱形的两条对角线的长分别为5和6，则它的面积是________．‎ ‎【答案】15‎ ‎35．（2010云南曲靖）如图，活动衣帽架由三个菱形组成，利用四边形的不稳定性，调整菱形的内角，使衣帽架拉伸或收缩，当菱形的边长为18cm，=1200时，A、B两点的距离为cm.‎ ‎【答案】54‎ ‎36．（2010黑龙江绥化）如图所示，E、F是矩形ABCD对角线AC上的两点，试添加一个条件：，使得△ADF≌△CBE．‎ ‎【答案】AF=CE或AE=CF或DF∥BE或∠ABE=∠CDF等 ‎37．（2010黑龙江绥化）如图，在平面直角坐标系中，边长为1的正方形OA1B1C的对角线 A1C和OB1交于点M1；以M1A1为对角线作第二个正方形A2A1B2M1，对角线A1M1和A2B2交于点M2；以M2A1为对角线作第三个正方形A3A1B3M2，对角线A1M2和A3B3交于点M3；……依此类推，这样作的第n 个正方形对角线交点Mn的坐标为.‎ ‎【答案】‎ ‎38．（2010内蒙呼和浩特）如图，矩形ABCD沿着直线BD折叠，使点C落在处，交AD 于点E，AD = 8，AB = 4，则DE的长为．‎ ‎【答案】5‎ 三、解答题 ‎1．（2010安徽省中中考）如图，AD∥FE，点B、C在AD上，∠1＝∠2，BF＝BC ‎⑴求证：四边形BCEF是菱形 ‎⑵若AB＝BC＝CD，求证：△ACF≌△BDE ‎【答案】‎ ‎2．（10湖南益阳）如图7，在菱形ABCD中，∠A=60°,=4,O为对角线BD的中点，过O点作OE⊥AB，垂足为E．‎ ‎(1) 求∠ABD 的度数；‎ ‎ (2)求线段的长．‎ ‎【答案】解:⑴　在菱形中,，‎ ‎∴为等边三角形 ‎ ‎∴……………………………4分 ‎⑵由（1）可知 又∵为的中点 ‎∴……………………………6分 又∵，及 ‎∴‎ ‎∴……………………………8分 ‎3．（10湖南益阳）我们把对称中心重合，四边分别平行的两个正方形之间的部分叫“方形环”，易知方形环四周的宽度相等.‎ 一条直线l与方形环的边线有四个交点、、、．小明在探究线段与 的数量关系时，从点、向对边作垂线段、，利用三角形全等、相似及锐角三角函数等相关知识解决了问题．请你参考小明的思路解答下列问题：‎ ‎⑴当直线l与方形环的对边相交时（如图），直线l分别交、、、于、、、，小明发现与相等，请你帮他说明理由；‎ ‎⑵当直线l与方形环的邻边相交时（如图），l分别交、、、于、、、，l与的夹角为，你认为与还相等吗？若 相等，说明理由；若不相等，求出的值（用含的三角函数表示）.‎ ‎【答案】‎ ‎⑴解: 在方形环中，‎ ‎∵∥‎ ‎∴‎ ‎∴△≌△‎ ‎∴……………………………5分 ‎⑵解法一：∵‎ ‎∴∽……………………………8分 ‎∴‎ ‎∵‎ ‎∴ （或）……………………………10分 ‎①当时，tan=1,则 ‎②当时，‎ ‎ 则 （或）……………………………12分 解法二：在方形环中，‎ ‎ 又∵‎ ‎∴∥‎ ‎∴‎ ‎ 在与中，‎ ‎ 即 （或）……………………………10分 ‎①当时，‎ ‎②当时，‎ ‎ 则 （或）……………………………12分 ‎4．（2010江苏南京）（8分）如图，正方形ABCD的边长是2，M是AD的中点，点E从点A出发，沿AB运动到点B停止，连接EM并延长交射线CD于点F，过M作EF的垂线交射线BC于点G，连结EG、FG。‎ ‎（1）设AE=时，△EGF的面积为，求关于的函数关系式，并写出自变量的取值范围；‎ ‎（2）P是MG的中点，请直接写出点P的运动路线的长。‎ ‎【答案】‎ ‎5．（2010辽宁丹东市） 如图，已知矩形ABCD中，E是AD上的一点，F是AB上的一点，EF⊥EC，且EF=EC，DE=4cm，矩形ABCD的周长为32cm，求AE的长．‎ 第20题图 B C A E D F ‎【答案】解：在Rt△AEF和Rt△DEC中， ∵EF⊥CE， ∴∠FEC=90°， ‎ ‎∴∠AEF+∠DEC=90°，而∠ECD+∠DEC=90°，‎ ‎∴∠AEF=∠ECD． 3分 又∠FAE=∠EDC=90°．EF=EC ‎∴Rt△AEF≌Rt△DCE． 5分 AE=CD． 6分 AD=AE+4．‎ ‎∵矩形ABCD的周长为32 cm， ‎ ‎∴2（AE+AE+4）=32． 8分 解得， AE=6 （cm）． 10分 ‎6．（2010山东济宁）‎(第22题)‎ 数学课上，李老师出示了这样一道题目：如图，正方形的边长为，为边延长线上的一点，为的中点，的垂直平分线交边于，交边的延长线于.当时，与的比值是多少？‎ 经过思考，小明展示了一种正确的解题思路：过作直线平行于交，分别于，，如图，则可得：，因为，所以.可求出和的值，进而可求得与的比值.‎ ‎(1) 请按照小明的思路写出求解过程.‎ ‎(2) 小东又对此题作了进一步探究，得出了的结论.你认为小东的这个结论正确吗？如果正确，请给予证明；如果不正确，请说明理由.‎ ‎【答案】‎ ‎（1）解：过作直线平行于交，分别于点，，‎ 则，，.‎ ‎∵，∴. 2分 ‎∴，.‎ ‎∴. 4分 ‎（2）证明：作∥交于点，5分 则，.‎ ‎∵，‎ ‎∴.‎ ‎∵，，‎ ‎∴.∴. 7分 ‎∴. 8分‎(第22题)‎ ‎7．（2010山东青岛）已知：如图，在正方形ABCD中，点E、F分别在BC和CD上，AE= AF．‎ ‎（1）求证：BE= DF；‎ ‎（2）连接AC交EF于点O，延长OC至点M，使OM= OA，连接EM、FM．判断四边形AEMF是什么特殊四边形？并证明你的结论．‎ ‎【答案】‎ 证明：（1）∵四边形ABCD是正方形，‎ ‎∴AB＝AD,∠B=∠D=90°．‎ ‎∵AE = AF，‎ ‎∴．‎ ‎∴BE＝DF．4分 A D B E F O C M 第21题图 ‎（2）四边形AEMF是菱形．‎ ‎∵四边形ABCD是正方形，‎ ‎∴∠BCA = ∠DCA = 45°，BC = DC．‎ ‎∵BE＝DF，‎ ‎∴BC－BE = DC－DF. 即．‎ ‎∴．‎ ‎∵OM = OA，‎ ‎∴四边形AEMF是平行四边形．‎ ‎∵AE = AF，‎ ‎∴平行四边形AEMF是菱形． 8分 ‎8．（2010山东日照）如图，四边形ABCD是边长为a的正方形，点G，E分别是边AB，BC的中点，∠AEF=90o，且EF交正方形外角的平分线CF于点F．‎ ‎ （1）证明：∠BAE=∠FEC；‎ ‎（2）证明：△AGE≌△ECF；‎ ‎（3）求△AEF的面积．‎ ‎【答案】‎ ‎（1）证明：∵∠AEF=90o，‎ ‎∴∠FEC+∠AEB=90o．………………………………………1分 在Rt△ABE中，∠AEB+∠BAE=90o，‎ ‎∴∠BAE=∠FEC；……………………………………………3分 ‎（2）证明：∵G，E分别是正方形ABCD的边AB，BC的中点，‎ ‎∴AG=GB=BE=EC，且∠AGE=180o－45o=135o．‎ 又∵CF是∠DCH的平分线，‎ ‎∠ECF=90o+45o=135o．………………………………………4分 在△AGE和△ECF中，‎ ‎∴△AGE≌△ECF； …………………………………………6分 ‎ （3）解：由△AGE≌△ECF，得AE=EF．‎ 又∵∠AEF=90o，‎ ‎∴△AEF是等腰直角三角形．………………………………7分 由AB=a，BE=a，知AE=a，‎ ‎∴S△AEF=a2．…………………………………………………9分 ‎9．（2010四川眉山）如图，O为矩形ABCD对角线的交点，DE∥AC，CE∥BD．‎ ‎（1）试判断四边形OCED的形状，并说明理由；‎ ‎（2）若AB=6，BC=8，求四边形OCED的面积．‎ ‎【答案】‎ 解：（1）四边形OCED是菱形．…………（2分）‎ ‎∵DE∥AC，CE∥BD，‎ ‎∴四边形OCED是平行四边形，…………（3分）‎ 又 在矩形ABCD中，OC=OD，‎ ‎∴四边形OCED是菱形．…………………（4分） ‎ ‎（2）连结OE．由菱形OCED得：CD⊥OE， …………（5分）‎ ‎∴OE∥BC ‎ 又 CE∥BD ‎∴四边形BCEO是平行四边形 ‎∴OE=BC=8……………………………………………（7分）‎ ‎∴S四边形OCED=……………（8分）‎ ‎10．（2010浙江宁波）如图1，有一张菱形纸片ABCD，AC=8， BD=6.‎ ‎ (1)请沿着AC剪一刀，把它分成两部分，把剪开的两部分拼成一 ‎ 个平行四边形，在图2中用实线画出你所拼成的平行四边形；若 ‎ 沿着BD剪开，请在图3中用实线画出拼成的平行四边形.并直接 ‎ 写出这两个平行四边形的周长.‎ ‎(图1)‎ ‎ (2)沿着一条直线剪开，拼成与上述两种都不全等的平行四边形，‎ ‎ 请在图4中用实线画出拼成的平行四边形.‎ ‎ (注：上述所画的平行四边形都不能与原菱形全等)‎ ‎(图4)‎ ‎(图3)‎ ‎(图2)‎ 周长为 ▲ ‎ 周长为 ▲ ‎ ‎(第21题)‎ ‎【答案】‎ 解：(1)‎ ‎ 1分 ‎ ‎ 周长为26 2分 ‎ 3分 ‎ 周长为22 4分 ‎ (2)‎ ‎ 6分 ‎ 注:画法不唯一.‎ ‎11．（2010浙江绍兴） (1) 如图1,在正方形ABCD中,点E,F分别在边BC,‎ CD上,AE,BF交于点O,∠AOF＝90°.‎ 求证：BE＝CF.‎ 第23题图1‎ ‎(2) 如图2,在正方形ABCD中,点E,H,F,G分别在边AB,‎ BC,CD,DA上,EF,GH交于点O,∠FOH＝90°, EF ‎＝4.求GH的长.‎ 第23题图2‎ ‎(3) 已知点E,H,F,G分别在矩形ABCD的边AB,BC,CD,DA上，EF,GH交于点O,‎ ‎∠FOH＝90°,EF＝4. 直接写出下列两题的答案：‎ ‎①如图3,矩形ABCD由2个全等的正方形组成,求GH的长；‎ ‎②如图4,矩形ABCD由n个全等的正方形组成,求GH的长(用n的代数式表示).‎ 第23题图4‎ 第23题图3‎ ‎【答案】‎ 第23题图1‎ ‎(1) 证明：如图1，∵ 四边形ABCD为正方形，‎ ‎∴AB=BC,∠ABC=∠BCD=90°，‎ ‎∴∠EAB+∠AEB=90°.‎ ‎∵∠EOB=∠AOF＝90°,‎ ‎∴∠FBC+∠AEB=90°，∴∠EAB=∠FBC，‎ ‎∴△ABE≌△BCF ， ∴BE=CF．‎ 第23题图2‎ O′‎ N M ‎(2) 解：如图2,过点A作AM//GH交BC于M，‎ 过点B作BN//EF交CD于N,AM与BN交于点O/，‎ 则四边形AMHG和四边形BNFE均为平行四边形， ‎ ‎∴EF=BN,GH=AM，‎ ‎∵∠FOH＝90°, AM//GH，EF//BN, ∴∠NO/A=90°,‎ 故由(1)得, △ABM≌△BCN，∴AM=BN，‎ ‎∴GH=EF=4．‎ ‎(3) ① 8．② 4n． ‎ ‎12．（2010 浙江省温州市）(本题10分)如图，在□ABCD中，EF∥BD，分别交BC，CD于点P，Q，交AB，AD的延长线于点E．F．已知BE=BP．‎ ‎ 求证：(1)∠E=∠F(2)□ABCD是菱形．‎ ‎【答案】‎ ‎13．（2010重庆市潼南县）(10分) 如图,四边形ABCD是边长为2的正方形，点G是BC延长线上一点，连结AG，点E、F分别在AG上，连接BE、DF，∠1=∠2 ， ∠3=∠4.‎ ‎（1）证明：△ABE≌△DAF；‎ ‎（2）若∠AGB=30°，求EF的长.‎ ‎【答案】解：（1）∵四边形ABCD是正方形 ‎ ‎∴AB=AD 在△ABE和△DAF中 ‎∴△ABE≌△DAF-----------------------4分 ‎（2）∵四边形ABCD是正方形 ‎∴∠1+∠4=900‎ ‎∵∠3=∠4‎ ‎∴∠1+∠3=900‎ ‎∴∠AFD=900----------------------------6分 在正方形ABCD中， AD∥BC ‎∴∠1=∠AGB=300‎ 在Rt△ADF中，∠AFD=900 AD=2 ‎ ‎∴AF= DF =1----------------------------------------8分 由(1)得△ABE≌△ADF ‎∴AE=DF=1‎ ‎∴EF=AF-AE=-----------------------------------------10分 ‎14．（2010山东聊城）如图，在等边△ABC中，点D是BC边的中点，以AD为边作等边△ADE．‎ ‎（1）求∠CAE的度数；‎ ‎（2）取AB边的中点F，连结CF、CE，试证明四边形AFCE是矩形．‎ 第22题图 ‎【答案】（1）在等边△ABC中，∵点D是BC边的中点，∴∠DAC＝30º，又∵等边△ADE，∴∠DAE＝60º，∴∠CAE＝30º ‎（2）在等边△ABC中，∵F是AB边的中点，D是BC边的中点，∴CF＝AD，∠CFA＝90º，又∵AD＝AE，∴AE＝CF，由（1）知∠CAE＝30º，∴∠EAF＝60º+30º＝90º，∴∠CFA＝∠EAF，∴CF∥AE，∵AE＝CF，∴四边形AFCE是平行四边形，又∵∠CFA＝90º，∴四边形AFCE是矩形．‎ ‎15．（2010湖南长沙）在正方形ABCD中，AC为对角线，E为AC上一点，连接EB、ED ‎（1）求证：△BEC≌△DEC；‎ ‎（2）延长BE交AD于F，当∠BED＝120°时，求的度数．‎ ‎【答案】解：（1）∵四边形ABCD是正方形，‎ ‎∴BC＝DC 又∵AC为对角线，E为AC上一点，‎ ‎∴∠BCE＝∠DCE＝45°．‎ ‎∵EC＝EC,‎ ‎∴△BEC≌△DEC(SAS)；‎ ‎（2）∵△BEC≌△DEC, ∠BED＝120°,‎ ‎∴∠BEC＝∠DEC＝60°．‎ ‎∵∠DAC＝45°，‎ ‎∴∠ADE＝15°‎ ‎∴∠EFD＝∠BED－∠ADE＝120°－15°＝105°‎ ‎16．（2010浙江金华(本题12分)如图，把含有30°角的三角板ABO置入平面直角坐标系中，A，B两点坐标分别为 ‎（3，0）和(0，3）.动点P从A点开始沿折线AO-OB-BA运动，点P在AO，OB，‎ BA上运动的 面四民﹒数学兴趣小组对捐款情况进行了抽样调查，速度分别为1，，2 (长度单位/秒)﹒一直尺的上边缘l从x轴的位置开 始以 (长度单位/秒)的速度向上平行移动（即移动过程中保持l∥x轴），且分别与 OB，‎ AB交于E，F两点﹒设动点P与动直线l同时出发，运动时间为t秒，当点P沿折线 AO-OB-BA运动一周时，直线l和动点P同时停止运动．‎ 请解答下列问题：‎ ‎（1）过A，B两点的直线解析式是▲；‎ ‎（2）当t﹦4时，点P的坐标为▲；当t ﹦▲，点P与点E重合；‎ ‎（3）①作点P关于直线EF的对称点P′. 在运动过程中，若形成的四边形PEP′F为 菱形，则t的值是多少？‎ ‎②当t﹦2时，是否存在着点Q，使得△FEQ ∽△BEP ?若存在,求出点Q的坐标；‎ B F A P E O x y ‎(第24题图)‎ 若不存在，请说明理由．‎ ‎【答案】‎ 解：（1）；（2）（0,），；‎ ‎（3）①当点在线段上时，过作⊥轴，为垂足（如图1）‎ B F A P E O x y G P′‎ P′‎ ‎(图1)‎ ‎∵,,∠∠90°‎ ‎∴△≌△，∴﹒‎ 又∵,∠60°,∴‎ 而，∴,‎ B F A P E O x y M P′‎ H ‎（图2)‎ 由得；‎ 当点P在线段上时，形成的是三角形，不存在菱形；‎ 当点P在线段上时，‎ 过P作⊥，⊥，、分别为垂足（如图2）‎ ‎∵,∴,∴‎ ‎∴，又∵‎ 在Rt△中，‎ 即，解得．‎ B F A P E O x Q′‎ B′‎ Q C C1‎ D1‎ ‎(图3)‎ y ‎②存在﹒理由如下：‎ ‎∵，∴,，‎ 将△绕点顺时针方向旋转90°，得到 ‎△（如图3）‎ ‎∵⊥，∴点在直线上，‎ C点坐标为（，－1）‎ 过作∥，交于点Q,‎ 则△∽△‎ 由，可得Q的坐标为（－，）‎ 根据对称性可得，Q关于直线EF的对称点（－，）也符合条件。‎ ‎17．（2010江苏泰州）如图，四边形ABCD是矩形，∠EDC=∠CAB，∠DEC=90°．‎ ‎(1)求证：AC∥DE；‎ ‎(2)过点B作BF⊥AC于点F，连结EF，试判断四边形BCEF的形状，并说明理由．‎ ‎【答案】⑴在矩形ABCD中，AC∥DE，∴∠DCA=∠CAB，∵∠EDC=∠CAB，‎ ‎∴∠DCA=∠EDC，∴AC∥DE；‎ ‎⑵四边形BCEF是平行四边形．‎ 理由：由∠DEC=90°，BF⊥AC，可得∠AFB=∠DEC=90°，‎ 又∠EDC=∠CAB，AB=CD，‎ ‎∴△DEC≌△AFB，∴DE=AF，由⑴得AC∥DE，‎ ‎∴四边形AFED是平行四边形，∴AD∥EF且AD=EF，‎ ‎∵在矩形ABCD中，AD∥BC且AD=BC，‎ ‎∴EF∥BC且EF=BC，‎ ‎∴四边形BCEF是平行四边形．‎ ‎18．（2010江苏无锡）‎ ‎（1）如图1，在正方形ABCD中，M是BC边（不含端点B、C）上任意一点，P是BC延长线上一点，N是∠DCP的平分线上一点．若∠AMN=90°，求证：AM=MN．‎ 下面给出一种证明的思路，你可以按这一思路证明，也可以选择另外的方法证明．‎ 证明：在边AB上截取AE=MC，连ME．正方形ABCD中，∠B=∠BCD=90°，AB=BC．‎ ‎∴∠NMC=180°—∠AMN—∠AMB=180°—∠B—∠AMB=∠MAB=∠MAE．‎ ‎（下面请你完成余下的证明过程）‎ 图1‎ 图2‎ ‎（2）若将（1）中的“正方形ABCD”改为“正三角形ABC”（如图2），N是∠ACP的平分线上一点，则当∠AMN=60°时，结论AM=MN是否还成立？请说明理由．‎ ‎（3）若将（1）中的“正方形ABCD”改为“正边形ABCD……X”，请你作出猜想：当∠AMN=°时，结论AM=MN仍然成立．（直接写出答案，不需要证明）‎ ‎【答案】解：（1）∵AE=MC，∴BE=BM， ∴∠BEM=∠EMB=45°， ∴∠AEM=135°， ‎ ‎∵CN平分∠DCP，∴∠PCN=45°，∴∠AEM=∠MCN=135°‎ ‎ 在△AEM和△MCN中：∵∴△AEM≌△MCN，∴AM=MN ‎ （2）仍然成立．‎ ‎ 在边AB上截取AE=MC，连接ME ‎∵△ABC是等边三角形，‎ ‎∴AB=BC，∠B=∠ACB=60°，‎ ‎∴∠ACP=120°．‎ ‎∵AE=MC，∴BE=BM ‎∴∠BEM=∠EMB=60°‎ ‎∴∠AEM=120°．‎ ‎∵CN平分∠ACP，∴∠PCN=60°，‎ ‎∴∠AEM=∠MCN=120°‎ ‎∵∠CMN=180°—∠AMN—∠AMB=180°—∠B—∠AMB=∠BAM ‎∴△AEM≌△MCN，∴AM=MN ‎ （3）‎ ‎19．（2010山东临沂）如图1，已知矩形，点是边的中点，且.‎ ‎(1)判断的形状，并说明理由；‎ ‎(2)保持图1中的固定不变，绕点旋转所在的直线到图2中的位置（当垂线段、在直线的同侧）.试探究线段、、长度之间有什么关系？并给予证明；‎ ‎（第25题图）‎ ‎（3）保持图2 中的固定不变，继续绕点旋转所在的直线到图3中的位置（当垂线段、在直线的异侧）.试探究线段、、长度之间有什么关系？并给予证明.‎ ‎【答案】解：（1）△ABC是等腰直角三角形。‎ 如图（1）在矩形ABED中，‎ 因为点C是边DE的中点，且AB=2AD,‎ 所以AD=DC=CE=EB,‎ ‎∠D=∠E=90°.‎ ‎∴Rt△ADC≌Rt△BEC.‎ ‎∴AC=BC, ∠1=∠2=45°.‎ ‎∴∠ACB=90°.‎ ‎∴△ABC是等腰直角三角形。‎ ‎（2）DE=AD+BE.‎ 如图（2），在Rt△ADC和Rt△BEC中，‎ ‎∵∠1=∠CAD=90°,∠1+∠2=90°.‎ ‎∴∠CAD=∠2.‎ 又∵AC=BC, ∠ADC=∠CEB=90°,‎ ‎∴Rt△ADC≌Rt△CEB.‎ ‎∴DC=BE,CE=AD.‎ ‎∴DC+CE= BE+AD,‎ 即DE=AD+BE.‎ ‎（3）DE=BE-AD.‎ 如图（3），在Rt△ADC和Rt△CEB中，∵∠1+∠CAD=90°,∠1+∠2=90°，‎ ‎∴∠CAD=∠2.‎ 又∵∠ADC=∠CBE=90°,AC=CB,∴Rt△ADC≌Rt△CBE.‎ ‎∴DC=BE,CE=AD.∴DC-CE=BE-AD, 即DE=BE-AD.‎ ‎20．（2010四川宜宾）‎ 已知：如图，在Rt△ABC中，∠C=90°，过点B作BD∥AC，且BD=2AC，连接AD．‎ ‎21题图 试判断△ABD的形状，并说明理由．‎ ‎【答案】过点A作AE垂直BD与点E，则四边形ACBE为矩形，所以CB=EA，AC=BE，且BD=2AC，所以BE=ED=AC，在Rt⊿ACB和Rt⊿AED中，‎ ED=AC，CB=EA，∠ACB=∠AED= 90°，所以Rt⊿ACB≌ Rt⊿AED（SAS）．‎ 所以AB=AD，所以三角形ABD为等腰三角形．‎ ‎21．（2010湖南衡阳）如图，在正方形ABCD中，点E、F分别在BC、CD上移动，但A到EF的距离AH始终保持与AB长相等，问在E、F移动过程中：‎ ‎（1）∠EAF的大小是否有变化？请说明理由．‎ ‎（2）△ECF的周长是否有变化？请说明理由．‎ ‎【答案】不变，理由是：在Rt△ABE和Rt△AHE中，AB=AH，AE=AE，所以Rt△ABE∽Rt△AHE，所以HE=BE，同理HF=DF.所以△ECF的周长=EF+CE+CF=BC+DC.可见△ECF的周长等于正方形边长的两倍.‎ ‎22．（2010 黄冈）（6分）如图，一个含45°的三角板HBE的两条直角边与正方形ABCD的两邻边重合，过E点作EF⊥AE交∠DCE的角平分线于F点，试探究线段AE与EF的数量关系，并说明理由。‎ ‎ 第18题图 ‎【答案】提示：由∠H＝∠FCE，AH＝CE，∠HAE＝∠FCE可证△HAE≌△CEF，从而得到 AE＝EF.‎ ‎23．（2010 山东莱芜）在平行四边形ABCD中，AC、BD交于点O，过点O作直线EF、GH，分别交平行四边形的四条边于E、G、F、H四点，连结EG、GF、FH、HE.‎ ‎（1）如图①，试判断四边形EGFH的形状，并说明理由；‎ ‎（2）如图②，当EF⊥GH时，四边形EGFH的形状是；‎ ‎（3）如图③，在（2）的条件下，若AC=BD，四边形EGFH的形状是；‎ ‎（4）如图④，在（3）的条件下，若AC⊥BD，试判断四边形EGFH的形状，并说明理由.‎ H G F E O D C B A 图①‎ H G F E O D C B A 图②‎ A B C D O E F G H 图③‎ A B C D O E F G H 图④‎ ‎（第23题图）‎ ‎【答案】解：（1）四边形EGFH是平行四边形． ‎ 证明：∵ABCD的对角线AC、BD交于点O．‎ ‎∴点O是 ABCD的对称中心．‎ ‎∴EO=FO，GO=HO．‎ ‎∴四边形EGFH是平行四边形． ‎ ‎（2）菱形． ‎ ‎（3）菱形． ‎ ‎（4）四边形EGFH是正方形． ‎ 证明：∵AC=BD，∴ABCD是矩形．又∵AC⊥BD， ∴ABCD是菱形．‎ ‎∴ABCD是正方形，∴∠BOC=90°，∠GBO=∠FCO=45°．OB=OC．‎ ‎∵EF⊥GH ，∴∠GOF=90°．∴∠BOG=∠COF．‎ ‎∴△BOG≌△COF．∴OG=OF，∴GH=EF． ‎ 由（1）知四边形EGFH是平行四边形，又∵EF⊥GH，EF=GH.‎ ‎∴四边形EGFH是正方形． ‎ ‎24．（2010福建宁德）如图，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM.‎ ‎⑴ 求证：△AMB≌△ENB；‎ ‎⑵①当M点在何处时，AM＋CM的值最小；‎ ‎②当M点在何处时，AM＋BM＋CM的值最小，并说明理由；‎ ‎⑶ 当AM＋BM＋CM的最小值为时，求正方形的边长.‎ E A D B C N M ‎【答案】解：⑴∵△ABE是等边三角形，‎ ‎∴BA＝BE，∠ABE＝60°.‎ ‎∵∠MBN＝60°，‎ ‎∴∠MBN－∠ABN＝∠ABE－∠ABN.‎ 即∠BMA＝∠NBE.‎ 又∵MB＝NB，‎ ‎∴△AMB≌△ENB（SAS）.………………5分 ‎⑵①当M点落在BD的中点时，AM＋CM的值最小.‎ F E A D B C N M ‎②如图，连接CE，当M点位于BD与CE的交点处时，‎ AM＋BM＋CM的值最小.‎ 理由如下：连接MN.由⑴知，△AMB≌△ENB，‎ ‎∴AM＝EN.‎ ‎∵∠MBN＝60°，MB＝NB，‎ ‎∴△BMN是等边三角形.‎ ‎∴BM＝MN.‎ ‎∴AM＋BM＋CM＝EN＋MN＋CM.‎ 根据“两点之间线段最短”，得EN＋MN＋CM＝EC最短 ‎∴当M点位于BD与CE的交点处时，AM＋BM＋CM的值最小，即等于EC的长.‎ ‎⑶过E点作EF⊥BC交CB的延长线于F，‎ ‎∴∠EBF＝90°－60°＝30°.‎ 设正方形的边长为x，则BF＝x，EF＝.‎ 在Rt△EFC中，‎ ‎∵EF2＋FC2＝EC2，‎ ‎∴（）2＋（x＋x）2＝.‎ 解得，x＝（舍去负值）.‎ ‎∴正方形的边长为.‎ ‎25．（2010浙江湖州）如图，已知在矩形ABCD中，AB＝2，BC＝3，P是线段AD边上的任意一点（不含端点A，D），连接PC，过点P作PE⊥PC交AB于E．‎‎（第25题）‎ ‎（1）在线段AD上是否存在不同于P的点Q，使得QC⊥QE？若存在，‎ 求线段AP与AQ之间的数量关系；若不存在，请说明理由；‎ ‎（2）当点P在AD上运动时，对应的点E也随之在AB上运动，求BE的取值范围．‎ ‎【答案】（1）存在，理由如下：假设存在这样的点Q，∵FE⊥PC，∴∠APE＋∠DPC＝90°，∵∠D＝90°，‎ ‎∴∠DPC＋∠DCP＝90°，∴△PAE∽△PDC，∴，∴，同理可得，∴，即，‎ ‎∴，∴，‎ ‎∴‎ ‎∵AP≠AQ，∴AP＋AQ＝3.∵AP≠AQ，∴AP≠，即P不能是AD的中点，∴当P是AD的中点时，满足条件的Q点不存在，故，当P不是AD的中点时，总存在这样的点Q满足条件，此时AP＋AQ＝3．‎ ‎（2）设AP＝x，BE＝y，则DP＝3－x，AE＝2－y，又PE⊥PC，∴△PAE∽△PDC，∴，即，∴，当时，y有最小值，y的最小值为，又E在AB上运动，且AB＝2，∴BE的取值范围是≤BE＜2．‎ ‎26．（2010江苏常州）如图，在△ABC中，AB=AC，D为BC中点，四边形ABDE是平行四边形。求证：四边形ADCE是矩形。‎ ‎【答案】‎ ‎27．（2010 四川成都）已知：在菱形中，是对角线上的一动点．‎ ‎（1）如图甲，为线段上一点，连接并延长交于点，当是的中点时，求证：；‎ ‎（2）如图乙，连结并延长，与交于点，与的延长线交于点．若，求和的长．‎ ‎【答案】（1）证明：∵ABCD为菱形，∴AD∥BC。‎ ‎∴∠OBP=∠ODQ ‎∵O是是的中点，‎ ‎∴OB=OD ‎ 在△BOP和△DOQ中，‎ ‎∵∠OBP=∠ODQ，OB=OD，∠BOP=∠DOQ ‎∴△BOP≌△DOQ（ASA）‎ ‎∴OP=OQ。‎ ‎（2）解：如图，过A作AT⊥BC，与CB的延长线交于T.‎ ‎∵ABCD是菱形，∠DCB=60°‎ ‎∴AB=AD=4，∠ABT=60°‎ ‎∴AT=ABsin60°=‎ TB=ABcos60°=2‎ ‎∵BS=10，∴TS=TB+BS=12，‎ ‎∴AS=。‎ ‎∵AD∥BS，∴△AOD∽△SOB。‎ ‎∴，‎ 则,∴‎ ‎∵AS=，∴。‎ 同理可得△ARD∽△SRC。‎ ‎∴,‎ 则,∴，‎ ‎∴。‎ ‎∴OR=OS-RS=。‎ ‎28．（2010湖南常德）如图5，已知四边形ABCD是菱形，DE⊥AB，DF⊥BC.求证:△ADE≌△CDF.‎ A B C D E F 图5‎ ‎【答案】证明：在△ADE和△CDF中,‎ ‎∵四边形ABCD是菱形,‎ ‎∴∠A=∠C，AD=CD. ‎ 又DE⊥AB，DF⊥BC,‎ ‎∴∠AED=∠CFD=900. ‎ ‎∴△ADE≌△CDF. ‎ ‎29．（2010湖南常德）如图10，若四边形ABCD、四边形GFED都是正方形，显然图中有AG=CE，AG⊥CE.‎ ‎（1）当正方形GFED绕D旋转到如图11的位置时，AG=CE 是否成立？若成立，请给出证明；若不成立，请说明理由.‎ ‎（2）当正方形GFED绕D旋转到如图12的位置时，延长CE交AG于H，交AD于M.‎ ‎①求证：AG⊥CH；‎ B A C D E F G H ‎ 图12‎ A B C D E F G 图11‎ ‎②当AD=4，DG=时，求CH的长.‎ A B C D E F G 图10‎ M ‎【答案】解：（1）成立．‎ 四边形、四边形是正方形，‎ ‎　　　　　　∴‎ ‎∠∠.‎ ‎∴∠90°-∠∠. ‎ ‎　　　　　　∴△△.‎ ‎∴. ‎ A B C D E F G 图11‎ B A C D E F G ‎1‎ ‎2‎ 图12‎ H P M ‎（2）①类似（1）可得△△，‎ ‎∴∠1＝∠2‎ ‎ 又∵∠＝∠. ‎ ‎∴∠∠＝.‎ 即 ‎②解法一: 过作于,‎ 由题意有,‎ ‎　　　　　　∴，则∠1＝. ‎ ‎　　　　　　而∠1＝∠2，∴∠2＝＝∠1＝.‎ ‎　　　　　　∴　，即. ‎ ‎　　　　　　在Rt中，＝＝,‎ 而∽,∴,即,‎ ‎∴.‎ 再连接，显然有,‎ ‎∴.‎ 所求的长为. ‎ B A C D E F G ‎1‎ ‎2‎ 图12‎ H P M 解法二：研究四边形ACDG的面积 过作于,‎ 由题意有,‎ ‎∴,. ‎ 而以CD为底边的三角形CDG的高=PD=1,‎ ‎,‎ ‎∴4×1+4×4=×CH+4 ×1.‎ ‎∴=. ‎ ‎30．（2010江苏扬州）如图，四边形ABCD是菱形，点G是BC延长线上一点，连接AG，分别交BD、CD于点E、F，连接CE．‎ ‎（1）求证：∠DAE＝∠DCE；‎ ‎（2）当AE＝2EF时，判断FG与EF有何等量关系？并证明你的结论？‎ A B C D E F G ‎【答案】（1）证明：∵四边形ABCD是菱形 ‎∴∠ADE=∠CDE，AD=CD ‎∵DE是公共边 ‎∴△ADE≌△CDE（SAS）‎ ‎∴∠DAE=∠DCE ‎(2)FG=3EF 解法一：∵四边形ABCD是菱形 ‎∴AD∥BC，∠DAE=∠G ‎∵∠DAE=∠DCE ‎∴∠DCE=∠G ‎∵∠CEF=∠GEC ‎∴△ECF∽△EGC ‎∴‎ ‎∵△ADE≌△CDE ‎∴EA=EC ‎∴‎ ‎∵AE=2EF ‎∴EG=2EC=4EF ‎∴FG=3EF 解法二：∵四边形ABCD是菱形 ‎∴AB∥CD ‎∴△ABE∽△FDE ‎∴‎ 同理△BEG∽△DEA ‎∴‎ ‎∴EG=2AE=4EF ‎∴FG=3EF ‎31. （2010北京）阅读下列材料：‎ 小贝遇到一个有趣的问题：在矩形ABCD中，AD＝8cm，AB＝6cm．现有一动点P按下列方式在矩形内运动：它从A点出发，沿着与AB边夹角为45°的方向作直线运动，每次碰到矩形的一边，就会改变运动方向，沿着与这条边夹角为45°的方向作直线运动，并且它一直按照这种方式不停地运动，即当点P碰到BC边，沿着与BC边夹角为45°的方向作直线运动，当点P碰到CD边，再沿着与CD边夹角为45°的方向作直线运动，…，如图1所示．问P点第一次与D点重合前与边相碰几次，P点第一次与D点重合时所经过的路径的总长是多少．‎ 小贝的思考是这样开始的：如图2，将矩形ABCD沿直线CD折叠，得到矩形A1B1CD．由轴对称的知识，发现P2P3＝P2E，P1A＝P1E．‎ 图1 图2‎ 请你参考小贝的思路解决下列问题：‎ ‎（1）P点第一次与D点重合前与边相碰______次；P点从A点出发到第一次与D点重合时所经过的路径的总长是________cm；‎ ‎（2）进一步探究：改变矩形ABCD中AD、AB的长，且满足AD＞AB．动点P从A点出发，按照阅读材料中动点的运动方式，并满足前后连续两次与边相碰的位置在矩形ABCD相邻的两边上．若P点第一次与B点重合前与边相碰7次，则AB∶AD的值为________．‎ ‎【答案】解：（1）5，24 ‎ （2）4∶5‎ 解题思路示意图：‎ ‎32.如图，△ABC是等腰直角三角形，∠A=90ｏ，点P、Q分别是AB、AC上的动点，且满足BP=AQ，D是BC的中点.‎ （１） 求证：△PDQ是等腰直角三角形；‎ （２） 当点P运动到什么位置时，四边形ＡPDQ是正方形，说明理由.‎ 解：（1）证明：连结AD ‎∵△ABC是等腰直角三角形，D是BC的中点 ‎　　　∴AD⊥BC，AD=BD=DC，∠DAQ=∠B 又∵BP=AQ ‎∴△BPD≌△AQD ‎∴PD=QD，∠ADQ=∠BDP ‎∵∠BDP+∠ADP=90ｏ ‎∴∠ADQ+∠ADP=∠PDQ=90ｏ ‎∴△PDQ为等腰直角三角形.‎ ‎（2）当P点运动到AB的中点时，四边形ＡPDQ是正方形.‎ ‎　　　由（１）知△ABD为等腰直角三角形.‎ 当P点运动到AB的中点时，DP⊥AB，即∠APD=90ｏ 又∵∠A=90ｏ，∠PDQ=90ｏ ‎∴四边形ＡPDQ为矩形 又∵DP=AP=AB ‎∴四边形ＡPDQ是正方形.‎ ‎33. （2010云南红河哈尼族彝族自治州）如图6，在正方形ABCD中，G是BC上的任意一点，（G与B、C两点不重合），E、F是AG上的两点（E、F与A、G两点不重合），若AF=BF+EF，∠1=∠2，请判断线段DE与BF有怎样的位置关系，并证明你的结论.‎ ‎【答案】解：根据题目条件可判断DE//BF.‎ 证明如下：‎ ‎∵四边形ABCD是正方形，‎ ‎∴AB=AD，∠BAF+∠2=90°.‎ ‎∵AF=AE+EF，又AF=BF+EF ‎∴AE=BF ‎∵∠1=∠2，∴△ABF≌△DAE（SAS）.‎ ‎∴∠AFB=∠DEA，∠BAF=∠ADE.‎ ‎∴∠ADE+∠2=90°，‎ ‎∴∠AED=∠BFA=90°.‎ ‎∴DE//BF. ‎ ‎34. （2010湖北随州）如图，一个含45°的三角板HBE的两条直角边与正方形ABCD的两邻边重合，过E点作EF⊥AE交∠‎ DCE的角平分线于F点，试探究线段AE与EF的数量关系，并说明理由。‎ ‎ 第18题图 ‎【答案】提示：由∠H＝∠FCE，AH＝CE，∠HAE＝∠FCE可证△HAE≌△CEF，从而得到AE＝EF.‎ ‎35. （2010江苏徐州）如图，在△ABC中，D是BC边的中点，E、F分别在AD及其延长线上， CE∥BF，连接BE、CF．‎ ‎ (1)求证：△BDF≌△CDE；‎ ‎ (2)若AB=AC，求证：四边形BFCE是菱形．‎ ‎【答案】‎ ‎36. （2010江苏徐州）如图①，将边长为4cm的正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上)，使点B落在AD边上的点 M处，点C落在点N处，MN与CD交于点P， 连接EP．‎ ‎ (1)如图②，若M为AD边的中点，‎ ‎ ①,△AEM的周长=_____cm；‎ ‎ ②求证：EP=AE+DP；‎ ‎ (2)随着落点M在AD边上取遍所有的位置(点M不与A、D重合)，△PDM的周长是否发生变化?请说明理由．‎ ‎【答案】‎ ‎37. （2010陕西西安）如图，A、B、C三点在同一条直线上，AB=2BC。分别以 AB、BC为边作正方形ABEF和正方形BCMN，连接FN，‎ EC。‎ ‎ 求证：FN=EC。‎ ‎【答案】证明：FN=EC。‎ 证明：在正方形ABEF和正方形BCMN中，‎ AB=BE=EF，BC=BN，∠FEN=∠EBC=90°‎ ‎∵AB=2BC ‎∴EN=BC ‎ ‎∴△FEN≌△EBC ‎ ‎∴FN=EC。 ‎ ‎38. （2010广东东莞）如图（1），（2）所示，矩形ABCD的边长AB＝6，BC＝4，点F在DC 上，DF＝2．动点M、N分别从点D、B同时出发，沿射线DA、线段BA向点A的方向运动（点M可运动到DA的延长线上），当动点N运动到点A时，M、N两点同时停止运动．连接FM、MN、FN，当F、N、M不在同一直线时，可得△FMN，过△FMN三边的中点作△PQW．设动点M、N的速度都是1个单位／秒，M、N运动的时间为x秒．试解答下列问题：‎ ‎⑴说明△FMN ∽△QWP；‎ ‎⑵设0≤≤4（即M从D到A运动的时间段）．试问为何值时，△PQW为直角三角形？当在何范围时，△PQW不为直角三角形？‎ ‎⑶问当为何值时，线段MN最短？求此时MN的值．‎ ‎【答案】⑴∵P、Q、W分别为△FMN三边的中点 ‎∴PQ∥FN，PW∥MN ‎∴∠MNF＝∠PQM＝∠QPW 同理：∠NFM＝∠PQW ‎∴△FMN ∽△QWP ‎⑵‎ 由⑴得△FMN ∽△QWP，所以△FMN为直角三角形时，△QWP也为直角三角形．如图，过点N作NECD于E，根据题意，得DM＝BM＝，∴AM＝4－，AN＝DE＝6－‎ ‎∵DF＝2，∴EF＝4－‎ ‎∴MF2＝22＋x2＝x2＋4，MN2＝（4－x）2＋（6－x）2＝2x2－20x＋52，NF2＝（4－x）2＋42＝x2－8x＋32,‎ ① 如果∠MNF＝90°，则有2x2－20x＋52＋x2－8x＋32＝x2＋4，解得x1＝4，x2＝10（舍去）；‎ ‎②如果∠NMF＝90°，则有2x2－20x＋52＋x2＋4＝x2－8x＋32，化简，得：x2－6x ‎＋12＝0，△＝－12＜0，方程无实数根；‎ ‎③如果∠MFN＝90°，则有2x2－20x＋52＝x2＋4＋x2－8x＋32，解得x＝．‎ ‎∴当为4或时，△PQW为直角三角形，当0≤＜或＜＜4时，△PQW不为直角三角形 ‎⑶∵点M在射线DA上，点N在线段AB上，且AB⊥AD，∴当M点运动到与A点重合时，NM⊥AD，根据垂线段最短原理，此时线段MN最短，DM＝4，则BN＝4．‎ ‎∴当＝4时，线段MN最短，MN＝２．‎ ‎39. （2010 福建三明）正方形ABCD中，点O是对角线AC的中点，P为对角线AC 上一动点，过点P作PF⊥DC于点F，如图1，当点P与点O 重合时，显然有DF=CF。‎ ‎ （1）如图2，若点P在线段AO上（不与A、O重合0，PE⊥PB且PE交CD点E。‎ ‎①求证：DF=EF；②写出线段PC、PA、CE之间的一个等量关系式，并证明 你的结论；‎ ‎ （2）若点P在线段CA的延长线上，PE⊥PB且PE交直线CD 于点E。请完成图3并判断（1）中的结论①、②是否成立？‎ 若不成立，写出相应的结论（所写结论均不必证明）‎ ‎【答案】（1）证明：延长FP交AB于点Q，证明≌即可得出…………4分 ‎ （2）解：PC-PA=‎ 理由如下……8分 ‎ （3）正确完成图3得1分，结论①仍成立，②不成立 …………11分 此时②中三条线段的数量关系是…………‎ ‎40．（2010广东汕头）如图（1），（2）所示，矩形ABCD的边长AB＝6，BC＝4，点F在DC上，DF＝2．动点M、N分别从点D、B同时出发，沿射线DA、线段BA向点A的方向运动（点M可运动到DA的延长线上），当动点N运动到点A时，M、N两点同时停止运动．连接FM、FN，当F、N、M不在同一直线时，可得△FMN，过△FMN三边的中点作△PWQ．设动点M、N的速度都是1个单位/秒，M、N运动的时间为x秒．试解答下列问题：‎ ‎（1）说明△FMN∽△QWP；‎ ‎（2）设0≤x≤4（即M从D到A运动的时间段）．试问x为何值时，△PWQ为直角三角形？当x在何范围时，△PQW不为直角三角形？‎ ‎（3）问当x为何值时，线段MN最短？求此时MN的值．‎ 第22题图（2）‎ A B C D F 第22题图（1）‎ A B M C F D N W P Q M N W P Q ‎【答案】解：（1）∵P、Q、W分别是△FMN的中点 ‎∴PQ∥NF，QW∥MF，PW∥MN ‎∴四边形PQWF、MQWP、PQNW都是平行四边形，‎ ‎∴∠F＝∠PQW，∠M＝∠PWQ ‎∴△FMN∽△QWP．‎ ‎ （2）∵△FMN∽△QWP，△PWQ为直角三角形 ‎∴△FMN也是直角三角形 ‎∵MF2＝4＋x2，MN2＝（4－x）2＋（6－x）2，MF2＝42＋（4－x）2，‎ ‎∴①若MF为斜边，则4＋x2＝（4－x）2＋（6－x）2＋42＋（4－x）2‎ 解得，因0≤x≤4得，；‎ ‎②若MN为斜边，则（4－x）2＋（6－x）2＝4＋x2＋42＋（4－x）2‎ 解得；‎ ‎③若NF为斜边，则42＋（4－x）2＝（4－x）2＋（6－x）2＋4＋x2‎ 此方程无实数解．‎ 综上，当或时，△PWQ为直角三角形；而当 或或时，△PQW不为直角三角形．‎ ‎（3）①当0≤x≤4时，易知当x＝4时，MN有最小值为2．‎ ‎②4＜x≤6时，MN2＝（x－4）2＋（6－x）2，故 ，此时，当 x＝5时，MN有最小值为．‎ 综上，x＝5时，MN有最小值为．‎ ‎41．（2010 山东淄博）已知：如图，E为正方形ABCD的边BC延长线上的点，F是CD边上一点，且CE＝CF，连接DE，BF．求证：DE＝BF．‎ F E D C B A ‎(第19题)‎ ‎【答案】证明：∵四边形ABCD是正方形，∴BC=DC，∠BCD=90º ‎∵E为BC延长线上的点，∴∠DCE=90º，∴∠BCD=∠DCE．‎ ‎∵CE＝CF，∴△BCF≌△DCE，∴DE＝BF．‎ ‎42．（2010 天津）在平面直角坐标系中，矩形的顶点O在坐标原点，顶点A、B 分别在轴、‎ 轴的正半轴上，，，D为边OB的中点.‎ 温馨提示：如图，可以作点D关于轴的对称点，连接与轴交于点E，此时△的周长是最小的.这样，你只需求出的长，就可以确定点的坐标了.‎ ‎（Ⅰ）若为边上的一个动点，当△的周长最小时，求点的坐标；‎ 第（25）题 y B O D C A x E y B O D C A x ‎（Ⅱ）若、为边上的两个动点，且，当四边形的周长最小时，求点、的坐标.‎ ‎【答案】解：（Ⅰ）如图，作点D关于轴的对称点，连接与轴交于点E，连接.‎ 若在边上任取点（与点E不重合），连接、、.‎ y B O D C A x E 由，‎ 可知△的周长最小.‎ ‎∵在矩形中，，，为的中点，‎ ‎∴，，.‎ ‎∵OE∥BC，‎ ‎∴Rt△∽Rt△，有.‎ ‎∴.‎ ‎∴点的坐标为（1，0）. ．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．6分 y B O D C A x E G F ‎（Ⅱ）如图，作点关于轴的对称点，在边上截取，连接与轴交于点，在上截取.‎ ‎∵GC∥EF，，‎ ‎∴四边形为平行四边形，有.‎ 又 、的长为定值，‎ ‎∴ 此时得到的点、使四边形的周长最小. ‎ ‎∵OE∥BC，‎ ‎∴Rt△∽Rt△, 有 .‎ ‎∴.‎ ‎∴.‎ ‎∴点的坐标为（，0），点的坐标为（，0）. ．．．．．．．．．．．．．．．10分 ‎43．（2010 湖南湘潭）Rt△ABC与Rt△FED是两块全等的含30o、60o角的三角板，按如图（一）所示拼在一起，CB与DE重合．‎ ‎（1）求证：四边形ABFC为平行四边形；‎ ‎（2）取BC中点O，将△ABC绕点O顺时钟方向旋转到如图（二）中△‎ 位置，直线与AB、CF分别相交于P、Q两点，猜想OQ、OP长度的大小关系，并证明你的猜想．‎ ‎ (3)在(2)的条件下,指出当旋转角至少为多少度时,四边形PCQB为菱形(不要求证明).‎ ‎23题图 ‎【答案】证：（1）……………………1分 ‎∴AB=CF，AC=BF……………………2分 ‎∴四边形ABCF为平行四边形 ……………………3分 ‎ （用其它判定方法也可）‎ ‎（2）OP=OQ……………………4分 理由如下：‎ ‎……………………6分 ‎∴OP=OQ ……………………7分 ‎(用平行四边形对称性证明也可) ‎ ‎ (3)90o……………………8分 ‎44．（2010广西桂林）求证：矩形的对角线相等．‎ ‎【答案】已知：四边形ABCD是矩形, AC与BD是对角线 ……………2分 求证：AC=BD………………………………………3分 证明：∵四边形ABCD是矩形 ‎∴AB=DC,∠ABC=∠DCB=90°…………4分 又∵BC=CB…………………………5分 ‎∴△ABC≌△DCB…………6分 ‎∴AC=BD……………………7分 所以矩形的对角线相等. …………8分 ‎45．（2010 四川自贡）如图，在□ABCD中，BE⊥AD于点E，BF⊥CD于点F，AC与BE、BF分别交于点G，H。‎ ‎（1）求证：△BAE∽△BCF ‎（2）若BG＝BH，求证四边形ABCD是菱形 ‎【答案】‎ ‎46．（2010宁夏回族自治区）已知：正方形ABCD中，E、F分别是边CD、DA上的点，且CE=DF，AE与BF交于点M．‎ ‎（1）求证：△ABF≌△DAE；‎ ‎（2）找出图中与△ABM相似的所有三角形（不添加任何辅助线）．‎ ‎【答案】(1)证明：在正方形ABCD中：‎ AB=AD=CD, 且∠BAD=∠ADC=‎ ‎∵CE=DF ‎∴AD-DF=CD-CE 即：AF=DE 在△ABF与△DAE中 ‎∴△ABF≌△DAE（SAS）‎ （2） 与△ABM相似的三角形有：△FAM; △FBA; △EAD ‎47．（2010宁夏回族自治区）在△ABC中，∠BAC=45°，AD⊥BC于D，将△ABD沿AB所在的直线折叠，使点D落在点E处；将△ACD沿AC所在的直线折叠，使点D落在点F处，分别延长EB、FC使其交于点M．‎ ‎(1)判断四边形AEMF的形状，并给予证明．‎ ‎(2)若BD=1，CD=2，试求四边形AEMF的面积．‎ ‎【答案】解：（1）∵ADBC ‎△AEB是由△ADB折叠所得 ‎∴∠1=∠3，∠E=∠ADB=，BE=BD, AE=AD 又∵△AFC是由△ADC折叠所得 ‎∴∠2=∠4，∠F=∠ADC=，FC=CD，AF=AD ‎∴AE=AF---------------------------------------------2分 ‎ 又∵∠1+∠2=， ‎ ‎∴∠3+∠4=‎ ‎∴∠EAF=--------------------------------------3分 ‎∴四边形AEMF是正方形。---------------------5分 ‎（2）方法一：设正方形AEMF的边长为x 根据题意知：BE=BD, CF=CD ‎∴BM=x－1; CM=x－2-------------------------------------------------------------------7分 在Rt△BMC中,由勾股定理得：‎ ‎∴‎ 解之得： (舍去)‎ ‎∴------------------------------------------10分 方法二：设：AD=x ‎∴=‎ ‎∴-----------------------------------------------------------7分 ‎∵‎ 且 ‎∴ 即 解之得： (舍去)‎ ‎∴---------------------------------------------10分 ‎48．（2010 广西钦州市）如图，梯形ABCD中，AB∥CD，AC平分∠BAD，‎ CE∥AD交AB于点E．求证：四边形AECD是菱形．‎ ‎【答案】证明：‎ ‎∵AB∥CD，CE∥AD， ‎ ‎∴四边形AECD是平行四边形.………3分 ‎ ‎∵AC平分∠BAD，‎ ‎∴∠BAC＝∠DAC.…………4分 ‎ 又∵AB∥CD，‎ ‎∴∠ACD＝∠BAC＝∠DAC.…………5分 ‎∴AD＝DC.…………6分 ‎∴四边形AECD是菱形.…………8分 ‎49．（2010 广西钦州市）如图，将OA= 6，AB = 4的矩形OABC放置在平面直角坐标系中，动点M、N以每秒１个单位的速度分别从点A、C同时出发，其中点M沿AO向终点O运动，点N沿CB向终点B运动，当两个动点运动了t秒时，过点N作NP⊥BC，交OB于点P，连接MP．‎ ‎ （1）点B的坐标为▲；用含t的式子表示点P的坐标为▲；(3分)‎ ‎（2）记△OMP的面积为S，求S与t的函数关系式（0 < t < 6）；并求t为何值时，S有最大值？(4分)‎ ‎（3）试探究：当S有最大值时，在y轴上是否存在点T，使直线MT把△ONC分割成三角形和四边形两部分，且三角形的面积是△ONC面积的？若存在，求出点T的坐标；若不存在，请说明理由．(3分)‎ ‎（备用图）‎ ‎【答案】解：（1）（6，4）；（）.（其中写对B点得1分） 3分 ‎（2）∵S△OMP =×OM×， 4分 ‎∴S =×（6 -t）×=+2t．‎ ‎ ＝（0 < t <6）． 6分 ‎∴当时，S有最大值． 7分 ‎ （3）存在．‎ ‎ 由（2）得：当S有最大值时，点M、N的坐标分别为：M（3，0），N（3，4），‎ 则直线ON的函数关系式为：．‎ ‎（备用图）‎ R2‎ T1‎ T2‎ R1‎ D2‎ D1‎ ‎ 设点T的坐标为（0，b），则直线MT的函数关系式为：，‎ 解方程组得 ‎∴直线ON与MT的交点R的坐标为．‎ ‎∵S△OCN ＝×4×3＝6，∴S△ORT ＝ S△OCN ＝2． 8分 ‎① 当点T在点O、C之间时，分割出的三角形是△OR1T1，如图，作R1D1⊥y轴，D1‎ 为垂足，则S△OR1T1＝••••RD1•OT ＝••b＝2.‎ ‎∴， b =.‎ ‎∴b1 ＝，b2 ＝（不合题意，舍去）‎ 此时点T1的坐标为（0，）. 9分 ‎② 当点T在OC的延长线上时，分割出的三角形是△R2NE，如图，设MT交CN于点E，由①得点E的横坐标为，作R2D2⊥CN交CN于点D2，则 S△R2NE＝•EN•R2D2=••＝2.‎ ‎∴，b=.‎ ‎∴b1＝，b2＝（不合题意，舍去）．‎ ‎∴此时点T2的坐标为（0，）．‎ 综上所述，在y轴上存在点T1（0，），T2（0，）符合条件．‎ ‎50．（2010吉林长春）（1）在图①中。以线段m为一边画菱形，要求菱形的顶点均在格点上。（画一个即可）（3分）‎ ‎（2）在图②中，平移a、b、c中的两条线段，使它们与线段n构成以n为一边的等腰直角三角形。（画一个即可）（3分）‎ ‎【答案】‎ ‎51．（2010吉林长春）如图,四边形ABCD与四边形DEFG都是矩形,顶点F在BA的延长线上,边DG与AF交于点H,AD=4,DH=5,EF=6,求FG的长.‎ ‎【答案】‎ ‎52．（2010新疆乌鲁木齐）如图5，在平行四边形ABCD中，BE平分∠ABC交 AD于点E，DF平分∠ADC交BC于点DF。‎ ‎ 求证：（1）△ABE≌△CDF ‎ （2）若BD⊥EF，则判断四边形EBFD是什么特殊 四边形，请证明你的结论。‎ ‎【答案】证明：（1）四边形ABCD是平行四边形 BE平分，DF平分…………2分 ‎（ASA） …………4分 ‎ （2）由，得AE=CF …………5分 ‎ 在平行四边形ABCD中，AD//BC，AD=BC 四边形EBFD是平行四边形 …………6分 ‎ 若，则四边形EBFD是菱形 …………8分 ‎53．（2010新疆乌鲁木齐）如图9，边长为5的正方形OABC的顶点O在坐标原点处，点A、C分别在x轴、y轴的正半轴上，点E是OA边上的点（不与点A重合），EF⊥CE，且与正方形外角平分线AG交于点P。‎ ‎ （1）当点E坐标为（3，0）时，试证明CE=EP；‎ ‎ （2）如果将上述条件“点E坐标为（3，0）”改为“点E坐标 为”，结论CE=EP是否仍然成立，请说明理由；‎ ‎ （3）在y轴上是否存在点M，使得四边形BMEP是平行四边 形？若存在，用t表示点M的坐标；若不存在，说明理由。‎ ‎【答案】解：（1）过点P作轴，垂足为H ‎∴△COE∽△EHP ‎………………2分 由题意知：CO=5 OE=3 EH=EA+AH=2+HP ‎………………3分 故CE=EP ………………5分 ‎ （2）CE=EP仍成立。‎ 同理△COE∽△EHP ………………6分 由题意知：CO=5 OE=t ‎ ‎…………8分 ‎ （3）y轴上存在点M，使得四边形BMEP是平行四边形 …………9分 过点B作BM//EP交y轴于点M 在△BCM和△COE中 ‎∴△BCM≌△COE ∴BM=CE 而CE=EP ∴BM=EP 由于BM//EP ∴四边形BMEP是平行四边形 …………11分 由△BCM≌△COE可得CM=OE=t ∴OM=CO—CM=5—t 故点M的坐标为………………12分 ‎54．（2010年山西）如图1，已知正方形ABCD是边CD的正方形DEFG的边DE上，连接AE，GC。‎ ‎ （1）试猜想AE与GC有怎样的位置关系，并证明你的结论。‎ ‎ （2）将正方形DEFG绕点D按顺时针方向旋转，使点E落在BC边上，如图2，连接AE和GC，你认为（1）中的结论是否还成立？若成立，给出证明：若不成立，请说明理由。‎ ‎【答案】（1）答：…………（1分）‎ ‎ 证明：延长GC交AE于点H ‎ 在正方形ABCD与正方形DEFG中，‎ ‎…………（3分）‎ ‎…………（5分）‎ ‎ （2）答：成立…………（6分）‎ ‎ 证明：延长AE和GC相交于点H。‎ ‎ 在正方形ABCD和正方形DEFG中，‎ ‎…………（8分）‎ ‎ 又 ‎，‎ ‎…………（10分）‎ ‎55．（2010广东茂名）如图，已知OA⊥OB，OA＝4，OB＝3，以AB为边作矩形ABCD，使AD＝，过点D作DE垂直OA的延长线交于点E．‎ ‎（1）证明：△OAB∽△EDA； （3分）‎ ‎（2）当为何值时，△OAB与△EDA全等？请说明理由；并求出此时点C到OE的距离． ‎ ‎(第22题图)‎ ‎(第22题备用图)‎ ‎【答案】（1）证明：如图示，‎ ‎∵OA⊥OB ，∴∠1与∠2互余，‎ 又∵四边形ABCD是矩形，∴∠BAD＝90o，‎ ‎∴∠2与∠3互余，∴∠1＝∠3，·········1分 ‎∵OA⊥OB，DE⊥OA，∴∠BOA＝∠DEA＝90o··2分 ‎∴△OAB∽△EDA．···························3分 ‎(2) 解：在Rt△OAB中，AB＝，········· 4分 由（1）可知∠1＝∠3，∠BOA＝∠DEA＝90o，‎ ‎∴当＝AD=AB=5时，△OAB与△EDA全等．···5分 当＝AD=AB=5时，可知矩形ABCD为正方形，‎ ‎∴BC＝AB，如图，过点C作CH⊥OE交OE于点H，‎ 则CH就是点C到OE的距离，过点B作BF⊥CH交CH于点F，‎ 则∠4与∠5互余，∠1与∠5互余，∴∠1＝∠4，·························6分 又∵∠BFC＝∠BOA，BC＝AB，∴△OAB≌△FCB（AAS），···············7分 ‎∴CF＝OA＝4，BO＝BF，∴四边形OHFB为正方形，‎ ‎∴HF＝OB＝3，∴点C到OE的距离CH＝CF+HF＝4+3＝7．················8分 ‎56．（2010辽宁大连）如图15，在△ABC中，AB=AC=5，BC=6，动点P从点A出发沿AB向点B移动，（点P与点A、B不重合），作PD//BC交AC于点D，在DC上取点E，以DE、DP为邻边作平行四边形PFED，使点F到PD的距离，连接BF，设 ‎（1）△ABC的面积等于 ‎（2）设△PBF的面积为，求与的函数关系，并求的最大值；‎ ‎（3）当BP=BF时，求的值 F H P A C B E D 图15‎ ‎【答案】‎ ‎57．（2010贵州遵义）如图（1），在⊿ABC和⊿EDC中，AC=CE=CB=CD，∠ACB=∠ECD=90°，AB与CE交于F，ED与AB、BC分别交于M、H.‎ ‎(1)求证：CF=CH；‎ ‎(2)如图（2），⊿ABC不动，将⊿EDC绕点C旋转到∠BCE=45° 时，试判断四边形ACDM是什么四边形？并证明你的结论。‎ ‎【答案】解：（1）（5分）证明：△ ACB和△ECD中 ‎∵∠ACB=∠ECD=90°‎ ‎∴∠1+∠ECB=∠2+∠ECB ‎∴∠1=∠2‎ 又∵AC=CE=CB=CD ‎∴∠A=∠D=45°‎ ‎∴△ACF≌△DCH ‎∴CF=CH ‎（2）（5分）答：四边形ACDM是菱形 证法一：∵∠ACB=∠ECD=90°，∠BCE=45°，‎ ‎∴∠1=45°，∠2=45°‎ 又∵∠E=∠B=45°，∴∠1=∠E，∠2=∠B ‎∴AC//MD，CD//AM 又∵AC=CD ‎∴ACDM是菱形 证法二：∵∠ACB=∠ECD=90°，∠BCE=45°，‎ ‎∴∠1=45°，∠2=45°‎ ‎∴∠ACD=∠1+∠BCE+∠2=135°‎ 又∵∠A=45°，∠D=45°‎ ‎∴∠A+∠ACD=180°，∠D+∠ACD=180°‎ ‎∴AC//MD，CD//AM 又∵AC=CD ‎∴ACDM是菱形 ‎58．（2010辽宁沈阳）如图，菱形ABCD的对角线AC与BD相交于点O，点E、F分别为边AB、AD的中点，连接EF、OE、OF．求证：四边形AEOF是菱形．‎ ‎【答案】证明：‎ ‎∵点E、F分别为AB、AD的中点 ‎∴AE=AB，AF=AD 又∵四边形ABCD是菱形 ‎∴AB=AD，‎ ‎∴AE=AF，………………………4分 又∵菱形ABCD的对角线AC与BD相交于点O ‎∴O为BD的中点，‎ ‎∴OE、OF是⊿ABD的中位线………………………6分 ‎∴OE∥AD，OF∥AB ‎∴四边形AEOF是平行四边形………………………8分 ‎∵AE=AF 四边形AEOF是菱形。………………………10分 ‎59．（2010辽宁沈阳）如图1，在△ABC中，点P为BC边中点，直线a绕顶点A旋转，若点B、P在直线a的异侧，BM⊥直线a于点M，CN⊥直线a于点N，连接PM、PN。‎ ‎（1）延长MP交CN于点E（如图2）。①求证：△BPM≌△CPE；②PM=PN；‎ ‎（2）若直线a绕点A旋转到图3的位置时，点B、P在直线a的同侧，其它条件不变，此时PM=PN成立吗？若成立，请给予证明，若不成立，请说明理由；‎ ‎（3）若直线a绕点A旋转到与BC边平行的位置时，其它条件不变。请直接判断四边形MBCN的形状及此时PM=PN还成立吗？不必说明理由.‎ ‎【答案】（1）证明：①如图2‎ ‎∵BM⊥直线a于点M，CN⊥直线a于点N ‎∴∠BMN=∠CNM=90°‎ ‎∴BM∥CN ‎∴∠MBP=∠ECP 又∵P为BC边中点 ‎∴BP=CP 又∵∠BPM=∠CPE ‎∴△BPM≌△CPE………………………………3分 ②∵△BPM≌△CPE ‎∴PM=PE ‎∴PM=ME ‎∴在Rt△MNE中，PN=ME ‎∴PM=PN……………………………………5分 ‎（2）成立。如图3…………………………………6分 证明：延长MP与NC的延长线相交于点E ‎∵BM⊥直线a于点M，CN⊥直线a于点N ‎∴∠BMN=∠CNM=90°‎ ‎∴∠BMN+∠CNM=180°‎ ‎∴BM∥CN ‎∴∠MBP=∠ECP…………………………………7分 又∵∠BPM=∠CPE ‎∴△BPM≌△CPE ‎∴PM=PE ‎∴PM=ME 则在直角三角形中，PM=ME ‎∴PM=PN……………………………………10分 ‎(3)四边形MBCN是矩形……………………………………11分 PM=PN成立……………………………………12分 ‎60．（2010福建南平）如图1，在△ABC中，AB=BC，P为AB边上一点，连接CP，以PA、PC为邻边作□APCD，AC与PD相交于点E，已知∠ABC=∠AEP=α（0°<α<90°）.‎ ‎（1）求证：∠EAP=∠EPA；‎ ‎（2）□APCD是否为矩形？请说明理由；‎ ‎（3）如图2，F为BC中点，连接FP，将∠AEP绕点E顺时针旋转适当的角度，得到∠MEN（点M、N分别是∠MEN的两边与BA、FP延长线的交点）.猜想线段EM与EN之间的数量关系，并证明你的结论.‎ 图1‎ A B D C E P 图2‎ A B D C E P M N F ‎【答案】(1)证明：在ΔABC和ΔAEP中 ‎∵∠ABC=∠AEP，∠BAC=∠EAP ‎∴∠ACB=∠APE 在ΔABC中，AB=BC ‎∴∠ACB=∠BAC ‎∴∠EPA=∠EAP (2) 答：□ APCD是矩形 ‎∵四边形APCD是平行四边形 ‎∴ AC=2EA, PD=2EP ‎∵由（1）知∠EPA=∠EAP ‎∴ EA=EP 则 AC=PD ‎∴□APCD是矩形 (3) 答： EM=EN ‎∵EA=EP ∴∠EPA=90°－α ‎∴∠EAM=180°-∠EPA=180°-(90°- α)=90°+α 由（2）知∠CPB=90°,F是BC的中点，∴ FP=FB ‎∴∠FPB=∠ABC=α ‎∴∠EPN=∠EPA+∠APN=∠EPA+∠FPB=90°- α+α=90°+α ‎∴∠EAM=∠EPN ‎∵∠AEP绕点E顺时针旋转适当的角度，得到∠MEN ‎ ‎∴∠AEP=∠MEN ‎ ‎∴∠AEP- ∠AEN=∠MEN-∠AEN 即∠MEA=∠NEP ‎∴ΔEAM≌ΔEPN ∴ EM=EN ‎61．（2010天门、潜江、仙桃）正方形ABCD中，点O是对角线DB的中点，点P是DB所在直线上的一个动点，PE⊥BC于E，PF⊥DC于F.‎ ‎ (1)当点P与点O重合时(如图①)，猜测AP与EF的数量及位置关系，并证明你的结论；‎ ‎ (2)当点P在线段DB上 (不与点D、O、B重合)时(如图②)，探究(1)中的结论是否成立？若成立，写出证明过程；若不成立，请说明理由；‎ ‎ (3)当点P在DB的长延长线上时，请将图③补充完整，并判断(1)中的结论是否成立？若成立，直接写出结论；若不成立，请写出相应的结论.‎ ‎【答案】（1）AP=EF，理由是：连接PC，易知△ABP≌△CBP，所以AP=PC，因为四边形PE=CF是正方形，所以PC=EF，所以AP=EF.‎ ‎（2）AP=EF，理由是：连接PC，易知△ABP≌△CBP，所以AP=PC，因为四边形PE=CF是矩形，所以PC=EF，所以AP=EF.‎ ‎（3）AP=EF，图形如图.‎ ‎62．（2010年福建省泉州）如图, 正方形中, 是上一点, 在的延长线上,且。‎ ‎ (1)求证:≌；‎ ‎(2)问：将顺时针旋转多少度后与重合，旋转中心是什么？ ‎ ‎【答案】（1）证明：在正方形ABCD中 ‎，…………（1分）‎ ‎，………（3分）‎ 又……………………………（4分）‎ ‎∴≌…………………………（5分）‎ ‎（2）将顺时针旋转 90 后与重合，…………………………………（7分）‎ 旋转中心是点 A ．…………………………………（9分）‎ ‎63．（2010广东肇庆）如图4，四边形ABCD是平行四边形，AC、BD交于点O，∠1=∠2.‎ （1） 求证：四边形ABCD是矩形；‎ （2） 若∠BOC=120ｏ，AB=4 cm,求四边形ABCD的面积.‎ ‎【答案】（1）证明：∵四边形ABCD是平行加边形，AC、BD交于点O ‎∴OA=OC，OB=OD ‎ 又∵∠1=∠2‎ ‎∴OB=OC ‎∴OA=OB=OC=OD ‎∴AC=BD ‎∴四边形ABCD是矩形 ‎ （2）∵四边形ABCD是矩形，∠BOC=120ｏ，AB=4‎ ‎∴∠1=∠2=30ｏ，BC=4‎ ‎∴S四边形ABCD=ABBC＝16cm２‎ ‎64．（2010四川广安）已知：如右图，在矩形ABCD中，BE=CF，求证：AF=DE．‎ ‎【答案】在矩形ABCD中，AB=AC，∠B=∠C=90°，又∵BE=CF，∴BE+EF=CF+EF，即BF=CE∴△ABF≌△DCE，∴AF=DE。‎ ‎65．（2010吉林）正方形ABCD与正方形CEFG的位置如图所示，点G在线段CD或CD的延长线上，分别连接BD、BF、FD，得到△BFD。‎ ‎（1）在图①~图③中，若正方形CEFG的国长分别为1、3、4，且正方形ABCD的边长均为3，请通过计算填写下表：‎ 正方形CEFG的边长 ‎1‎ ‎3‎ ‎4‎ ‎△BFD的面积 ‎（2）若正方形CEFG的边长为a，正方形ABCD的边长为b，猜出S△BFD的大小，并结合图③证明你的猜想。‎ ‎【答案】‎ ‎66．（2010四川达州）如图8，将一矩形纸片ABCD折叠，使点C与点A重合，点D落在点E处，折痕为MN，图中有全等三角形吗？若有，请找出并证明.‎ 图8‎ ‎【答案】解：有,△ABN≌△AEM.‎ 证明：∵四边形ABCD是矩形,‎ ‎∴AB=DC，∠B=∠C=∠DAB=90°‎ ‎∵四边形NCDM翻折得到四边形NAEM，‎ ‎∴AE=CD，∠E=∠D=90°,∠EAN=∠C=90°‎ ‎∴AB=AE，∠B=∠E，‎ ‎∠DAB=∠EAN，‎ 即：∠BAN+∠NAM=∠EAM+∠NAM，‎ ‎∴∠BAN=∠EAM.‎ 在△ABN与△AEM中，‎ ‎∴△ABN≌△AEM.‎ ‎67．（2010广东清远）如图6，在菱形ABCD中，∠A=60°，E、F分别是AD、CD上的两点，且AE=DF.‎ 求证：△ABE≌△DBF.‎ 图6‎ 证明：∵四边形ABCD是菱形，‎ ‎∴AB=BC=CD=DA.‎ 又∵∠A=60°，‎ ‎∴△ABD和△BCD都是等边三角形.‎ ‎∴AB=DB，∠A=∠BDF = 60°.‎ 又∵AE=DF，‎ ‎∴△ABE≌△DBF.‎ ‎68．（2010内蒙赤峰）两块完全相同的三角板I（△ABC）和Ⅱ（△A’B’C’）如图（1）所示放置在同一平面上 ‎（∠C=∠C’=90o，∠ABC=∠A’B’C’ =60 o），斜边重合，若三角板Ⅱ不动，三角板I在三角板Ⅱ所在的平面上向右滑动，图（2）是滑动过程中的一个位置。‎ ‎（1）连结BC’、B’C，（图（2）），求证△A’BC’≌△AB’C。‎ ‎（2）三角板I滑动到什么位置（点B’落在AB边的什么位置）时，四边形BCB’C’是菱形？‎ 说明理由。‎ ‎【答案】‎ ‎69．（2010广西百色）已知矩形中，对角线、相交于点，、是对角线上的两点，且.‎ ‎（1）按边分类，是三角形；‎ ‎（2）猜想线段、的大小关系，并证明你的猜想.‎ 第22题 ‎【答案】（1）等腰 …………………………………………2′‎ ‎ （2）猜想：…………………………1′‎ 证法一：∵四边形是矩形 ‎∴∥且=………………1′‎ ‎∴∠=∠…………………1′‎ ‎∵=‎ ‎∴≌（） ………2‎ ‎∴……………1′‎ ‎ 证法二：∵四边形是矩形 ‎∴‎ ‎∵=∴‎ ‎ 又∠=∠‎ ‎∴≌ ()‎ ‎∴‎ ‎ 证法三：如图，连结、‎ ‎ 由是矩形得 ‎∵=∴‎ ‎∴四边形是平行四边形. ∴‎ ‎70．（2010湖北黄石）如图，正方形ABCD中，E、F分别是AB、BC边上的点，且AE＝BF，求证AF⊥DE.‎ ‎【答案】‎