中考二次函数面积最值问题含答案 7页

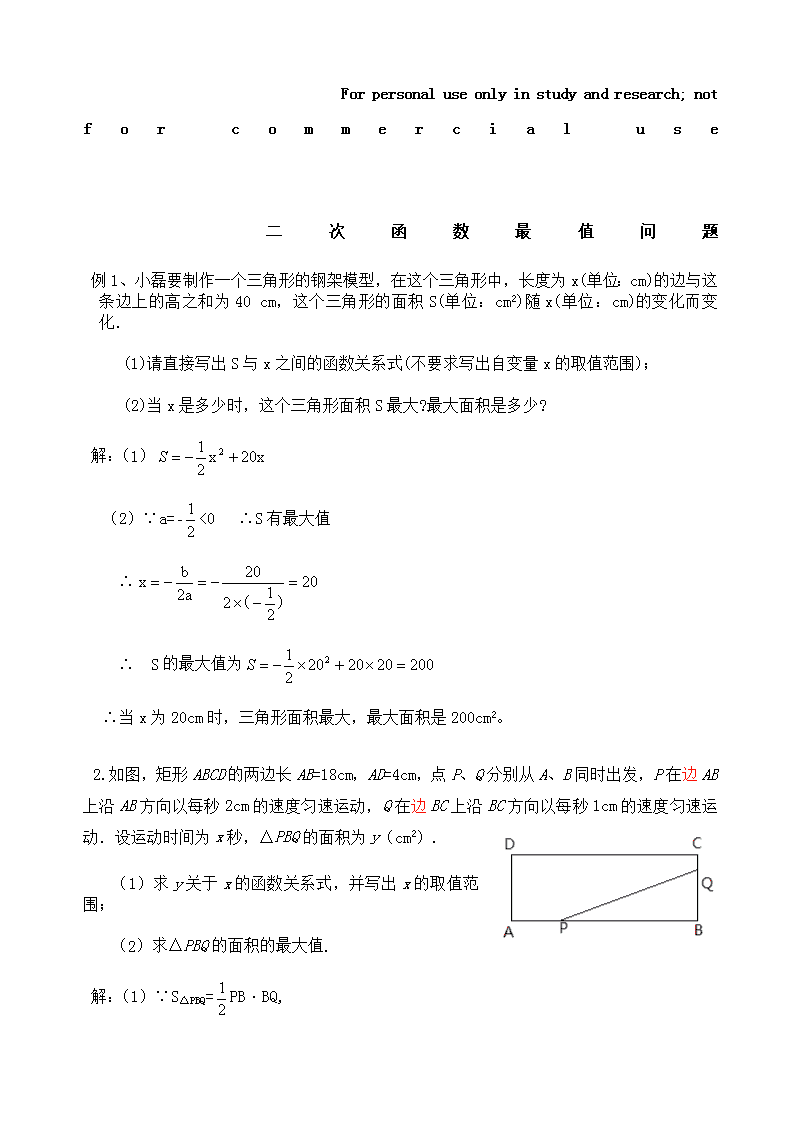
For personal use only in study and research; not for commercial use 膅二次函数最值问题 羄例1、小磊要制作一个三角形的钢架模型，在这个三角形中，长度为x(单位：cm)的边与这条边上的高之和为40 cm，这个三角形的面积S(单位：cm2)随x(单位：cm)的变化而变化．‎ 荿 (1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围)；‎ 芇 (2)当x是多少时，这个三角形面积S最大?最大面积是多少?‎ 袅解：（1） ‎ 螁（2）∵a=<0 ∴S有最大值 螂∴‎ 蚆∴ S的最大值为 蚅∴当x为20cm时，三角形面积最大，最大面积是200cm2。‎ 袃2.如图，矩形ABCD的两边长AB=18cm，AD=4cm，点P、Q分别从A、B同时出发，P在边AB上沿AB方向以每秒2cm的速度匀速运动，Q在边BC上沿BC方向以每秒1cm的速度匀速运动．设运动时间为x秒，△PBQ的面积为y（cm2）.‎ 袀（1）求y关于x的函数关系式，并写出x的取值范围；‎ 肆（2）求△PBQ的面积的最大值.‎ 莆解：（1）∵S△PBQ=PB·BQ, ‎ 袄PB=AB－AP=18－2x，BQ=x，‎ 羈∴y=（18－2x）x，即y=－x2+9x（0