湖北高考数学理试题及解析 12页

‎2013年湖北省数学高考试题（理）‎ ‎ ‎ 一．选择题 ‎ ‎1．在复平面内，复数（为虚数单位）的共轭复数对应的点位于（ ）‎ ‎ A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 ‎2．已知全集为，集合，，则（ ）‎ ‎ A. B. ‎ ‎ C. D.‎ ‎3．在一次跳伞训练中，甲．乙两位学员各跳一次，设命题是“甲降落在指定范围”，是“乙降落在指定范围”，则命题“至少有一位学员没有降落在指定范围”可表示为（ ）‎ ‎ A. B. C. D.‎ ‎4．将函数的图像向左平移个长度单位后，所得到的图像关于轴对称，则的最小值是（ ） ‎ A. B. C. D. ‎ ‎5．已知，则双曲线与的（ ）‎ A.实轴长相等 B.虚轴长相等 C.焦距相等 D. 离心率相等 ‎6．已知点．．．，则向量在方向上的投影为（ ）‎ ‎ A. B. C. D.‎ ‎7．一辆汽车在高速公路上行驶，由于遇到紧急情况而刹车，以速度（的单位：， 的单位：）行驶至停止。在此期间汽车继续行驶的距离（单位;）是（ ）‎ A. B. C. D. 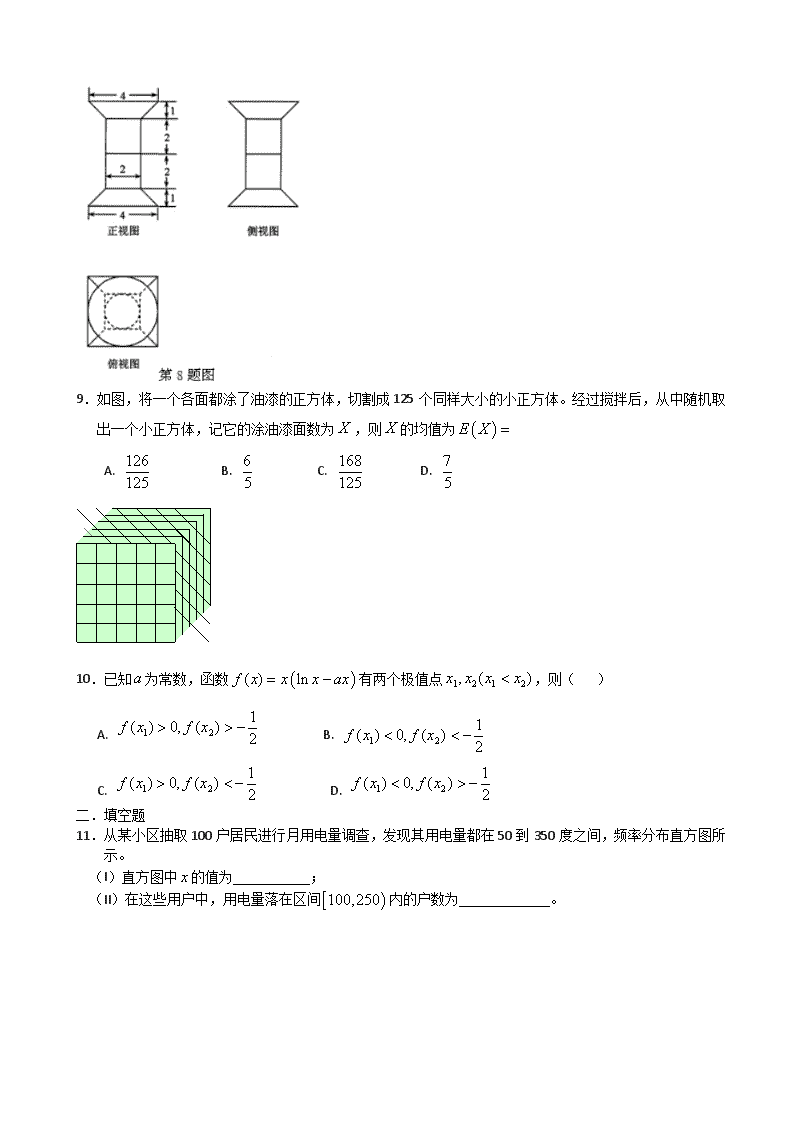‎ ‎8．一个几何体的三视图如图所示，该几何体从上到下由四个简单几何体组成，其体积分别记为，，，，上面两个简单几何体均为旋转体，下面两个简单几何体均为多面体，则有（ ）‎ ‎ A. B. C. D. 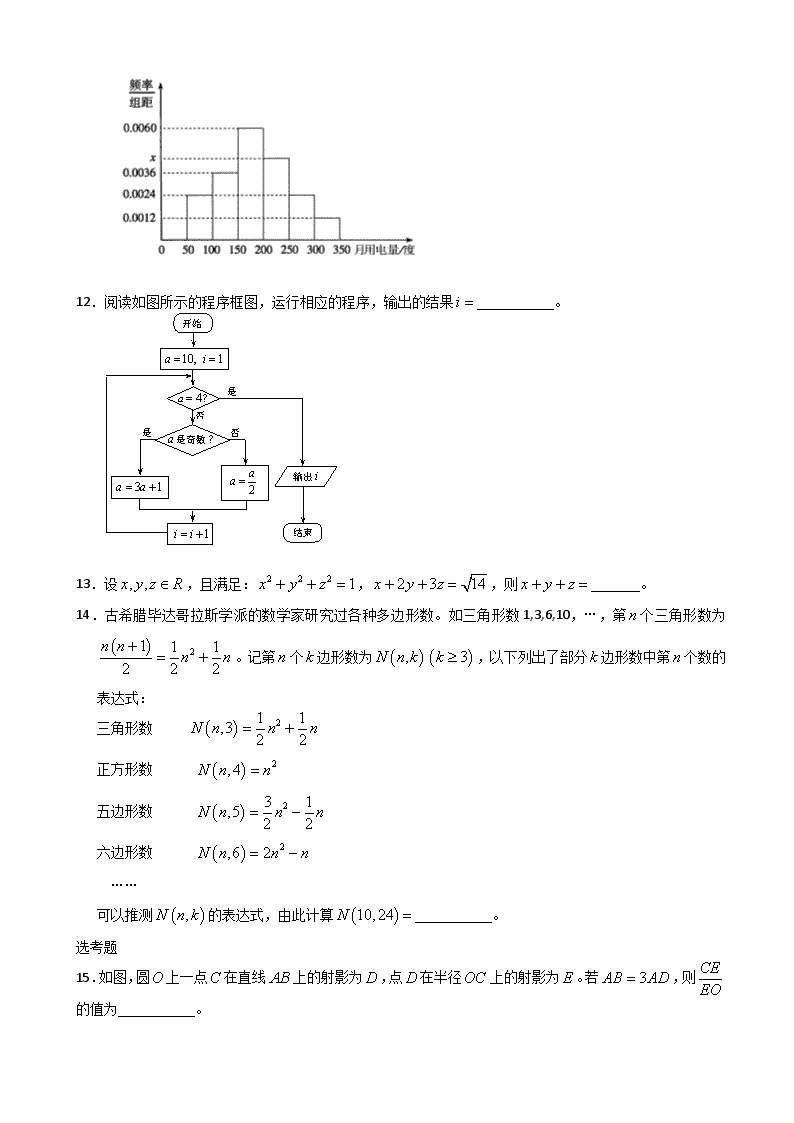‎ ‎ ‎ ‎9．如图，将一个各面都涂了油漆的正方体，切割成125个同样大小的小正方体。经过搅拌后，从中随机取出一个小正方体，记它的涂油漆面数为，则的均值为 ‎ A. B. C. D. ‎ ‎10．已知为常数，函数有两个极值点，则（ ）‎ ‎ A. B. ‎ ‎ C. D. ‎ 二．填空题 ‎11．从某小区抽取100户居民进行月用电量调查，发现其用电量都在50到350度之间，频率分布直方图所示。‎ ‎（I）直方图中的值为 ；‎ ‎（II）在这些用户中，用电量落在区间内的户数为 。‎ ‎ ‎ ‎12．阅读如图所示的程序框图，运行相应的程序，输出的结果 。‎ 否 开始 是 结束 是奇数 是 否 输出 ‎13．设，且满足：，，则 。‎ ‎14．古希腊毕达哥拉斯学派的数学家研究过各种多边形数。如三角形数1,3,6,10，…，第个三角形数为。记第个边形数为，以下列出了部分边形数中第个数的表达式：‎ 三角形数 ‎ 正方形数 ‎ 五边形数 ‎ 六边形数 ‎ ‎ ……‎ 可以推测的表达式，由此计算 。‎ 选考题 ‎15．如图，圆上一点在直线上的射影为，点在半径上的射影为。若，则的值为 。‎ 第15题图 ‎16．在直角坐标系中，椭圆的参数方程为。在极坐标系（与直角坐标系取相同的长度单位，且以原点为极点，以轴正半轴为极轴）中，直线与圆的极坐标方程分别为与。若直线经过椭圆的焦点，且与圆相切，则椭圆的离心率为 。‎ 三．解答题 ‎17．在中，角，，对应的边分别是，，。已知。‎ ‎（I）求角的大小；‎ ‎（II）若的面积，，求的值。‎ ‎18．已知等比数列满足：，。‎ ‎（I）求数列的通项公式；‎ ‎（II）是否存在正整数，使得？若存在，求的最小值；若不存在，说明理由。‎ ‎19．如图，是圆的直径，点是圆上异于的点，直线平面，，分别是，的中点。‎ ‎（I）记平面与平面的交线为，试判断直线与平面的位置关系，并加以证明；‎ ‎（II）设（I）中的直线与圆的另一个交点为，且点满足。记直线与平面所成的角为，异面直线与所成的角为，二面角的大小为，求证：。‎ 第19题图 ‎20．假设每天从甲地去乙地的旅客人数是服从正态分布的随机变量。记一天中从甲地去乙地的旅客人数不超过900的概率为。‎ ‎（I）求的值；（参考数据：若，有，，。）‎ ‎（II）某客运公司用．两种型号的车辆承担甲．乙两地间的长途客运业务，每车每天往返一次，．两种车辆的载客量分别为36人和60人，从甲地去乙地的运营成本分别为1600元/辆和2400元/辆。公司拟组建一个不超过21辆车的客运车队，并要求型车不多于型车7辆。若每天要以不小于的概率运完从甲地去乙地的旅客，且使公司从甲地去乙地的运营成本最小，那么应配备型车．型车各多少辆？‎ ‎21．如图，已知椭圆与的中心在坐标原点，长轴均为且在轴上，短轴长分别为，，过原点且不与轴重合的直线与，的四个交点按纵坐标从大到小依次为，，，。记，和的面积分别为和。‎ ‎（I）当直线与轴重合时，若，求的值；‎ ‎（II）当变化时，是否存在与坐标轴不重合的直线，使得？并说明理由。‎ 第21题图 ‎22．设是正整数，为正有理数。‎ ‎（I）求函数的最小值；‎ ‎（II）证明：；‎ ‎（III）设，记为不小于的最小整数，例如，，。令，求的值。‎ ‎（参考数据：，，，）‎ 参考答案 一、选择题 ‎1．D解：，。‎ ‎2．C 解：，，。‎ ‎3．A 解：“至少有一位学员没有降落在指定范围”即：“甲或乙没有降落在指定范围内”。‎ ‎4．B解：的图像向左平移个长度单位后变成，所以的最小值是。故选B。‎ ‎5．D解：双曲线的离心率是，双曲线的离心率是，故选D ‎6．A解：，，，故选A。‎ ‎7．C解：令 ，则。汽车刹车的距离是，故选C。‎ ‎8．C解：C 由柱体和台体的体积公式可知选C ‎9．B解：三面涂有油漆的有8块，两面涂有油漆的有36块，一面涂有油漆的有54块，没有涂有油漆的有27块，所以。故选B。‎ ‎10．D解：令得，。‎ 又，。，‎ ‎11．；70 解：，‎ ‎ ‎ ‎12． 5 解：5 程序框图运行过程如表所示：‎ i ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ a ‎10‎ ‎5‎ ‎16‎ ‎8‎ ‎4‎ ‎13． 解：由柯西不等式知，结合已知条件得，从而解得，。 ‎ ‎14．1000 解：观察和前面的系数，可知一个成递增的等差数列另一个成递减的等差数列，故， ‎ ‎15．8 解：由射影定理知 ‎16． 解：直线的方程是，作出图形借助直线的斜率可得，所以，‎ ‎17．解：（I）由已知条件得：‎ ‎，解得，角 ‎（II），由余弦定理得：，‎ ‎18．解：（I）由已知条件得：，又，，‎ 所以数列的通项或 ‎（II）若，，不存在这样的正整数；‎ 若，，不存在这样的正整数。‎ ‎19．解： ‎ ‎【解析与答案】‎ ‎（I）直线∥平面PAC,证明如下：‎ 连接EF,因为E,F分别是PA,PC的中点，所以EF∥AC.‎ 又EF平面ABC,且AC平面ABC,所以EF∥平面ABC.‎ 而EF平面BEF,且平面BEF∩平面ABC=,所以EF∥.‎ ‎ 因为平面PAC,EF平面PAC,所以直线∥平面PAC.‎ ‎（II）(综合法)如图1，连接BD，由可知交线即为直线BD，且∥AC.‎ 因为AB是的直线，所以AC⊥BC,于是⊥BC.‎ 已知PC⊥平面ABC,而平面ABC，所以PC⊥.‎ 而PC∩BC=C,所以⊥平面PBC.‎ 连接BE,BF,因为BF平面PBC,所以⊥BF.‎ 故∠CBF就是二面角的平面角，即∠CBF=β.‎ 由，作DQ∥CP,且DQ=CP.‎ 连接PQ,DF,因为F是CP的中点，CP=2PF,所以DQ=PF,‎ 从而四边形DQPF是平行四边形，PQ∥FD.‎ 连接CD,因为PC⊥平面ABC,所以CD是FD在平面ABC内的射影，‎ 故∠CDF就是直线PQ与平面ABC所成的角，即∠CDF=.‎ 又BD⊥平面PBC,有BD⊥BF,知∠BDF为锐角，‎ 故∠BDF为异面直线PQ与EF所成的角，即∠BDF=α，‎ 于是在Rt△DCF,Rt△FBD,Rt△BCF中，分别可得 ‎,,,从而，即.‎ ‎（II）(向量法)如图2，由，作DQ∥CP,且DQ=CP.‎ 连接PQ,EF,BE,BF,BD,由（I）可知交线即为直线BD.‎ 以点C为原点，向量所在直线分别为轴，建立如图所示的空间直角坐标系，‎ 设，，则有C(0，0，0),A(,0，0)，B(0，,0)，P(0，0，),Q(),‎ E(),F(0，0，). 于是，，.‎ 所以，从而.‎ 又取平面ABC的一个法向量为，可得，‎ 设平面BEF的一个法向量为，‎ 所以由，可得，取.‎ 于是，从而.‎ 故，即.‎ ‎20．解：（I）‎ ‎（II）设配备型车辆，型车辆，运营成本为元，由已知条件得 ‎，而 作出可行域，得到最优解。‎ 所以配备型车5辆，型车12辆可使运营成本最小。‎ ‎21．解：（I），‎ 解得：（舍去小于1的根）‎ ‎（II）设椭圆，，直线：‎ 同理可得，‎ 又和的的高相等 如果存在非零实数使得，则有，‎ 即：，解得 当时，，存在这样的直线；当时，，不存在这样的直线。‎ ‎22．证明：（I）‎ 在上单减，在上单增。‎ ‎（II）由（I）知：当时，（就是伯努利不等式了）‎ 所证不等式即为：‎ 若，则 ‎ …………①‎ ‎，‎ ‎，故①式成立。‎ 若，显然成立。‎ ‎ …………②‎ ‎，‎ ‎，故②式成立。‎ 综上可得原不等式成立。‎ ‎（III）由（II）可知：当时，‎ ‎ ‎