高考江西卷文科数学试题及参考答案 14页

‎2006高等学校全国统一数学文试题（江西卷）‎ 一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．已知集合，，则等于（　　）‎ Ａ． Ｂ． ‎ Ｃ． Ｄ．‎ ‎2．函数的最小正周期为（　　）‎ Ａ． Ｂ． Ｃ． Ｄ．‎ ‎3．在各项均不为零的等差数列中，若，则（　　）‎ Ａ． Ｂ． Ｃ． Ｄ．‎ ‎4．下列四个条件中，是的必要不充分条件的是（　　）‎ Ａ．，‎ Ｂ．，‎ Ｃ．为双曲线， ‎ Ｄ．，‎ ‎5．对于上可导的任意函数，若满足，则必有（　　）‎ Ａ． Ｂ．‎ Ｃ． Ｄ．‎ ‎6．若不等式对一切成立，则的最小值为（　　）‎ Ａ． Ｂ． Ｃ． Ｄ．‎ ‎7．在的二项展开式中，若常数项为，则等于（　　）‎ Ａ． Ｂ． Ｃ． Ｄ．‎ ‎8．袋中有40个小球，其中红色球16个、蓝色球12个，白色球8个，黄色球4个，从中随机抽取10个球作成一个样本，则这个样本恰好是按分层抽样方法得到的概率为（　　）‎ Ａ． Ｂ． ‎ Ｃ． Ｄ．‎ ‎9．如果四棱锥的四条侧棱都相等，就称它为“等腰四棱锥”，四条侧棱称为它的腰，以下4个命题中，假命题是（　　）‎ Ａ．等腰四棱锥的腰与底面所成的角都相等 ‎ Ｂ．等腰四棱锥的侧面与底面所成的二面角都相等或互补 Ｃ．等腰四棱锥的底面四边形必存在外接圆 Ｄ．等腰四棱锥的各顶点必在同一球面上 ‎10．已知等差数列的前项和为，若，且三点共线（该直线不过点），则等于（　　　）‎ Ａ．100 Ｂ．101 Ｃ．200 Ｄ．201‎ ‎11．为双曲线的右支上一点，，分别是圆和上的点，则的最大值为（　　）‎ Ａ． Ｂ． Ｃ． Ｄ．‎ ‎4‎ ‎4‎ ‎8‎ ‎12‎ ‎16‎ ‎20‎ ‎24‎ ‎ 图（1）‎ ‎4‎ ‎4‎ ‎8‎ ‎16‎ ‎20‎ Ｂ ‎24‎ ‎12‎ ‎16‎ ‎4‎ ‎4‎ ‎8‎ ‎12‎ ‎24‎ Ａ ‎16‎ ‎20‎ ‎16‎ ‎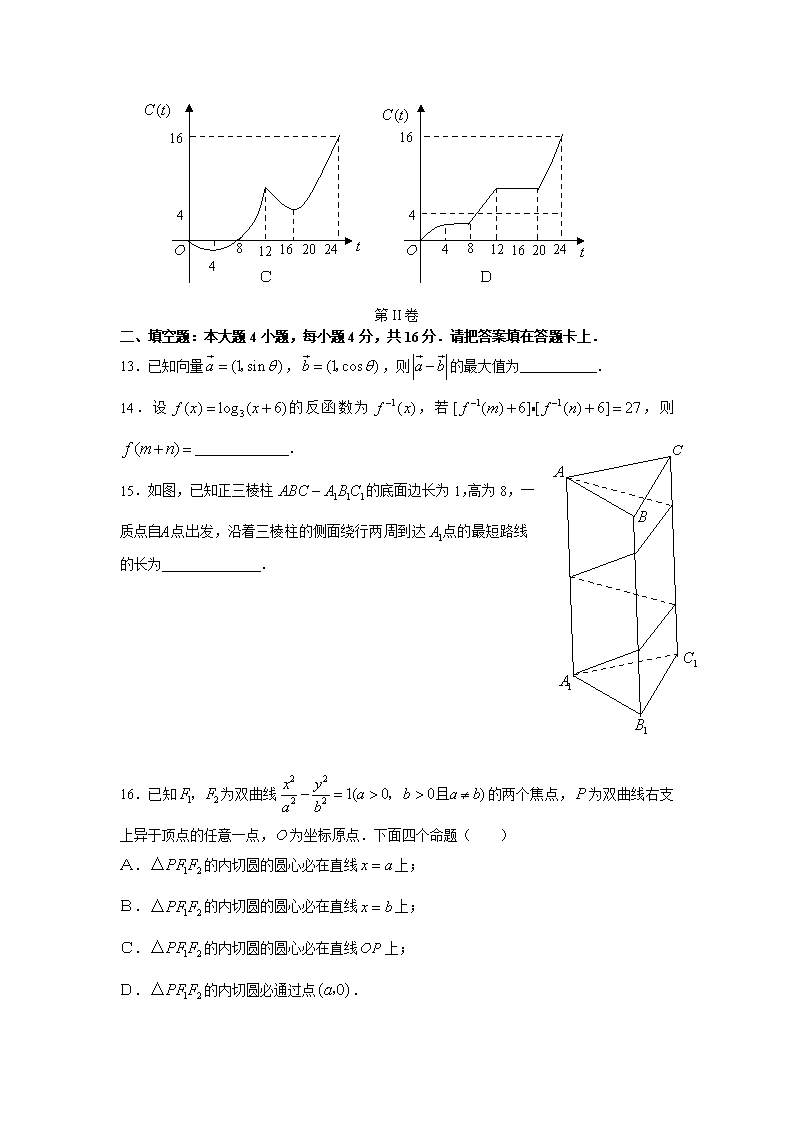12．某地一天内的气温（单位：℃）与时刻（单位：时）之间的关系如图（1）所示，令表示时间段内的温差（即时间段内最高温度与最低温度的差）．与之间的函数关系用下列图象表示，则正确的图象大致是（　　）‎ ‎4‎ ‎4‎ ‎8‎ ‎16‎ ‎20‎ Ｃ ‎24‎ ‎12‎ ‎16‎ ‎4‎ ‎4‎ ‎8‎ ‎12‎ ‎24‎ Ｄ ‎16‎ ‎20‎ ‎16‎ 第II卷 二、填空题：本大题4小题，每小题4分，共16分．请把答案填在答题卡上．‎ ‎13．已知向量，，则的最大值为 ．‎ ‎14．设的反函数为，若，则 ．‎ ‎15．如图，已知正三棱柱的底面边长为1，高为8，一质点自点出发，沿着三棱柱的侧面绕行两周到达点的最短路线的长为 ．‎ ‎16．已知为双曲线的两个焦点，为双曲线右支上异于顶点的任意一点，为坐标原点．下面四个命题（　　）‎ Ａ．的内切圆的圆心必在直线上；‎ Ｂ．的内切圆的圆心必在直线上；‎ Ｃ．的内切圆的圆心必在直线上；‎ Ｄ．的内切圆必通过点．‎ 其中真命题的代号是 （写出所有真命题的代号）．‎ 三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．‎ ‎17．（本小题满分12分）‎ 已知函数在与时都取得极值．‎ ‎（1）求的值及函数的单调区间；‎ ‎（2）若对，不等式恒成立，求的取值范围．‎ ‎18．（本小题满分12分）‎ 某商场举行抽奖促销活动，抽奖规则是：从装有9个白球、1个红球的箱子中每次随机地摸出一个球，记下颜色后放回，摸出一个红球获得二得奖；摸出两个红球获得一等奖．现有甲、乙两位顾客，规定：甲摸一次，乙摸两次．求 ‎（1）甲、乙两人都没有中奖的概率；‎ ‎（2）甲、两人中至少有一人获二等奖的概率．‎ ‎19．（本小题满分12分）‎ 在锐角中，角所对的边分别为，已知，‎ ‎（1）求的值；‎ Ａ Ｏ Ｅ Ｃ Ｂ ‎（2）若，，求的值．‎ ‎20．（本小题满分12分）‎ 如图，已知三棱锥的侧棱两两垂直，且，，是的中点．‎ ‎（1）求点到面的距离；‎ ‎（2）求异面直线与所成的角；‎ ‎（3）求二面角的大小．‎ ‎21．（本小题满分12分）‎ O P A F B D x y 如图，椭圆的右焦点为，过点的一动直线绕点转动，并且交椭圆于两点，为线段的中点．‎ ‎（1）求点的轨迹的方程；‎ ‎（2）若在的方程中，令，‎ ‎．‎ 设轨迹的最高点和最低点分别为和．当为何值时，为一个正三角形？‎ ‎22．（本小题满分14分）‎ 已知各项均为正数的数列，满足：，且，．‎ ‎（1）求数列的通项公式；‎ ‎（2）设，，求，并确定最小正整数，使为整数．‎ ‎2006年普通高等学校招生全国统一考试（江西卷）‎ 文科数学（编辑：ahuazi）‎ 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷1至2页。第Ⅱ卷3至4页。全卷满分150分，考试时间120分钟。‎ 考生注意事项：‎ ‎1.答题前，务必在试题卷、答题卡规定的地方填写自己的座位号、姓名，并认真核对答题卡上所粘贴的条形码中“座位号、姓名、科类”与本人座位号、姓名、科类是否一致。‎ ‎2．答第Ⅰ卷时，每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。‎ ‎3．答第Ⅱ卷时，必须用0.5毫米墨水签字笔在答题卡上书写。在试题卷上作答无效。‎ ‎4．考试结束，监考人员将试题卷和答题卡一并收回。‎ 参考公式：‎ 如果时间A、B互斥，那么 如果时间A、B相互独立，那么 如果事件A在一次试验中发生的概率是P，那么n次独立重复试验中恰好发生k次的概率 球的表面积公式，其中R表示球的半径 球的体积公式，其中R表示球的半径 一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．已知集合，，则等于（C　　）‎ Ａ． Ｂ． ‎ Ｃ． Ｄ．‎ 解：P＝｛x|x³1或x£0｝，Q＝｛x|x>1｝故选C ‎2．函数的最小正周期为（B　　）‎ Ａ． Ｂ． Ｃ． Ｄ．‎ 解：T＝，故选B ‎3．在各项均不为零的等差数列中，若，则（　A　）‎ Ａ． Ｂ． Ｃ． Ｄ．‎ 解：设公差为d，则an＋1＝an＋d，an－1＝an－d，由可得2an－＝0，解得an＝2（零解舍去），故2×（2n－1）－4n＝－2，故选A ‎4．下列四个条件中，是的必要不充分条件的是（　D　）‎ Ａ．，‎ Ｂ．，‎ Ｃ．为双曲线， ‎ Ｄ．，‎ 解：A. p不是q的充分条件，也不是必要条件；B. p是q的充要条件；C. p是q的充分条件，不是必要条件；D.正确 ‎5．对于上可导的任意函数，若满足，则必有（C　　）‎ Ａ． Ｂ．‎ Ｃ． Ｄ．‎ 解：依题意，当x³1时，f¢（x）³0，函数f（x）在（1，＋¥）上是增函数；当x<1时，f¢（x）£0，f（x）在（－¥ ‎，1）上是减函数，故f（x）当x＝1时取得最小值，即有 f（0）³f（1），f（2）³f（1），故选C ‎6．若不等式对一切成立，则的最小值为（　C　）‎ Ａ． Ｂ． Ｃ． Ｄ．‎ 解：设f（x）＝x2＋ax＋1，则对称轴为x＝‎ 若³，即a£－1时，则f（x）在〔0，〕上是减函数，应有f（）³0Þ ‎－£x£－1‎ 若£0，即a³0时，则f（x）在〔0，〕上是增函数，应有f（0）＝1>0恒成立，故a³0‎ 若0££，即－1£a£0，则应有f（）＝恒成立，故－1£a£0‎ 综上，有－£a故选C ‎7．在的二项展开式中，若常数项为，则等于（　B　）‎ Ａ． Ｂ． Ｃ． Ｄ．‎ 解：，由解得n＝6故选B ‎8．袋中有40个小球，其中红色球16个、蓝色球12个，白色球8个，黄色球4个，从中随机抽取10个球作成一个样本，则这个样本恰好是按分层抽样方法得到的概率为（A　　）‎ Ａ． Ｂ． ‎ Ｃ． Ｄ．‎ 解：依题意，各层次数量之比为4:3:2:1，即红球抽4个，蓝球抽3个，白球抽2个，黄球抽一个，故选A ‎9．如果四棱锥的四条侧棱都相等，就称它为“等腰四棱锥”，四条侧棱称为它的腰，以下4个命题中，假命题是（　B　）‎ Ａ．等腰四棱锥的腰与底面所成的角都相等 ‎ Ｂ．等腰四棱锥的侧面与底面所成的二面角都相等或互补 Ｃ．等腰四棱锥的底面四边形必存在外接圆 Ｄ．等腰四棱锥的各顶点必在同一球面上 解：因为“等腰四棱锥”的四条侧棱都相等，所以它的顶点在底面的射影到底面的四个顶点的距离相等，故A，C正确，且在它的高上必能找到一点到各个顶点的距离相等，故D正确，B不正确，如底面是一个等腰梯形时结论就不成立。故选B ‎10．已知等差数列的前项和为，若，且三点共线（该直线不过点），则等于（A　　　）‎ Ａ．100 Ｂ．101 Ｃ．200 Ｄ．201‎ 解：依题意，a1＋a200＝1，故选A ‎11．为双曲线的右支上一点，，分别是圆和上的点，则的最大值为（　D　）‎ Ａ． Ｂ． Ｃ． Ｄ．‎ 解：设双曲线的两个焦点分别是F1（－5，0）与F2（5，0），则这两点正好是两圆的圆心，当且仅当点P与M、F1三点共线以及P与N、F2三点共线时所求的值最大，此时 ‎|PM|－|PN|＝（|PF1|－2）－（|PF2|－1）＝10－1＝9故选B ‎4‎ ‎4‎ ‎8‎ ‎12‎ ‎16‎ ‎20‎ ‎24‎ ‎ 图（1）‎ ‎4‎ ‎4‎ ‎8‎ ‎16‎ ‎20‎ Ｂ ‎24‎ ‎12‎ ‎16‎ ‎4‎ ‎4‎ ‎8‎ ‎12‎ ‎24‎ Ａ ‎16‎ ‎20‎ ‎16‎ ‎12．某地一天内的气温（单位：℃）与时刻（单位：时）之间的关系如图（1）所示，令表示时间段内的温差（即时间段内最高温度与最低温度的差）．与之间的函数关系用下列图象表示，则正确的图象大致是（D　　）‎ ‎4‎ ‎4‎ ‎8‎ ‎16‎ ‎20‎ Ｃ ‎24‎ ‎12‎ ‎16‎ ‎4‎ ‎4‎ ‎8‎ ‎12‎ ‎24‎ Ｄ ‎16‎ ‎20‎ ‎16‎ 解：结合图象及函数的意义可得。‎ 第II卷 二、填空题：本大题4小题，每小题4分，共16分．请把答案填在答题卡上．‎ ‎13．已知向量，，则的最大值为 解：＝|sinq－cosq|＝|sin（q－）|£|‎ ‎14．设的反函数为，若，则 2 ．‎ 解：f－1（x）＝3x－6故〔f－1（m）＋6〕·〔f－1（x）＋6〕＝3m·3n＝3m ＋n＝27‎ m＋n＝3f（m＋n）＝log3（3＋6）＝2‎ ‎15．如图，已知正三棱柱的底面边长为1，高为8，一质点自点出发，沿着三棱柱的侧面绕行两周到达点的最短路线的长为 10 ．‎ 解：将正三棱柱沿侧棱CC1展开，‎ 其侧面展开图如图所示，由图中路线可得结论。‎ ‎16．已知为双曲线的两个焦点，为双曲线右支上异于顶点的任意一点，为坐标原点．下面四个命题（　　）‎ Ａ．的内切圆的圆心必在直线上；‎ Ｂ．的内切圆的圆心必在直线上；‎ Ｃ．的内切圆的圆心必在直线上；‎ Ｄ．的内切圆必通过点．‎ 其中真命题的代号是 （A）、（D） （写出所有真命题的代号）．‎ 解：设的内切圆分别与PF1、PF2切于点A、B，与F1F2切于点M，则|PA|＝|PB|，|F1A|＝|F1M|，|F2B|＝|F2M|，又点P在双曲线右支上，所以|PF1|－|PF2|＝2a，故|F1M|－|F2M|＝2a，而|F1M|＋|F2M|＝2c，设M点坐标为（x，0），则由|F1M|－|F2M|＝2a可得（x＋c）－（c－x）＝2a解得x＝a，显然内切圆的圆心与点M的连线垂直于x轴，故A、D正确。‎ 三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．‎ ‎17．（本小题满分12分）‎ 已知函数在与时都取得极值．‎ ‎（1）求的值及函数的单调区间；‎ ‎（2）若对，不等式恒成立，求的取值范围．‎ 解：（1）f（x）＝x3＋ax2＋bx＋c，f¢（x）＝3x2＋2ax＋b 由f¢（）＝，f¢（1）＝3＋2a＋b＝0得 a＝，b＝－2‎ f¢（x）＝3x2－x－2＝（3x＋2）（x－1），函数f（x）的单调区间如下表：‎ x ‎（－¥，－）‎ ‎－‎ ‎（－，1）‎ ‎1‎ ‎（1，＋¥）‎ f¢（x）‎ ‎＋‎ ‎0‎ ‎－‎ ‎0‎ ‎＋‎ f（x）‎ 极大值 ¯ 极小值 所以函数f（x）的递增区间是（－¥，－）与（1，＋¥）‎ 递减区间是（－，1）‎ ‎（2）f（x）＝x3－x2－2x＋c，xÎ〔－1，2〕，当x＝－时，f（x）＝＋c 为极大值，而f（2）＝2＋c，则f（2）＝2＋c为最大值。‎ 要使f（x）f（2）＝2＋c 解得c<－1或c>2‎ ‎18．（本小题满分12分）‎ 某商场举行抽奖促销活动，抽奖规则是：从装有9个白球、1个红球的箱子中每次随机地摸出一个球，记下颜色后放回，摸出一个红球获得二得奖；摸出两个红球获得一等奖．现有甲、乙两位顾客，规定：甲摸一次，乙摸两次．求 ‎（1）甲、乙两人都没有中奖的概率；‎ ‎（2）甲、两人中至少有一人获二等奖的概率．‎ 解：（1）P1＝‎ ‎（2）法一：P2＝‎ 法二：P2＝‎ 法三：P2＝1－‎ ‎19．（本小题满分12分）‎ 在锐角中，角所对的边分别为，已知，‎ ‎（1）求的值；‎ ‎（2）若，，求的值．‎ 解：（1）因为锐角△ABC中，A＋B＋C＝p，，所以cosA＝，则 ‎（2），则bc＝3。将a＝2，cosA＝，c＝代入余弦定理：中得解得b＝ ‎ ‎20．（本小题满分12分）‎ 如图，已知三棱锥的侧棱两两垂直，且，，是的中点．‎ ‎（1）求点到面的距离；‎ Ａ Ｏ Ｅ Ｃ Ｂ ‎（2）求异面直线与所成的角；‎ ‎（3）求二面角的大小．‎ 解：（1）取BC的中点D，连AD、OD 因为OB＝OC，则OD^BC、AD^BC，BC^面OAD.‎ 过O点作OH^AD于H，则OH^面ABC，OH的长就 是所求的距离. 又BC＝2，OD＝‎ ‎＝，又OA^OB，OA^OC OA^面OBC，则OA^OD AD＝＝，在直角三角形OAD中，‎ 有OH＝‎ ‎（另解：由等体积变换法也可求得答案）‎ ‎（2）取OA的中点M，连EM、BM，则 EM//AC,ÐBEM是异面直线BE与AC 所成的角，易求得EM＝，BE＝，‎ BM＝.由余弦定理可求得cosÐBEM＝，‎ ÐBEM＝arccos ‎（3）连CM并延长交AB于F，连OF、EF.‎ 由OC^面OAB，得OC^AB，又OH^面ABC，所以CF^AB，EF^AB，则ÐEFC就是所求的二面角的平面角.‎ 作EG^CF于G，则EG＝OH＝，在Rt△OAB中，OF＝‎ 在Rt△OEF中，EF＝‎ sinÐEFG＝ÐEFG＝arcsin.（或表示为arccos）‎ 注：此题也可用空间向量的方法求解。‎ ‎21．（本小题满分12分）‎ O P A F B D x y 如图，椭圆的右焦点为，过点的一动直线绕点转动，并且交椭圆于两点，为线段的中点．‎ ‎（1）求点的轨迹的方程；‎ ‎（2）若在的方程中，令，‎ ‎．‎ 设轨迹的最高点和最低点分别为和．当为何值时，为一个正三角形？‎ 解：如图，（1）设椭圆Q：（a>b>0）‎ 上的点A（x1，y1）、B（x2，y2），又设P点坐标为P（x，y），则 ‎1°当AB不垂直x轴时，x1¹x2，‎ 由（1）－（2）得 b2（x1－x2）2x＋a2（y1－y2）2y＝0‎ ‎ ‎ 2x2＋a2y2－b2cx＝0…………（3）‎ ‎2°当AB垂直于x轴时，点P即为点F，满足方程（3）‎ 故所求点P的轨迹方程为：b2x2＋a2y2－b2cx＝0‎ ‎（2）因为轨迹H的方程可化为：‎ M（，），N（ ，－），F（c，0），使△MNF为一个正三角形时，则 tan＝＝，即a2＝3b2. 由于，‎ ‎，则1＋cosq＋sinq＝3 sinq，得q＝arctan ‎22．（本小题满分14分）‎ 已知各项均为正数的数列，满足：，且，．‎ ‎（1）求数列的通项公式；‎ ‎（2）设，，求，并确定最小正整数，使为整数．‎ 解：（1）条件可化为，因此｛‎ ‎｝为一个等比数列，其公比为2，首项为，所以＝…………1° 因an>0，由1°式解出an＝…………2° ‎（2）由1°式有Sn＋Tn＝‎ ‎＝‎ ‎＝‎ 为使Sn＋Tn＝为整数，当且仅当为整数.‎ 当n＝1,2时，显然Sn＋Tn不为整数，‎ 当n³3时，＝ ＝‎ 只需＝为整数，因为3n－1与3互质，所以 为9的整数倍.当n＝9时，＝13为整数，故n的最小值为9.‎