- 1.87 MB
- 2021-05-13 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
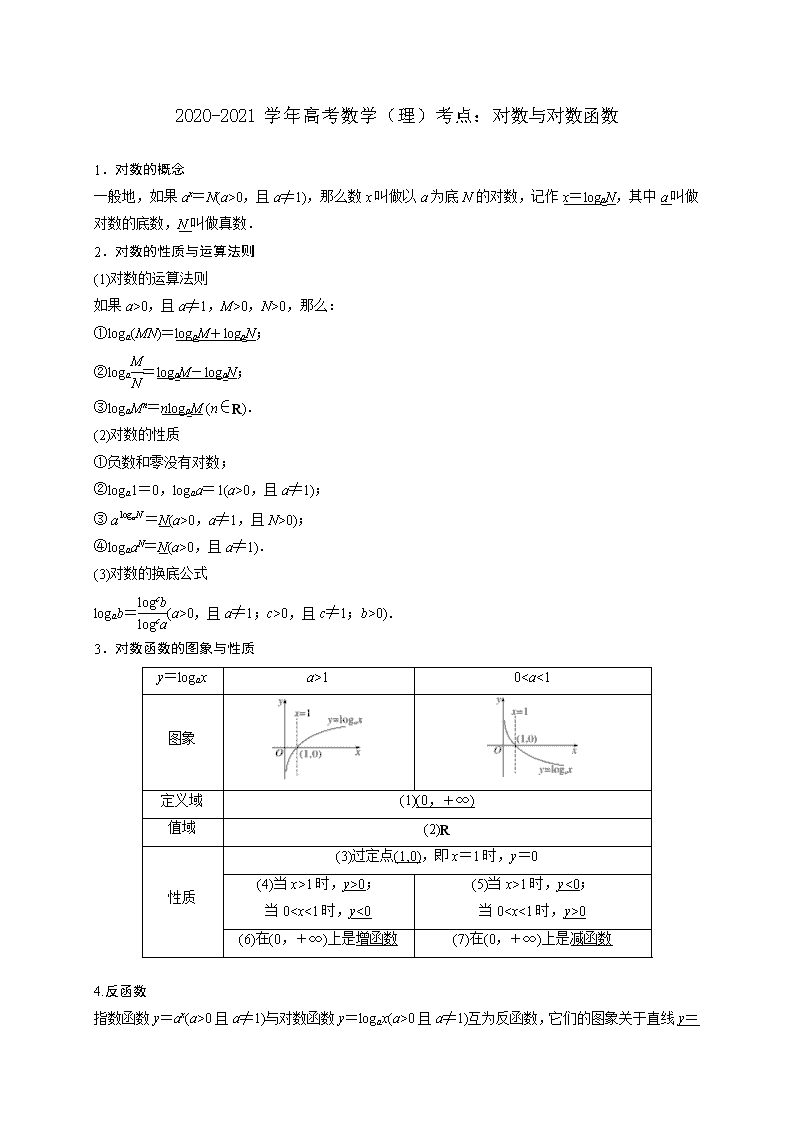
2020-2021学年高考数学(理)考点:对数与对数函数
1.对数的概念
一般地,如果ax=N(a>0,且a≠1),那么数x叫做以a为底N的对数,记作x=logaN,其中a叫做对数的底数,N叫做真数.
2.对数的性质与运算法则
(1)对数的运算法则
如果a>0,且a≠1,M>0,N>0,那么:
①loga(MN)=logaM+logaN;
②loga=logaM-logaN;
③logaMn=nlogaM (n∈R).
(2)对数的性质
①负数和零没有对数;
②loga1=0,logaa=1(a>0,且a≠1);
③=N(a>0,a≠1,且N>0);
④logaaN=N(a>0,且a≠1).
(3)对数的换底公式
logab=(a>0,且a≠1;c>0,且c≠1;b>0).
3.对数函数的图象与性质
y=logax
a>1
01时,y>0;
当01时,y<0;
当00
(6)在(0,+∞)上是增函数
(7)在(0,+∞)上是减函数
4.反函数
指数函数y=ax(a>0且a≠1)与对数函数y=logax(a>0且a≠1)互为反函数,它们的图象关于直线y=
x对称.
概念方法微思考
1.根据对数换底公式:①说出logab,logba的关系?
②化简.
提示 ①logab·logba=1;②=logab.
2.如图给出4个对数函数的图象.比较a,b,c,d与1的大小关系.
提示 0