高考数学小题狂练每题都附有详细解析 14页

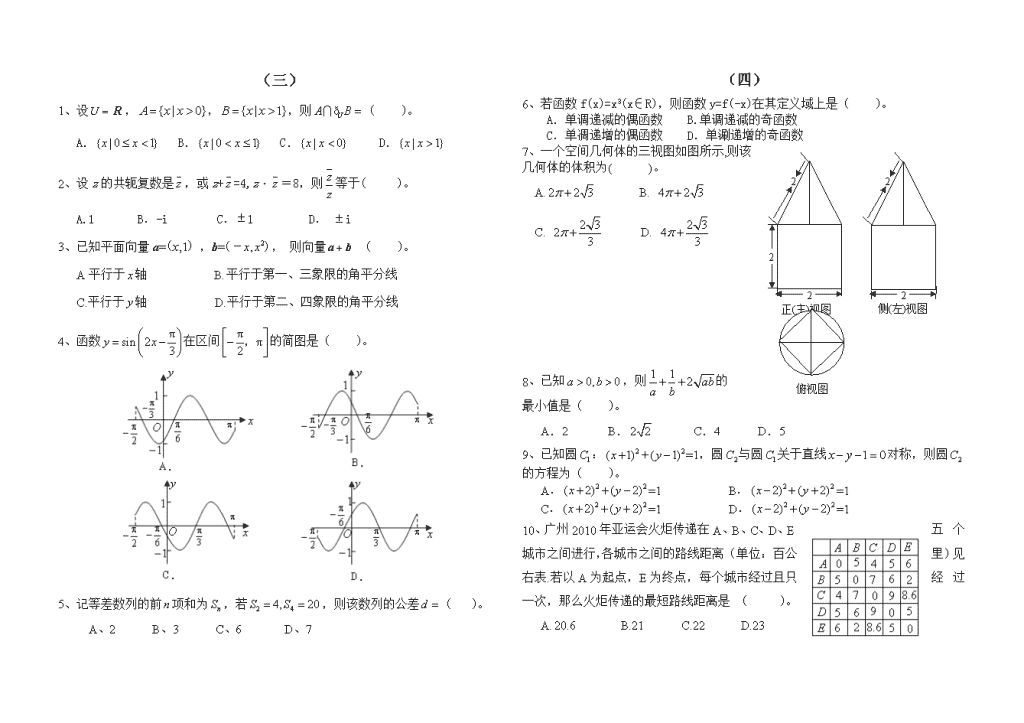
‎（一）‎ ‎1、设，，，则（ ）。‎ A． B． C． D． ‎ ‎2、设z的共轭复数是，或z+=4,z·＝8，则等于( )。‎ A.1　　　 B．-i 　C．±1 　D． ±i ‎3、已知平面向量a= ，b=， 则向量 （ ）。‎ A平行于轴 B.平行于第一、三象限的角平分线 ‎ C.平行于轴 D.平行于第二、四象限的角平分线 ‎ ‎4、函数在区间的简图是（　　）。‎ ‎5、记等差数列的前项和为，若，则该数列的公差（ ）。‎ A、2 B、‎3 C、6 D、7‎ ‎（二）‎ ‎6、若函数f(x)=x3(x∈R)，则函数y=f(-x)在其定义域上是（ ）。‎ ‎ A．单调递减的偶函数 B.单调递减的奇函数 ‎ C．单凋递增的偶函数 D．单涮递增的奇函数 ‎2 ‎ ‎2 ‎ 侧(左)视图 ‎ ‎2 ‎ ‎2 ‎ ‎2 ‎ 正(主)视图 ‎ ‎7、一个空间几何体的三视图如图所示,则该几何体的体积为( )。‎ A. B. ‎ C. D. ‎ 俯视图 ‎ ‎8、已知，则的 最小值是（ ）。‎ A．2 B． C．4 D．5‎ ‎9、已知圆：+=1，圆与圆关于直线对称，则圆的方程为（ ）。‎ A．+=1 B．+=1‎ C．+=1 D．+=1‎ ‎10、广州2010年亚运会火炬传递在A、B、C、D、E五个城市之间进行，各城市之间的路线距离（单位：百公里）见右表.若以A为起点，E为终点，每个城市经过且只经过一次，那么火炬传递的最短路线距离是 （ ）。‎ A. B‎.21 C.22 D.23 ‎ ‎（三）‎ ‎1、设，，，则（ ）。‎ A． B． C． D． ‎ ‎2、设z的共轭复数是，或z+=4,z·＝8，则等于( )。‎ A.1　　　 B．-i 　C．±1 　D． ±i ‎3、已知平面向量a= ，b=， 则向量 （ ）。‎ A平行于轴 B.平行于第一、三象限的角平分线 ‎ C.平行于轴 D.平行于第二、四象限的角平分线 ‎ ‎4、函数在区间的简图是（　　）。‎ ‎5、记等差数列的前项和为，若，则该数列的公差（ ）。‎ A、2 B、‎3 C、6 D、7‎ ‎（四）‎ ‎6、若函数f(x)=x3(x∈R)，则函数y=f(-x)在其定义域上是（ ）。‎ ‎ A．单调递减的偶函数 B.单调递减的奇函数 ‎ C．单凋递增的偶函数 D．单涮递增的奇函数 ‎2 ‎ ‎2 ‎ 侧(左)视图 ‎ ‎2 ‎ ‎2 ‎ ‎2 ‎ 正(主)视图 ‎ ‎7、一个空间几何体的三视图如图所示,则该几何体的体积为( )。‎ A. B. ‎ C. D. ‎ 俯视图 ‎ ‎8、已知，则的 最小值是（ ）。‎ A．2 B． C．4 D．5‎ ‎9、已知圆：+=1，圆与圆关于直线对称，则圆的方程为（ ）。‎ A．+=1 B．+=1‎ C．+=1 D．+=1‎ ‎10、广州2010年亚运会火炬传递在A、B、C、D、E五个城市之间进行，各城市之间的路线距离（单位：百公里）见右表.若以A为起点，E为终点，每个城市经过且只经过一次，那么火炬传递的最短路线距离是 （ ）。‎ A. B‎.21 C.22 D.23 ‎ ‎（五）‎ ‎1、设集合，则（ ）。‎ ‎ A． B． ‎ C． D．‎ ‎2、下列n的取值中，使=1(i是虚数单位）的是（ ）。‎ A.n=2 B .n=‎3 C .n=4 D .n=5 ‎ ‎3、若向量满足,与的夹角为,则（ ）。‎ ‎ A． B． C. D．2‎ ‎4、的内角A、B、C的对边分别为a、b、c，若，则等于（ ）。‎ A． B．‎2 ‎ C． D．‎ ‎5、若函数，则下列结论正确的是（ ）。‎ A.，在上是增函数 ‎ B.，在上是减函数 C.，是偶函数 D.，是奇函数 ‎（六）‎ ‎6、设是两个不同的平面，是一条直线，以下命题正确的是（ ）。‎ A．若，则 B．若，则 ‎ C．若，则 D．若，则 ‎ ‎7、在实数的原有运算法则中，我们补充定义新运算“”如下：‎ ‎ 当时，； 当时，。‎ ‎ 则函数的最大值等于（ C ）‎ ‎ （“·”和“－”仍为通常的乘法和减法）‎ A. B. ‎1 ‎‎ ‎ C. 6 D. 12‎ ‎8、已知为等差数列，，则等于（ ）。‎ ‎ A. -1 B. ‎1 ‎ C. 3 D.7‎ ‎96 98 100 102 104 106 ‎ ‎0.150 ‎ ‎0.125 ‎ ‎0.100 ‎ ‎0.075 ‎ ‎0.050 ‎ 克 ‎ 频率/组距 ‎ 第8题图 ‎ ‎9、某工厂对一批产品进行了抽样检测.有图是根据抽样检测后的产品净重（单位：克）数据绘制的频率分布直方图，其中产品净重的范围是[96，106]，样本数据分组为[96，98），[98，100),‎ ‎[100，102)，[102，104),[104，106],已知样本中产品净重小于‎100克的个数是36，则样本中净重大于或等于‎98克并且小于‎104克的产品的个数是( )。 ‎ ‎ ‎ A.90 B‎.75 C. 60 D.45‎ ‎10、设，若函数，，有大于零的极值点，则（ ）。‎ A、 B、 C、 D、‎ ‎（七）‎ ‎1、已知全集U=R，则正确表示集合M= {－1，0，1} 和N= { x |x+x=0} 关系的韦恩（Venn）图是（ ）。‎ ‎2、若（为虚数单位），则的值可能是（ ）。‎ ‎ A B C D ‎ ‎3、已知平面向量，，且//，则＝（ ）。‎ A、 B、 C、 D、‎ ‎4、函数的最小值和最大值分别为（ ）。‎ A. －3，1 B. －2，‎2 ‎C. －3， D. －2，‎ ‎1 ‎ x ‎ y ‎ ‎1 ‎ O ‎ A ‎ x ‎ y ‎ O ‎ ‎1 ‎ ‎1 ‎ B ‎ x ‎ y ‎ O ‎ ‎1 ‎ ‎1 ‎ C ‎ x ‎ y ‎ ‎1 ‎ ‎1 ‎ D ‎ O ‎ ‎5、函数的图像大致为( )。 ‎ ‎（八）‎ ‎6、若是互不相同的空间直线，是不重合的平面，则下列命题中为真命题的是（ ）。‎ ‎ ‎ ‎7、已知两个函数和的定义域和值域都是集合{1,2,3},其定义如下表. ‎ x ‎1‎ ‎2‎ ‎3‎ g（x）‎ ‎ 1‎ ‎3‎ ‎2‎ x ‎1‎ ‎2‎ ‎3‎ f（x）‎ ‎ 2‎ ‎3‎ ‎1‎ x ‎1‎ ‎2‎ ‎3‎ g (f（x）)‎ ‎ ‎ 填写下列的表格,其三个数依次为（ ）。‎ A. 3,1,2 B . 2,1,‎3 C. 1,2,3 D. 3,2,1‎ ‎8、不等式组所表示的平面区域的面积等于（ ）。‎ A． B. C. D. ‎ ‎9、某程序框图如图所示，该程序运行后输出的的值是（ ）。‎ A． B． C． D．‎ ‎10、若函数的导函数在区间上是增函数，‎ a b a b a o x o x y b a o x y o x y b 则函数在区间上的图象可能是（ ）。‎ y ‎ A ． B． C． D．‎ ‎（九）‎ ‎1、集合,,若,则的值为( )。‎ A.0 B‎.1 C.2 D.4‎ ‎2、i是虚数单位，i（1+i）等于（ ）。‎ ‎ A.1+i B.－1－i C.1－i D.－1+i学 ‎3、平面向量与的夹角为， ，则( )。 ‎ ‎　 Ａ.　　　　Ｂ.　　 　Ｃ.4　　　　Ｄ.12‎ ‎4、已知简谐运动的图象经过点(0,1),则该简谐运动的最小正周期T 和初相分别为( )。‎ ‎5、若函数是函数的反函数，且，则 （ ）。‎ A． B． C． D．2 ‎ ‎（十）‎ 正视图 侧视图 俯视图 ‎6、如图，一个空间几何体的正视图、侧视图都是面积为，且一个内角为的菱形，俯视图为正方形，那么这个几何体的表面积为（ ）。‎ A. B.‎ ‎ C . 4 D. 8‎ ‎7、定义运算x※y=，若|m－1|※m=|m－1|，则m的取值范围是（ ）。 ‎ A． B． ‎ C． D．‎ ‎8、直线与圆的位置关系为（ ）。‎ A．相切 B．相交但直线不过圆心 ‎ C．直线过圆心 D．相离 ‎9、一个容量100的样本，其数据的分组与各组的频数如下表 组别 频数 ‎12‎ ‎13‎ ‎24‎ ‎15‎ ‎16‎ ‎13‎ ‎7‎ 则样本数据落在上的频率为（ ）。‎ A. 0.13‎‎ B. ‎0.39 ‎‎ C. 0.52 D. 0.64‎ ‎10、函数的单调递增区间是（ ）。‎ A. B.(0,3) C.(1,4) D. w.w.w.k.s.5.u.c.o.m ‎ ‎（十一）‎ ‎1、第二十九届夏季奥林匹克运动会将于‎2008年8月8日在北京举行，若集合A={参加北京奥运会比赛的运动员}，集合B={参加北京奥运会比赛的男运动员}。集合C={参加北京奥运会比赛的女运动员}，则下列关系正确的是（ ）。‎ A.AB      B.BC C.A∩B=C D.B∪C=A ‎2、是虚数单位，=（ ）。‎ A B C D ‎ ‎3、已知向量，．若向量满足，，则（ ）。‎ A． B． C． D．‎ ‎4、已知中，的对边分别为a,b,c若a=c=且，则b=（ ）。‎ A.2 B．4＋ C．4— D．‎ ‎5、如图所示，一质点在平面上沿曲线运动，速度大小不变，其在轴上的投影点的运动速度的图象大致为 （ ）。‎ A B C D ‎（十二）‎ ‎2‎ 俯视图 主视图 左视图 ‎2‎ ‎1‎ ‎2‎ ‎6、如果一个几何体的三视图如图所示(单位长度: cm), 则此几何体的表面积是（ ）。‎ ‎ A. B‎.21 cm ‎ C. D. ‎24 cm ‎ ‎7、对任意实数，定义运算 ‎，其中为常数，等号右边的运算是通常意义的加、乘运算。现已知，且有一个非零实数，使得对任意实数，都有，则( ) 。‎ A. 5 B‎.15 C. 20 D. 10 ‎ ‎8、经过圆的圆心C，且与直线垂直的直线方程是（ ）。‎ A、 B、 ‎ ‎ C、 D、‎ ‎9、公差不为零的等差数列的前项和为.若是的等比中项, ,则等于（ ）。‎ A. 18 B. ‎24 ‎‎ C. 60 D. 90‎ ‎10、阅读右面的程序框图，则输出的S=（ ）。‎ A .14 B. ‎20 C.30 D. 55‎ ‎（十三）‎ ‎1、已知集合,,则=（ ）。‎ ‎ A．{x|-1≤x＜1} B．{x |x>1} C．{x|-1＜x＜1} D．{x |x≥-1}‎ ‎2、已知复数，那么＝（ ）。‎ A. B. C. D.‎ ‎3、已知平面向量=（1，－3），=（4，－2），与垂直，则是（ ）。‎ A. －1 B. ‎1 ‎ C. －2 D. 2‎ ‎4、已知函数，则是（ ）。‎ A、最小正周期为的奇函数 B、最小正周期为的奇函数 C、最小正周期为的偶函数 D、最小正周期为的偶函数 ‎5、定义在R上的函数f(x)满足f(x)= ，则f（3）的值为（ ）。‎ A.-1 B. ‎-2 C.1 D. 2‎ ‎（十四）‎ ‎6、如下图，某几何体的正视图与侧视图都是边长为1的正方形，且体积为。则该集合体的俯视图可以是（ ）。‎ ‎7、定义运算 ，若复数，，则（ ）。‎ ‎ A. 4 B. ‎-4 C. 8 D.-8 ‎ ‎8、已知等比数列的公比为正数，且·=2，=1，则=（ ）。‎ A. B. C. D.2 ‎ ‎9、某单位共有老、中、青职工430人,其中青年职工160人，中年职工人数是老年职工人数的2倍。为了解职工身体状况，现采用分层抽样方法进行调查，在抽取的样本中有青年职工32人，则该样本中的老年职工人数为（ ） ‎ A.9 B.18 C.27 D.36‎ ‎10、图l是某县参加2007年高考的学 生身高条形统计图，从左到右的各条形表示的学生人数依次记为4，、A：、…、A，。(如A：表示身高(单位：cm)在[150，155)内的学生人数)．图2是统计图l中身高在一定范围内学生人数的一个算法流程图．现要统计身高在160～‎180cm(含‎160cm，不含‎180cm)的学生人数，那么在流程图中的判断框内应填写的条件是（ ）。‎ A.i<9 B.i<8 ‎ C.i<7 D.i<6‎ ‎（十五）‎ ‎1、已知集合M＝﹛x|－3＜x5﹜,N＝﹛x|x＜－5或x＞5﹜，则MN＝ ‎ ‎（ ）。‎ A.﹛x|x＜－5或x＞－3﹜ B.﹛x|－5＜x＜5﹜‎ C.﹛x|－3＜x＜5﹜ D.﹛x|x＜－3或x＞5﹜‎ ‎2、若复数(1+bi)(2+i)是纯虚数(i是虚数单位，b是实数)，则b=（ ）。‎ A．-2 B． C. D．2‎ ‎3、设平面向量，则（ ）。‎ ‎　 A.　　 　B.　　 C.　 　D.‎ ‎4、函数的图象是（ ）。‎ ‎5、命题“若函数在其定义域内是减函数，则”的逆否命题是（ ）。‎ A、若，则函数在其定义域内不是减函数 B、若，则函数在其定义域内不是减函数 C、若，则函数在其定义域内是减函数 D、若，则函数在其定义域内是减函数 ‎（十六）‎ ‎6、给定下列四个命题： ‎ ‎①若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行； ‎ ‎②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直； ‎ ‎③垂直于同一直线的两条直线相互平行；w.w.w.k.s.5.u.c.o.m ‎ ‎④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直. ‎ 其中，为真命题的是（ ）。‎ A．①和② B．②和③ C．③和④ D．②和④ ‎ ‎7、在R上定义运算△：x△y=x(1 -y) 若不等式(x-a)△(x+a)<1,对任意实数x恒成立，则实数a的取值范围是（ ）。‎ A． B． C． D．‎ ‎8、设则（ ）。‎ A. B. C. D.‎ ‎9、在一个袋子中装有分别标注数字1，2，3，4，5的五个小球，这些小球除标注的数字外完全相同．现从中随机取出2个小球，则取出的小球标注的数字之和为3或6的概率是（ ）。‎ ‎10、设函数，其中，则导数的取值范围是（ ）。‎ ‎ A. B. C. D. ‎ ‎（十七）‎ ‎1、设集合＝｛｜ ｝，＝｛｜｝.则＝（ ）。‎ ‎ A.｛｜－7＜＜－5 ｝ B.｛｜ 3＜＜5 ｝‎ C.｛｜ －5 ＜＜3｝ D.｛｜ －7＜＜5 ｝ ‎ ‎2、已知0＜a＜2，复数(i是虚数单位)，则|z|的取值范围是（ ）。‎ A.(1,) B. (1,) C.(1,3) D.(1,5)‎ ‎3、若，, 则（ ）。‎ A．（1，1） B．（－1，－1） C．（3，7） D．（-3,-7） ‎ ‎4、函数是（ ）。‎ A．最小正周期为的奇函数 B. 最小正周期为的偶函数 ‎ C. 最小正周期为的奇函数 D. 最小正周期为的偶函数 ‎ ‎5、设，函数的图像可能是（ ）。‎ ‎（十八）‎ ‎6、若正方体的棱长为，则以该正方体各个面的中心为顶点的凸多面体的体积为（ ）。‎ A. B. C. D. ‎ ‎7、直角坐标系中横坐标、纵坐标均为整数的点称为格点，如果函数f(x)的图象恰好通过k(k∈N*)个格点，则称函数f(x)为k阶格点函数。下列函数：‎ ① f(x)=sinx； ②f(x)=π(x－1)2+3； ③ ④，‎ 其中是一阶格点函数的有（ ）。 ‎ A、①④ B、①②④ C、①②③ D、②③‎ ‎8、设，若，则下列不等式中正确的是（ ）。‎ 是 否 开始 输入a,b,c x=a b>x 输出x 结束 x=b x=c 否 是 A、 B、 C、 D、9、双曲线-=1的焦点到渐近线的距离为（ ）。‎ A. B‎.2 C. D.1‎ ‎10、下面的程序框图，如果输入三个实数a、b、c，要求输出这三个数中最大的数，那么在空白的判断框中，应该填入下面四个选项中的（ ）。‎ A. c > x B. x > c C. c > b D. b > c ‎（十九）‎ ‎1、已知全集U=R，则正确表示集合M= {－1，0，1} 和N= { x |x+x=0} 关系的韦恩（Venn）图是（ ）。‎ ‎2、若（为虚数单位），则的值可能是（ ）。‎ ‎ A B C D ‎ ‎3、已知平面向量，，且//，则＝（ ）。‎ A、 B、 C、 D、‎ ‎4、函数的最小值和最大值分别为（ ）。‎ A. －3，1 B. －2，‎2 ‎C. －3， D. －2，‎ ‎1 ‎ x ‎ y ‎ ‎1 ‎ O ‎ A ‎ x ‎ y ‎ O ‎ ‎1 ‎ ‎1 ‎ B ‎ x ‎ y ‎ O ‎ ‎1 ‎ ‎1 ‎ C ‎ x ‎ y ‎ ‎1 ‎ ‎1 ‎ D ‎ O ‎ ‎5、函数的图像大致为( )。 ‎ ‎（二十）‎ ‎6、若是互不相同的空间直线，是不重合的平面，则下列命题中为真命题的是（ ）。‎ ‎ ‎ ‎7、已知两个函数和的定义域和值域都是集合{1,2,3},其定义如下表. ‎ x ‎1‎ ‎2‎ ‎3‎ f（x）‎ ‎ 2‎ ‎3‎ ‎1‎ x ‎1‎ ‎2‎ ‎3‎ g（x）‎ ‎ 1‎ ‎3‎ ‎2‎ x ‎1‎ ‎2‎ ‎3‎ g (f（x）)‎ ‎ ‎ 填写下列的表格,其三个数依次为（ ）。‎ A. 3,1,2 B . 2,1,‎3 C. 1,2,3 D. 3,2,1‎ ‎8、不等式组所表示的平面区域的面积等于（ ）。A． B. C. D. ‎ ‎9、某程序框图如图所示，该程序运行后输出的的值是（ ）。‎ A． B． C． D．‎ ‎10、若函数的导函数在区间上是增函数，‎ 则函数在区间上的图象可能是（ ）。‎ y a b a b a o x o x y b a o x y o x y b ‎ A ． B． C． D．‎ ‎（二十一）‎ ‎1、集合,,若,则的值为( )。‎ A.0 B‎.1 C.2 D.4‎ ‎2、i是虚数单位，i（1+i）等于（ ）。‎ ‎ A.1+i B.－1－i C.1－i D.－1+i学 ‎3、平面向量与的夹角为， ，则( )。 ‎ ‎　 Ａ.　　　　Ｂ.　　 　Ｃ.4　　　　Ｄ.12‎ ‎4、已知简谐运动的图象经过点(0,1),则该简谐运动的最小正周期T 和初相分别为( )。‎ ‎5、若函数是函数的反函数，且，则 （ ）。‎ A． B． C． D．2 ‎ ‎（二十二）‎ 正视图 侧视图 俯视图 ‎6、如图，一个空间几何体的正视图、侧视图都是面积为，且一个内角为的菱形，俯视图为正方形，那么这个几何体的表面积为（ ）。‎ A. B.‎ ‎ C . 4 D. 8‎ ‎7、定义运算x※y=，若|m－1|※m=|m－1|，则m的取值范围是（ ）。 ‎ A． B． ‎ C． D．‎ ‎8、直线与圆的位置关系为（ ）。‎ A．相切 B．相交但直线不过圆心 ‎ C．直线过圆心 D．相离 ‎9、一个容量100的样本，其数据的分组与各组的频数如下表 组别 频数 ‎12‎ ‎13‎ ‎24‎ ‎15‎ ‎16‎ ‎13‎ ‎7‎ 则样本数据落在上的频率为（ ）。‎ A. 0.13‎‎ B. ‎0.39 ‎‎ C. 0.52 D. 0.64‎ ‎10、函数的单调递增区间是（ ）。‎ A. B.(0,3) C.(1,4) D. w.w.w.k.s.5.u.c.o.m ‎ 高三数学专题复习：选择题训练（一）‎ ‎（ 训练时间：40分钟 总分：50分）‎ 参 考 答 案 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 B D C A B B C C B B 解 析 ‎1、集合；对于，因此．答案 B ‎2、复数； 可设，由得 ‎【答案】:D．‎ ‎3、平面向量； ,由及向量的性质可知, C正确.‎ ‎4、三角函数；答案 A ‎5、数列；, 选B.‎ ‎6、函数； 函数单调递减且为奇函数,选(B).‎ ‎7、立体几何； 该空间几何体为一圆柱和一四棱锥组成的,圆柱的底面半径为1,高为2,体积为,四棱锥的底面边长为，高为，所以体积为 所以该几何体的体积为.答案:C ‎8、不等式； 因为当且仅当，且 ，即时，取“=”号。答案 C ‎9、解析几何。设圆的圆心为（a，b），则依题意，有，解得：，对称圆的半径不变，为1，故选B。.‎ ‎10、新信息题；.由题意知,所有可能路线有6种：‎ ‎①,②,③,④,⑤,⑥, ‎ 其中, 路线③的距离最短, 最短路线距离等于, 故选B.‎ 高三数学专题复习：选择题训练（二）‎ ‎（ 训练时间：40分钟 总分：50分）‎ 参 考 答 案 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 A C B D C C C B A A 解 析 ‎1、集合； 本题主要考查集合的基本运算以及简单的不等式的解法. 属于基础知识、基本运算的考查∵，‎ ‎∴，故选A.‎ ‎2、复数； 因为, 故选C. ‎ ‎3、平面向量；, 选(B).‎ ‎4、三角函数；【答案】D ‎5、函数； 对于时有是一个偶函数，答案 C ‎6、立体几何； 对于A、B、D均可能出现，而对于C是正确的． ‎ ‎7、新信息题；【答案】C ‎8、数列；∵即∴‎ 同理可得∴公差∴. 选B。‎ ‎9、概率与统计；产品净重小于‎100克的概率为(0.050+0.100)×2=0.300, ‎ 已知样本中产品净重小于‎100克的个数是36,设样本容量为,‎ 则,所以,净重大于或等于‎98克并且小于 ‎104克的产品的概率为(0.100+0.150+0.125)×2=0.75,所以样本 中净重大于或等于‎98克并且小于‎104克的产品的个数是 ‎120×0.75=90.故选A.‎ ‎10、导数；题意即有大于0的实根,数形结合令,则两曲线交点在第一象限,结合图像易得,选A.‎ 高三数学专题复习：选择题训练（三）‎ ‎（ 训练时间：40分钟 总分：50分）‎ 参 考 答 案 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 B D B C A D D C A A 解 析 ‎1、集合； 由N= { x |x+x=0}得,选B.‎ ‎2、复数；：把代入验证即得。【答案】 D ‎3、平面向量； 排除法:横坐标为, 选B.‎ ‎4、三角函数； ∵ ‎ ‎∴当时，，当时，；故选Ｃ；‎ ‎5、函数； 函数有意义,需使,其定义域为,排除C,D,又因为,所以当时函数为减函数,故选A. ‎ ‎6、立体几何； 逐一判除,易得答案(D).‎ ‎7、新信息题；答案：D ‎8、不等式；A B C x y O 不等式表示的平面区域如图所示阴影部分△ABC 由得A（1，1），又B（0，4），C（0，）‎ ‎∴S△ABC=，选C。‎ ‎9、算法；对于，而对于，则，后面是，不符合条件时输出的．A ‎10、导数。因为函数的导函数在区间上是增函数，即在区间上各点处的斜率是递增的，由图易知选A. 注意C中为常数噢.‎ 高三数学专题复习：选择题训练（四）‎ ‎（ 训练时间：40分钟 总分：50分）‎ 参考答案 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 D D B A A C D B C D 解 析 ‎1、集合； 解析 ∵,,∴∴, 故选D.‎ ‎2、复数； ， 选D ‎3、平面向量； ，，，‎ ‎，。选B ‎4、三角函数；依题意,结合可得,易得,故选(A).‎ ‎5、函数；函数的反函数是,又,即, 所以,,故,选A.‎ ‎6、立体几何；答案 C。 7、新信息题；答案 D 。‎ ‎8、解析几何；圆心为到直线，即的距离，而，选B。‎ ‎9、概率与统计；由题意可知频数在的有：13+24+15=52，由频率=频数总数可得0.52. 故选C.‎ ‎10、导数。,令,解得,故选D