阿基米德三角形性质与高考题 4页

阿基米德三角形性质与高考题 性质1：阿基米德三角形底边上的中线平行于抛物线的轴 即：‎ A B C P Q O x y l ‎19．（07年江苏卷）如图，在平面直角坐标系中，过轴正方向上一点任作一直线，与抛物线相交于两点．一条垂直于轴的直线，分别与线段和直线交于点．‎ ‎（1）若，求的值；（5分）‎ ‎（2）若为线段的中点，求证：为此抛物线的切线；（5分）‎ ‎（3）试问（2）的逆命题是否成立？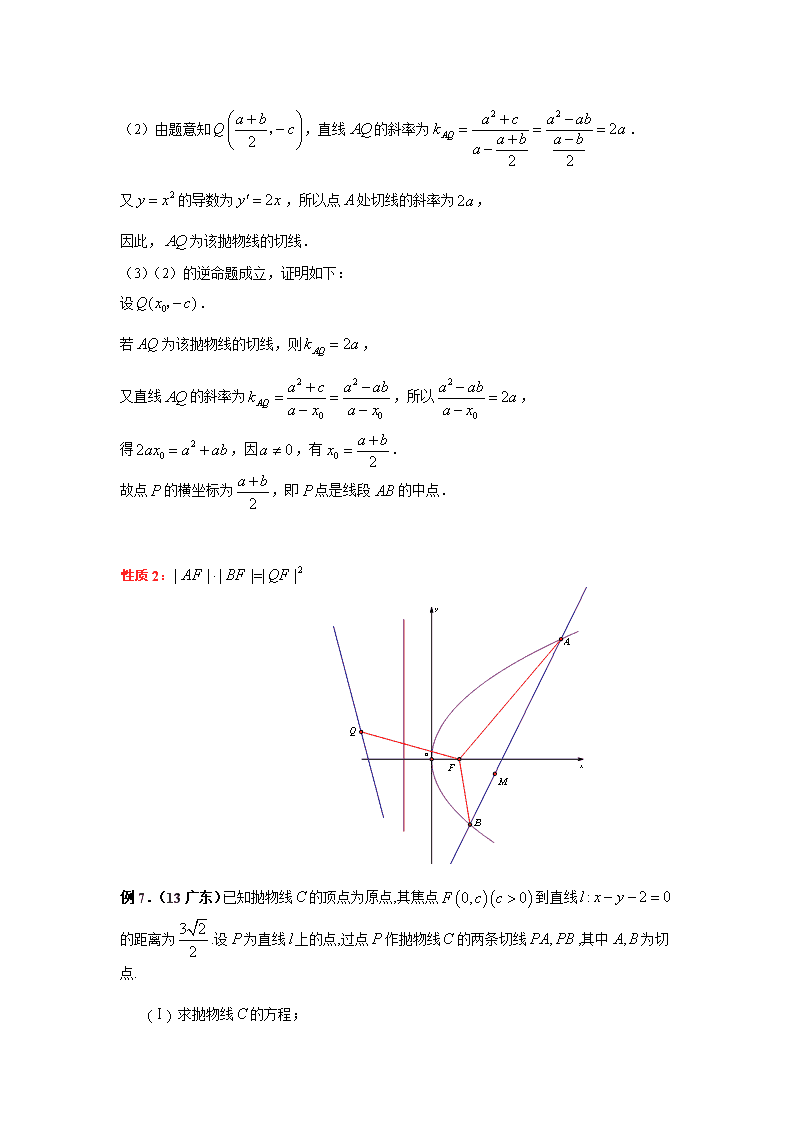说明理由．（4分）‎ ‎19．本小题主要考查抛物线的基本性质、直线与抛物线的位置关系、向量的数量积、导数的应用、简易逻辑等基础知识和基本运算，考查分析问题、探索问题的能力．满分14分．‎ A B C P Q O x y l 解：（1）设直线的方程为，‎ 将该方程代入得．‎ 令，，则．‎ 因为，解得，‎ 或（舍去）．故．‎ ‎（2）由题意知，直线的斜率为．‎ 又的导数为，所以点处切线的斜率为，‎ 因此，为该抛物线的切线．‎ ‎（3）（2）的逆命题成立，证明如下：‎ 设．‎ 若为该抛物线的切线，则，‎ 又直线的斜率为，所以，‎ 得，因，有．‎ 故点的横坐标为，即点是线段的中点．‎ 性质2：‎ 例7．（13广东）已知抛物线的顶点为原点,其焦点到直线:的距离为.设为直线上的点,过点作抛物线的两条切线,其中为切点.‎ ‎(Ⅰ) 求抛物线的方程；‎ ‎(Ⅱ) 当点为直线上的定点时,求直线的方程；‎ ‎(Ⅲ) 当点在直线上移动时,求的最小值.‎ 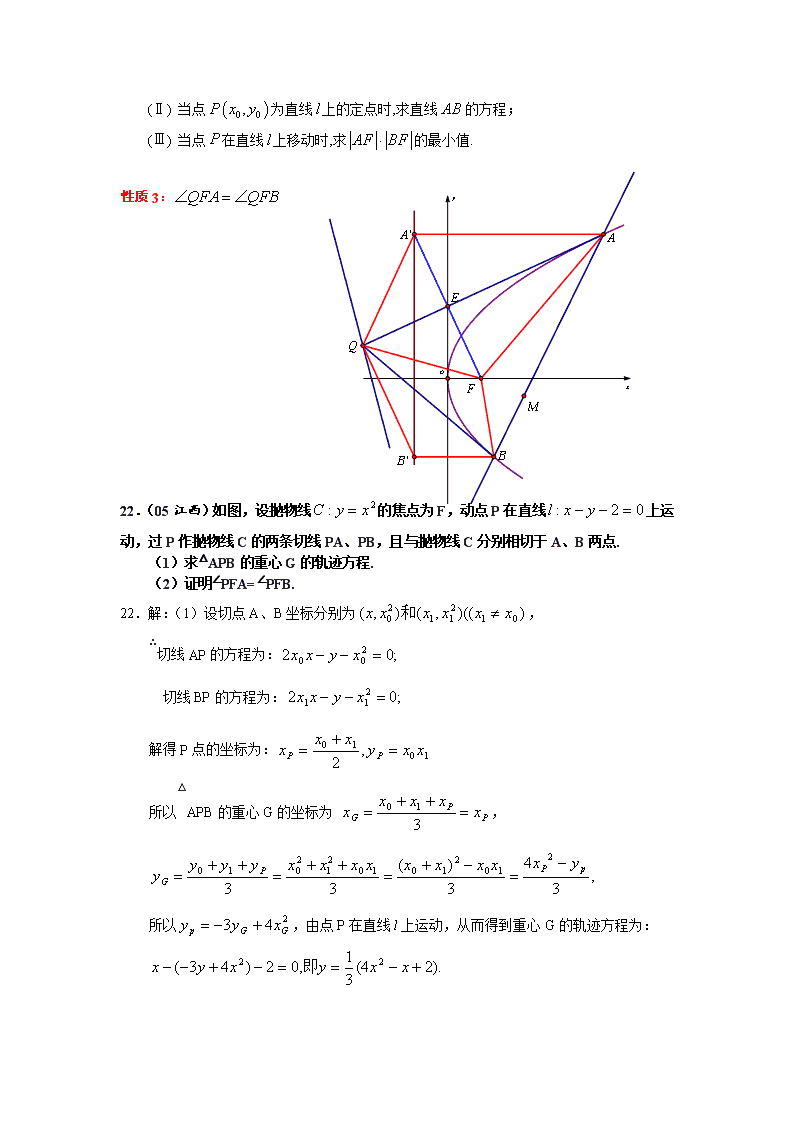性质3：‎ ‎22．（05江西）如图，设抛物线的焦点为F，动点P在直线上运动，过P作抛物线C的两条切线PA、PB，且与抛物线C分别相切于A、B两点.‎ ‎（1）求△APB的重心G的轨迹方程.‎ ‎（2）证明∠PFA=∠PFB.‎ ‎22．解：（1）设切点A、B坐标分别为，‎ ‎∴切线AP的方程为：‎ ‎ 切线BP的方程为：‎ 解得P点的坐标为：‎ 所以△APB的重心G的坐标为 ，‎ 所以，由点P在直线l上运动，从而得到重心G的轨迹方程为：‎ ‎ （2）因为 由于P点在抛物线外，则 ‎∴‎ 同理有 ‎∴∠AFP=∠PFB.‎ 性质4：过焦点的阿基米德三角形面积的最小值为 ‎（21）（06年全国卷2）已知抛物线的焦点为F，A、B是热线上的两动点，且过A、B两点分别作抛物线的切线，设其交点为M。‎ ‎（I）证明为定值；‎ ‎（II）设的面积为S，写出的表达式，并求S的最小值。‎