一轮特效提高2014高考总复习理数题库112统计图表数据的数字特征用样本估计总体 13页

‎11.2 统计图表、数据的数字特征、用样本估计总体 一、选择题 ‎1．从一堆苹果中任取10只，称得它们的质量如下(单位：克)：125,120,122,105,130,114,116,95,120,134，‎ 则样本数据落在[114.5,124.5)内的频率为(　　)．‎ A．0.2 B．0.3 C．0.4 D．0.5‎ 解析　数据落在[114.5,124.5)内的有：120,122,116,120共4个，故所求频率为＝0.4.[来源:Z_xx_k.Com]‎ 答案　C ‎2．样本中共有五个个体，其值分别为a,0,1,2,3.若该样本的平均值为1，则样本方差为(　　)．‎ A. B. C. D．2‎ 解析　由题可知样本的平均值为1，所以＝1，解得a＝－1，所以样本的方差为[(－1－1)2＋(0－1)2＋(1－1)2＋(2－1)2＋(3－1)2]＝2.‎ 答案　D ‎3某班50名学生在一次百米测试中，成绩全部在[13,18]内，将测试结果按如下方式分成五组：第一组[13,14)；第二组[14,15)；…；第五组[17,18]．如图是按上述分组方法得到的频率分布直方图．且第一组，第二组，第四组的频数成等比数列，则成绩在[13,15)内的学生人数为(　　)‎ A．12 B．14‎ C．16 D．10‎ 解析 由图知第一、三、五小组的频率分别为0.08,0.38,0.06，‎ ‎∴其频数分别为4,19,3，‎ ‎∴第二、四组的频数和为50－4－19－3＝24.‎ ‎∵第一、二、四组的频数成等比数列，设其公比为q，则第二、四组的频数为4q,4q2.‎ ‎∴4q＋4q2＝24，解得q＝2或q＝－3(舍去)，‎ ‎∴第二小组的频数为4q＝8，‎ ‎∴成绩在[13,15)内的学生有4＋8＝12(人)．‎ 答案 A ‎4.有一个容量为200的样本，其频率分布直方图如图所示．根据样本的频率分布直方图估计，样本数据落在区间[10,12)内的频数为(　　)‎ A．18 B．36 C．54 D．72‎ 答案 B 解析 本题考查频率分布直方图．做这类题应注意组距、各小矩形的面积和为1等．1－2(0.02＋0.05＋0.15＋0.19)＝0.18，‎ 所以0.18×200＝36.‎ ‎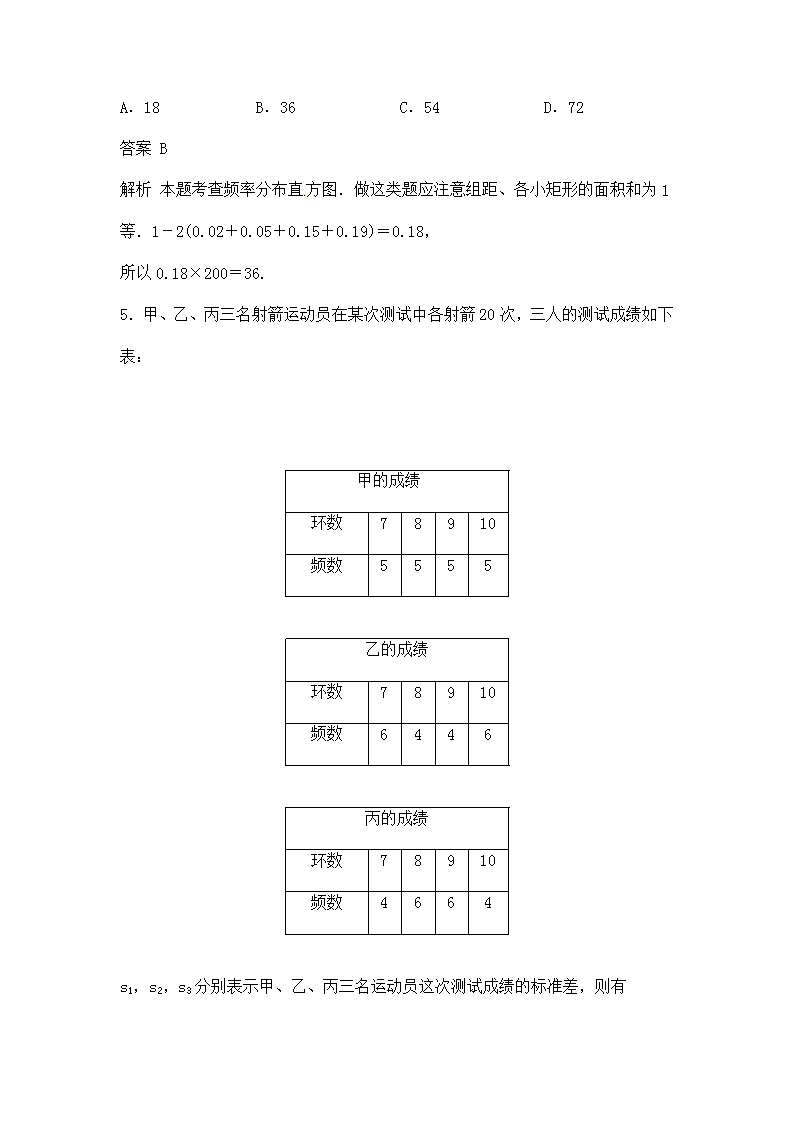5．甲、乙、丙三名射箭运动员在某次测试中各射箭20次，三人的测试成绩如下表：‎ 甲的成绩[来源:学科网]‎ 环数 ‎7‎ ‎8‎ ‎9‎ ‎10‎ 频数 ‎5‎ ‎5‎ ‎5‎ ‎5‎ 乙的成绩 环数 ‎7‎ ‎8‎ ‎9‎ ‎10‎ 频数 ‎6‎ ‎4‎ ‎4‎ ‎6‎ 丙的成绩 环数 ‎7‎ ‎8‎ ‎9‎ ‎10‎ 频数 ‎4‎ ‎6‎ ‎6‎ ‎4‎ s1，s2，s3分别表示甲、乙、丙三名运动员这次测试成绩的标准差，则有 ‎(　　)．‎ A．s3＞s1＞s2 B．s2＞s1＞s3‎ C．s1＞s2＞s3 D．s2＞s3＞s1‎ 解析　∵甲＝＝8.5，‎ s＝ ‎＝1.25，乙＝＝8.5，‎ s＝ ‎＝1.45，丙＝＝8.5，‎ s＝ ‎＝1.05.由s＞s＞s，得s2＞s1＞s3.‎ 答案　B ‎6．对某种电子元件的使用寿命进行跟踪调查，所得样本的频率分布直方图如图所示，由图可知，这一批电子元件中使用寿命在100～300 h的电子元件的数量与使用寿命在300～600 h的电子元件的数量的比是(　　)．‎ A. B. C. D. 解析　寿命在100～300 h的电子元件的频率为 ×100＝＝；‎ 寿命在300～600 h的电子元件的频率为 ×100＝.‎ ‎∴它们的电子元件数量之比为∶＝.‎ 答案　C ‎7．一组数据的平均数是2.8，方差是3.6，若将这组数据中的每一个数据都加上60，得到一组新数据，则所得新数据的平均数和方差分别是(　　)．‎ A．57.2,3.6 B．57.2,56.4 C．62.8,63.6 D．62.8,3.6‎ 解析　平均数增加，方差不变．‎ 答案　D 二、填空题 ‎8．某企业3个分厂生产同一种电子产品，第一、二、三分厂的产量之比为1∶2∶1，用分层抽样方法(每个分厂的产品为一层)从3个分厂生产的电子产品中共抽取100件作使用寿命的测试，由所得的测试结果算得从第一、二、三分厂取出的产品的使用寿命的平均值分别为980 h,1 020 h,1 032 h，则抽取的100件产品的使用寿命的平均值为________h.‎ 解析 由于三个厂的产量比为1∶2∶1，‎ 所以从三个厂抽出产品比例也应为1∶2∶1.‎ 所以100件产品的使用寿命平均值为＝1 013.‎ 答案 1 013‎ ‎9一个样本a,99，b,101，c中，五个数顺次成等差数列，则这个样本的标准差为________．‎ 答案 解析 ∵a,99，b,101，c成等差数列，‎ ‎∴b＝＝100，‎ ‎∴a＝98，c＝102.‎ ‎∴＝＝100，‎ ‎∴s＝＝.‎ ‎10．某中学为了解学生数学课程的学习情况，在3 000名学生中随机抽取200名，并统计这200名学生的某次数学考试成绩，得到了样本的频率分布直方图(如图)．根据频率分布直方图推测，这3 000名学生在该次数学考试中成绩小于60分的学生数是________．‎ 解析　根据样本的频率分布直方图，成绩小于60分的学生的频率为(0.002＋0.006＋0.012)×10＝0.20，所以可推测3 000名学生中成绩小于60分的人数为600名．‎ 答案　600‎ ‎11‎ ‎．某校开展“爱我青岛，爱我家乡”摄影比赛，9位评委为参赛作品A给出的分数如茎叶图所示．记分员在去掉一个最高分和一个最低分后，算得平均分为91，复核员在复核时，发现有一个数字(茎叶图中的x)无法看清，若记分员计算无误，则数字x应该是________．‎ 解析　当x≥4时，＝≠91，∴x＜4，‎ 则＝91，∴x＝1.‎ 答案　1‎ ‎12．某人5次上班途中所花的时间(单位：分钟)分别为x，y,10,11,9.已知这组数据的平均数为10，方差为2，则x2＋y2的值为________．‎ 解析　由(x＋y＋10＋11＋9)＝10，[(x－10)2＋(y－10)2＋0＋1＋1]＝2，联立解得，x2＋y2＝208.‎ 答案　208‎ 三、解答题 ‎13．某种产品的质量以其质量指标值衡量，质量指标值越大表明质量越好，且质量指标值大于或等于102的产品为优质品．现用两种新配方(分别称为A配方和B配方)做试验，各生产了100件这种产品，并测量了每件产品的质量指标值，得到下面试验结果：‎ A配方的频数分布表 指标值 分组 ‎[90,94)‎ ‎[94,98)‎ ‎[98,102)‎ ‎[102,106)‎ ‎[106,110]‎ 频数 ‎8‎ ‎20‎ ‎42‎ ‎22‎ ‎8‎ B配方的频数分布表 指标值 分组 ‎[90,94)‎ ‎[94,98)‎ ‎[98,102)‎ ‎[102,106)‎ ‎[106,110][来源:学|科|网]‎ 频数 ‎4‎ ‎12‎ ‎42‎ ‎32[来源:学科网]‎ ‎10‎ ‎(1)分别估计用A配方，B配方生产的产品的优质品率；‎ ‎(2)已知用B配方生产的一件产品的利润y(单位：元)与其质量指标值t的关系式为y＝ 估计用B配方生产的一件产品的利润大于0的概率，并求用B配方生产的上述100件产品平均一件的利润．‎ 解析　(1)由试验结果知，用A配方生产的产品中优质品的频率为＝0.3，所以用A配方生产的产品的优质品率的估计值为0.3.‎ 由试验结果知，用B配方生产的产品中优质品的频率为＝0.42，所以用B配方生产的产品的优质品率的估计值为0.42.‎ ‎(2)由条件知，用B配方生产的一件产品的利润大于0当且仅当其质量指标值t≥94，由试验结果知，质量指标值t≥94的频率为0.96.所以用B配方生产的一件产品的利润大于0的概率估计值为0.96.‎ 用B配方生产的产品平均一件的利润为 ×[4×(－2)＋54×2＋42×4]＝2.68(元)．‎ ‎14.中学高三年级参加市一轮验收考试的同学有1 000人，用系统抽样法抽取了一个容量为200的学生总成绩的样本，分数段及各分数段人数如下(满分750分)：‎ 分数段 ‎[250,350)‎ ‎[350,450)‎ ‎[450,550)‎ ‎[550,650)‎ ‎[650,750)‎ 人数 ‎20‎ ‎30‎ ‎80‎ ‎40‎ ‎30‎ ‎(1)列出频率分布表；‎ ‎(2)画出频率分布直方图；‎ ‎(3)模拟本科划线成绩为550分，试估计该校的上线人数．‎ 解析 (1)频率分布表如下：‎ 分数段(分)‎ 频数 频率 ‎[250,350)‎ ‎20‎ ‎0.10‎ ‎[350,450)‎ ‎30‎ ‎0.15‎ ‎[450,550)‎ ‎80‎ ‎0.40‎ ‎[550,650)‎ ‎40‎ ‎0.20‎ ‎[650,750)‎ ‎30‎ ‎0.15‎ 合计 ‎200‎ ‎1.00‎ ‎(2)频率分布直方图如下：‎ ‎(3)由频率分布表知，在样本中成绩在550分以上的人数的频率为 ‎0.20＋0.15＝0.35.‎ 由此可以估计该校本科模拟上线人数约为 ‎0．35×1 000＝350(人)．‎ ‎15．某制造商3月生产了一批乒乓球，随机抽取100个进行检查，测得每个球的直径(单位：mm)，将数据进行分组，得到如下频率分布表：‎ 分组 频数 频率 ‎[39.95,39.97)‎ ‎10‎ ‎[39.97,39.99)‎ ‎20‎ ‎[39.99,40.01)‎ ‎50‎ ‎[40.01,40.03]‎ ‎20‎ 合计 ‎100‎ ‎(1)补充完成频率分布表(结果保留两位小数)，并在上图中画出频率分布直方图；‎ ‎(2)若以上述频率作为概率，已知标准乒乓球的直径为‎40.00 mm，试求这批乒乓球的直径误差不超过‎0.03 mm的概率；‎ ‎(3)统计方法中，同一组数据常用该组区间的中点值(例如区间[39.99,40.01)的中点值是40.00)作为代表．据此估计这批乒乓球直径的平均值(结果保留两位小数)．‎ 解析　(1)频率分布表如下：‎ 分组[来源:学§科§网]‎ 频数 频率 ‎[39.95,39.97)‎ ‎10‎ ‎0.10‎ ‎[39.97,39.99)‎ ‎20‎ ‎0.20‎ ‎[39.99,40.01)‎ ‎50‎ ‎0.50‎ ‎[40.01,40.03]‎ ‎20‎ ‎0.20‎ 合计 ‎100‎ ‎1‎ 频率颁布直方图如图：‎ ‎(2)误差不超过‎0.03 mm，即直径落在[39.97,40.03]内，‎ 其概率为0.2＋0.5＋0.2＝0.9.‎ ‎(3)整体数据的平均值为39.96×0.10＋39.98×0.20＋40.00×0.50＋40.02×0.20＝40.00(mm)．‎ ‎16．某市‎2010年4月1日～‎4月30日对空气污染指数的监测数据如下(主要污染物为可吸入颗粒物)：‎ ‎61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,77,86,81,83,82,82,64,79,86,85,75,71,49,45.‎ 样本频率分布表：‎ 分组 频数 频率 ‎[41,51)‎ ‎2‎ ‎[51,61)‎ ‎1‎ ‎[61,71)‎ ‎4‎ ‎[71,81)‎ ‎6‎ ‎[81,91)‎ ‎10‎ ‎[91,101)‎ ‎[101,111]‎ ‎2‎ ‎(1)完成频率分布表；‎ ‎(2)作出频率分布直方图；‎ ‎(3)根据国家标准，污染指数在0～50之间时，空气质量为优；在51～100之间时，为良；在101～150之间时，为轻微污染；在151～200之间时，为轻度污染．‎ 请你依据所给数据和上述标准，对该市的空气质量给出一个简短评价．‎ 解析　(1)频率分布表：‎ 分组 频数 频率 ‎[41,51)‎ ‎2‎ ‎[51,61)‎ ‎1‎ ‎[61,71)‎ ‎4‎ ‎[71,81)‎ ‎6‎ ‎[81,91)‎ ‎10‎ ‎[91,101)‎ ‎5‎ ‎[101,111]‎ ‎2‎ ‎(2)频率分布直方图：‎ ‎(3)答对下述两条中的一条即可：‎ ‎①该市一个月中空气污染指数有2天处于优的水平，占当月天数的.有26天处于良的水平，占当月天数的.处于优或良的天数共有28天，占当有月数的.说明该市空气质量基本良好．‎ ‎②轻微污染有2天，占当月天数的.污染指数在80以上接近轻微污染的天数有15天，加上处于轻微污染的天数，共有17天，占当月天数的，超过50%.说明该市空气质量有待进一步改善．‎