高考物理第一轮复习22力的合成和分解附练习题及答案1 7页

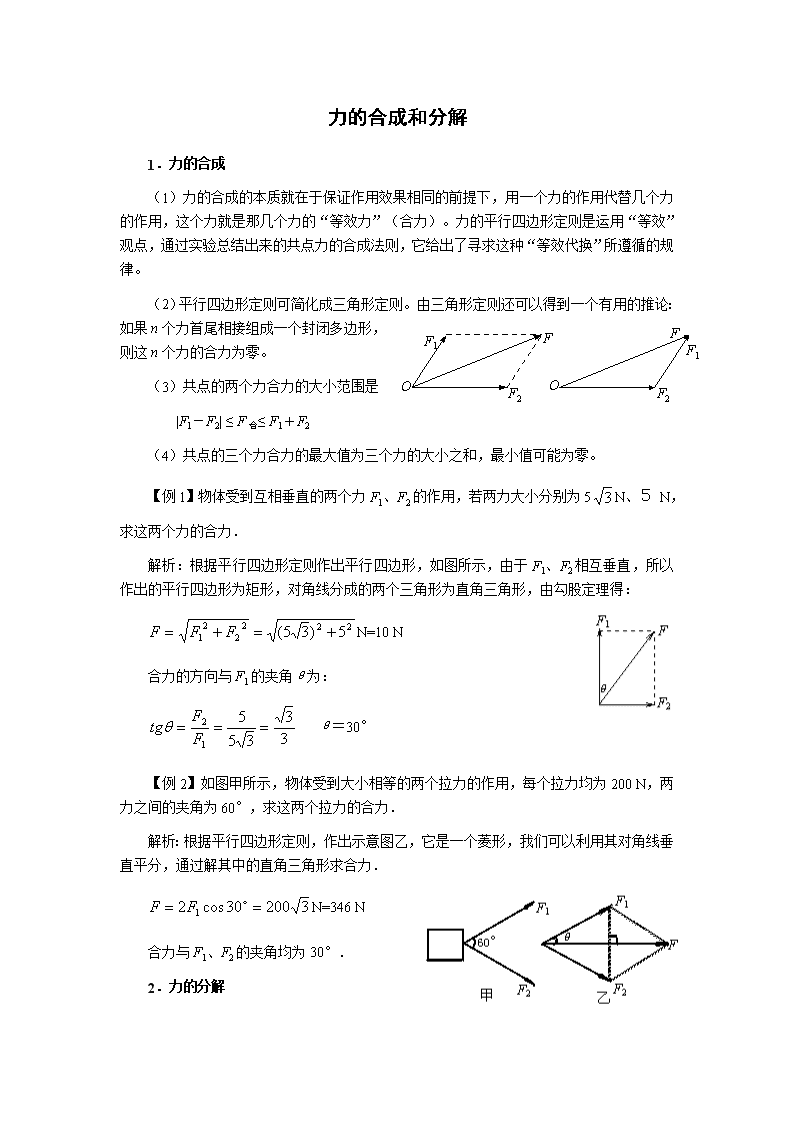
力的合成和分解 ‎1．力的合成 ‎（1）力的合成的本质就在于保证作用效果相同的前提下，用一个力的作用代替几个力的作用，这个力就是那几个力的“等效力”（合力）。力的平行四边形定则是运用“等效”观点，通过实验总结出来的共点力的合成法则，它给出了寻求这种“等效代换”所遵循的规律。‎ F1‎ F2‎ F O F1‎ F2‎ F O ‎（2）平行四边形定则可简化成三角形定则。由三角形定则还可以得到一个有用的推论：如果n个力首尾相接组成一个封闭多边形，则这n个力的合力为零。‎ ‎（3）共点的两个力合力的大小范围是 ‎ |F1－F2| ≤ F合≤ F1＋F2‎ ‎（4）共点的三个力合力的最大值为三个力的大小之和，最小值可能为零。‎ ‎【例1】物体受到互相垂直的两个力F1、F2的作用，若两力大小分别为5N、５ N，求这两个力的合力．‎ 解析：根据平行四边形定则作出平行四边形，如图所示，由于F1、F2相互垂直，所以作出的平行四边形为矩形，对角线分成的两个三角形为直角三角形，由勾股定理得：‎ N=10 N 合力的方向与F1的夹角θ为：‎ ‎ θ＝30°‎ ‎【例2】如图甲所示，物体受到大小相等的两个拉力的作用，每个拉力均为200 N，两力之间的夹角为60°，求这两个拉力的合力．‎ 解析：根据平行四边形定则，作出示意图乙，它是一个菱形，我们可以利用其对角线垂直平分，通过解其中的直角三角形求合力．‎ N=346 N ‎ 合力与F1、F2的夹角均为30°．‎ ‎2．力的分解 ‎（1）力的分解遵循平行四边形法则，力的分解相当于已知对角线求邻边。‎ ‎（2）两个力的合力惟一确定，一个力的两个分力在无附加条件时，从理论上讲可分解为无数组分力，但在具体问题中，应根据力实际产生的效果来分解。‎ ‎【例3】将放在斜面上质量为m的物体的重力mg分解为下滑力F1和对斜面的压力F2，这种说法正确吗？‎ 解析：将mg分解为下滑力F1这种说法是正确的，但是mg的另一个分力F2不是物体对斜面的压力，而是使物体压紧斜面的力，从力的性质上看，F2是属于重力的分力，而物体对斜面的压力属于弹力，所以这种说法不正确。‎ ‎【例4】将一个力分解为两个互相垂直的力，有几种分法？‎ 解析：有无数种分法，只要在表示这个力的有向线段的一段任意画一条直线，在有向线段的另一端向这条直线做垂线，就是一种方法。如图所示。‎ ‎（3）几种有条件的力的分解 ‎①已知两个分力的方向，求两个分力的大小时，有唯一解。‎ ‎②已知一个分力的大小和方向，求另一个分力的大小和方向时，有唯一解。‎ ‎③已知两个分力的大小，求两个分力的方向时，其分解不惟一。‎ ‎④已知一个分力的大小和另一个分力的方向，求这个分力的方向和另一个分力的大小时，其分解方法可能惟一，也可能不惟一。‎ ‎（4）用力的矢量三角形定则分析力最小值的规律：‎ ‎①当已知合力F的大小、方向及一个分力F1的方向时，另一个分力F2取最小值的条件是两分力垂直。如图所示，F2的最小值为：F2min=F sinα ‎ ‎ ‎②当已知合力F的方向及一个分力F1的大小、方向时，另一个分力F2取最小值的条件是：所求分力F2与合力F垂直，如图所示，F2的最小值为：F2min=F1sinα ‎③当已知合力F的大小及一个分力F1的大小时，另一个分力F2取最小值的条件是：已知大小的分力F1与合力F同方向，F2的最小值为｜F－F1｜‎ ‎（5）正交分解法： 把一个力分解成两个互相垂直的分力，这种分解方法称为正交分解法。‎ 用正交分解法求合力的步骤：‎ ‎①首先建立平面直角坐标系，并确定正方向 ‎②把各个力向x轴、y轴上投影，但应注意的是：与确定的正方向相同的力为正，与确定的正方向相反的为负，这样，就用正、负号表示了被正交分解的力的分力的方向 ‎③求在x轴上的各分力的代数和Fx合和在y轴上的各分力的代数和Fy合 ‎④求合力的大小 ‎ 合力的方向：tanα=（α为合力F与x轴的夹角）‎ ‎【例5】质量为m的木块在推力F作用下，在水平地面上做匀速运动．已知木块与地面间的动摩擦因数为µ，那么木块受到的滑动摩擦力为下列各值的哪个? A．µmg Ｂ．µ（mg+Fsinθ）‎ Ｃ．µ（mg+Fsinθ） Ｄ．Fcosθ ‎ ‎ 解析：木块匀速运动时受到四个力的作用：重力mg、推力F、支持力FN、摩擦力Fµ．沿水平方向建立x轴，将F进行正交分解如图(这样建立坐标系只需分解F)，由于木块做匀速直线运动，所以，在x轴上，向左的力等于向右的力（水平方向二力平衡）；在y轴上向上的力等于向下的力（竖直方向二力平衡）．即 Fcosθ＝Fµ ①‎ FN＝mg+Fsinθ ②‎ 又由于Fµ＝µFN ③‎ ‎∴Fµ＝µ（mg+Fsinθ） 故Ｂ、Ｄ答案是正确的．‎ 小结：（1）在分析同一个问题时，合矢量和分矢量不能同时使用。也就是说，在分析问题时，考虑了合矢量就不能再考虑分矢量；考虑了分矢量就不能再考虑合矢量。‎ ‎（2）矢量的合成分解，一定要认真作图。在用平行四边形定则时，分矢量和合矢量要画成带箭头的实线，平行四边形的另外两个边必须画成虚线。‎ ‎（3）各个矢量的大小和方向一定要画得合理。‎ ‎（4）在应用正交分解时，两个分矢量和合矢量的夹角一定要分清哪个是大锐角，哪个是小锐角，不可随意画成45°。（当题目规定为45°时除外）‎ 三、综合应用举例 ‎【例6】水平横粱的一端A插在墙壁内，另一端装有一小滑轮B，一轻绳的一端C固定于墙上，另一端跨过滑轮后悬挂一质量m=‎10 kg的重物，∠CBA＝30°，如图甲所示，则滑轮受到绳子的作用力为（g=‎10m/s2）‎ A．50N B．50N C．100N D．100N 解析：取小滑轮作为研究对象，悬挂重物的绳中的弹力是T＝mg=10×10N=100 N，故小滑轮受绳的作用力沿BC、BD方向的大小都是100N，分析受力如图（乙）所示． ∠CBD＝120°，∠CBF＝∠DBF，∴∠CBF=60°，⊿CBF是等边三角形．故F＝100 N。故选C。‎ θ O P mg Eq ‎【例7】已知质量为m、电荷为q的小球，在匀强电场中由静止释放后沿直线OP向斜下方运动（OP和竖直方向成θ角），那么所加匀强电场的场强E的最小值是多少？‎ 解析：根据题意，释放后小球所受合力的方向必为OP方向。用三角形定则从右图中不难看出：重力矢量OG的大小方向确定后，合力F的方向确定（为OP方向），而电场力Eq的矢量起点必须在G点，终点必须在OP射线上。在图中画出一组可能的电场力，不难看出，只有当电场力方向与OP方向垂直时Eq才会最小，所以E也最小，有E =‎ ‎【例8】轻绳AB总长l，用轻滑轮悬挂重G的物体。绳能承受的最大拉力是2G，将A端固定，将B端缓慢向右移动d而使绳不断，求d的最大可能值。‎ 解：以与滑轮接触的那一小段绳子为研究对象，在任何一个平衡位置都在滑轮对它的压力（大小为G）和绳的拉力F1、F2共同作用下静止。而同一根绳子上的拉力大小F1、F2总是相等的，它们的合力N是压力G的平衡力，方向竖直向上。因此以F1、F2为分力做力的合成的平行四边形一定是菱形。利用菱形对角线互相垂直平分的性质，结合相似形知识可得 d∶l =∶4，所以d最大为 FB G F α A B v a ‎【例9】 A的质量是m，A、B始终相对静止，共同沿水平面向右运动。当a1=0时和a2=‎0.75g时，‎ B对A的作用力FB各多大？ ‎ 解析：一定要审清题：B对A的作用力FB是B对A的支持力和摩擦力的合力。而A所受重力G=mg和FB的合力是F=ma。‎ 当a1=0时，G与 FB二力平衡，所以FB大小为mg，方向竖直向上。‎ 当a2=‎0.75g时，用平行四边形定则作图：先画出重力（包括大小和方向），再画出A所受合力F的大小和方向，再根据平行四边形定则画出FB。由已知可得FB的大小FB=1.25mg，方向与竖直方向成37o角斜向右上方。‎ ‎【例10】一根长‎2m，重为G的不均匀直棒AB，用两根细绳水平悬挂在天花板上，如图所示，求直棒重心C的位置。‎ 解析：当一个物体受三个力作用而处于平衡状态，如果其中两个力的作用线相交于一点．则第三个力的作用线必通过前两个力作用线的相交点，把O‎1A和O2B延长相交于O点，则重心C一定在过O点的竖直线上，如图所示由几何知识可知：‎ BO=AB/2=‎1m BC=BO/2=‎‎0.5m 故重心应在距B端 ‎0.5m处。‎ ‎【例11】如图（甲）所示．质量为m的球放在倾角为α的光滑斜面上，试分析挡板AO与斜面间的倾角β为多大时，AO所受压力最小？‎ 解析：虽然题目问的是挡板AO的受力情况，但若直接以挡板为研究对象，因挡板所受力均为未知力，将无法得出结论．以球为研究对象，球所受重力产生的效果有两个：对斜面产生的压力N1、对挡板产生的压力 N2，根据重力产生的效果将重力分解，如图（乙）所示，‎ 当挡板与斜面的夹角β由图示位置变化时，N1大小改变但方向不变，始终与斜面垂直，N2的大小和方向均改变，如图（乙）中虚线由图可看出挡板AO与斜面垂直时β=90°时，挡板AO所受压力最小，最小压力N2min =mgsinα。‎ 针对训练 ‎1如图所示．有五个力作用于一点P，构成一个正六边形的两个所示，‎ 邻边和三条对角线，设F3=10N，则这五个力的合力大小为（ ）‎ A．10（2＋）N B．20N ‎ C．30N D．0‎ ‎2．关于二个共点力的合成．下列说法正确的是 （ ）‎ A．合力必大于每一个力 B．合力必大于两个力的大小之和 C．合力的大小随两个力的夹角的增大而减小 D．合力可以和其中一个力相等，但小于另一个力 ‎3．如图所示 质量为m的小球被三根相同的轻质弹簧a、b、c拉住，c竖直向下a、b、c三者夹角都是120°，小球平衡时，a、b、c伸长的长度之比是3∶3∶1，则小球受c的拉力大小为 （ ）‎ A．mg B．0.5mg ‎ C．1.5mg D．3mg ‎4．如图所示．物体处于平衡状态，若保持a不变，当力F与水平方向夹角β多大时F有最小值 （ ）‎ A．β＝0 B．β＝‎ C．β＝α D．β＝2α ‎5．如图所示一条易断的均匀细绳两端固定在天花板的A、B两点，今在细绳O处吊一砝码，如果OA＝2BO，则 （ ）‎ A．增加硅码时，AO绳先断 B．增加硅码时，BO绳先断 C．B端向左移，绳子易断 D．B端向右移，绳子易断 ‎6．图所示，A、A′两点很接近圆环的最高点．BOB′为橡皮绳，∠BOB′＝120°，且B、B′与OA对称．在点O挂重为G的物体，点O在圆心，现将B、B′两端分别移到同一圆周上的点A、A′，若要使结点O的位置不变，则物体的重量应改为 A．G B．‎ C． D．‎‎2G ‎7．长为L的轻绳，将其两端分别固定在相距为d的两坚直墙面上的A、B两点。一小滑轮O跨过绳子下端悬挂一重力为G的重物C，平衡时如图所示，求AB绳中的张力。‎ ‎ ‎ ‎8如图所示，质量为m，横截面为直角形的物快ABC，∠ABC＝α，AB边靠在竖直墙上，F是垂直于斜面BC的推力，现物块静止不动，求摩擦力的大小。‎ 参考答案 ‎1．C 2．C 3．B 4．C 5．BD 6．D ‎7．FT＝ 8．f=mg+Fsinα