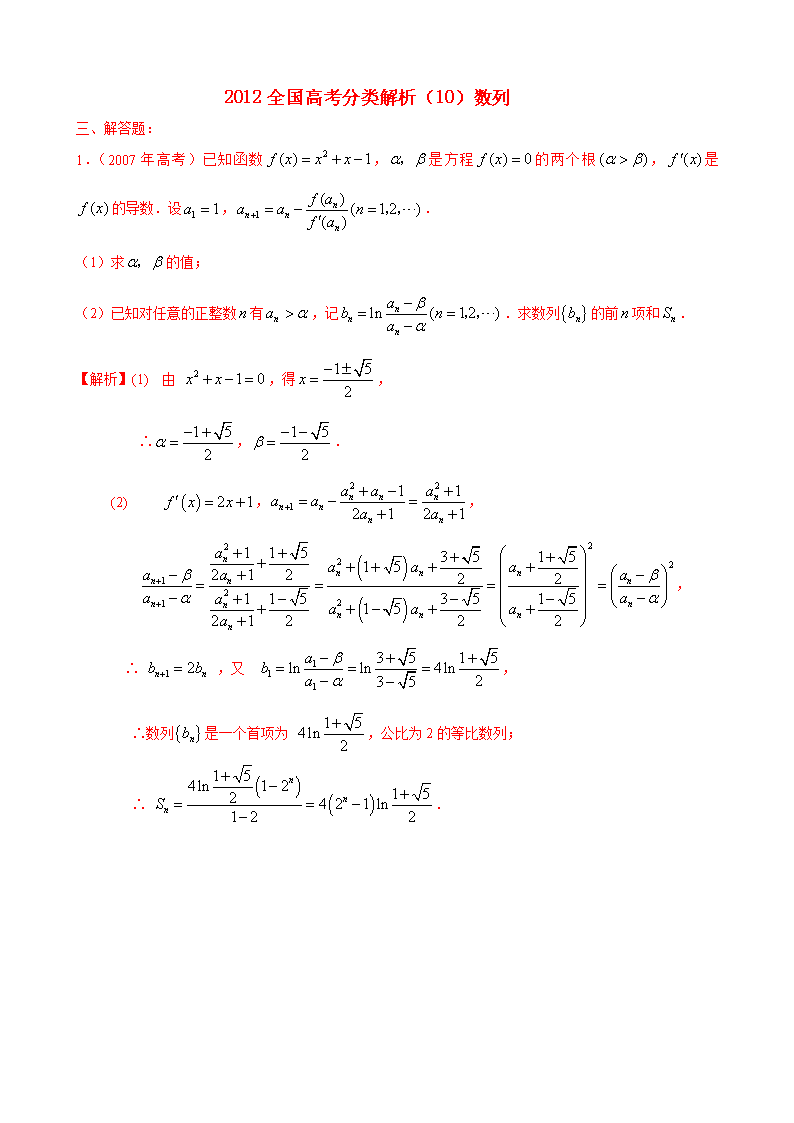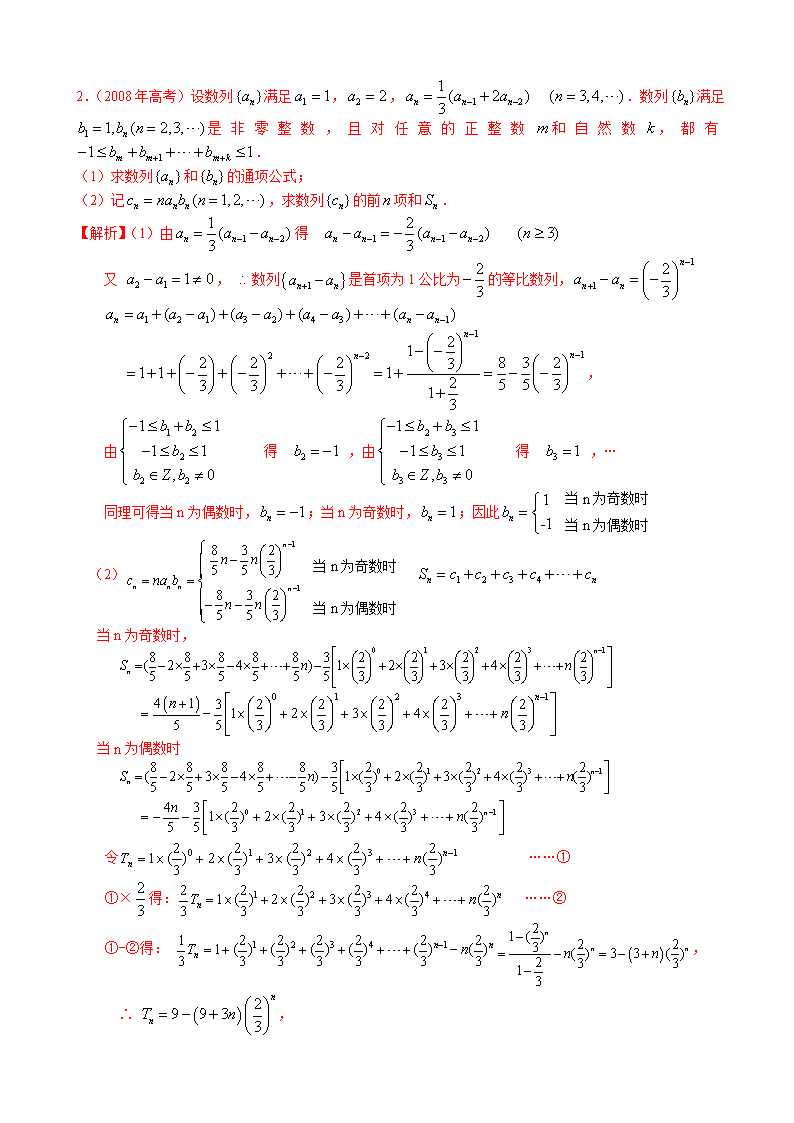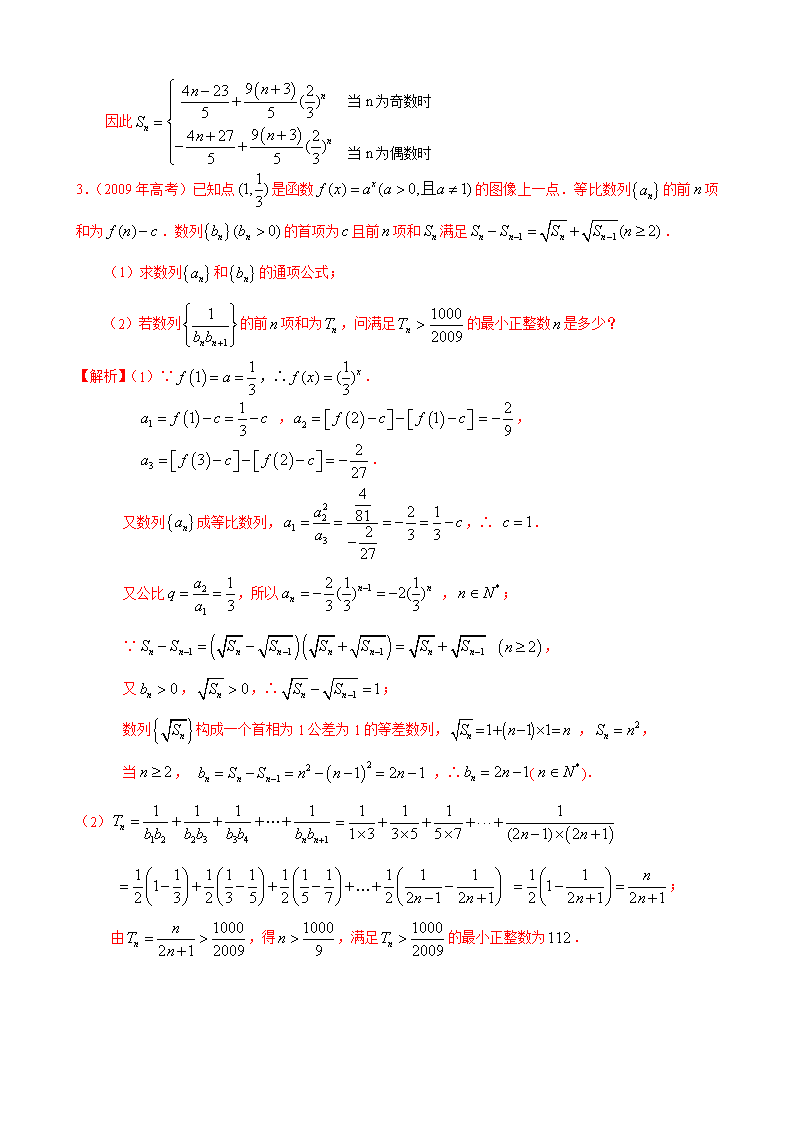广东高考试题分类汇编10数列解答题 7页

‎2012全国高考分类解析（10）数列 三、解答题：‎ ‎1．（2007年高考）已知函数，是方程的两个根，是的导数．设，．‎ ‎（1）求的值；‎ ‎（2）已知对任意的正整数有，记．求数列的前项和．‎ ‎【解析】(1) 由 ，得，‎ ‎ ∴，．‎ ‎ (2) ，，‎ ‎ ，‎ ‎ ∴ ，又 ，‎ ‎∴数列是一个首项为 ，公比为2的等比数列；‎ ‎∴ ．‎ ‎2．（2008年高考）设数列满足，， ．数列满足是非零整数，且对任意的正整数和自然数，都有．‎ ‎（1）求数列和的通项公式；‎ ‎（2）记，求数列的前项和．‎ ‎【解析】（1）由得 ‎ 又 ， 数列是首项为1公比为的等比数列， ‎ ‎ ，‎ 当n为奇数时 当n为偶数时 ‎ 由 得 ，由 得 ，…‎ ‎ 同理可得当n为偶数时，；当n为奇数时，；因此 当n为奇数时 当n为偶数时 ‎ （2） ‎ 当n为奇数时，‎ ‎ ‎ 当n为偶数时 令 ……①‎ ‎①×得： ……②‎ ‎①-②得： ， ‎ ‎ ∴ ，‎ 当n为奇数时 当n为偶数时 因此 ‎ ‎3．（2009年高考）已知点是函数的图像上一点．等比数列的前项和为．数列的首项为且前项和满足．‎ ‎（1）求数列和的通项公式； ‎ ‎ （2）若数列的前项和为，问满足的最小正整数是多少？‎ ‎【解析】（1）∵，∴．‎ ‎ ，，‎ ‎ ．‎ 又数列成等比数列，，∴ ．‎ 又公比，所以 ，；‎ ‎∵ ，‎ 又，，∴；‎ 数列构成一个首相为1公差为1的等差数列， ，，‎ 当， ，∴()．‎ ‎（2） ‎ ； ‎ ‎ 由，得，满足的最小正整数为．‎ ‎4．（2011年高考） 设b>0，数列满足，．‎ ‎（1）求数列的通项公式；‎ ‎（2）证明：对于一切正整数，．‎ ‎ 【解析】∵，∴，∴，‎ ‎ 当时， ∴， ‎ ‎ ∴当时，是以为首项，公差为1的等差数列，‎ ‎ ∴， ∴． ∵也符合， ∴，．‎ ‎ 当时， 令， ∴， ∴， ‎ ‎ ∴ ∴，‎ ‎ ∴当时，是以为首项，公比为的等比数列，‎ ‎∴， ∴ ．‎ ‎ ∵也符合， ∴，．‎ ‎ 综上：当时，，． 当时，，．‎ （2） 证明：当时，，．‎ ‎ ∴对于一切正整数，．‎ ‎ 当时， ∴， ∴要证．‎ ‎ 即证． 即证．‎ ‎ 即证．‎ ‎ 即证．‎ ‎ 设， ‎ ‎ ∴ ‎ ‎ ‎ ∴根据均值不等式得：‎ ‎ ‎ ．‎ ‎ ∴当时，对于一切正整数，．‎ ‎ 综上：对于一切正整数，．‎ ‎5．（2012年高考）设数列的前项和为，数列的前项和为，满足．‎ ‎（1）求的值；‎ ‎（2）求数列的通项公式．‎ ‎【解析】（1）当时，，‎ ‎∵，∴，∴，‎ ‎(2)当时，‎ ，‎ ‎∵当时，‎ ‎∴，‎ ‎∴，‎ ‎ ∴数列是以为首项，为公比的等比数列，‎ ‎ ∴，∴，‎ ‎ ∵，‎ ‎∴，． ‎ ‎6．（2013）‎ 设各项均为正数的数列的前项和为，满足且构成等比数列．‎ ‎(1) 证明：；‎ ‎(2) 求数列的通项公式；‎ ‎(3) 证明：对一切正整数，有 ‎6、（1）当时，， ‎ ‎（2）当时，， , 当时，是公差的等差数列.‎ 构成等比数列，，，解得,‎ 由（1）可知， 是首项,公差的等差数列.‎ ‎ 数列的通项公式为.‎ ‎（3）