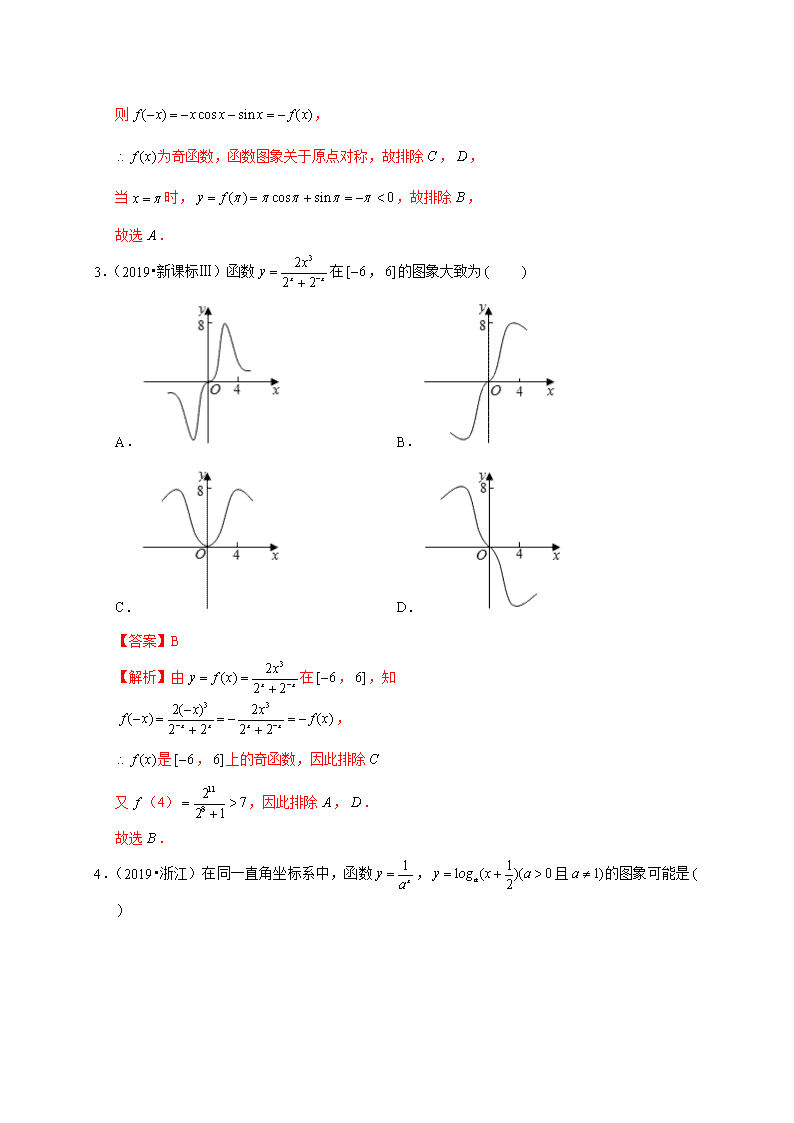2020-2021学年高考数学（理）考点：函数的图象 26页

‎2020-2021学年高考数学（理）考点：函数的图象 ‎1．描点法作图 方法步骤：(1)确定函数的定义域．(2)化简函数的解析式．(3)讨论函数的性质即奇偶性、周期性、单调性、最值(甚至变化趋势)．(4)描点连线，画出函数的图象．‎ ‎2．图象变换 ‎(1)平移变换 ‎(2)对称变换 ‎①y＝f (x)y＝－f (x)．‎ ‎②y＝f (x)y＝f (－x)．‎ ‎③y＝f (x)y＝－f (－x)．‎ ‎④y＝ax (a>0且a≠1)y＝logax(a>0且a≠1)．‎ ‎(3)伸缩变换 ‎①y＝f (x) y＝f (x)．‎ ‎②y＝f (x) y＝af (x)．‎ ‎(4)翻折变换 ‎①y＝f (x)y＝|f (x)|.‎ ‎②y＝f (x)y＝f (|x|)．‎ 概念方法微思考 ‎1．函数f (x)的图象关于直线x＝a对称，你能得到f (x)解析式满足什么条件？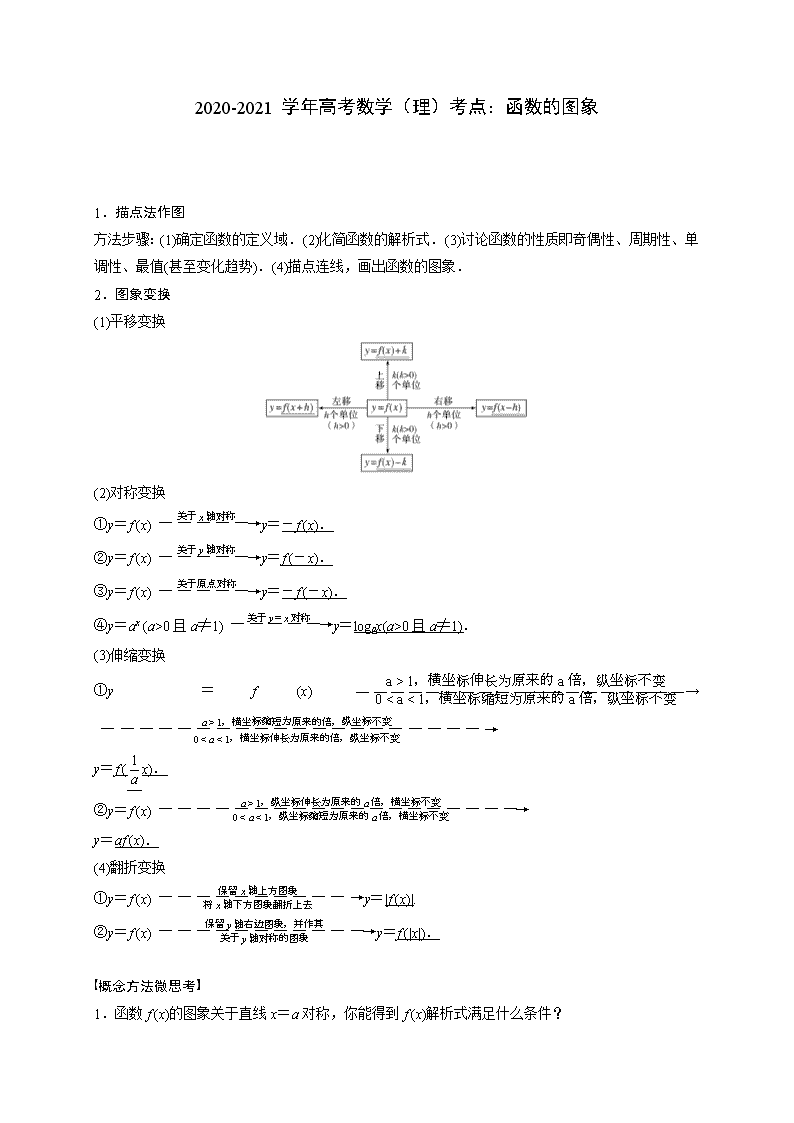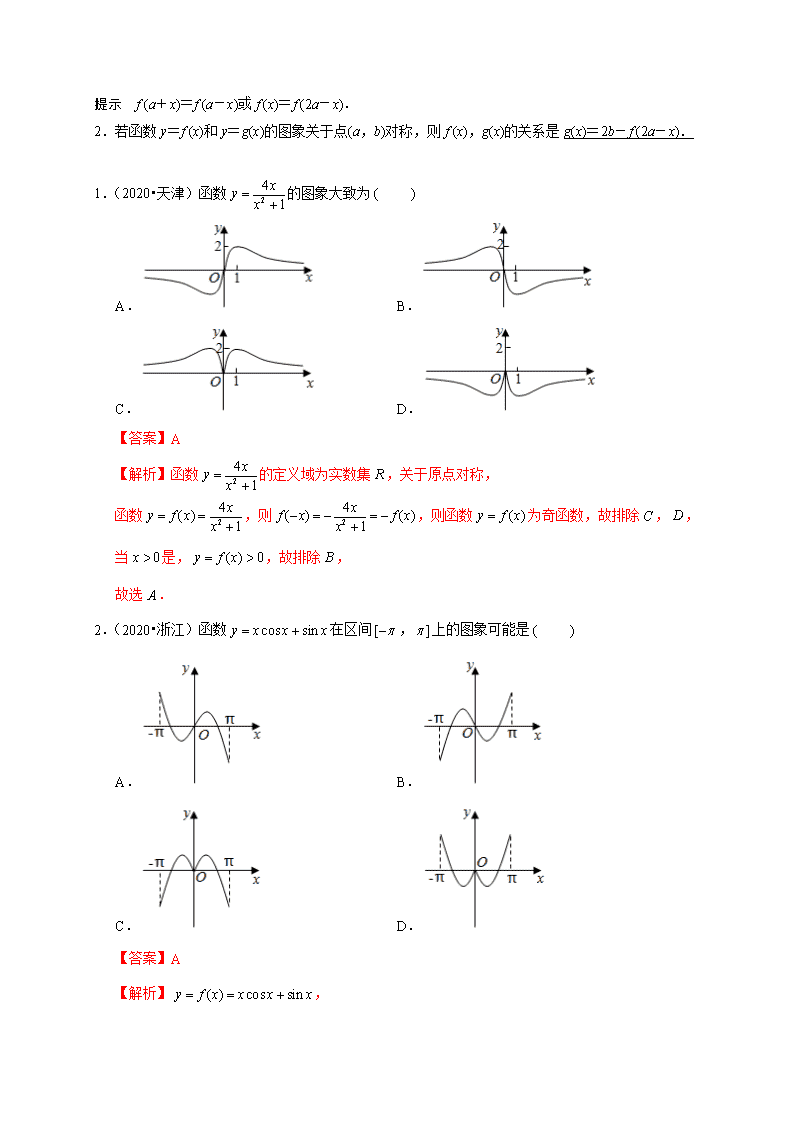‎ 提示　f (a＋x)＝f (a－x)或f (x)＝f (2a－x)．‎ ‎2．若函数y＝f (x)和y＝g(x)的图象关于点(a，b)对称，则f (x)，g(x)的关系是g(x)＝2b－f (2a－x)．‎ ‎1．（2020•天津）函数的图象大致为　　‎ A． B． ‎ C． D．‎ ‎【答案】A ‎【解析】函数的定义域为实数集，关于原点对称，‎ 函数，则，则函数为奇函数，故排除，，‎ 当是，，故排除，‎ 故选．‎ ‎2．（2020•浙江）函数在区间，上的图象可能是　　‎ A． B． ‎ C． D．‎ ‎【答案】A ‎【解析】，‎ 则，‎ 为奇函数，函数图象关于原点对称，故排除，，‎ 当时，，故排除，‎ 故选．‎ ‎3．（2019•新课标Ⅲ）函数在，的图象大致为　　‎ A． B． ‎ C． D．‎ ‎【答案】B ‎【解析】由在，，知 ‎，‎ 是，上的奇函数，因此排除 又（4），因此排除，．‎ 故选．‎ ‎4．（2019•浙江）在同一直角坐标系中，函数，且的图象可能是　　‎ A． B． ‎ C． D．‎ ‎【答案】D ‎【解析】由函数，，‎ 当时，可得是递减函数，图象恒过点，‎ 函数，是递增函数，图象恒过，；‎ 当时，可得是递增函数，图象恒过点，‎ 函数，是递减函数，图象恒过，；‎ 满足要求的图象为：‎ 故选．‎ ‎5．（2019•新课标Ⅰ）函数在，的图象大致为　　‎ A． B． ‎ C． D．‎ ‎【答案】D ‎【解析】，，，‎ ‎，‎ 为，上的奇函数，因此排除；‎ 又，因此排除，；‎ 故选．‎ ‎6．（2018•新课标Ⅱ）函数的图象大致为　　‎ A． B． ‎ C． D．‎ ‎【答案】B ‎【解析】函数，‎ 则函数为奇函数，图象关于原点对称，排除，‎ 当时，（1），排除．‎ 当时，，排除，‎ 故选．‎ ‎7．（2018•新课标Ⅲ）下列函数中，其图象与函数的图象关于直线对称的是　　‎ A． B． C． D．‎ ‎【答案】B ‎【解析】首先根据函数的图象，‎ 则：函数的图象与的图象关于轴对称．‎ 由于函数的图象关于直线对称．‎ 则：把函数的图象向右平移2个单位即可得到：．‎ 即所求得解析式为：．‎ 故选．‎ ‎8．（2018•浙江）函数的图象可能是　　‎ A． B． ‎ C． D．‎ ‎【答案】D ‎【解析】根据函数的解析式，得到：函数的图象为奇函数，‎ 故排除和．‎ 当时，函数的值也为0，‎ 故排除．‎ 故选．‎ ‎9．（2018•上海）设是含数1的有限实数集，是定义在上的函数，若 的图象绕原点逆时针旋转后与原图象重合，则在以下各项中，（1）的可能取值只能是　　‎ A． B． C． D．0‎ ‎【答案】B ‎【解析】由题意得到：问题相当于圆上由12个点为一组，每次绕原点逆时针旋转个单位后与下一个点会重合．‎ 我们可以通过代入和赋值的方法当（1），，0时，‎ 此时得到的圆心角为，，0，‎ 然而此时或者时，‎ 都有2个与之对应，‎ 而我们知道函数的定义就是要求一个只能对应一个，‎ 因此只有当，‎ 此时旋转，‎ 此时满足一个只会对应一个，‎ 因此答案就选：．‎ 故选．‎ ‎10．（2018•新课标Ⅲ）函数的图象大致为　　‎ A． B． ‎ C． D．‎ ‎【答案】D ‎【解析】函数过定点，排除，．‎ 函数的导数，‎ 由得，‎ 得或，此时函数单调递增，‎ 由得，‎ 得或，此时函数单调递减，排除，‎ 也可以利用（1），排除，，‎ 故选．‎ ‎11．（2017•山东）已知当，时，函数 的图象与的图象有且只有一个交点，则正实数的取值范围是　　‎ A．，， B．，， ‎ C．， D．，，‎ ‎【答案】B ‎【解析】根据题意，由于为正数， 为二次函数，在区间为减函数，，为增函数，‎ 函数为增函数，‎ 分2种情况讨论：‎ ‎①、当时，有，‎ 在区间，上， 为减函数，且其值域为，，‎ 函数为增函数，其值域为，，‎ 此时两个函数的图象有1个交点，符合题意；‎ ‎②、当时，有，‎ ‎ 在区间为减函数，，为增函数，‎ 函数为增函数，其值域为，，‎ 若两个函数的图象有1个交点，则有，‎ 解可得或，‎ 又由为正数，则；‎ 综合可得：的取值范围是，，；‎ 故选．‎ ‎12．（2017•新课标Ⅲ）函数的部分图象大致为　　‎ A． B． ‎ C． D．‎ ‎【答案】D ‎【解析】函数，可知：是奇函数，所以函数的图象关于原点对称，‎ 则函数的图象关于对称，‎ 当，，排除、，当时，，排除．‎ 故选．‎ ‎13．（2017•浙江）函数的导函数的图象如图所示，则函数的图象可能是　　‎ A． B． C． D．‎ ‎【答案】D ‎【解析】由当时，函数单调递减，当时，函数单调递增，‎ 则由导函数的图象可知：先单调递减，再单调递增，然后单调递减，最后单调递增，排除，，‎ 且第二个拐点（即函数的极大值点）在轴上的右侧，排除，‎ 故选．‎ ‎14．（2017•新课标Ⅰ）函数的部分图象大致为　　‎ A． B． ‎ C． D．‎ ‎【答案】C ‎【解析】函数，‎ 可知函数是奇函数，排除选项，‎ 当时，，排除，‎ 时，，排除．‎ 故选．‎ ‎15．（2017•新课标Ⅰ）已知函数，则　　‎ A．在单调递增 B．在单调递减 ‎ C．的图象关于直线对称 D．的图象关于点对称 ‎【答案】C ‎【解析】函数，‎ ‎，‎ 即，‎ 即的图象关于直线对称，‎ 故选．‎ ‎16．（2020•北京）为满足人民对美好生活的向往，环保部门要求相关企业加强污水治理，排放未达标的企业要限期整改．设企业的污水排放量与时间的关系为，用的大小评价在，‎ 这段时间内企业污水治理能力的强弱．已知整改期内，甲、乙两企业的污水排放量与时间的关系如图所示．‎ 给出下列四个结论：‎ ‎①在，这段时间内，甲企业的污水治理能力比乙企业强；‎ ‎②在时刻，甲企业的污水治理能力比乙企业强；‎ ‎③在时刻，甲，乙两企业的污水排放都已达标；‎ ‎④甲企业在，，，，，这三段时间中，在，的污水治理能力最强．‎ 其中所有正确结论的序号是__________．‎ ‎【答案】①②③‎ ‎【解析】设甲企业的污水排放量与时间的关系为，乙企业的污水排放量与时间的关系为．‎ 对于①，在，这段时间内，甲企业的污水治理能力为，‎ 乙企业的污水治理能力为．‎ 由图可知，，，‎ 即甲企业的污水治理能力比乙企业强，故①正确；‎ 对于②，由图可知，在时刻的切线的斜率小于在时刻的切线的斜率，但两切线斜率均为负值，‎ 在时刻，甲企业的污水治理能力比乙企业强，故②正确；‎ 对于③，在时刻，甲，乙两企业的污水排放都小于污水达标排放量，‎ 在时刻，甲，乙两企业的污水排放都已达标，故③正确；‎ 对于④，由图可知，甲企业在，，，，，这三段时间中，在，‎ 的污水治理能力最强，‎ 故④错误．‎ 正确结论的序号是①②③．‎ 故答案为：①②③．‎ ‎17．（2018•上海）已知常数，函数的图象经过点，．若，则__________．‎ ‎【答案】6‎ ‎【解析】函数的图象经过点，．‎ 则：，‎ 整理得：，‎ 解得：，‎ 由于：，‎ 所以：，‎ 由于，‎ 故：．‎ 故答案为：6．‎ ‎18．（2017•北京）三名工人加工同一种零件，他们在一天中的工作情况如图所示，其中的横、纵坐标分别为第名工人上午的工作时间和加工的零件数，点的横、纵坐标分别为第名工人下午的工作时间和加工的零件数，，2，3．‎ ‎（1）记为第名工人在这一天中加工的零件总数，则，，中最大的是__________．‎ ‎（2）记为第名工人在这一天中平均每小时加工的零件数，则，，中最大的是__________．‎ ‎【答案】，‎ ‎【解析】（1）若为第名工人在这一天中加工的零件总数，‎ 的纵坐标的纵坐标；‎ 的纵坐标的纵坐标，‎ 的纵坐标的纵坐标，‎ 由已知中图象可得：，，中最大的是，‎ ‎（2）若为第名工人在这一天中平均每小时加工的零件数，‎ 则为中点与原点连线的斜率，‎ 故，，中最大的是 故答案为：，．‎ ‎1．（2020•江西模拟）函数的图象不可能是　　‎ A． B． ‎ C． D．‎ ‎【答案】C ‎【解析】，选项中，图象关于原点对称，‎ 为奇函数，即，即，‎ ‎，‎ 当时，的图象为选项；当时，的图象为选项；‎ 而，选项中，图象关于轴对称，所以为偶函数，即，即，‎ ‎，‎ 当时，，故的图象为选项，不可能为选项．‎ 故选．‎ ‎2．（2020•镜湖区校级模拟）函数的大致图象为　　‎ A． B． C． D．‎ ‎【答案】B ‎【解析】，则是奇函数，则图象关于原点对称，排除，‎ ‎（1），排除，‎ 当，，，由指数爆炸的性质可知，‎ 则，排除，‎ 故选．‎ ‎3．（2020•武昌区校级模拟）函数在，的图象大致为　　‎ A． B． ‎ C． D．‎ ‎【答案】D ‎【解析】函数，‎ 当时，，故排除，‎ 当时，，故排除，‎ 当时，，故排除，‎ 故选．‎ ‎4．（2020•梅河口市校级模拟）函数的部分图象大致是　　‎ A． B． ‎ C． D．‎ ‎【答案】A ‎【解析】 的定义域为，‎ 因为，‎ 所以 为偶函数，故排除．‎ 当 时，有，故，‎ 而，故，从而排除，．‎ 故选．‎ ‎5．（2020•道里区校级四模）函数的图象大致为　　‎ A． B． ‎ C． D．‎ ‎【答案】A ‎【解析】函数的定义域为，当时，，排除，，‎ 当时，，排除，‎ 故选．‎ ‎6．（2020•运城模拟）函数的部分图象大致是　　‎ A． B． ‎ C． D．‎ ‎【答案】B ‎【解析】根据题意，函数，其定义域为，因为，所以是偶函数，排除选项；‎ 当时，，当时，，故排除选项，．‎ 故选．‎ ‎7．（2020•龙凤区校级模拟）函数的图象大致是　　‎ A． B． ‎ C． D．‎ ‎【答案】C ‎【解析】根据题意，对于函数，有，解可得或，即函数的定义域为或，排除，‎ 又由（2），排除；‎ 故选．‎ ‎8．（2020•杜集区校级模拟）函数的部分图象大致为　　‎ A． B． ‎ C． D．‎ ‎【答案】A ‎【解析】根据题意，函数，其定义域为，，则是偶函数，排除、，‎ ‎，其导数，有，排除；排除，‎ 故选．‎ ‎9．（2020•雨花区校级模拟）函数的图象大致是　　‎ A． B． ‎ C． D．‎ ‎【答案】D ‎【解析】，‎ ‎，‎ 令得到．‎ 故函数在上，，函数单调递减，‎ 在上，，函数单调递减，‎ 在上，，函数单调递增．‎ 令，．对比图象知：满足条件，‎ 故选．‎ ‎10．（2020•河南模拟）函数的图象大致为　　‎ A． B． ‎ C． D．‎ ‎【答案】D ‎【解析】根据题意，函数，则（1），排除，‎ ‎，排除，‎ 故选．‎ ‎11．（2020•河南模拟）函数的图象大致为　　‎ A． B． ‎ C． D．‎ ‎【答案】D ‎【解析】根据题意，函数，‎ 则（1），排除，‎ ‎，排除，‎ 故选．‎ ‎12．（2020•庐阳区校级模拟）已知函数的图象如图所示，则该函数的解析式可能是　　‎ A． B． ‎ C． D．‎ ‎【答案】D ‎【解析】由图象可知，是非奇非偶函数，排除；‎ 当时，图象在轴的上方，，，排除，；‎ 故选．‎ ‎13．（2020•浙江模拟）在直角坐标系中，函数的图象如图所示，则可能取值是　　‎ A． B． C．1 D．0‎ ‎【答案】C ‎【解析】若，则恒成立，与存在负值矛盾，排除，‎ 若，则当时，恒成立，与存在负值矛盾，排除、，‎ 故选．‎ ‎14．（2020•聊城三模）函数的图象大致是　　‎ A． B． ‎ C． D．‎ ‎【答案】C ‎【解析】，‎ 函数的定义域为，‎ ‎，‎ 则是偶函数，图象关于轴对称，排除，，‎ 当且，，排除，‎ 故选．‎ ‎15．（2020•沙坪坝区校级模拟）函数的图象大致为　　‎ A． B． C． D．‎ ‎【答案】A ‎【解析】函数的定义域为，‎ ‎，则是奇函数，图象关于圆的对称，排除，，‎ 当时，恒成立，排除，‎ 故选．‎ ‎16．（2020•绥化模拟）函数在内的图象大致为　　‎ A． B． ‎ C． D．‎ ‎【答案】A ‎【解析】，则是偶函数，图象关于轴对称，排除，‎ 当时，，排除，‎ 故选．‎ ‎17．（2020•平阳县模拟）函数的导函数的图象大致如图，则可能是　　‎ A． B． ‎ C． D．‎ ‎【答案】A ‎【解析】根据题意，依次分析4个选项：‎ 对于，对于，其导数，‎ 有，‎ 即为奇函数，‎ 又由，‎ 在区间上，，为减函数，在区间，上，，为增函数，‎ 故符合；‎ 对于，对于，‎ 则，则为奇函数，‎ 又由，‎ 在区间上，，为增函数，‎ 故不符合；‎ 对于，对于，则，‎ 有且，则为非奇非偶函数，‎ 故不符合，‎ 对于，对于，则，‎ 有且，则为非奇非偶函数，‎ 故不符合 故选．‎ ‎18．（2020•四川模拟）函数的大致图象是　　‎ A． B． ‎ C． D．‎ ‎【答案】D ‎【解析】因为，所以为奇函数，排除选项和；‎ 当时，，排除选项．‎ 故选．‎ ‎19．（2020•浙江模拟）已知函数的部分图象如图所示，则　　‎ A． B． C． D．‎ ‎【答案】B ‎【解析】由，得，‎ 令，由图可知该方程一个根在之间，一个根大于1．‎ 且二次函数的图象开口向下，则，故错误；‎ ‎，故错误；‎ ‎（1），故正确；‎ ‎，则，故错误．‎ 故选．‎ ‎20．（2020•厦门模拟）已知函数的图象如图，则　　‎ A．， B．， C．， D．，‎ ‎【答案】D ‎【解析】由图可知，，即，；‎ 且函数有2个极值点，有2个变号零点，‎ 当时，，则的零点问题可转化为函数和有两个交点，‎ 令，则，‎ 当或时，，函数单调递减，‎ 当时，，函数单调递增，‎ ‎（1），‎ 若与有两个交点，则前提条件为，和异号，‎ ‎，，‎ 故选．‎