高考数学理科一轮复习经典例题——直线与平面的平行判定和性质 18页

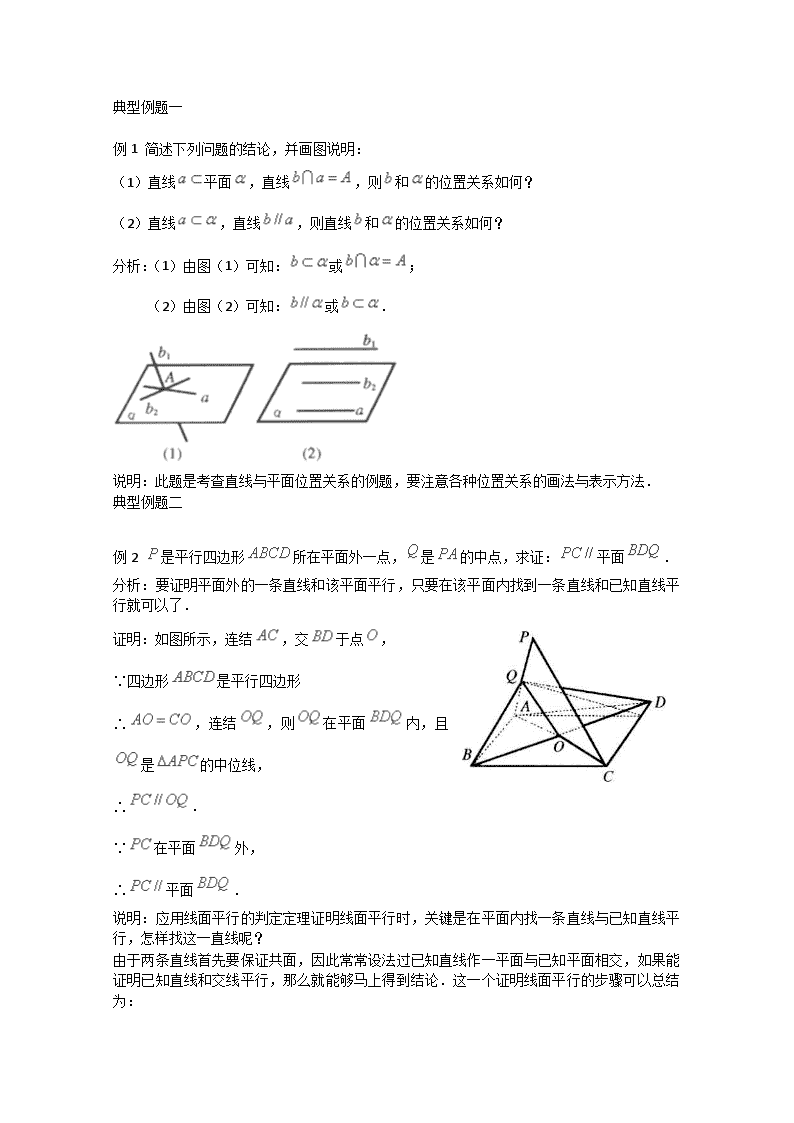
典型例题一 例1 简述下列问题的结论，并画图说明：‎ ‎（1）直线平面，直线，则和的位置关系如何？‎ ‎（2）直线，直线，则直线和的位置关系如何？‎ 分析：（1）由图（1）可知：或；‎ ‎ （2）由图（2）可知：或．‎ 说明：此题是考查直线与平面位置关系的例题，要注意各种位置关系的画法与表示方法．‎ 典型例题二 例2 是平行四边形所在平面外一点，是的中点，求证：平面．‎ 分析：要证明平面外的一条直线和该平面平行，只要在该平面内找到一条直线和已知直线平行就可以了．‎ 证明：如图所示，连结，交于点，‎ ‎∵四边形是平行四边形 ‎∴，连结，则在平面内，且是的中位线，‎ ‎∴． ‎ ‎∵在平面外，‎ ‎∴平面．‎ 说明：应用线面平行的判定定理证明线面平行时，关键是在平面内找一条直线与已知直线平行，怎样找这一直线呢？‎ 由于两条直线首先要保证共面，因此常常设法过已知直线作一平面与已知平面相交，如果能证明已知直线和交线平行，那么就能够马上得到结论．这一个证明线面平行的步骤可以总结为：‎ 过直线作平面，得交线，若线线平行，则线面平行．‎ 典型例题三 例3 经过两条异面直线，之外的一点，可以作几个平面都与，平行？并证明你的结论．‎ 分析：可考虑点的不同位置分两种情况讨论．‎ 解：（1）当点所在位置使得，（或，）本身确定的平面平行于（或）时，过点再作不出与，都平行的平面；‎ ‎（2）当点所在位置，（或，）本身确定的平面与（或）不平行时，可过点作，．由于，异面，则，不重合且相交于．由于，，确定的平面，则由线面平行判定定理知：，．可作一个平面都与，平行．‎ 故应作“0个或1个”平面．‎ 说明：本题解答容易忽视对点的不同位置的讨论，漏掉第（1）种情况而得出可作一个平面的错误结论．可见，考虑问题必须全面，应区别不同情形分别进行分类讨论．‎ 典型例题四 例4 平面外的两条平行直线中的一条平行于这个平面，那么另一条直线也平行于这个平面．‎ 已知：直线，平面，．‎ 求证：．‎ 证明：如图所示，过及平面内一点作平面．‎ 设，‎ ‎∵，‎ ‎∴．‎ 又∵，‎ ‎∴．‎ ‎∵，，‎ ‎∴．‎ 说明：根据判定定理，只要在内找一条直线，根据条件，为了利用直线和平面平行的性质定理，可以过作平面与相交，我们常把平面称为辅助平面，它可以起到桥梁作用，把空间问题向平面问题转化．‎ 和平面几何中添置辅助线一样，在构造辅助平面时，首先要确认这个平面是存在的，例如，本例中就是以“直线及直线外一点确定一个平面”为依据来做出辅助平面的．‎ 典型例题五 例5 已知四面体的所有棱长均为．求：‎ ‎（1）异面直线的公垂线段及的长；‎ ‎（2）异面直线和所成的角．‎ 分析：依异面直线的公垂线的概念求作异面直线的公垂线段，进而求出其距离；对于异面直线所成的角可采取平移构造法求解．‎ 解：（1）如图，分别取的中点，连结．‎ 由已知，得≌．‎ ‎∴，是的中点，‎ ‎∴．‎ 同理可证 ‎∴是的公垂线段．‎ 在中，，． ‎ ‎∴‎ ‎ ．‎ ‎（2）取的中点，连结，则．‎ ‎∴和所成的锐角或直角就是异面直线和所成的角．‎ 连结，在中，，，．‎ 由余弦定理，得 ‎．‎ ‎∴．‎ 故异面直线和所成的角为．‎ 说明：对于立体几何问题要注意转化为平面问题来解决，同时要将转化过程简要地写出来，然后再求值．‎ 典型例题六 例6　如果一条直线与一个平面平行，那么过这个平面内的一点且与这条直线平行的直线必在这个平面内．‎ 已知：直线，，，．‎ 求证：．‎ 分析：由于过点与平行的直线是惟一存在的，因此，本题就是要证明，在平面外，不存在过与平行的直线，这是否定性命题，所以使用反证法．‎ 证明：如图所示，设，过直线和点作平面，且．‎ ‎∵，∴．‎ 这样过点就有两条直线和同时平行于直线，与平行公理矛盾．‎ ‎∴必在内．‎ 说明：(1)本例的结论可以直接作为证明问题的依据．‎ ‎(2)本例还可以用同一法来证明，只要改变一下叙述方式．‎ 如上图，过直线及点作平面，设．∵，∴．‎ 这样，与都是过点平行于的直线，根据平行公理，这样的直线只有一条，‎ ‎∴与重合．∵，∴．‎ ‎ ‎ 典型例题七 例7 下列命题正确的个数是（　　）．‎ ‎(1)若直线上有无数个点不在平面内，则；‎ ‎(2)若直线平行于平面内的无数条直线，则；‎ ‎(3)若直线与平面平行，则与平面内的任一直线平行；‎ ‎(4)若直线在平面外，则．‎ A．0个　　B．1个　　C．2个　　D．3个 分析：本题考查的是空间直线与平面的位置关系．对三种位置关系定义的准确理解是解本题的关键．要注意直线和平面的位置关系除了按照直线和平面公共点的个数来分类，还可以按照直线是否在平面内来分类．‎ 解：(1)直线上有无数个点不在平面内，并没有说明是所在点都不在平面内，因而直线可能与平面平行亦有可能与直线相交．解题时要注意“无数”并非“所有”．(2)直线虽与内无数条直线平行，但有可能在平面内，所以直线不一定平行．(3)这是初学直线与平面平行的性质时常见错误，借助教具我们很容易看到．当时，若且，则在平面内，除了与平行的直线以外的每一条直线与都是异面直线．(4)直线在平面外，应包括两种情况：和与相交，所以与不一定平行．‎ 故选A．‎ 说明：如果题中判断两条直线与一平面之间的位置关系，解题时更要注意分类要完整，考虑要全面．如直线、都平行于，则与的位置关系可能平行，可能相交也有可能异面；再如直线、，则与的位置关系可能是平行，可能是在内．‎ 典型例题八 例8　如图，求证：两条平行线中的一条和已知平面相交，则另一条也与该平面相交．‎ 已知：直线，．求证：直线与平面相交．‎ 分析：利用转化为平面问题来解决，由可确定一辅助平面，这样可以把题中相关元素集中使用，既创造了新的线面关系，又将三维降至二维，使得平几知识能够运用．‎ 解：∵，‎ ‎∴和可确定平面．‎ ‎∵，‎ ‎∴平面和平面相交于过点的直线．‎ ‎∵在平面内与两条平行直线、中一条直线相交，‎ ‎∴必定与直线也相交，不妨设，又因为不在平面内（若在平面内，则和都过相交直线和，因此与重合，在内，和已知矛盾）．‎ 所以直线和平面相交．‎ 说明：证明直线和平面相交的常用方法有：证明直线和平面只有一个公共点；否定直线在平面内以及直线和平面平行；用此结论：一条直线如果经过平面内一点，又经过平面外一点，则此直线必与平面相交（此结论可用反证法证明）．‎ 典型例题九 例9　如图，求证：经过两条异面直线中的一条，有且仅有一个平面与另一条直线平行．‎ 已知：与是异面直线．求证：过且与平行的平面有且只有一个．‎ 分析：本题考查存在性与唯一性命题的证明方法．解题时要理解“有且只有”的含义．“有”就是要证明过直线存在一个平面，且，“只有”就是要证满足这样条件的平面是唯一的．存在性常用构造法找出（或作出）平面，唯一性常借助于反证法或其它唯一性的结论．‎ 证明：(1)在直线上任取一点，由点和直线可确定平面．‎ 在平面内过点作直线，使，则和为两相交直线，‎ 所以过和可确定一平面．‎ ‎∵，与为异面直线，‎ ‎∴．‎ 又∵，，‎ ‎∴．‎ 故经过存在一个平面与平行．‎ ‎(2)如果平面也是经过且与平行的另一个平面，‎ 由上面的推导过程可知也是经过相交直线和的．‎ 由经过两相交直线有且仅有一个平面的性质可知，平面与重合，‎ 即满足条件的平面是唯一的．‎ 说明：对于两异面直线和，过存在一平面且与平行，同样过也存在一平面且与平行．而且这两个平面也是平行的（以后可证）．对于异面直线和的距离，也可转化为直线到平面的距离，这也是求异面直线的距离的一种方法．‎ 典型例题十 例10　如图，求证：如果一条直线和两个相交平面都平行，那么这条直线和它们的交线平行．‎ 已知：，，，求证：．‎ 分析：本题考查综合运用线面平行的判定定理和性质定理的能力．利用线面平行的性质定理，可以先证明直线分别和两平面的某些直线平行，即线面平行可得线线平行．然后再用线面平行的判定定理和性质定理来证明与平行．‎ 证明：在平面内取点，使，过和直线作平面交于．‎ ‎∵，，，‎ ‎∴．‎ 同理过作平面交于．‎ ‎∵，，，‎ ‎∴．‎ ‎∴．‎ ‎∵，，‎ ‎∴．‎ 又∵，，‎ ‎∴．‎ 又∵，‎ ‎∴．‎ 另证：如图，在直线上取点，‎ 过点和直线作平面和相交于直线，和相交于直线．‎ ‎∵，∴，‎ ‎∵，∴，‎ 但过一点只能作一条直线与另一直线平行．‎ ‎∴直线和重合．‎ 又∵，，‎ ‎∴直线、都重合于直线，‎ ‎∴．‎ 说明：“线线平行”与“线面平行”在一定条件下是可以相互转化的，这种转化的思想在立体几何中非常重要．‎ 典型例题十一 例11　正方形与正方形所在平面相交于，在、上各取一点、，且．求证：面．‎ 分析：要证线面平行，可以根据判定定理，转化为证明线线平行．关键是在平面中如何找一直线与平行．可考察过的平面与平面的交线，这样的平面位置不同，所找的交线也不同．‎ 证明一：如图，在平面内过作交于，‎ 在平面内过作交于，连结．‎ ‎∵，∴．‎ 又∵，‎ ‎∴，即． ‎ ‎∵正方形与有公共边， ‎ ‎∴．‎ ‎∵，∴．‎ ‎∴．‎ 又∵，，‎ ‎∴．‎ ‎∴四边形为平行四边形．‎ ‎∴．‎ 又∵面，‎ ‎∴面．‎ 证明二：如图，连结并延长交于，连结．‎ ‎∵，∴．‎ 又∵正方形与正方形有公共边，‎ ‎∴，‎ ‎∵，∴．‎ ‎∴．‎ ‎∴，‎ 又∵面，‎ ‎∴面．‎ 说明：从本题中我们可以看出，证线面平行的根本问题是要在平面内找一直线与已知直线平行，此时常用中位线定理、成比例线段、射影法、平行移动、补形等方法，具体用何种方法要视条件而定．此题中我们可以把“两个有公共边的正方形”这一条件改为“两个全等的矩形”，那么题中的结论是否仍然成立？‎ 典型例题十二 例12　三个平面两两相交于三条交线，证明这三条交线或平行、或相交于一点．‎ 已知：，，．‎ 求证：、、互相平行或相交于一点．‎ 分析：本题考查的是空间三直线的位置关系，我们可以先从熟悉的两条交线的位置关系入手，根据共面的两条直线平行或相交来推论三条交线的位置关系．‎ 证明：∵，，‎ ‎∴．‎ ‎∴与平行或相交．‎ ‎①若，如图 ‎∵，，∴．‎ 又∵，，∴．‎ ‎∴．‎ ‎②若与相交，如图，设，‎ ‎∴，．‎ 又∵，．‎ ‎∴，‎ 又∵，∴．‎ ‎∴直线、、交于同一点．‎ 说明：这一结论常用于求一个几何体的截面与各面交线问题，如正方体中，‎ ‎、分别是、的中点，画出点、、的平面与正方体各面的交线，并说明截面多边形是几边形？‎ 典型例题十三 例13　已知空间四边形，，是的边上的高，是的边上的中线，求证：和是异面直线．‎ 证法一：（定理法）如图 由题设条件可知点、不重合，设所在平面．‎ ‎∴和是异面直线．‎ 证法二：（反证法）‎ 若和不是异面直线，则和共面，设过、的平面为．‎ ‎(1)若、重合，则是的中点，这与题设相矛盾．‎ ‎(2)若、不重合，‎ ‎∵，，，∴．‎ ‎∵，，‎ ‎∴、、、四点共面，这与题设是空间四边形相矛盾．‎ 综上，假设不成立．‎ 故和是异面直线．‎ 说明：反证法不仅应用于有关数学问题的证明，在其他方面也有广泛的应用．‎ 首先看一个有趣的实际问题：‎ ‎“三十六口缸，九条船来装，只准装单，不准装双，你说怎么装？”‎ 对于这个问题，同学们可试验做一做．‎ 也许你在试验几次后却无法成功时，觉得这种装法的可能性是不存在的．那么你怎样才能清楚地从理论上解释这种装法是不可能呢？‎ 用反证法可以轻易地解决这个问题．假设这种装法是可行的，每条船装缸数为单数，则9个单数之和仍为单数，与36这个双数矛盾．只须两句话就解决了这个问题．‎ 典型例题十四 例14　已知、、是不在同一平面内的三条线段，、、分别是、、的中点，求证：平面和平行，也和平行．‎ 分析：欲证明平面，根据直线和平面平等的判定定理只须证明平行平面内的一条直线，由图可知，只须证明．‎ 证明：如图，连结、、、．‎ 在中，、分别是、的中点．‎ ‎∴．于是平面．‎ 同理可证，平面．‎ 说明：到目前为止，判定直线和平面平行有以下两种方法：(1)根据直线和平面平行定义；(2)根据直线和平面平行的判定定理．‎ 典型例题十五 例15　已知空间四边形，、分别是和的重心，‎ 求证：．‎ 分析：欲证线面平行，须证线线平行，即要证明与平面中的某条直线平行，根据条件，此直线为，如图．‎ 证明：取的中点．‎ ‎∵是的重心，连结，‎ 则，连结，‎ ‎∵为的重心，‎ ‎∴，‎ ‎∴在中，．‎ 又，，‎ ‎∴．‎ 说明：(1)本例中构造直线与平行，是充分借助于题目的条件：、分别是和的重心，借助于比例的性质证明，该种方法经常使用，望注意把握．‎ ‎(2)“欲证线面平行，只须证线线平行”．判定定理给我们提供了一种证明线面平等的方法．根据问题具体情况要熟练运用．‎ 典型例题十六 例16　正方体中，、分别是、的中点如下图．‎ 求证：．‎ 分析：要证明，根据线面平等的判定定理，需要在平面内找到与平行的直线，要充分借助于、为中点这一条件．‎ 证明：取的中点，连结、．‎ ‎∵为的中点，‎ ‎∴为的中位线，则，且．‎ ‎∵为的中点，‎ ‎∴且，‎ ‎∴且，‎ ‎∴四边形为平行四边形，‎ ‎∴，而，，‎ ‎∴．‎ 典型例题十七 例17　如果直线，那么直线与平面内的（　　）．‎ A．一条直线不相交　　　　B．两条相交直线不相交 ‎　　C．无数条直线不相交　　　D．任意一条直线都不相交 解：根据直线和平面平行定义，易知排除A、B．对于C，无数条直线可能是一组平行线，也可能是共点线，∴C也不正确，应排除C．‎ 与平面内任意一条直线都不相交，才能保证直线与平面平行，∴D正确．‎ ‎∴应选D．‎ 说明：本题主要考查直线与平面平行的定义．‎ 典型例题十八 例18　分别和两条异面直线平行的两条直线的位置关系是（　　）．‎ A．一定平行　　　　　　B．一定相交 C．一定异面　　　　　　D．相交或异面 解：如图中的甲图，分别与异面直线、平行的两条直线、是相交关系；‎ 如图中的乙图，分别与异面直线、平行的两条直线、是相交关系．‎ 综上，可知应选D．‎ 说明：本题主要考查有关平面、线面平行等基础知识以及空间想象能力．‎ 典型例题十九 例19　、是两条异面直线，下列结论正确的是（　　）．‎ ‎　　A．过不在、上的任一点，可作一个平面与、平行 B．过不在、上的任一点，可作一个直线与、相交 C．过不在、上的任一点，可作一个直线与、都平行 D．过可以并且只可以作一平面与平行 解：A错，若点与所确定的平面与平行时，就不能使这个平面与平行了．‎ B错，若点与所确定的平面与平等时，就不能作一条直线与，相交．‎ C错，假如这样的直线存在，根据公理4就可有，这与，异面矛盾．‎ D正确，在上任取一点A，过A点做直线，‎ 则与确定一个平面与平行，这个平面是惟一的．‎ ‎∴应选Ｄ．‎ 说明：本题主要考查异面直线、线线平行、线面平行等基本概念．‎ 典型例题二十 例20　(1)直线，，则与平面的位置关系是_____________．‎ ‎(2)是两异面直线、外的一点，过最多可作___________个平面同时与、平行．‎ 解：(1)当直线在平面外时，；当直线在平面内时，．‎ ‎∴应填：或．‎ ‎(2)因为过点分别作，的平行线只能作一条，‎ ‎（分别称，）经过，的平面也是惟一的．所以只能作一个平面；‎ 还有不能作的可能，当这个平面经过或时，这个平面就不满足条件了．‎ ‎∴应填：1．‎ 说明：考虑问题要全面，各种可能性都要想到，是解答本题的关键．‎ 典型例题二十一 例21　如图，，是的另一侧的点，，线段，，交于，，，若，，，则=___________．‎ 解：∵，．‎ ‎∴，即，‎ ‎∴．‎ 则．‎ ‎∴应填：．‎ 说明：本题是一道综合题，考查知识主要有：直线与平面平行性质定理、相似三角形、比例性质等．同时也考查了综合运用知识，分析和解决问题的能力．‎