高考数学全国卷二理科完美版 10页

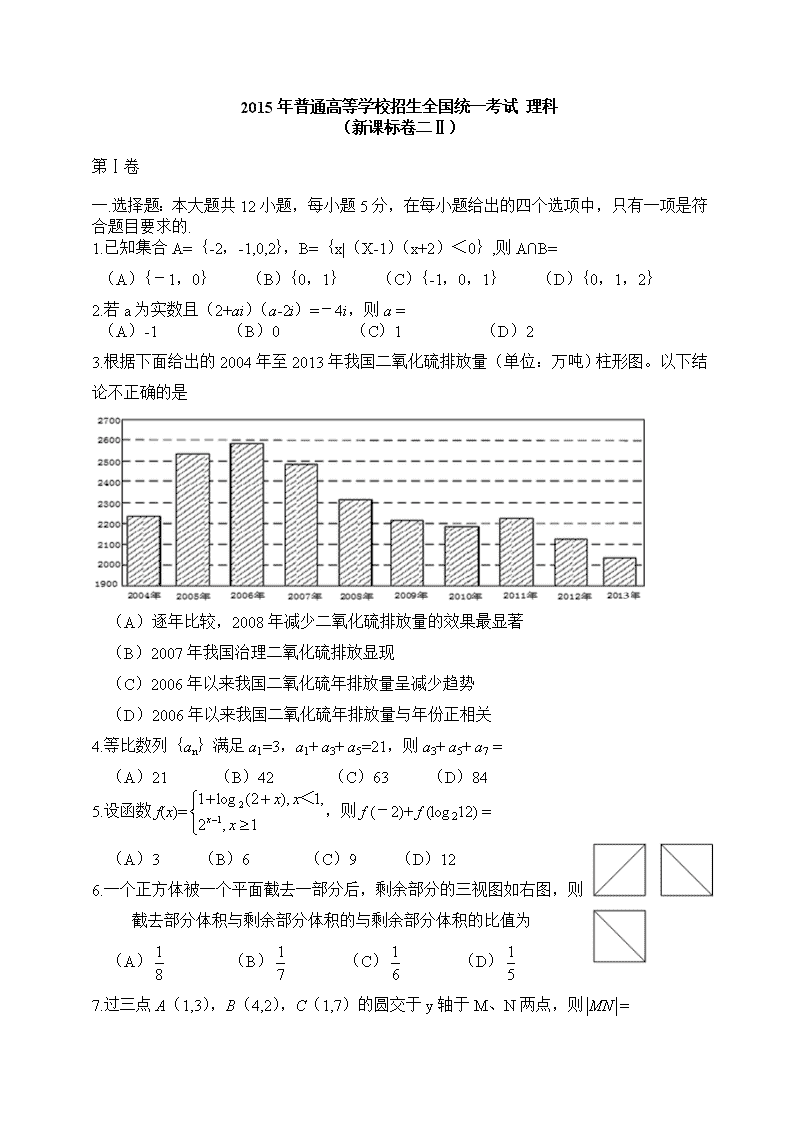
‎2015年普通高等学校招生全国统一考试 理科 ‎（新课标卷二Ⅱ）‎ 第Ⅰ卷 一.选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.已知集合A=｛-2，-1,0,2｝，B=｛x|（X-1）（x+2）＜0｝,则A∩B=‎ ‎ （A）｛－1，0｝ （B）｛0，1｝ （C）｛-1，0，1｝ （D）｛0，1，2｝‎ ‎2.若a为实数且（2+ai）（a-2i）=－4i，则a =‎ ‎ （A）-1 （B）0 （C）1 （D）2‎ 3. 根据下面给出的2004年至2013年我国二氧化硫排放量（单位：万吨）柱形图。以下结论不正确的是 ‎ （A）逐年比较，2008年减少二氧化硫排放量的效果最显著 ‎ （B）2007年我国治理二氧化硫排放显现 ‎ （C）2006年以来我国二氧化硫年排放量呈减少趋势 ‎ （D）2006年以来我国二氧化硫年排放量与年份正相关 ‎4.等比数列｛an｝满足a1=3，a1+ a3+ a5=21，则a3+ a5+ a7 =‎ ‎ （A）21 （B）42 （C）63 （D）84‎ ‎5.设函数f(x)=，则f (－2)+ f (log212) =‎ ‎ （A）3 （B）6 （C）9 （D）12‎ 6. 一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则 ‎ 截去部分体积与剩余部分体积的与剩余部分体积的比值为 ‎ （A） （B） （C） （D）‎ ‎7.过三点A（1,3），B（4,2），C（1,7）的圆交于y轴于M、N两点，则=‎ ‎ （A）2 （B）8 （C）4 （D）10‎ ‎8.右边程序抗土的算法思路源于我国古代数学名著《九章算术》‎ ‎ 中的“更相减损术”。执行该程序框图，若输入a,b分别为14,18，‎ ‎ 则输出的a=‎ ‎ （A）0 ‎ ‎ （B）2 ‎ ‎ （C）4 ‎ ‎ （D）14‎ 9. 已知A,B是球O的球面上两点，∠AOB=90,C为该球面上的动点，若三棱锥O-ABC体 ‎ 积的最大值为36，则球O的表面积为 ‎ （A）36π （B）64π （C）144π （D）256π 10. 如图，长方形ABCD的边AB=2，BC=1，O是AB的中点，点P沿着边BC，CD与 ‎ DA运动，∠BOP=x。将动点P到AB两点距离之和表示为x的函数f（x），则f（x）‎ ‎ 的图像大致为 11. 已知A，B为双曲线E的左，右顶点，点M在E上，∆ABM为等腰三角形，且顶角为 ‎ 120°，则E的离心率为 ‎ (A) (B)2 (C) (D)‎ ‎12.设函数f’(x)是奇函数f (x)(x∈R)的导函数，f（-1）=0，当x>0时，x f’(x)－f (x)＜0，则使得f (x) >0成立的x的取值范围是 ‎ (A) (－∞，－1)∪(0，1) (B) (－1，0)∪(1，＋∞) ‎ ‎ (C) (－∞，－1)∪(－1，0) (D) (0，1)∪(1，＋∞)‎ 第Ⅱ卷 ‎ 本卷包括必考题和选考题两部分.第13题~第21题为必考题，每个试题考生必须做答.第22题~第24题为选考题，考生根据要求做答。‎ 二.填空题 ‎13.设向量a，b不平行，向量λa＋b与a＋2b平行，则实数λ=________.(用数字填写答案)‎ ‎14.若x，y满足约束条件，则z= x＋y的最大值为____________..‎ ‎15.(a＋x)(1＋x)4的展开式中x的奇数次幂项的系数之和为32，则a =__________.‎ ‎16.设Sn是数列{an}的前n项和，且a1=－1，an+1=Sn Sn+1，则Sn=________.‎ 三.解答题：解答应写出文字说明，证明过程或演算步骤.‎ ‎17.（本小题满分12分）‎ ‎（17）∆ABC中，D是BC上的点，AD平分∠BAC，∆ABD是∆ADC面积的2倍。‎ ‎(Ⅰ) 求；‎ ‎(Ⅱ) 若AD=1，DC=，求BD和AC的长.‎ ‎18. 某公司为了解用户对其产品的满意度，从A，B两地区分别随机调查了20个用户，得到用户对产品的满意度评分如下：‎ A地区：62 73 81 92 95 85 74 64 53 76‎ ‎ 78 86 95 66 97 78 88 82 76 89‎ B地区：73 83 62 51 91 46 53 73 64 82‎ ‎ 93 48 65 81 74 56 54 76 65 79‎ ‎（Ⅰ）根据两组数据完成两地区用户满意度评分的茎叶图，并通过茎叶图比较两地区满意度评分的平均值及分散程度（不要求计算出具体值，得出结论即可）；‎ ‎（Ⅱ）根据用户满意度评分，将用户的满意度从低到高分为三个不等级：‎ 满意度评分 低于70分 ‎70分到89分 不低于90分 满意度等级 不满意 满意 非常满意 记时间C：“A地区用户的满意度等级高于B地区用户的满意度等级”。假设两地区用户的评价结果相互独立。根据所给数据，以事件发生的频率作为相应事件发生的概率，求C的概率 ‎19. 如图，长方体ABCD-A1B1C1D1中AB=16，BC=10，AA1=8，点E，F分别在A1B1，D1C1上，A1E=D1F。过带你E，F的平面α与此长方体的面相交，交线围成一个正方形 ‎（Ⅰ）在图中画出这个正方形（不必说出画法和理由）‎ ‎（Ⅱ）求直线AF与平面α所成角的正弦值 20. 已知椭圆C：9x2+ y2 = m2 (m>0)，直线l不过原点O且不平行于坐标轴，l与C有 ‎ 两个交点A，B，线段AB的中点为M.‎ ‎ （I）证明：直线OM的斜率与l的斜率的乘积为定值；‎ ‎ （II）若l过点(，m),延长线段OM与C交于点P，四边形OAPB能否平行四边行？‎ ‎ 若能，求此时l的斜率，若不能，说明理由.‎ ‎21. 设函数f(x)=emx＋x2－mx.‎ ‎ (Ⅰ)证明：f(x)在（－∞，0）单调递减，在（0，＋∞）单调递增；‎ ‎（Ⅱ）若对于任意x1, x2∈[-1,1],都有｜f(x1)- f(x2)｜≤e-1,求m的取值范围 ‎ 请考生在第22、23、24题中任选一题做答，如果多做，则按所做的第一题计分，做答时请写清题号.‎ ‎(22).（本小题满分10分）选修4—1：几何证明选讲 ‎ 如图，O为等腰三角形ABC内一点，圆O与ABC的底边BC交于M、N两点与底边 ‎ 上的高AD交于点G，且与AB、AC分别相切于E、F两点. ‎ ‎ （I）证明：EF平行于BC ‎ （II） 若AG等于圆O的半径，且AE=MN=,求四边形EBCF的面积。‎ ‎（23）（本小题满分10分）选修4-4：坐标系与参数方程 在直角坐标系xOy中，曲线C1:，其中0≤α＜π ，在以O 为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ=2sinθ，曲线C3：ρ=cosθ . ‎ ‎ （I）.求C2与C3交点的直角坐标 ‎ （II）.若C1与C2相交于点A，C1与C3相交于点B，求的最大值 ‎（24）（本小题满分10分）选修4-5不等式选讲 ‎ 设a、b、c、d均为正数，且a+b=c+d,证明：‎ ‎ （I）若ab＞cd ，则；‎ ‎ （II）是的充要条件.‎