高考数学新课标2文科真题及答案 10页

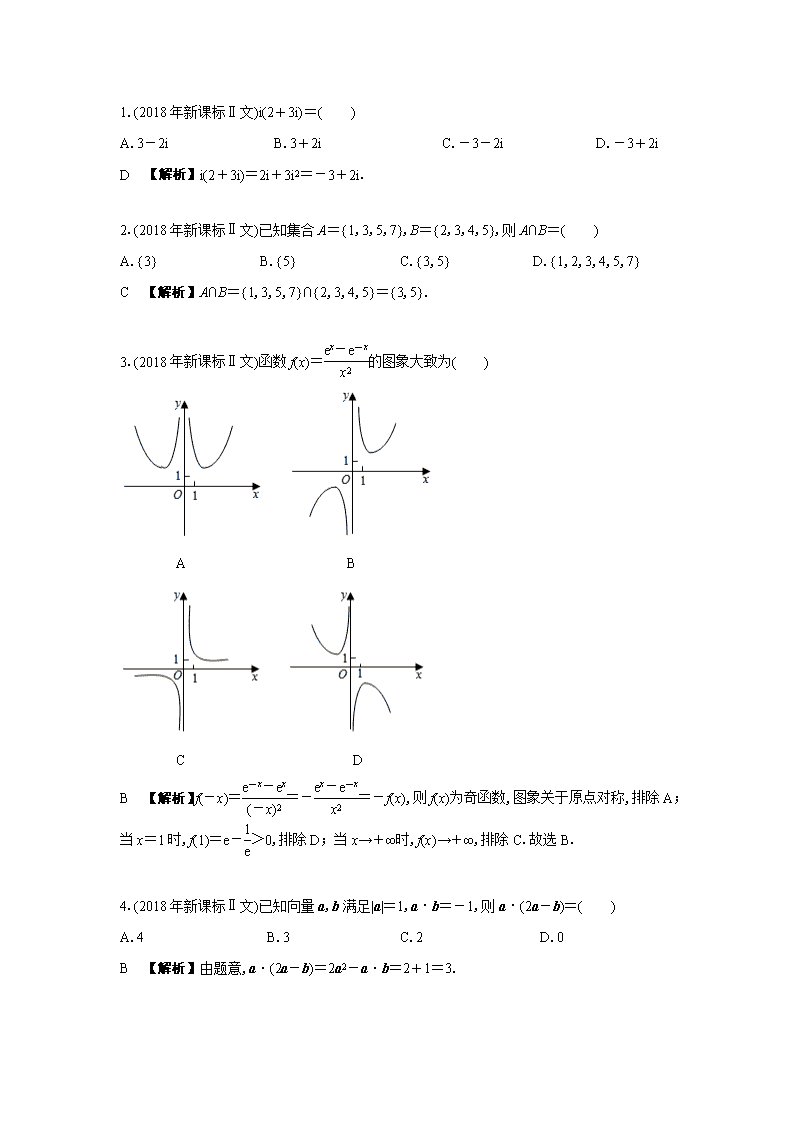
‎1.(2018年新课标Ⅱ文)i(2＋3i)＝( )‎ A.3－2i B.3＋2i C.－3－2i D.－3＋2i D 【解析】i(2＋3i)＝2i＋3i2＝－3＋2i.‎ ‎2.(2018年新课标Ⅱ文)已知集合A＝{1,3,5,7},B＝{2,3,4,5},则A∩B＝( )‎ A.{3} B.{5} C.{3,5} D.{1,2,3,4,5,7}‎ C 【解析】A∩B＝{1,3,5,7}∩{2,3,4,5}＝{3,5}.‎ ‎3.(2018年新课标Ⅱ文)函数f(x)＝的图象大致为( )‎ ‎ ‎ A B ‎ ‎ C D B 【解析】f(－x)＝＝－＝－f(x),则f(x)为奇函数,图象关于原点对称,排除A；当x＝1时,f(1)＝e－＞0,排除D；当x→＋∞时,f(x)→＋∞,排除C.故选B.‎ ‎4.(2018年新课标Ⅱ文)已知向量a,b满足|a|＝1,a·b＝－1,则a·(2a－b)＝( )‎ A.4 B.3 C.2 D.0‎ B 【解析】由题意,a·(2a－b)＝2a2－a·b＝2＋1＝3.‎ ‎5.(2018年新课标Ⅱ文)从2名男同学和3名女同学中任选2人参加社区服务,则选中的2人都是女同学的概率为( )‎ A.0.6 B.0.5 C.0.4 D.0.3‎ D 【解析】设2名男生为a,b,3名女生为A,B,C,则任选2人的种数为ab,aA,aB,aC,bA,bB,Bc,AB,AC,BC,共10种,其中全是女生为AB,AC,BC共3种,所以选中的2人都是女同学的概率p＝＝0.3.‎ ‎6.(2018年新课标Ⅱ文)双曲线－＝1(a>0,b>0)的离心率为,则其渐近线方程为( )‎ A.y＝±x B.y＝±x C.y＝±x D.y＝±x A 【解析】依题意,e＝＝,则＝＝＝＝,所以双曲线的渐近线方程为y＝±x＝±x.故选A.‎ ‎7.(2018年新课标Ⅱ文)在△ABC中,cos ＝,BC＝1,AC＝5,则AB＝( )‎ A.4 B. C. 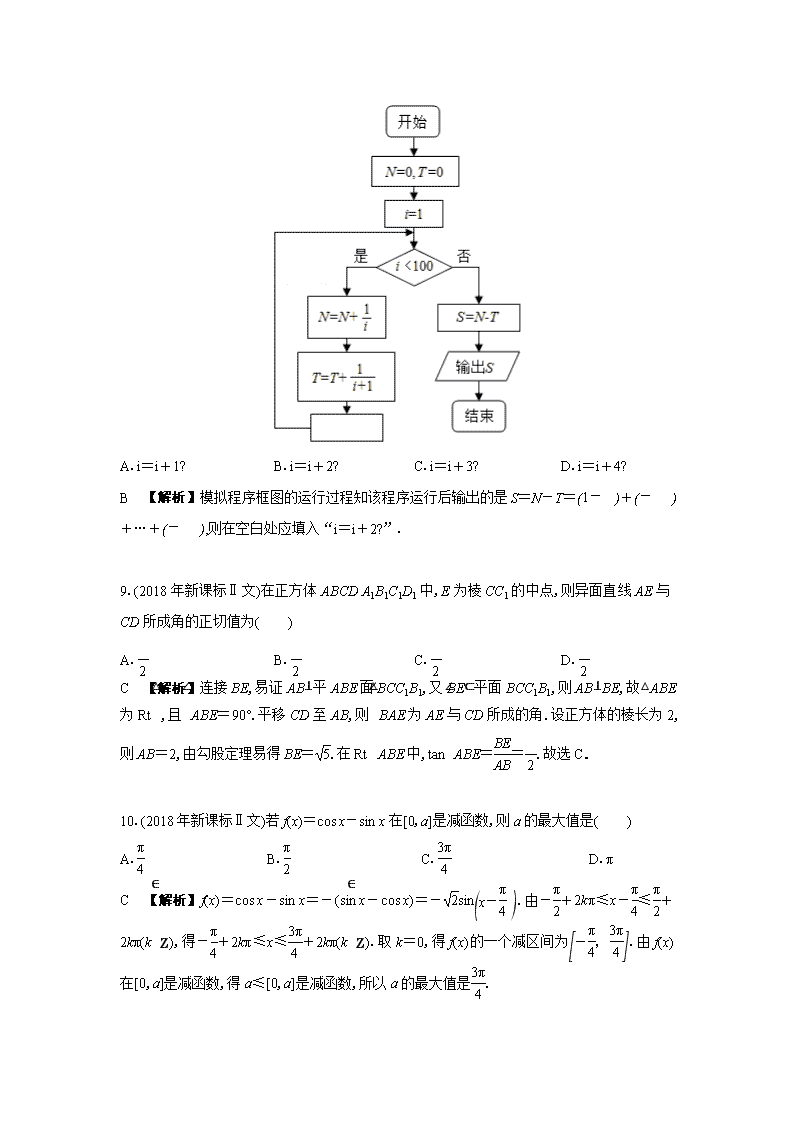D.2 A 【解析】cos C＝2×2－1＝－,由余弦定理,得AB＝ ‎＝＝4.‎ ‎8.(2018年新课标Ⅱ文)为计算S＝1－＋－＋…＋－,设计了如图的程序框图,则在空白框中应填入( )‎ A.i＝i＋1? B.i＝i＋2? C.i＝i＋3? D.i＝i＋4?‎ B 【解析】模拟程序框图的运行过程知该程序运行后输出的是S＝N－T＝＋＋…＋,则在空白处应填入“i＝i＋2?”.‎ ‎9.(2018年新课标Ⅱ文)在正方体ABCDA1B1C1D1中,E为棱CC1的中点,则异面直线AE与CD所成角的正切值为( )‎ A. B. C. D. C 【解析】连接BE,易证AB⊥平ABE面BCC1B1,又BE⊂平面BCC1B1,则AB⊥BE,故△ABE为Rt△,且∠ABE＝90°.平移CD至AB,则∠BAE为AE与CD所成的角.设正方体的棱长为2,则AB＝2,由勾股定理易得BE＝.在Rt△ABE中,tan∠ABE＝＝.故选C.‎ ‎10.(2018年新课标Ⅱ文)若f(x)＝cos x－sin x在[0,a]是减函数,则a的最大值是( )‎ A. B. C. D.π C 【解析】f(x)＝cos x－sin x＝－(sin x－cos x)＝－sin.由－＋2kπ≤x－≤＋2kπ(k∈Z),得－＋2kπ≤x≤＋2kπ(k∈Z).取k＝0,得f(x)的一个减区间为.由f(x)在[0,a]是减函数,得a≤[0,a]是减函数,所以a的最大值是.‎ ‎11.(2018年新课标Ⅱ文)已知F1,F2是椭圆C的两个焦点,P是C上的一点,若PF1⊥PF2,且∠PF2F1＝60°,则C的离心率为( )‎ A.1－ B.2－ C. D.－1‎ D 【解析】如图,在Rt△PF1F2中,|F1F2|＝2c.∵∠PF2F1＝60°,∴|PF2|＝c.由椭圆的定义,得|PF1|＋|PF2|＝2a,∴|PF1|＝2a－c.由勾股定理,得|PF1|2＋|PF2|2＝|F1F2|2,即(2a－c)2＋c2＝(2c)2,化简得＝－1±.又椭圆的离心率e∈(0,1),∴C的离心率＝＝－1.‎ ‎12.(2018年新课标Ⅱ文)已知f(x)是定义域为(－∞,＋∞)的奇函数,满足f(1－x)＝f(1＋x),若f(1)＝2,则f(1)＋f(2)＋f(3)＋…＋f(50)＝( )‎ A.－50 B.0 C.2 D.50‎ C 【解析】∵f(x)是奇函数,且f(1－x)＝f(1＋x),∴f(1－x)＝f(1＋x)＝－f(x－1),f(0)＝0,则f(x＋2)＝－f(x),则f(x＋4)＝－f(x＋2)＝f(x),即f(x)是周期为4的周期函数.∵f(1)＝2,∴f(2)＝f(0)＝0,f(3)＝f(1－2)＝f(－1)＝－f(1)＝－2,f(4)＝f(0)＝0,则f(1)＋f(2)＋f(3)＋f(4)＝2＋0－2＋0＝0,∴则f(1)＋f(2)＋f(3)＋…＋f(50)＝12[f(1)＋f(2)＋f(3)＋f(4)]＋f(49)＋f(50)＝f(1)＋f(2)＝2＋0＝2.‎ ‎13.(2018年新课标Ⅱ文)曲线y＝2ln x在点(1,0)处的切线方程为________.‎ y＝2x－2 【解析】∵y＝2ln x,∴y′＝.当x＝1时,y′＝2,∴曲线y＝2ln x在点(1,0)处的切线方程为y－0＝2(x－1),即y＝2x－2.‎ ‎14.(2018年新课标Ⅱ文)若x,y满足约束条件则z＝x＋y的最大值为________.‎ ‎9 【解析】作出可行域如图.z＝x＋y可化为y＝－x＋z.当直线y＝－x＋z过A(5,4)时,z取得最大值,最大值为z＝5＋4＝9.‎ ‎15.(2018年新课标Ⅱ文)已知tan＝,则tan α＝________.‎ 【解析】∵tan＝tan＝,∴tan α＝tan＝＝＝.‎ ‎16.(2018年新课标Ⅱ文)已知圆锥的顶点为S,母线SA,SB互相垂直,SA与圆锥底面所成角为30°.若△SAB的面积为8,则该圆锥的体积为________.‎ ‎8π 【解析】依题意可得△SAB的面积＝SA2＝8,解得SA＝4.由SA与圆锥底面所成角为30°,可得圆锥的底面半径为2,圆锥的高为2,所以该圆锥的体积V＝π·(2)2·2＝8π.‎ ‎17.(2018年新课标Ⅱ文)记Sn为等差数列{an}的前n项和,已知a1＝－7,S3＝－15.‎ ‎（1）求{an}的通项公式；‎ ‎（2）求Sn,并求Sn的最小值.‎ ‎【解析】（1）设等差数列{an}的公差为d.‎ S3＝3a1＋3d＝3×(－7)＋3d＝－15,解得d＝2.‎ ‎∴an＝a1＋(n－1)d＝－7＋2(n－1)＝2n－9.‎ ‎（2）Sn＝＝＝n2－8n.‎ ‎∵Sn＝n2－8n＝(n－4)2－16,‎ ‎∴当n＝4时,Sn有最小值为－16.‎ ‎18.(2018年新课标Ⅱ文)如图是某地区2000年至2016年环境基础设施投资额y(单位:亿元)‎ 的折线图.‎ 为了预测该地区2018年的环境基础设施投资额,建立了y与时间变量t的两个线性回归模型.根据2000年至2016年的数据(时间变量t的值依次为1,2,…,17)建立模型①:＝－30.4＋13.5t；根据2010年至2016年的数据(时间变量t的值依次为1,2,…,7)建立模型②:＝99＋17.5t.‎ ‎（1）分别利用这两个模型,求该地区2018年的环境基础设施投资额的预测值；‎ ‎（2）你认为用哪个模型得到的预测值更可靠?并说明理由.‎ ‎【解析】（1）对于模型①,当t＝19时,＝－30.4＋13.5×19＝226.1,即该地区2018年的环境基础设施投资额的预测值是226.1亿元.‎ 对于模型②,当t＝9时,＝99＋17.5×9＝256.5,即该地区2018年的环境基础设施投资额的预测值是256.5亿元.‎ ‎（2）模型②得到的预测值更可靠.‎ ‎∵从总体数据看,该地区从2000年到2016年的环境基础设施投资额是逐年上升的,‎ 而从2000年到2009年间递增的幅度较小些,从2010年到2016年间递增的幅度较大些,‎ ‎∴利用模型②的预测值更可靠些.‎ ‎19.(2018年新课标Ⅱ文)如图,在三棱锥PABC中,AB＝BC＝2,PA＝PB＝PC＝AC＝4,O为AC的中点.‎ ‎（1）求证:PO⊥平面ABC；‎ ‎（2）若点M在棱BC上,且MC＝2MB,求点C到平面POM的距离.‎ ‎【解析】（1）证明:∵AB＝BC＝2,AC＝4,∴AB2＋BC2＝AC2,即△ABC是直角三角形.‎ 又O为AC的中点,∴OA＝OB＝OC.‎ ‎∵PA＝PB＝PC,∴△POA≌△POB≌△POC.‎ ‎∴∠POA＝∠POB＝∠POC＝90°.‎ ‎∴PO⊥AC,PO⊥OB,OB∩AC＝0,∴PO⊥平面ABC.‎ ‎（2）由（1）得PO⊥平面ABC,PO＝＝2.‎ 在△COM中,OM＝＝.‎ S△POM＝·PO·OM＝,‎ S△COM＝×S△ABC＝.‎ 设点C到平面POM的距离为d.‎ 由VPOMC＝VCPOM,得S△POM·d＝S△COM·PO,解得d＝.‎ ‎∴点C到平面POM的距离为.‎ ‎20.(2018年新课标Ⅱ文)设抛物线C:y2＝4x的焦点为F,过F且斜率为k(k＞0)的直线l与C交于A,B两点,|AB|＝8.‎ ‎（1）求l的方程；‎ ‎（2）求过点A,B且与C的准线相切的圆的方程.‎ ‎【解析】（1）抛物线C的焦点为F(1,0).‎ 当直线的斜率不存在时,|AB|＝4,不合题意.‎ 设直线AB的方程为y＝k(x－1),A(x1,y1),B(x2,y2).‎ 联立消去y,得k2x2－2(k2＋2)x＋k2＝0,‎ ‎∴x1＋x2＝,x1x2＝1.‎ 由|AB|＝x1＋x2＋p＝＋2＝8,解得k＝1.‎ ‎∴直线l的方程y＝x－1.‎ ‎（2）由（1）得AB的中点坐标为D(3,2),‎ 则直线AB的垂直平分线方程为y－2＝－(x－3),即y＝－x＋5.‎ 设所求圆的圆心坐标为(x0,y0),则解得或 ‎∴所求圆的方程为(x－3)2＋(y－2)2＝16或(x－11)2＋(y＋6)2＝144.‎ ‎　‎ ‎21.(2018年新课标Ⅱ文)已知函数f(x)＝x3－a(x2＋x＋1).‎ ‎（1）若a＝3,求f(x)的单调区间；‎ ‎（2）求证:f(x)只有一个零点.‎ ‎【解析】（1）当a＝3时,f(x)＝x3－3(x2＋x＋1),∴f′(x)＝x2－6x－3.‎ 令f′(x)＝0,得x＝3±2.‎ 当x∈(－∞,3－2),(3＋2,＋∞)时,f′(x)＞0,f(x)单调递增；‎ 当x∈(3－2,3＋2)时,f′(x)＜0,f(x)单调递减.‎ 综上,f(x)在(－∞,3－2),(3＋2,＋∞)上单调递增,在(3－2,3＋2)上单调递减.‎ ‎（2）证明:∵x2＋x＋1＝2＋＞0,∴f(x)＝0等价于－a＝0.‎ 令g(x)＝－a,则g′(x)＝≥0,‎ 仅当x＝0时,g′(x)＝0,∴g(x)在R上是增函数.‎ g(x)至多有一个零点,从而f(x)至多有一个零点.‎ 又∵f(3a－1)＝－6a2＋2a－＝－62－＜0,f(3a＋1)＞0,‎ ‎∴f(x)有一个零点.‎ 综上,f(x)只有一个零点.‎ ‎22.(2018年新课标Ⅱ文)在直角坐标系xOy中,曲线C的参数方程为(θ为参数),直线l的参数方程为(t为参数).‎ ‎（1）求C和l的直角坐标方程；‎ ‎（2）若曲线C截直线l所得线段的中点坐标为(1,2),求l的斜率.‎ ‎【解析】（1）曲线C的参数方程为(θ为参数),‎ 转换为直角坐标方程为＋＝1.‎ 直线l的参数方程为(t为参数),‎ 转换为直角坐标方程为xsin α－ycos α＋2cos α－sin α＝0.‎ ‎（2）把直线的参数方程代入椭圆的方程,‎ 整理得(4cos2α＋sin2α)t2＋(8cos α＋4sin α)t－8＝0,则t1＋t2＝－.‎ 由于(1,2)为中点坐标,∴＝0,‎ 则8cos α＋4sin α＝0,解得tan α＝－2.‎ ‎∴直线l的斜率为－2.‎ ‎23.(2018年新课标Ⅱ文)设函数f(x)＝5－|x＋a|－|x－2|.‎ ‎（1）当a＝1时,求不等式f(x)≥0的解集；‎ ‎（2）若f(x)≤1,求a的取值范围.‎ ‎【解析】（1）当a＝1时,f(x)＝5－|x＋a|－|x－2|＝ 当x≤－1时,f(x)＝2x＋4≥0,解得－2≤x≤1；‎ 当－1＜x＜2时,f(x)＝2≥0恒成立,即－1＜x＜2；‎ 当x≥2时,f(x)＝－2x＋6≥0,解得2≤x≤3.‎ 综上,不等式f(x)≥0的解集为[－2,3].‎ ‎（2）∵f(x)≤1,∴5－|x＋a|－|x－2|≤1.‎ ‎∴|x＋a|＋|x－2|≥4.‎ ‎∴|x＋a|＋|x－2|＝|x＋a|＋|2－x|≥|x＋a＋2－x|＝|a＋2|.‎ ‎∴|a＋2|≥4,解得a≤－6或a≥2.‎ ‎∴a的取值范围(－∞,－6]∪[2,＋∞).‎