高考物理24题专练运动学问题分析 7页

运动学问题 一、运动图像类 ‎1.甲、乙两质点在同一时刻、从同一地点沿同一方向做直线运动。质点甲做初速度为零，加速度大小为a1的匀加速直线运动。质点乙做初速度为v0，加速度大小为a2的匀减速直线运动至速度减为零后保持静止。甲、乙两质点在运动过程中的位置x——速度v图象如图所示，虚线与对应的坐标轴垂直。 ‎ ‎（1）在x—v图象中，图线a表示哪个质点的运动？质点乙的初速度是多少？‎ ‎（2）求质点甲、乙的加速度大小a1、a2。‎ 解：(1)设运动过程中甲、乙的速度分别为v1、v2，根据速度与位移关系有：‎ ‎ 得： （1）‎ 可知其图象应为抛物线，且开口向上，故图线a表示质点甲的运动 （3分）‎ ‎ 得： （2）‎ 可知其图象应为抛物线，且开口向下，故图线b表示质点乙的运动，且当v2=v0时，x2=0，从图象可知：‎ v0=4m/s （3） （3分）‎ ‎(2)由图象交点可知，v1=v2时两质点的位移相同，且x=2m，有：‎ ‎，，解得：‎ ‎，a1+a2=4m/s2 （4） （2分）‎ 另据图象可知当v1=6m/s，v2=2m/s时，两质点的位移x′相同，有：‎ ‎，，解得：a1=3a2 （5） ‎ 联立（4）（5）可得：a1=3m/s2，a2=1m/s2 （6） ‎ 二、追击刹车模型 求解追及相遇问题的思路和技巧 ‎(1)基本思路 ‎(2)求解追及相遇问题的“三点技巧”‎ ‎1.滑雪度假村某段雪地赛道可等效为长L=‎36m，倾角为θ=37o的斜坡。已知滑道的积雪与不同滑板之间的动摩擦因数不同，现假定甲先滑下时滑板与赛道的动摩擦因数μ1=0.5，乙后滑时滑板与赛道的动摩擦因数为μ2=0.25，g取‎10m/s2.已知甲和乙均可看作质点，且滑行方向平行，相遇时不会相撞。求：‎ ‎（1）甲从坡顶由静止自由滑下时到达坡底的速度大小 ‎（2）若乙比甲晚出发Δt=1s，为追上甲，有人从后面给乙一个瞬时作用使乙获得初速度V0=1m/s,通过计算分析乙能否在甲到达坡底前追上甲；若能追上求出两者在追上前相距的最远距离，若不能追上求出两者到达坡底的时间差。‎ 解：（1）对甲运动，由牛顿运动定律：m1gsinθ－μ1m1gcosθ=m1a甲 a甲=2m/s2 (2分)‎ 由2a甲L=v12 (2分) 得：v1=12m/s (1分)‎ ‎（2）甲到达坡底的时间t甲==6s (1分)‎ 对乙：a乙=gsinθ－gcosθ=4m/s2 (1分) 设到达坡底时间为t乙 L=v0t乙＋a乙t乙2 得 t乙=4s (1分)‎ t乙＋△t＜t甲 故可以追上 (1分)‎ 设甲出发后经t1，乙与甲达到共同速度v，则:‎ V= a甲t1= v0＋a乙(t1－△t) 解得：t1=1.5s (2分)‎ X甲= a甲t12=m (1分) X乙= v0(t1－△t)＋a乙(t1－△t)2=1m (1分)‎ ‎∴ △x= X甲－X乙=1.25m (1分)‎ ‎2.雾霾天气会对行车安全造成很大的影响，因此在行车时司机应打开汽车的前雾灯和尾部双闪灯，以保证行车安全。若在某公路上，有一货车以‎10 m/s的速度缓慢行驶，后面的一辆小轿车由于雾霾的影响，司机只有到达距离该货车‎30 m远的地方才能看到该货车尾部双闪灯发出的光，若该司机看到双闪灯光后立即采取刹车措施，其反应时间为0.5 s，小轿车制动后减速的最大加速度为‎2 m/s2，若要避免两车相撞，小轿车行驶的速度最大不能超过多少？‎ ‎14．解析　小轿车与货车不相撞的临界条件是：小轿车追上货车时小轿车的速度正好减小到‎10 m/s。‎ 设货车匀速行驶的速度大小为v1，小轿车刹车时的速度大小为v2，小轿车司机发现货车时距货车的距离为s，小轿车减速时的加速度大小为a，小轿车追上货车所用的时间为t，司机的反应时间为Δt。则有：v2－a(t－Δt)＝v1，‎ v2Δt＋＝s＋v1t，‎ 联立并代入数据可解得：v2＝20 m/s，‎ 因此，要避免两车相撞，小轿车行驶的最大速度不能超过20 m/s。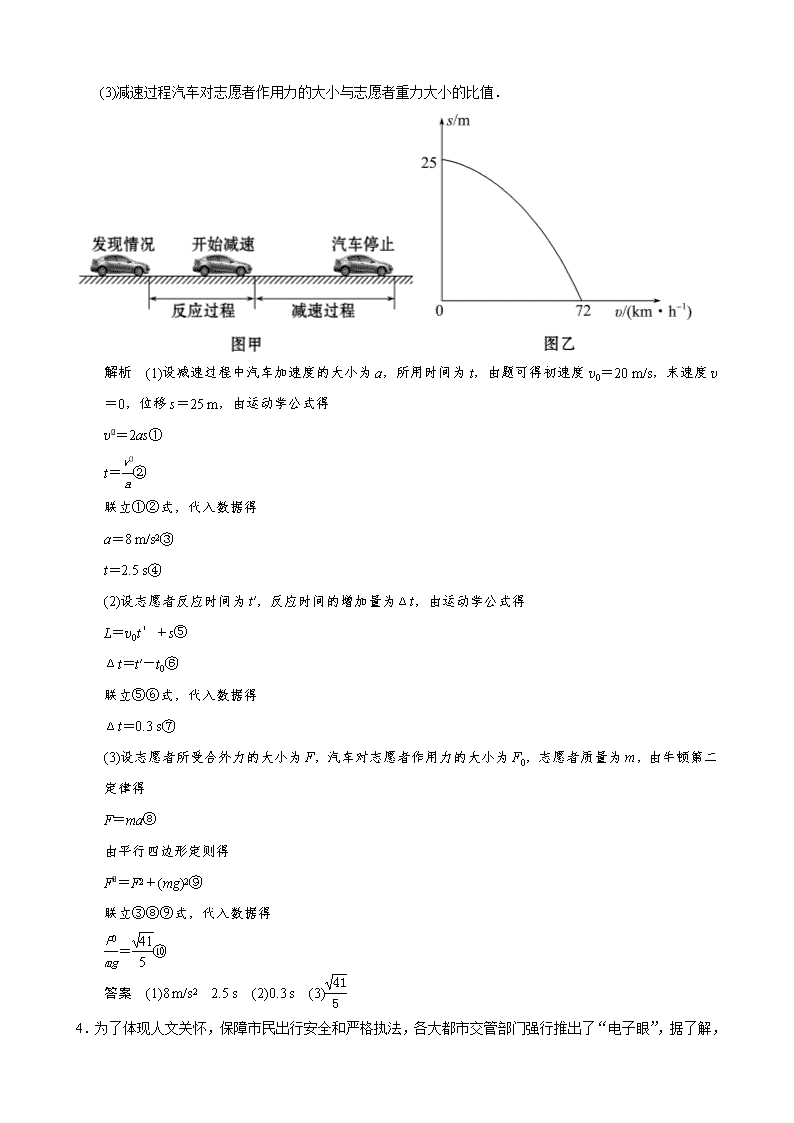‎ ‎3.研究表明，一般人的刹车反应时间(即图甲中“反应过程”所用时间)t0＝0.4 s，但饮酒会导致反应时间延长．在某次试验中，志愿者少量饮酒后驾车以v0＝72 km/h的速度在试验场的水平路面上匀速行驶，从发现情况到汽车停止，行驶距离L＝39 m．减速过程中汽车位移s与速度v的关系曲线如图乙所示．此过程可视为匀变速直线运动．取重力加速度的大小g＝10 m/s2.求：‎ ‎(1)减速过程汽车加速度的大小及所用时间；‎ ‎(2)饮酒使志愿者的反应时间比一般人增加了多少；‎ ‎(3)减速过程汽车对志愿者作用力的大小与志愿者重力大小的比值．‎ 解析　(1)设减速过程中汽车加速度的大小为a，所用时间为t，由题可得初速度v0＝20 m/s，末速度v＝0，位移s＝25 m，由运动学公式得 v＝2as①‎ t＝②‎ 联立①②式，代入数据得 a＝8 m/s2③‎ t＝2.5 s④‎ ‎(2)设志愿者反应时间为t′，反应时间的增加量为Δt，由运动学公式得 L＝v0t′＋s⑤‎ Δt＝t′－t0⑥‎ 联立⑤⑥式，代入数据得 Δt＝0.3 s⑦‎ ‎(3)设志愿者所受合外力的大小为F，汽车对志愿者作用力的大小为F0，志愿者质量为m，由牛顿第二定律得 F＝ma⑧‎ 由平行四边形定则得 F＝F2＋(mg)2⑨‎ 联立③⑧⑨式，代入数据得 ＝⑩‎ 答案　(1)8 m/s2　2.5 s　(2)0.3 s　(3) ‎4．为了体现人文关怀，保障市民出行安全和严格执法，各大都市交管部门强行推出了“电子眼”，据了解，‎ 在城区内全方位装上“电子眼”后，机动车擅自闯红灯的记录大幅度减少，因闯红灯引发的交通事故也从过去的5%下降到1%.现有甲、乙两辆汽车正沿同一平直马路同向匀速行驶，甲车在前，乙车在后，它们行驶的速度均为10 m/s.当两车快要到一十字路口时，甲车司机看到绿灯已转换成了黄灯，于是紧急刹车(反应时间忽略不计)，乙车司机为了避免与甲车相撞也紧急刹车，但乙车司机反应较慢(反应时间为0.5s)．已知甲车紧急刹车时制动力为车重的0.4倍，乙车紧急刹车时制动力为车重的0.5倍．g取10 m/s2.求；‎ ‎(1)若甲司机看到黄灯时车头距警戒线15 m，他采取上述措施能否避免闯红灯？‎ ‎(2)为保证两车在紧急刹车过程中不相撞，甲、乙两车行驶过程中应保持多大距离？‎ 解析　(1)根据牛顿第二定律可得 甲车紧急刹车的加速度大小为a1＝＝＝4 m/s2；‎ 乙车紧急刹车的加速度大小为a2＝＝＝5 m/s2；‎ 甲车停下来所需时间t1＝＝ s＝2.5 s 这段时间滑行距离s＝＝ m＝12.5 m s＝12.5 m＜15 m，甲车司机能避免闯红灯．‎ ‎(2)设甲、乙两车行驶过程中至少应保持的距离为s0，在乙车刹车的t2时间两车恰好不相撞，则有：‎ v0－a1(t2＋0.5)＝v0－a2t2‎ v0×0.5＋v0t2－a2t＝v0(t2＋0.5)－a1(t2＋0.5)2＋s0‎ 代入数据联立方程解得：t2＝2 s　s0＝2.5 m 答案　(1)能　(2)‎‎2.5 m ‎5.(2014·新课标全国Ⅰ，24，12分)(难度★★★★)公路上行驶的两汽车之间应保持一定的安全距离．当前车突然停止时，后车司机可以采取刹车措施，使汽车在安全距离内停下而不会与前车相碰．通常情况下，人的反应时间和汽车系统的反应时间之和为1 s，当汽车在晴天干燥沥青路面上以108 km/h的速度匀速行驶时，安全距离为120 m．设雨天时汽车轮胎与沥青路面间的动摩擦因数为晴天时的2/5，若要求安全距离仍为120 m，求汽车在雨天安全行驶的最大速度．‎ 解析　设路面干燥时，汽车与地面间的动摩擦因数为μ0，刹车时汽车的加速度大小为a0，安全距离为s，反应时间为t0，由牛顿第二定律和运动学公式得 μ0mg＝ma0①‎ s＝v0t0＋②‎ 式中，m和v0分别为汽车的质量和刹车前的速度．‎ 设在雨天行驶时，汽车与地面间的动摩擦因数为μ，依题意有 μ＝μ0③‎ 设在雨天行驶时汽车刹车的加速度大小为a，安全行驶的最大速度为v，由牛顿第二定律和运动学公式得 μmg＝ma④‎ s＝v-t0＋⑤‎ 联立①②③④⑤式并代入题给数据得 v＝20 m/s(‎72 km/h)⑥‎ 答案　20 m/s(‎72 km/h)‎ 三、其他类型 ‎1.在游乐场中，有种大型游乐机叫“跳楼机”．参加的游客被安全带固定在座椅上，由电动机将座椅提升到某一高处，然后由静止释放．座椅沿光滑杆自由下落一段高度后开始受到压缩空气提供的恒定阻力，下落36m后速度刚好减小到零，下落的总时间是6.0 s．求：(g取10 m/s2)‎ ‎(1)座椅被释放后，下落过程中速度的最大值vm；‎ ‎(2)座椅被释放后，自由下落的距离s1；‎ ‎(3)有一游客质量为60 kg，在下降过程中，座椅对该游客支持力功率的最大值Pm.‎ 解析　(1)vm＝＝ m/s＝12 m/s.‎ ‎(2)自由下落的距离s1＝＝ m＝7.2 m ‎(3)减速下落的距离s2＝s－s1＝(36－7.2)m＝28.8 m 减速下落时的加速度 a2＝＝－ m/s2≈－2.5 m/s2‎ ‎(说明：正负均可)‎ 由ma2＝mg－FN可解得FN＝mg－ma2＝60×12.5 N＝750 N 支持力的功率最大值Pm＝FNvm＝750×12 W＝9 000 W ‎2. 如图所示，这是在高速公路上用超声波测速仪测量车速的示意图，测速仪B发出并接收超声波脉冲信号，根据发出和接收到的信号的时间差，测出被测物体的速度．设小车向右运动先后经过P、Q两点，小车经P点时，B发出的第一个超声波脉冲被小车反射，被B接收，B从发射到接收历时t1=0.30s，小车经Q点时，B发射并接收第二个超声波脉冲历时t2=0.40s，相邻两次发射超声波脉冲的时间间隔△t=1.0s，超声波在空气中传播的速度v=340m/s，若汽车是匀速行驶的，求小车先后两次反射超声波脉冲时间内的位移△x和汽车的速度． ‎ ‎3. 如图是在高速公路上用超声波测速仪测量车速的的示意图，测速仪发出并接收超声波脉冲信号，根据发出和接收到的信号间的时间差，测出被测物体的速度。在下图中是测速仪发出的超声波信号， 分别是由汽车反射回来的信号。设测速仪匀速扫描，之间的时间间隔，超声波在空气中的传播速度是，若汽车是匀速行驶的，求： （1）汽车在接收到两个信号之间的时间内前进的距离?  （2）汽车的速度是多少？‎ ‎①P1、P2间的刻度值为30个格，时间长为1秒， 发出超声波信号P1到接受到反射信号n1间是12个格，则时间为t1=12×=0.4s， 此时超声波前进的距离S1=vt1=×340m/s×0.4s=68m； ②发出超声波信号P2到接受到反射信号n2的时间为t2=9×=0.3s， 此时汽车行驶的距离S2=vt2=×340m/s×0.3s=51m； ③所以汽车接收到P1、P2两个信号之间的时间内前进的距离为△S=S1-S2=68m-51m=17m． ④汽车运行17m的时间为汽车接收到P1、P2两个信号的时刻应分别对应于图中P1n1的中点和P2n2的中点， 其间有28.5小格，即汽车接收到P1、P2两个信号的时间间隔为n1与n2两个信号之间的间隔，即t=28.5×=0.95s； ‎ ‎∴汽车的行驶速度v===17.9m/s