北京高考数学全真模拟试题目一理新人民教育出版 10页

‎2014高考全真模拟卷（一）‎ 数学（理科）试卷 第I卷 选择题(共40分)‎ 一、选择题（本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只 有一项是符合题目要求的）‎ ‎1.　已知复数，则（ ） ‎ A． B． C． D． ‎ ‎2. 已知函数的定义域为M，g(x)=的定义域为N，则M∩N=（ ）‎ ‎ Ａ． Ｂ． Ｃ． Ｄ．‎ ‎3 中，，，，则（ ）‎ ‎ B． C． D．或 ‎4. 如右图，一个空间几何体的主视图和左视图都是边长为1的正三角形，俯视图是一个圆，那么几何体的侧面积为（ ）‎ ‎ A. B． ‎ C． D．‎ ‎5.设向量与的夹角为，=（2，1），3+=（5，4），则=（ ） ‎ ‎ A. B． C． D．‎ ‎6. 若变量满足则的最大值是（ ）‎ A．90 B．‎80 ‎C．70 D．40‎ ‎7．如图，过抛物线的焦点F的直线l交抛物线于点A、B，交其准线于点 C，若，则此抛物线的方程为（ ）‎ ‎ A． B．‎ ‎ C． D． ‎ ‎8．设奇函数上是增函数，且对所有的都成立，当时，则t的取值范围是 （ ）‎ ‎ A． B．‎ C． D．‎ 第Ⅱ卷（非选择题 共110分）‎ 二、填空题：本大题共6小题，每小题5分，共30分.把答案填在题中横线上.‎ ‎9.的展开式中的常数项是 （用数字作答）‎ ‎10. 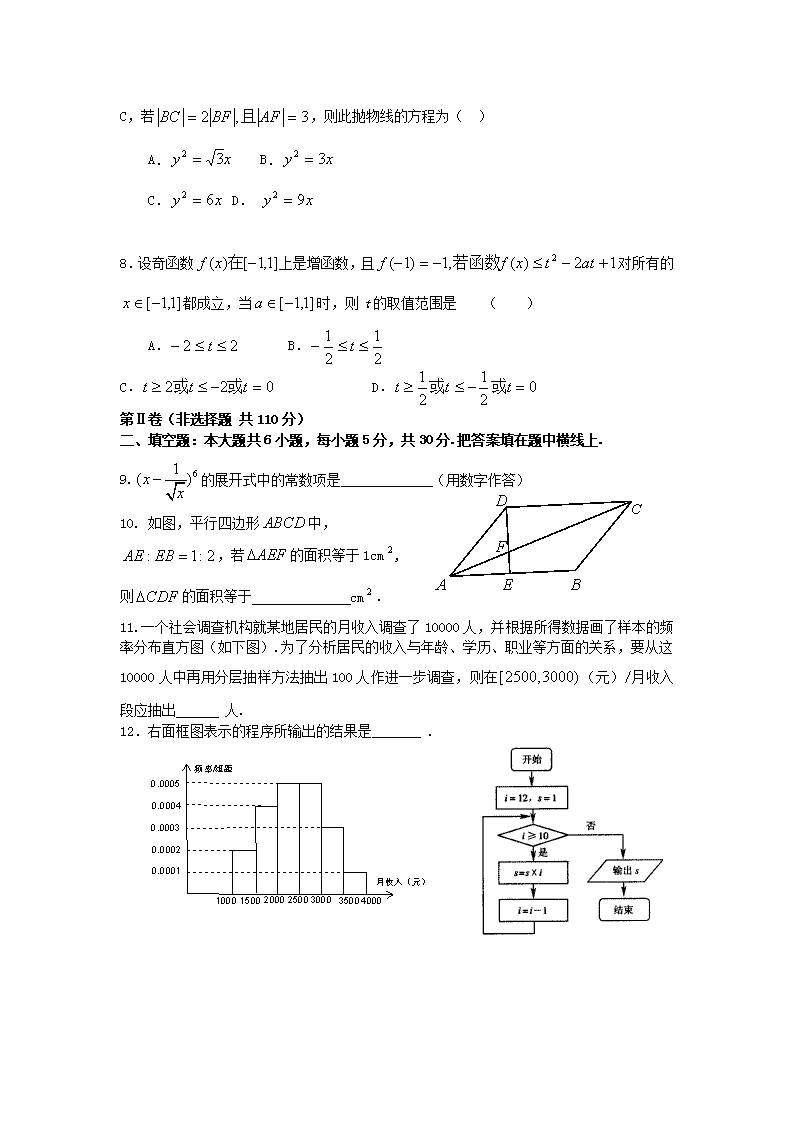如图，平行四边形中，‎ ‎，若的面积等于‎1cm,‎ 则的面积等于 cm．‎ ‎11.一个社会调查机构就某地居民的月收入调查了10000人，并根据所得数据画了样本的频率分布直方图（如下图）.为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10000人中再用分层抽样方法抽出100人作进一步调查，则在（元）/月收入段应抽出 人.‎ ‎12．右面框图表示的程序所输出的结果是_______ . ‎ ‎ ‎ ‎13. 在平面直角坐标系xOy 中，直线的参数方程为（参数t∈R），圆C的参数方程为（参数），则圆C的圆心坐标为_______，圆心到直线的距离为______.‎ ‎14．给出以下几个命题：‎ ‎ ①由曲线y=x2与直线y=2x围成的封闭区域的面积为.‎ ‎ ②已知点A是定圆C上的一个定点，线段AB为圆的动弦，若，‎ O为坐标原点，则动点P的轨迹为圆；‎ ‎ ③把5本不同的书分给4个人，每人至少1本，则不同的分法种数为A54·A41=480种.‎ ‎ ④若直线l//平面α，直线l⊥直线m，直线平面β，则β⊥α，其中，正确的命题有 . （将所有正确命题的序号都填在横线上）‎ ‎ 三、解答题：本大题共6小题，共计80分，解答应写出文字说明、证明过程或推演步骤.‎ ‎15. （本题满分12分）‎ 已知函数 ‎（Ⅰ）求函数的最小正周期和图象的对称轴方程 ‎（Ⅱ）求函数在区间上的值域.‎ ‎16（本题满分13分）‎ ‎ 如图，棱锥P—ABCD的底面ABCD是矩形，PA⊥平面ABCD，PA=AD=2，BD=.‎ ‎（Ⅰ）求证：；‎ ‎（Ⅱ）求二面角的余弦值；‎ D P A B C ‎（III）在线段上是否存在一点,使与平面所成的角的正弦值为，若存在，指出点的位置，若不存在，说明理由.‎ ‎17. （本小题满分13分）‎ 甲乙两队参加奥运知识竞赛，每队3人，每人回答一个问题，答对者为本队赢得一分，答错得零分.假设甲队中每人答对的概率均为，乙队中3人答对的概率分别为且各人正确与否相互之间没有影响.用ξ表示甲队的总得分.‎ ‎（Ⅰ）求随机变量ξ分布列和数学期望； ‎ ‎(Ⅱ)用A表示“甲、乙两个队总得分之和等于‎3”‎这一事件，用B表示“甲队总得分大于乙队总得分”这一事件，求P(AB).‎ ‎18．（本小题满分14分）‎ 已知是函数的一个极值点.‎ ‎（Ⅰ）求；‎ ‎（Ⅱ）求函数的单调区间；‎ ‎（Ⅲ）若直线与函数的图象有3个交点，求的取值范围. ‎ ‎19. (本题满分14分)‎ 在直角坐标系xOy中，椭圆C1：的左、右焦点分别为F1、F2.其中F2也是抛物线C2：的焦点，点M为C1与C2在第一象限的交点，且.‎ ‎（1）求C1的方程；‎ ‎（2）平面上的点N满足，直线l∥MN，且与C1交于A、B两点，若·=0，求直线l的方程.‎ ‎20. (本题满分14分)‎ 已知数列中，，，其前项和满足（，）．‎ ‎（1）求数列的通项公式；‎ ‎（2）设为非零整数，），试确定的值，使得对任意，都有成立．‎ ‎2014北京高中数学（理科）模拟答案及评分标准 一.选择题(共40分)‎ 题号 ‎ 1‎ ‎ 2‎ ‎ 3‎ ‎ 4‎ ‎ 5‎ ‎ 6‎ ‎ 7‎ ‎ 8‎ 答案 ‎ D C ‎ ‎ B ‎ A ‎ D ‎ C ‎ B ‎ C 二.填空题(共30分)‎ ‎9．15 10. 9 11. 25 12. 1320 13.（0，2）； 14. ①② ‎ 三.解答题 ‎15．解：（I）‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ………………………………………… 4分 ‎ .……………………………………………6分 由 函数图象的对称轴方程为 .…………… 8分 ‎（II） ………………………………… 9分 因为在区间上单调递增，在区间上单调递减，‎ 所以 当时，取最大值 1.‎ 又 ，当时，取得最小值.‎ y z D P A B C x 所以 函数 在区间上的值域为.……………………………12分 ‎16.（Ⅰ）在Rt△BAD中，AD=2，BD=， ‎ ‎∴AB=2，ABCD为正方形，因此BD⊥AC. ‎ ‎∵PA⊥平面ABCD, ‎ ‎∴BD⊥PA .‎ ‎∵,‎ ‎∴.………………………… 4分 得. ……………………………………………………………5分 ‎（Ⅱ）如图建立空间直角坐标系,则，，，‎ ‎，，‎ 易求平面的法向量为,‎ 平面的法向量为 …………………………………………… 7分 ‎， ‎ 二面角的余弦值. …………………………………………… 9分 ‎（III）因为在上，所以可设， ‎ 又,‎ ‎ ‎ ‎,.……………………… 10分 由（Ⅱ）可知平面的法向量为，‎ 所以设与平面所成的角为，则有：‎ ‎…………………………………… 11分 所以有，，， ………12分 所以存在且. ……………………………………………………………13分 ‎17．（I）由题意知，的可能取值为且 所以的分布列为 ‎………………………………………………… 5分 的数学期望为…………………………7分 ‎（II）用表示“甲得2分乙得1分”这一事件，用表示“甲得3分乙得0分”这一事件，互斥.‎ ‎…………9分 ‎………………………………………………………………………… 11分 ‎ ………………………… 13分 ‎18.解：（Ⅰ）因为………………………………………… 2分 ‎ 所以 ‎ 因此. ………………………………………………………………… 4分 ‎（Ⅱ）由（Ⅰ）知，‎ ‎ ‎ ‎ .………………………………………………………… 6分 当时，;‎ 当时，.‎ 所以的单调增区间是;‎ 的单调减区间是.……………………………………………………… 9分 ‎（Ⅲ）由（Ⅱ）知，在内单调增加，在内单调减少，在上单调增加，且当或时，.……………………………………………… 10分 所以的极大值为，极小值为.……………12分 所以在的三个单调区间直线有的图象各有一个交点，当且仅当.‎ 因此，的取值范围为.……………………………………… 14分 ‎19．解：（Ⅰ）由：知．……………………………………………1分 设，在上，因为，所以，‎ 得，．………………………………………………………………… 3分 在上，且椭圆的半焦距，于是………………………5分 消去并整理得 ， 解得（不合题意，舍去）．‎ 故椭圆的方程为． ………………………………………………… 7分 ‎（Ⅱ）由知四边形是平行四边形，其中心为坐标原点，‎ 因为，所以与的斜率相同，‎ 故的斜率．‎ 设的方程为．……………………………………………………… 8分 由 ………………………………………………………………… 9分 消去并化简得 ．…………………………………… 10分 设，，，.……………………11分 因为，所以．‎ ‎ ．……………… 12分 所以．此时，‎ 故所求直线的方程为，或． …………………… 14分 ‎20.解：（I）由已知，（，）， ………………2分 即（，），且．‎ ‎∴数列是以为首项，公差为1的等差数列．‎ ‎∴．……………………………………………………………………………4分 ‎（II）∵，∴，要使恒成立，‎ ‎∴恒成立，‎ ‎∴恒成立，‎ ‎∴恒成立．……………………………………………………………6分 ‎（ⅰ）当为奇数时，即恒成立，…………………………………………7分 当且仅当时，有最小值为1，‎ ‎∴．………………………………………………………………………………9分 ‎（ⅱ）当为偶数时，即恒成立，………………………………………10分 当且仅当时，有最大值，‎ ‎∴．……………………………………………………………………………12分 即，又为非零整数，则．‎ 综上所述，存在，使得对任意，都有．…………………14分