安徽省芜湖市第一中学高考物理一轮复习 第四章 第7讲 圆周运动动力学两类基本问题2教案（通用） 7页

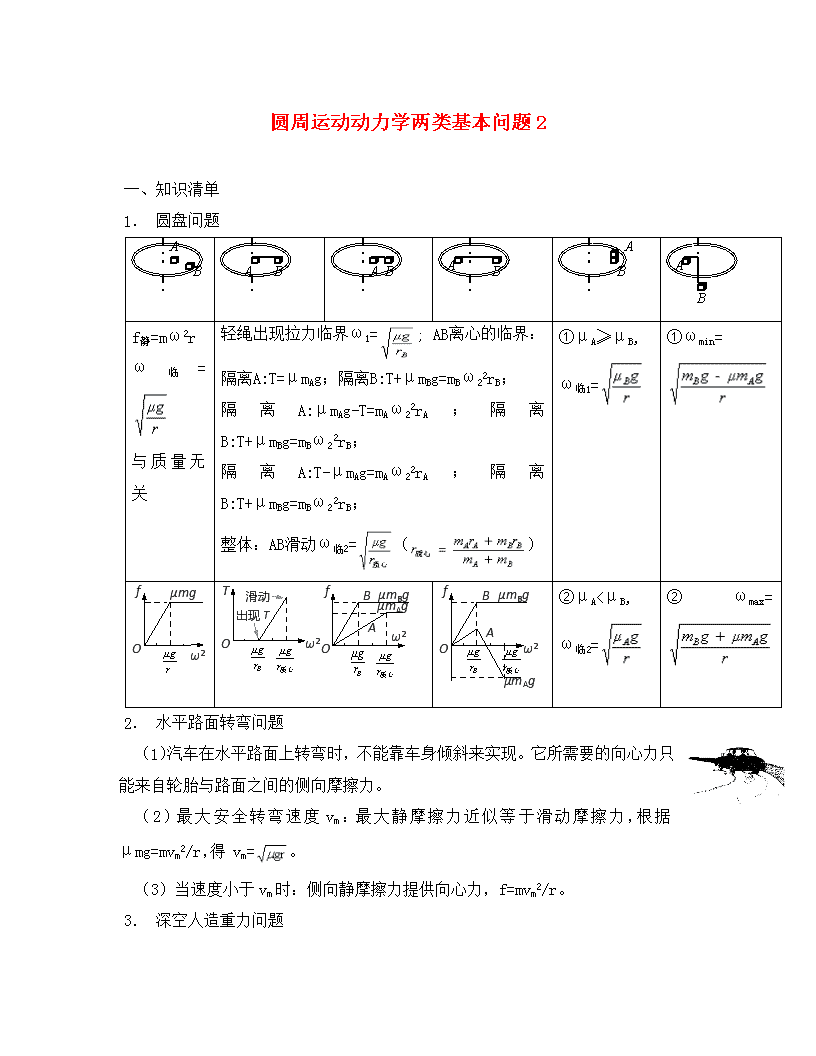
圆周运动动力学两类基本问题2 ‎ 一、知识清单 ‎1． 圆盘问题 A B A B A B A B A B A B f静=mω2r ω临= ‎ 与质量无关 轻绳出现拉力临界ω1=; AB离心的临界：‎ 隔离A:T=μmAg；隔离B:T+μmBg=mBω22rB；‎ 隔离A:μmAg-T=mAω22rA；隔离B:T+μmBg=mBω22rB；‎ 隔离A:T-μmAg=mAω22rA；隔离B:T+μmBg=mBω22rB；‎ 整体：AB滑动ω临2=（）‎ ‎①μA≥μB,‎ ω临1=‎ ‎①ωmin=‎ ω2‎ O f μmg ω2‎ O T 出现T 滑动 ω2‎ O f B μmBg μmAg A ω2‎ O f B μmBg μmAg A ‎②μA<μB,‎ ω临2=‎ ‎②ωmax= ‎ ‎2． 水平路面转弯问题 ‎（1）汽车在水平路面上转弯时，不能靠车身倾斜来实现。它所需要的向心力只能来自轮胎与路面之间的侧向摩擦力。‎ ‎（2）最大安全转弯速度vm：最大静摩擦力近似等于滑动摩擦力，根据μmg=mvm2/r，得 vm=。‎ ‎（3）当速度小于vm时：侧向静摩擦力提供向心力，f=mvm2/r。‎ ‎3． 深空人造重力问题 ‎ ‎ 根据弹力提供向心力可得：mg＝F＝mω2r，即g＝ω2r.‎ 二、例题精讲 ‎4． (多选)如图6所示，两个质量均为m的小木块a和b(可视为质点)放在水平圆盘上，a与转轴OO′的距离为l，b与转轴的距离为‎2l，木块与圆盘的最大静摩擦力为木块所受重力的k倍，重力加速度大小为g.若圆盘从静止开始绕转轴缓慢地加速转动，用ω表示圆盘转动的角速度，下列说法正确的是(　　)‎ A．b一定比a先开始滑动 B．a、b所受的摩擦力始终相等 C．ω＝ 是b开始滑动的临界角速度 D．当ω＝ 时，a所受摩擦力的大小为kmg ‎5． (多选)如图5所示，叠放在水平转台上的物体A、B、C能随转台一起以角速度ω匀速转动，A、B、C的质量分别为‎3m、‎2m、m，A与B、B和C与转台间的动摩擦因数都为μ，A和B、C离转台中心的距离分别为r、1.5r.设本题中的最大静摩擦力等于滑动摩擦力，下列说法正确的是(　　)‎ A．B对A的摩擦力一定为3μmg B．B对A的摩擦力一定为3mω2r C．转台的角速度一定满足：ω≤ D．转台的角速度一定满足：ω≤ ‎6． （多选）如图所示，两个可视为质点的、相同的木块A和B放在转盘上，两者用长为L的细绳连接，木块与转盘的最大静摩擦力均为各自重力的K倍，A放在距离转轴L处，整个装置能绕通过转盘中心的转轴O1O2转动，开始时，绳恰好伸直但无弹力，现让该装置从静止开始转动，使角速度缓慢增大，以下说法正确的是(　　)‎ A．当ω＞时，A、B相对于转盘会滑动 B．当ω＞时，绳子一定有弹力 C．ω在＜ω＜范围内增大时，B所受摩擦力变大 D．ω在0＜ω＜范围内增大时，A所受摩擦力一直变大 ‎7． (多选)如图148所示，在水平转台上放置有轻绳相连的质量相同的滑块1和滑块2，转台绕转轴OO′以角速度ω匀速转动过程中，轻绳始终处于水平状态，两滑块始终相对转台静止，且与转台之间的动摩擦因数相同，滑块1到转轴的距离小于滑块2到转轴的距离。关于滑块1和滑块2受到的摩擦力Ff1和Ff2与ω2的关系图线，可能正确的是(　　)‎ ‎ ‎ ‎8． 如图所示，是某课外研究小组设计的可以用来测量转盘转速的装置。该装置上方是一与转盘固定在一起有横向均匀刻度的标尺，带孔的小球穿在光滑细杆上与一轻弹簧相连，弹簧的另一端固定在转动轴上，小球可沿杆自由滑动并随转盘在水平面内转动。当转盘不转动时，指针指在O处，当转盘转动的角速度为ω1时，指针指在A处，当转盘转动的角速度为ω2时，指针指在B处，设弹簧均没有超过弹性限度。则ω1与ω2的比值为(　　)‎ A. B. C. D. ‎ ‎9． (多选)如图13所示，水平的木板B托着木块A一起在竖直平面内做匀速圆周运动，从水平位置a沿逆时针方向运动到最高点b的过程中，下列说法正确的是(　　)‎ A．木块A处于超重状态 B．木块A处于失重状态 C．B对A的摩擦力越来越小 D．B对A的摩擦力越来越大 ‎10．如图所示为电影《星际穿越》中飞船图片，为了模拟重力环境，可以让飞船旋转起来．对飞行的飞船用Tracker Video Analysis 软件进行分析，得出飞船角速度为0.6rad/s，已知地球表面重力加速度为‎10m/s2，由此推算出飞船的半径约为（ ）‎ A．‎28m B．‎56m C．‎100m D．‎‎256m 三、自我检测 ‎11．(多选)如图10所示，粗糙水平圆盘上，质量相等的A、B两物块叠放在一起，随圆盘一起做匀速圆周运动，则下列说法正确的是(　　)‎ A．B的向心力是A的向心力的2倍 B．盘对B的摩擦力是B对A的摩擦力的2倍 C．A、B都有沿半径向外滑动的趋势 D．若B先滑动，则B对A的动摩擦因数μA小于盘对B的动摩擦因数μB ‎12．(多选)如图14所示，水平放置的两个用相同材料制成的轮P和Q靠摩擦传动，两轮的半径R∶r＝2∶1.当主动轮Q匀速转动时，在Q轮边缘上放置的小木块恰能相对静止在Q轮边缘上，此时Q轮转动的角速度为ω1，木块的向心加速度为a1，若改变转速，把小木块放在P轮边缘也恰能静止，此时Q轮转动的角速度为ω2，木块的向心加速度为a2，则(　　)‎ A.＝ B.＝ C.＝ D.＝ ‎13．如图3所示，一倾斜的匀质圆盘绕垂直于盘面的固定对称轴以恒定角速度ω转动，盘面上离转轴距离‎2.5 m 处有一小物体与圆盘始终保持相对静止。物体与盘面间的动摩擦因数为(设最大静摩擦力等于滑动摩擦力)，盘面与水平面的夹角为30°，g取‎10 m/s2。则ω的最大值是(　　)‎ A. rad/s B. rad/s C.1.0 rad/s D.0.5 rad/s ‎14．(多选)如图所示，AB为圆盘的直径，O为圆盘的圆心，在圆盘边缘A点固定一直立的细杆，一质量为m的物块放在OB的中点，用细线将物块和杆相连，且线刚好拉直但无拉力，转动圆盘的竖直中心轴，使圆盘在水平面内做匀速圆速运动，运动过程中物块与圆盘始终保持相对静止，已知物块与圆盘间的动摩擦因数为μ，圆盘的半径为R，细线能承受的最大拉力F=2μmg，物块与圆盘间的滑动摩擦力等于最大静摩擦力，重力加速度为g，则下列说法正确的是（　　）‎ A．当圆盘转动的角速度为时，绳的拉力为0‎ B A O B．当动的角速度为时，滑块的摩擦力刚好达到最大 C．当圆盘转动的角速度为时，物块受到的摩擦力为μmg D．当绳刚好要断时，圆盘转动的角速度为 ‎15．如图所示，质量M＝‎0.64 kg的物体置于可绕竖直轴匀速转动的平台上，M用细绳通过光滑的定滑轮与质量为m＝‎0.3 kg的物体相连。假定M与轴O的距离r＝‎0.2 m，与平台的最大静摩擦力为2 N。为使m保持静止状态，水平转台做圆周运动的角速度ω应满足(g取‎10 m/s2)（ ）‎ A.ω≤2.80 rad/s B.ω≥6.25 rad/s C.2.80 rad/s≤ω≤6.25 rad/s D.ω≤2.80 rad/s或ω≥6.25 rad/s ‎16．(多选)如图所示，在水平转台的光滑水平横杆上穿有两个质量分别为‎2m和m的小球A和B，A、B间用劲度系数为k的轻质弹簧连接，弹簧的自然长度为L，转台的直径为‎2L，当转台以角速度ω绕坚直轴匀速转动时，如果A、B仍能相对横杆静止而不碰左右两壁，则（　　）‎ A．小球A和B具有相同的角速度 B．小球A和B做圆周运动的半径之比为1：2‎ C．若小球不与壁相碰，则ω＞‎ D．若小球不与壁相碰，则ω＜‎ ‎17．未来的星际航行中，宇航员长期处于零重力状态，为缓解这种状态带来的不适，有人设想在未来的航天器上加装一段圆柱形“旋转舱”，如图2所示．当旋转舱绕其轴线匀速旋转时，宇航员站在旋转舱内圆柱形侧壁上，可以受到与他站在地球表面时相同大小的支持力．为达到上述目的，下列说法正确的是(　　)‎ A．旋转舱的半径越大，转动的角速度就应越大 B．旋转舱的半径越大，转动的角速度就应越小 C．宇航员质量越大，旋转舱的角速度就应越大 D．宇航员质量越大，旋转舱的角速度就应越小 ‎18．图17中给出了一段“S”形单行盘山公路的示意图．弯道1、弯道2可看作两个不同水平面上的圆弧，圆心分别为O1、O2，弯道中心线半径分别为r1＝‎10 m，r2＝‎20 m，弯道2比弯道1高h＝‎12 m，有一直道与两弯道圆弧相切．质量m＝1 ‎‎200 kg 的汽车通过弯道时做匀速圆周运动，路面对轮胎的最大径向静摩擦力是车重的1.25倍，行驶时要求汽车不打滑．(sin 37°＝0.6，sin 53°＝0.8，g＝‎10 m/s2)‎ ‎(1)求汽车沿弯道1中心线行驶时的最大速度v1；‎ ‎(2)汽车以v1进入直道，以P＝30 kW的恒定功率直线行驶了t＝8.0 s进入弯道2，此时速度恰为通过弯道2中心线的最大速度，求直道上除重力以外的阻力对汽车做的功；‎ ‎(3)汽车从弯道1的A点进入，从同一直径上的B点驶离，有经验的司机会利用路面宽度，用最短时间匀速安全通过弯道．设路宽d＝‎10 m，求此最短时间(A、B两点都在轨道的中心线上，计算时视汽车为质点)．‎