高考真题数学理浙江卷 5页

‎2012年普通高等学校招生全国统一考试 数学（理科）‎ 一、 选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的。‎ 1. 设集合A={x|1＜x＜4}，集合B ={x|-2x-3≤0}, 则A∩（CRB）=‎ A .(1,4) B .(3,4) C.(1,3) D .(1,2)∪（3,4）‎ ‎2. 已知i是虚数单位，则=‎ A .1-2i 　　　　　B.2-i 　　C.2+i D .1+2i ‎ ‎3. 设a∈R ，则“a＝‎1”‎是“直线l1：ax+2y=0与直线l2 ：x+(a+1)y+4=0平行 的 A 充分不必要条件 　　　B 必要不充分条件 ‎ C 充分必要条件 　　　　　D 既不充分也不必要条件 ‎4.把函数y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），然后向左平移1个单位长度，再向下平移 1个单位长度，得到的图像是 ‎5.设a，b是两个非零向量。‎ A.若|a+b|=|a|-|b|，则a⊥b B.若a⊥b，则|a+b|=|a|-|b|‎ C.若|a+b|=|a|-|b|，则存在实数λ，使得b=λa D.若存在实数λ，使得b=λa，则|a+b|=|a|-|b|‎ ‎6.若从1,2,3，…，9这9个整数中同时取4个不同的数，其和为偶数，则不同的取法共有 A.60种 　　　B.63种 　　　C.65种 　　D.66种 ‎7.设S。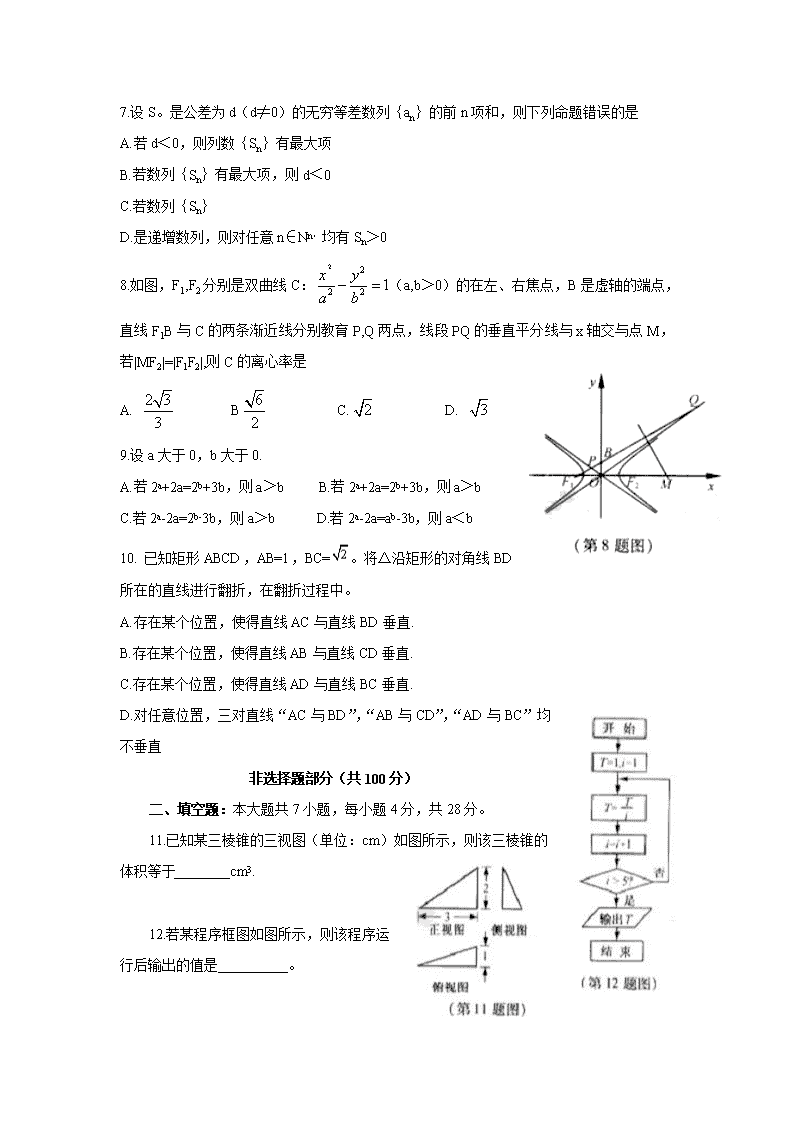是公差为d（d≠0）的无穷等差数列﹛an﹜的前n项和，则下列命题错误的是 A.若d＜0，则列数﹛Sn﹜有最大项 B.若数列﹛Sn﹜有最大项，则d＜0‎ C.若数列﹛Sn﹜‎ D.是递增数列，则对任意n∈Nn，均有Sn＞0‎ ‎8.如图，F1,F2分别是双曲线C：（a,b＞0）的在左、右焦点，B是虚轴的端点，直线F1B与C的两条渐近线分别教育P,Q两点，线段PQ的垂直平分线与x轴交与点M，若|MF2|=|F‎1F2|,则C的离心率是 A. B C. D. ‎ ‎9.设a大于0，b大于0.‎ A.若‎2a+‎2a=2b+3b，则a＞b B.若‎2a+‎2a=2b+3b，则a＞b C.若‎2a-2a=2b-3b，则a＞b D.若‎2a-2a=ab-3b，则a＜b ‎10. 已知矩形ABCD，AB=1，BC=。将△沿矩形的对角线BD所在的直线进行翻折，在翻折过程中。‎ A.存在某个位置，使得直线AC与直线BD垂直.‎ B.存在某个位置，使得直线AB与直线CD垂直.‎ C.存在某个位置，使得直线AD与直线BC垂直.‎ D.对任意位置，三对直线“AC与BD”，“AB与CD”，“AD与BC”均不垂直 非选择题部分（共100分）‎ 二、填空题：本大题共7小题，每小题4分，共28分。‎ ‎11.已知某三棱锥的三视图（单位：cm）如图所示，则该三棱锥的体积等于________cm3.‎ ‎12.若某程序框图如图所示，则该程序运行后输出的值是__________。‎ ‎13.设公比为q（q＞0）的等比数列{an}的前n项和为Sn。若S2=‎3a2+2，S4=‎3a4+2，则q=______________。‎ ‎14.若将函数f（x）=x5表示为f（x）=a0＋a1（1＋x）＋a2（1＋x）2＋……＋a5（1＋x）5，其中a0，a1，a2，…a5为实数，则a3=______________。‎ ‎15.在△ABC中，M是BC的中点，AM=3，BC=10，则=________.‎ ‎ 16．定义：曲线C上的点到直线l的距离的最小值称为曲线C到直线l的距离，已知曲线C1：y=x2+a到直线l:y=x的距离等于曲线C2：x2+(y+4)2=2到直线l:y=x的距离，则实数a=_______。‎ ‎17．设a∈R，若x>0时均有[(a-1)x-1](x2-ax-1)≥0，则a=__________。‎ 三、解答题：本大题共5小题，共72分。解答应写出文字说明、证明过程或演算步骤。‎ ‎18.（本题满分14分）在△ABC中，内角A，B，C的对边分别为a，b，c。已知cosA=，sinB=C。‎ ‎（1）求tanC的值；‎ ‎（2）若a=，求△ABC的面积。‎ ‎19.（本题满分14分）已知箱中装有4个白球和5个黑球，且规定：取出一个白球得2分，取出一个黑球得1分。现从该箱中任取（无放回，且每球取到的机会均等）3个球，记随机变量X为取出此3球所得分数之和。‎ ‎（1）求X的分布列；‎ ‎（2）求X的数学期望E（X）。‎ ‎20.（本题满分14分）如图，在四棱锥P-ABCD中，底面是边长为的菱形，∠BAD=120°，且PA⊥平面ABCD，PA=,M，N分别为PB,PD的中点。‎ ‎（1）证明：MN∥平民啊ABCD；‎ ‎（2）过点A作AQ⊥‎ PC，垂足为点Q，求二面角A-MN-Q的平面角的余弦值。‎ ‎21.（本题满分15分）如图，椭圆的离心率为，其左焦点到点Ｐ（２,１）的距离为，不过原点Ｏ的直线ｌ与Ｃ相交于Ａ，Ｂ两点，且线段ＡＢ被直线ＯＰ平分。‎ ‎（Ⅰ）求椭圆C的方程；‎ ‎（Ⅱ）求△APB面积取最大值时直线l的方程。‎ ‎22.（本题满分14分）已知a>0,b∈R，函数f(x)=4ax2-2bx-a+b。‎ ‎（Ⅰ）证明：当0x1时。‎ ‎（1）函数f(x)的最大值为|‎ ‎（2）f(x)+ +a 0;‎ ‎（Ⅱ）若-1 f(x) 1对x∈恒成立，求a+b的取值范围。‎