2020-2021学年高考数学（理）考点：双曲线 43页

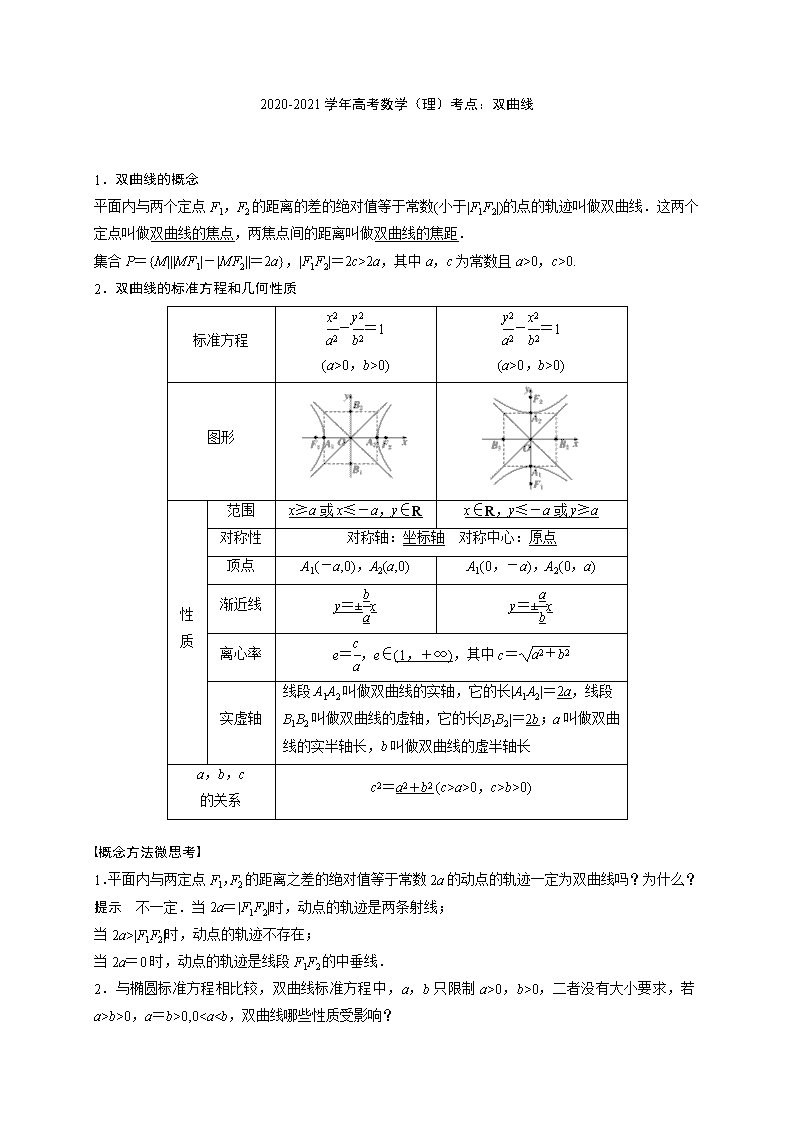
‎2020-2021学年高考数学（理）考点：双曲线 ‎1．双曲线的概念 平面内与两个定点F1，F2的距离的差的绝对值等于常数(小于|F1F2|)的点的轨迹叫做双曲线．这两个定点叫做双曲线的焦点，两焦点间的距离叫做双曲线的焦距．‎ 集合P＝{M|||MF1|－|MF2||＝2a}，|F1F2|＝2c>2a，其中a，c为常数且a>0，c>0.‎ ‎2．双曲线的标准方程和几何性质 标准方程 －＝1‎ ‎(a>0，b>0)‎ －＝1‎ ‎(a>0，b>0)‎ 图形 性 质 范围 x≥a或x≤－a，y∈R x∈R，y≤－a或y≥a 对称性 对称轴：坐标轴　对称中心：原点 顶点 A1(－a,0)，A2(a,0)‎ A1(0，－a)，A2(0，a)‎ 渐近线 y＝±x y＝±x 离心率 e＝，e∈(1，＋∞)，其中c＝ 实虚轴 线段A1A2叫做双曲线的实轴，它的长|A1A2|＝2a，线段B1B2叫做双曲线的虚轴，它的长|B1B2|＝2b；a叫做双曲线的实半轴长，b叫做双曲线的虚半轴长 a，b，c 的关系 c2＝a2＋b2 (c>a>0，c>b>0)‎ 概念方法微思考 ‎1．平面内与两定点F1，F2的距离之差的绝对值等于常数2a的动点的轨迹一定为双曲线吗？为什么？‎ 提示　不一定．当2a＝|F1F2|时，动点的轨迹是两条射线；‎ 当2a>|F1F2|时，动点的轨迹不存在；‎ 当2a＝0时，动点的轨迹是线段F1F2的中垂线．‎ ‎2．与椭圆标准方程相比较，双曲线标准方程中，a，b只限制a>0，b>0，二者没有大小要求，若a>b>0，a＝b>0,0b>0时，10时，e＝(亦称等轴双曲线)；当0.‎ ‎1．（2020•天津）设双曲线的方程为，过抛物线的焦点和点的直线为．若的一条渐近线与平行，另一条渐近线与垂直，则双曲线的方程为　　‎ A． B． C． D．‎ ‎【答案】D ‎【解析】抛物线的焦点坐标为，‎ 则直线的方程为，‎ 双曲线的方程为的渐近线方程为，‎ 的一条渐近线与平行，另一条渐近线与垂直，‎ ‎，，‎ ‎，，‎ 双曲线的方程为，‎ 故选．‎ ‎2．（2020•新课标Ⅰ）设，是双曲线的两个焦点，为坐标原点，点在上且，则△的面积为　　‎ A． B．3 C． D．2‎ ‎【答案】B ‎【解析】由题意可得，，，‎ ‎，‎ ‎，‎ ‎，‎ ‎△为直角三角形，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ ‎△的面积为，‎ 故选．‎ ‎3．（2020•新课标Ⅲ）设双曲线的左、右焦点分别为，，离心率为．是上一点，且．若△的面积为4，则　　‎ A．1 B．2 C．4 D．8‎ ‎【答案】A ‎【解析】由题意，设，，可得，，，，‎ 可得，可得，‎ 解得．‎ 故选．‎ ‎4．（2019•全国）已知双曲线，过的左焦点且垂直于轴的直线交于，两点，若以为直径的圆经过的右焦点，则的离心率为　　‎ A． B．2 C． D．‎ ‎【答案】A ‎【解析】设双曲线的左焦点为，右焦点为，‎ 以为直径的圆恰好过双曲线的右焦点，，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ 故选．‎ ‎5．（2019•新课标Ⅲ）已知是双曲线的一个焦点，点在上，为坐标原点．若，则的面积为　　‎ A． B． C． D．‎ ‎【答案】B ‎【解析】如图，不妨设为双曲线的右焦点，为第一象限点．‎ 由双曲线方程可得，，，则，‎ 则以为圆心，以3为半径的圆的方程为．‎ 联立，解得，．‎ ‎．‎ 故选．‎ ‎6．（2019•新课标Ⅲ）双曲线的右焦点为，点在的一条渐近线上，为坐标原点．若，则的面积为　　‎ A． B． C． D．‎ ‎【答案】A ‎【解析】双曲线的右焦点为，，渐近线方程为：，不妨在第一象限，‎ 可得，，，‎ 所以的面积为：．‎ 故选．‎ ‎7．（2019•浙江）渐近线方程为的双曲线的离心率是　　‎ A． B．1 C． D．2‎ ‎【答案】C ‎【解析】根据渐近线方程为的双曲线，可得，所以 则该双曲线的离心率为，‎ 故选．‎ ‎8．（2019•北京）已知双曲线的离心率是，则　　‎ A． B．4 C．2 D．‎ ‎【答案】D ‎【解析】由双曲线，得，‎ 又，得，即，‎ 解得，．‎ 故选．‎ ‎9．（2019•新课标Ⅱ）设为双曲线的右焦点，为坐标原点，以为直径的圆与圆交于，两点．若，则的离心率为　　‎ A． B． C．2 D．‎ ‎【答案】A ‎【解析】如图，‎ 由，可知过点，，‎ 由图可得，得．‎ 故选．‎ ‎10．（2019•新课标Ⅰ）双曲线的一条渐近线的倾斜角为，则的离心率为　　‎ A． B． C． D．‎ ‎【答案】D ‎【解析】双曲线的渐近线方程为，‎ 由双曲线的一条渐近线的倾斜角为，得，‎ 则，‎ ‎，‎ 得，‎ ‎．‎ 故选．‎ ‎11．（2018•天津）已知双曲线的离心率为2，过右焦点且垂直于轴的直线与双曲线交于，两点．设，到双曲线的同一条渐近线的距离分别为和，且，则双曲线的方程为　　‎ A． B． C． D．‎ ‎【答案】A ‎【解析】由题意可得图象如图，是双曲线的一条渐近线 ‎，即，，‎ ‎，，，是梯形，‎ 是的中点，，‎ ‎，‎ 所以，双曲线的离心率为2，可得，‎ 可得：，解得．‎ 则双曲线的方程为：．‎ 故选．‎ ‎12．（2018•天津）已知双曲线的离心率为2，过右焦点且垂直于轴的直线与双曲线交于，两点．设，到双曲线的同一条渐近线的距离分别为和，且，则双曲线的方程为　　‎ A． B． C． D．‎ ‎【答案】C ‎【解析】由题意可得图象如图，是双曲线的一条渐近线 ‎，即，，‎ ‎，，，是梯形，‎ 是的中点，，‎ ‎，‎ 所以，双曲线的离心率为2，可得，‎ 可得：，解得．‎ 则双曲线的方程为：．‎ 故选．‎ ‎13．（2018•浙江）双曲线的焦点坐标是　　‎ A．，，， B．， ‎ C．， D．，‎ ‎【答案】B ‎【解析】双曲线方程可得双曲线的焦点在轴上，且，，‎ 由此可得，‎ 该双曲线的焦点坐标为 故选．‎ ‎14．（2018•新课标Ⅲ）已知双曲线的离心率为，则点到的渐近线的距离为　　‎ A． B．2 C． D．‎ ‎【答案】D ‎【解析】双曲线的离心率为，‎ 可得，即：，解得，‎ 双曲线的渐近线方程为：，‎ 点到的渐近线的距离为：．‎ 故选．‎ ‎15．（2018•新课标Ⅲ）设，是双曲线．的左，右焦点，是坐标原点．过作的一条渐近线的垂线，垂足为，若，则的离心率为　　‎ A． B．2 C． D．‎ ‎【答案】C ‎【解析】双曲线．的一条渐近线方程为，‎ 点到渐近线的距离，即，‎ ‎，，‎ ‎，‎ ‎，‎ 在三角形中，由余弦定理可得，‎ ‎，‎ 即，‎ 即，‎ ‎，‎ 故选．‎ ‎16．（2018•新课标Ⅱ）双曲线的离心率为，则其渐近线方程为　　‎ A． B． C． D．‎ ‎【答案】A ‎【解析】双曲线的离心率为，‎ 则，‎ 即双曲线的渐近线方程为，‎ 故选．‎ ‎17．（2018•新课标Ⅰ）已知双曲线，为坐标原点，为的右焦点，过的直线与的两条渐近线的交点分别为，．若为直角三角形，则　　‎ A． B．3 C． D．4‎ ‎【答案】B ‎【解析】双曲线的渐近线方程为：，渐近线的夹角为：，不妨设过的直线为：，‎ 则：解得，，‎ 解得：，‎ 则．‎ 故选．‎ ‎18．（2017•全国）已知双曲线的右焦点为，直线与的右支有两个交点，则　　‎ A． B． C． D．‎ ‎【答案】B ‎【解析】双曲线的渐近线方程为 ‎，‎ 由直线与的右支有两个交点，‎ 且直线经过右焦点，‎ 可得，‎ 故选．‎ ‎19．（2017•天津）已知双曲线的右焦点为，点在双曲线的渐近线上，是边长为2的等边三角形为原点），则双曲线的方程为　　‎ A． B． C． D．‎ ‎【答案】D ‎【解析】双曲线的右焦点为，点在双曲线的渐近线上，是边长为2的等边三角形为原点），‎ 可得，，即，，‎ 解得，，双曲线的焦点坐标在轴，所得双曲线方程为：．‎ 故选．‎ ‎20．（2017•新课标Ⅰ）已知是双曲线的右焦点，是上一点，且与轴垂直，点的坐标是，则的面积为　　‎ A． B． C． D．‎ ‎【答案】D ‎【解析】由双曲线的右焦点，‎ 与轴垂直，设，，则，‎ 则，‎ ‎，则，，‎ 的面积，‎ 同理当时，则的面积，‎ 故选．‎ ‎21．（2017•新课标Ⅲ）已知双曲线的一条渐近线方程为，且与椭圆有公共焦点，则的方程为　　‎ A． B． C． D．‎ ‎【答案】B ‎【解析】椭圆的焦点坐标，‎ 则双曲线的焦点坐标为，可得，‎ 双曲线的一条渐近线方程为，‎ 可得，即，可得，解得，，‎ 所求的双曲线方程为：．‎ 故选．‎ ‎22．（2017•新课标Ⅱ）若，则双曲线的离心率的取值范围是　　‎ A．， B．， C． D．‎ ‎【答案】C ‎【解析】，则双曲线的离心率为：．‎ 故选．‎ ‎23．（2020•北京）已知双曲线，则的右焦点的坐标为　　；的焦点到其渐近线的距离是__________．‎ ‎【答案】，‎ ‎【解析】双曲线，则，则，则的右焦点的坐标为，‎ 其渐近线方程为，即，‎ 则点到渐近线的距离，‎ 故答案为：，．‎ ‎24．（2020•新课标Ⅲ）设双曲线的一条渐近线为，则的离心率为__________．‎ ‎【答案】‎ ‎【解析】由双曲线的方程可得渐近线的方程为：，‎ 由题意可得，所以离心率，‎ 故答案为：．‎ ‎25．（2020•江苏）在平面直角坐标系中，若双曲线的一条渐近线方程为，则该双曲线的离心率是__________．‎ ‎【答案】‎ ‎【解析】双曲线的一条渐近线方程为，可得，所以，‎ 所以双曲线的离心率为：，‎ 故答案为：．‎ ‎26．（2020•新课标Ⅰ）已知为双曲线的右焦点，为的右顶点，为上的点，且垂直于轴．若的斜率为3，则的离心率为__________．‎ ‎【答案】2‎ ‎【解析】为双曲线的右焦点，为的右顶点，‎ 为上的点，且垂直于轴．所以，‎ 若的斜率为3，可得：，‎ ‎，代入上式化简可得，，‎ 可得，，‎ 解得．‎ 故答案为：2．‎ ‎27．（2019•上海）已知数列满足，，均在双曲线上，则__________．‎ ‎【答案】‎ ‎【解析】法一：由，可得，‎ ‎，，‎ ‎，，‎ 求解极限可得．‎ 方法二：当时，与渐近线平行，在轴的投影为1，渐近线倾斜角为，则，‎ 故 故答案为：．‎ ‎28．（2019•江苏）在平面直角坐标系中，若双曲线经过点，则该双曲线的渐近线方程是__________．‎ ‎【答案】‎ ‎【解析】双曲线经过点，‎ ‎，解得，即．‎ 又，该双曲线的渐近线方程是．‎ 故答案为：．‎ ‎29．（2019•新课标Ⅰ）已知双曲线的左、右焦点分别为，，过的直线与的两条渐近线分别交于，两点．若，，则的离心率为__________．‎ ‎【答案】2‎ ‎【解析】如图，‎ ‎，为的中点，且为的中点，‎ 为△的中位线，‎ 又，，则．‎ 设，，，，‎ 点在渐近线上，‎ ‎，得．‎ 又为的中点，，‎ 在渐近线上，‎ ‎，得，则双曲线的离心率．‎ 故答案为：2．‎ ‎30．（2018•江苏）在平面直角坐标系中，若双曲线的右焦点到一条渐近线的距离为，则其离心率的值为__________．‎ ‎【答案】2‎ ‎【解析】双曲线的右焦点到一条渐近线的距离为，‎ 可得：，‎ 可得，即，‎ 所以双曲线的离心率为：．‎ 故答案为：2．‎ ‎31．（2018•北京）若双曲线的离心率为，则__________．‎ ‎【答案】4‎ ‎【解析】双曲线的离心率为，‎ 可得：，解得．‎ 故答案为：4．‎ ‎32．（2018•上海）双曲线的渐近线方程为__________．‎ ‎【答案】‎ ‎【解析】双曲线的，，焦点在轴上 ‎ 而双曲线的渐近线方程为 双曲线的渐近线方程为 故答案为：．‎ ‎33．（2017•上海）设双曲线的焦点为、，为该双曲线上的一点，若，则__________．‎ ‎【答案】11‎ ‎【解析】根据题意，双曲线的方程为：，‎ 其中，‎ 则有，‎ 又由，‎ 解可得或（舍 故，‎ 故答案为：11．‎ ‎34．（2017•北京）若双曲线的离心率为，则实数__________．‎ ‎【答案】2‎ ‎【解析】双曲线的离心率为，‎ 可得：，‎ 解得．‎ 故答案为：2．‎ ‎35．（2017•新课标Ⅰ）已知双曲线的右顶点为，以为圆心，为半径作圆，圆与双曲线的一条渐近线交于、两点．若，则的离心率为__________．‎ ‎【答案】‎ ‎【解析】双曲线的右顶点为，‎ 以为圆心，为半径做圆，圆与双曲线的一条渐近线交于、两点．‎ 若，可得到渐近线的距离为：，‎ 可得：，即，可得离心率为：．‎ 故答案为：．‎ ‎36．（2017•江苏）在平面直角坐标系中，双曲线的右准线与它的两条渐近线分别交于点，，其焦点是，，则四边形的面积是__________．‎ ‎【答案】‎ ‎【解析】双曲线的右准线：，双曲线渐近线方程为：，‎ 所以，，，，．．‎ 则四边形的面积是：．‎ 故答案为：．‎ ‎37．（2018•全国）双曲线，、为其左右焦点，是以为圆心且过原点的圆．‎ ‎（1）求的轨迹方程；‎ ‎（2）动点在上运动，满足，求的轨迹方程．‎ ‎【解析】（1）由已知得，，故，所以、，‎ 因为是以为圆心且过原点的圆，故圆心为，半径为4，‎ 所以的轨迹方程为；‎ ‎（2）设动点，，，‎ 则，，‎ 由，得，，，‎ 即，解得，‎ 因为点在上，所以，‎ 代入得，‎ 化简得．‎ ‎38．（2017•上海）已知双曲线，直线，与交于、两点，为关于轴的对称点，直线与轴交于点；‎ ‎（1）若点是的一个焦点，求的渐近线方程；‎ ‎（2）若，点的坐标为，且，求的值；‎ ‎（3）若，求关于的表达式．‎ ‎【解析】（1）双曲线，点是的一个焦点，‎ ‎，，，‎ 的标准方程为：，‎ 的渐近线方程为．‎ ‎（2），双曲线为：，，，‎ ‎，设，，‎ 则有定比分点坐标公式，得：‎ ‎，解得，，，‎ ‎．‎ ‎（3）设，，，，，‎ 则，，，‎ 由，得，‎ ‎，，‎ 由，得，‎ ‎，，‎ ‎，即，即，‎ ‎，‎ 化简，得，‎ 或，‎ 当，由，得，‎ 由，得，‎ 即，，代入，化简，得：‎ ‎，解得或，‎ 当时，满足，‎ 当时，由，得（舍去），‎ 综上，得．‎ 强化训练 ‎1．（2020•江西模拟）圆与双曲线的两条渐近线相切于、两点，若，则的离心率为　　‎ A． B． C．2 D．3‎ ‎【答案】A ‎【解析】圆的圆心为，‎ 双曲线的两条渐近线方程为，‎ 由圆和两条渐近线都关于轴对称，可设，，，，‎ 由题意可得，则，‎ 由为切点，直线与渐近线垂直，‎ 可得，则，‎ 可得双曲线的离心率为，‎ 故选．‎ ‎2．（2020•红岗区校级模拟）已知双曲线的左、右焦点分别为、，过点且垂直于轴的直线与该双曲线的左支交于、两点，若的周长为24，则当取得最大值时，该双曲线的焦点到渐近线的距离为　　‎ A．1 B． C．2 D．‎ ‎【答案】D ‎【解析】可设，由代入双曲线的方程可得，‎ 则，，‎ 由题意可得，‎ 结合，上式化简可得，可得，‎ 则，‎ 设，，导数为，‎ 当时，，递减；当时，，递增．‎ 可得在处取得最大值．‎ 即有，，即，‎ 而焦点到渐近线的距离为，‎ 故选．‎ ‎3．（2020•湖北模拟）已知双曲线的右顶点为，为坐标原点，以为圆心的圆与双曲线的某一条渐近线交于两点，，若且，则双曲线的离心率为　　‎ A． B． C． D．‎ ‎【答案】A ‎【解析】，，‎ 又， 是等腰直角三角形，‎ ‎，渐近线方程不妨为，即 则 到该渐近线的距离为 ‎，‎ 又，，‎ 又，‎ 由余弦定理，‎ 得，‎ 整理得，，‎ 故选．‎ ‎4．（2020•运城模拟）当变化时，对于双曲线，值不变的是　　‎ A．实轴长 B．虚轴长 C．焦距 D．离心率 ‎【答案】D ‎【解析】由题意可得，，，显然双曲线实轴长，虚轴长，焦距都是变量；‎ 而是常数．‎ 故选．‎ ‎5．（2020•镜湖区校级模拟）双曲线左、右焦点分别为，，一条渐近线与直线垂直，点在上，且，则　　‎ A．6或30 B．6 C．30 D．6或20‎ ‎【答案】C ‎【解析】双曲线左、右焦点分别为，，一条渐近线与直线垂直，‎ 可得，解得，‎ 点在上，，所以在双曲线的右支上，‎ 则．‎ 故选．‎ ‎6．（2020•香坊区校级一模）已知双曲线的右焦点为，过作双曲线一条渐近线的垂线，垂足为点，且与另一条渐近线交于点，若，则双曲线方程为　　‎ A． B． C． D．‎ ‎【答案】B ‎【解析】由题意可得，即，‎ 双曲线的渐近线方程为，‎ 设在渐近线上，可得，‎ 若，则为的中点如图，‎ 且，可得为等腰三角形，‎ 则，‎ 在直角三角形中，可得，‎ 即，，‎ 则双曲线的方程为．‎ 故选．‎ ‎7．（2020•二模拟）双曲线的左、右焦点分别为，，过其中一个焦点作轴的垂线，与交于，两点，若，则双曲线的离心率为　　‎ A． B． C． D．‎ ‎【答案】B ‎【解析】由题意可知，双曲线的通径为：，双曲线的左、右焦点分别为，，过其中一个焦点作轴的垂线，与交于，两点，若，‎ 可得，即：，即，．‎ 解得．‎ 故选．‎ ‎8．（2020•南岗区校级模拟）已知双曲线的右焦点为，和为双曲线上关于原点对称的两点，且在第一象限．连结并延长交于，连结，，若△是以为直角的等腰直角三角形，则双曲线的离心率为　　‎ A． B． C． D．‎ ‎【答案】C ‎【解析】设双曲线的半焦距为，，‎ 由，，可得四边形为平行四边形，‎ 则，且，‎ 连接，由双曲线的定义可得，‎ 又，‎ 在直角三角形中，可得，①‎ 在直角三角形中，可得，‎ 化为，代入①可得，‎ 即有，即．‎ 故选．‎ ‎9．（2020•安徽模拟）已知双曲线的离心率为2．则其渐近线的方程为　　‎ A． B． C． D．‎ ‎【答案】A ‎【解析】双曲线的离心率为2．‎ 可得：，即，‎ 可得，‎ 则双曲线的渐近线方程为：．‎ 故选．‎ ‎10．（2020•汉阳区校级模拟）已知为双曲线的右支上一点，、为其左、右焦点，且焦距的长度为6，为的角平分线，是与轴的交点，是坐标原点，满足，，则双曲线的离心率为　　‎ A． B． C． D．‎ ‎【答案】A ‎【解析】如图，焦距的长度为6，满足，，‎ 故，；‎ 为的角平分线，‎ ‎；‎ 设，则；‎ ‎△中，；①‎ ‎△中，；②‎ 联立①②可得：；‎ ‎；‎ ‎．‎ 故选．‎ ‎11．（2020•东湖区校级三模）已知、为双曲线的左、右焦点，点为右支上一点．若恰好被轴平分，且，则的渐近线方程为　　‎ A． B． C． D．‎ ‎【答案】B ‎【解析】、为双曲线的左、右焦点，点为右支上一点，‎ 若恰好被轴平分，‎ 则垂直轴，因为，‎ 所以，可得，，可得，‎ 可得，则．‎ 则的渐近线方程为．‎ 故选．‎ ‎12．（2020•辽宁模拟）已知，分别为双曲线的两个焦点，双曲线上的点到原点的距离为，且，则该双曲线的渐近线方程为　　‎ A． B． C． D．‎ ‎【答案】A ‎【解析】，分别为双曲线的两个焦点，‎ 不妨设双曲线的焦点坐标为、，‎ ‎，所以，，‎ ‎，，双曲线上的点到原点的距离为，所以，‎ ‎，，，，，设，，，把点的坐标代入双曲线方程可得：，‎ 该双曲线的渐近线方程．‎ 故选．‎ ‎13．（2020•碑林区校级模拟）双曲线的左、右焦点为，，以为圆心，为半径作圆，过作直线与圆切于点，若在双曲线的渐近线上，则双曲线的离心率为　　‎ A． B． C．2 D．‎ ‎【答案】C ‎【解析】 为圆的切线，故，‎ 又，，‎ ‎，，‎ ‎．‎ 故选．‎ ‎14．（2020•思明区校级一模）已知、为双曲线的左、右焦点，点在双曲线的右支上，线段与双曲线的左支交于点，，‎ ‎，则双曲线的离心率为　　‎ A． B． C． D．‎ ‎【答案】C ‎【解析】如图所示：，‎ 不妨设，‎ ‎，‎ ‎，，‎ ‎，，‎ 在中，由余弦定理可得，‎ 即，‎ 解得，‎ ‎，，‎ 在△中，由余弦定理可得，‎ 即，‎ 整理可得，‎ 即．‎ 故选．‎ ‎15．（2020•黄州区校级三模）已知双曲线，过左焦点作斜率为的直线与双曲线的一条渐近线相交于点，且在第一象限，若，则双曲线的离心率为　　‎ A． B． C．2 D．‎ ‎【答案】A ‎【解析】由题意可得直线的方程为：，与渐近线联立，‎ 可得，，‎ 因为，即，‎ 整理可得，，即，‎ 因为，‎ 解得．‎ 故选．‎ ‎16．（2020•吉林模拟）已知是双曲线的左焦点，为双曲线右支上一点，圆与轴的正半轴交点为，的最小值4，则双曲线的实轴长为　　‎ A． B．2 C． D．‎ ‎【答案】B ‎【解析】由题意，，设为双曲线的右焦点，则，，，，．‎ ‎，‎ 三点，，共线时取等号．‎ 所以，解得，故实轴长为2．‎ 故选．‎ ‎17．（2020•松原模拟）已知点是双曲线上一点，，分别为双曲线的左、右焦点，若△的外接圆半径为4，且为锐角，则　　‎ A．15 B．16 C．18 D．20‎ ‎【答案】B ‎【解析】点是双曲线上一点，，，，，‎ ‎△的外接圆半径为4，可得圆的圆心，圆的方程为：，不妨设在第一象限，‎ 圆的方程与双曲线联立可得，‎ ‎．‎ 故选．‎ ‎18．（2020•红岗区校级模拟）双曲线的渐近线方程是，则双曲线的焦距为　　‎ A．3 B．6 C． D．‎ ‎【答案】B ‎【解析】双曲线的渐近线方程是，‎ 可得，所以，‎ 所以双曲线的焦距为6．‎ 故选．‎ ‎19．（2020•龙潭区校级模拟）设双曲线的渐近线方程为，则双曲线的离心率为　　‎ A． B． C． D．‎ ‎【答案】D ‎【解析】双曲线的渐近线方程为，‎ 可得，所以，即，‎ 所以双曲线的离心率为：．‎ 故选．‎ ‎20．（2020•运城模拟）过双曲线的左焦点且斜率为的直线与双曲线的两条渐近线分别交于，两点，与轴交于点，若，则双曲线的离心率等于　　‎ A． B． C． D．‎ ‎【答案】D ‎【解析】依题意可知点在第二象限，点在第一象限，直线方程为，‎ 由得，由得，，‎ 由，可得，即整理得，‎ 又因为，所以，得，‎ 所以．‎ 故选．‎ ‎21．（2020•大同模拟）已知双曲线的右焦点，半焦距，点到直线的距离为，过点作双曲线的两条互相垂直的弦，，设，的中点分别为，．‎ ‎（1）求双曲线的标准方程；‎ ‎（2）证明：直线必过定点，并求出此定点的坐标．‎ ‎【解析】（1）由题意可得，，，解得：，，‎ 所以双曲线的方程为：；‎ ‎（2）证明：设设过的弦所在的直线方程为：，，，，，‎ 则有中点，，‎ 联立直线与双曲线的方程：整理可得：，‎ 因为弦与双曲线有两个交点，所以，‎ ‎，所以，‎ 所以，；‎ 当时，点即是，此时直线为轴；‎ 当时，将的坐标中的换成，‎ 同理可得的坐标，，‎ ‎①当直线不垂直于轴时，‎ 直线的斜率，‎ 将代入方程可得直线，‎ 化简可得，‎ 所以直线恒过定点；‎ ‎②当直线垂直于轴时，可得，直线也过定点；‎ 综上所述直线恒过定点．‎ ‎22．（2019•陕西三模）设离心率为3，实轴长为1的双曲线的左焦点为，顶点在原点的抛物线的准线经过点，且抛物线的焦点在轴上．‎ 求抛物线的方程；‎ ‎（Ⅱ）若直线与抛物线交于不同的两点，，且满足，求的最小值．‎ ‎【解析】离心率为3，实轴长为1，即，，‎ 可得，，，‎ 可设抛物线的方程为，，‎ 可得，即，‎ 可得抛物线的方程为；‎ ‎（Ⅱ）设直线的方程为，设点，、，，‎ 则，，‎ 将直线的方程与抛物线的方程联立，得，‎ 由韦达定理得，，‎ ‎，，即，‎ ‎ 由△恒成立，‎ 则 ‎，‎ 当且仅当时，取得最小值12．‎ ‎23．（2019•天河区校级三模）已知双曲线的焦点在轴上，焦距为4，且的渐近线方程为．‎ ‎（1）求双曲线的方程；‎ ‎（2）若直线与椭圆及双曲线都有两个不同的交点，且与的两个交点和满足（其中为原点），求的取值范围．‎ ‎【解析】（1）根据题意，的渐近线方程为，则设双曲线的方程为，则，，‎ 又双曲线的焦距为4，则，即，‎ 于是由，‎ 故的方程为；‎ ‎（2）根据题意，将代入得，‎ 由直线与椭圆有两个不同的交点得，即，①‎ 将代入得，‎ 由直线与双曲线有两个不同的交点，，‎ 则有，即且，②‎ 设，，，，则，，‎ 则得，‎ 而，‎ 于是，解此不等式得，或，③‎ 由①，②，③得，或，‎ 故的取值范围为．‎ ‎24．（2019•龙岩模拟）双曲线的左右顶点分别为，，动直线垂直的实轴，且交于不同的两点，，直线与直线的交点为．‎ ‎（1）求点的轨迹的方程；‎ ‎（2）过点作的两条互相垂直的弦，，证明：过两弦，中点的直线恒过定点．‎ ‎【解析】（1）因为，，‎ 设，，，则，，且，①，‎ 因为动直线交双曲线于不同的两点，，所以且，‎ 因为直线的方程为，②，‎ 直线的方程为，③，‎ 由②③得，‎ 把①代入上式得，化简得，‎ 所以点的轨迹的方程为．‎ ‎（2）依题意得直线与直线斜率均存在且不为0，‎ 设直线的方程为，则直线的方程为，‎ 联立，得，‎ 则△，‎ 设，，，，则，，‎ 所以的中点，，‎ 同理的中点，，‎ 所以直线的斜率为，‎ 所以直线的方程为，‎ 整理得，‎ 所以直线恒过定点，，即过两弦，中点的直线恒过定点，．‎ ‎25．（2019•丹东一模）已知离心率为2的双曲线的一个焦点到一条渐近线的距离为．‎ ‎（1）求双曲线的方程；‎ ‎（2）设，分别为的左右顶点，为异于，一点，直线与分别交轴于，两点，求证：以线段为直径的圆经过两个定点．‎ ‎【解析】（1）设，因为离心率为2，所以，．‎ 所以的渐近线为，由，得．‎ 于是，，故的方程为．‎ ‎（2）方法一、设，，因为，，‎ 可得直线与方程为，．‎ 由题设，所以，，，‎ 中点坐标，于是圆的方程为．‎ 因为，所以圆的方程可化为．‎ 当时，，因此经过两个定点和．‎ 方法二、设，，因为，，‎ 可得直线与方程为，，‎ 由题设，所以，．‎ 设是圆上点，则，即，‎ 于是圆的方程为．‎ 因为，所以圆的方程可化为．‎ 当时，，因此经过两个定点和．‎ ‎26．（2019•浦东新区一模）已知双曲线的左、右焦点分别是、，左、右两顶点分别是、，弦和所在直线分别平行于轴与轴，线段的延长线与线段相交于点（如图）．‎ ‎（1）若是的一条渐近线的一个方向向量，试求的两渐近线的夹角；‎ ‎（2）若，，，，试求双曲线的方程；‎ ‎（3）在（1）的条件下，且，点与双曲线的顶点不重合，直线和直线与直线分别相交于点和，试问：以线段为直径的圆是否恒经过定点？若是，请求出定点的坐标；若不是，试说明理由．‎ ‎【解析】（1）双曲线的渐近线方程为：‎ 即，所以， ‎ 从而，，‎ 所以． ‎ ‎（2）设，，则由条件知：，，即．‎ 所以，，‎ 代入双曲线方程知：‎ 双曲线的方程：，‎ ‎（3）因为，所以，由（1）知，，所以的方程为：，‎ 令，，所以，，令，所以，，令，所以， ‎ 故以为直径的圆的方程为：，‎ 即，‎ 即， ‎ 若以为直径的圆恒经过定点 于是 所以圆过轴上两个定点和．‎ ‎27．（2018•临川区校级模拟）已知曲线是中心在原点，焦点在轴上的双曲线的右支，它的离心率刚好是其对应双曲线的实轴长，且一条渐近线方程是，线段是过曲线右焦点的一条弦，是弦的中点．‎ ‎（1）求曲线的方程；‎ ‎（2）当点在曲线上运动时，求点到轴距离的最小值；‎ ‎（3）若作出直线，使点在直线上的射影满足．当点在曲线上运动时，求的取值范围．【参考公式：若，为双曲线右支上的点，为右焦点，则．为离心率）】‎ ‎【解析】（1）设双曲线的方程为，‎ 由题意可得，，‎ 由，解得，，，‎ 即有曲线的方程是；‎ ‎（2）由（1）知，曲线的右焦点的坐标为，若弦的斜率存在，‎ 则弦的方程为：，代入双曲线方程得：‎ ‎，‎ 设点，， ，，‎ 由△，可得，显然成立；‎ ‎，，‎ 解得，‎ 点到轴距离：，‎ 而当弦的斜率不存在时，点到轴距离为．‎ 所以点到轴距离的最小值为2．‎ ‎（3）点在直线上的射影满足，，‎ 到直线的距离为①‎ 由焦半径公式，‎ 可得②‎ 将②代入①，得：，‎ ‎，且，‎ ‎．‎ ‎28．（2018•青岛二模）在平面直角坐标系中，点、分别为双曲线的左、右焦点，双曲线的离心率为2，点在双曲线上．不在轴上的动点与动点关于原点对称，且四边形的周长为．‎ ‎（1）求动点的轨迹方程；‎ ‎（2）已知动直线与轨迹交于不同的两点、，且与圆交于不同的两点、，当变化时，恒为定值，求常数的值．‎ ‎【解析】（1）点、分别为，，，‎ 由已知，‎ ‎，‎ ‎，，‎ 点在双曲线上，‎ ‎，‎ 则，‎ 即，‎ 解得，，‎ ‎，‎ 连接，‎ ‎，，‎ 四边形为平行四边形，‎ 四边形的周长为，‎ ‎，‎ 动点的轨迹是以，分别为左、右焦点，长轴长为的椭圆，（除去左右定点），‎ ‎（2）设，，，，由题意：得，‎ ‎，，‎ 又△，‎ ‎，‎ 又直线到定圆圆心的距离为，‎ ‎，‎ 为定值，‎ 为定值），‎ 化简得，‎ 且，‎ ‎，‎ 解得．‎ ‎29．（2018•浦东新区二模）已知双曲线．‎ ‎（1）求以右焦点为圆心，与双曲线的渐近线相切的圆的方程；‎ ‎（2）若经过点的直线与双曲线的右支交于不同两点、，求线段的中垂线在轴上截距的取值范围．‎ ‎【解析】（1）双曲线的右焦点为，，渐近线方程为：．‎ 到渐近线的距离为，‎ 圆的方程为．‎ ‎（2）设经过点的直线方程为，，，，，‎ 联立方程组，消去得：，‎ ‎，解得．‎ 的中点为，，‎ 线段的中垂线方程为：，‎ 令得截距．‎ 即线段的中垂线在轴上截距的取值范围是．‎ ‎30．（2018•青岛二模）在平面直角坐标系中，点、分别为双曲线的左、右焦点，双曲线的离心率为2，点在双曲线上．不在轴上的动点与动点关于原点对称，且四边形的周长为．‎ ‎（1）求动点的轨迹方程；‎ ‎（2）在动点的轨迹上有两个不同的点，、，，线段的中点为，已知点，在圆上，求的最大值，并判断此时的形状．‎ ‎【解析】（1）设，分别为，‎ 可得，，‎ 又点在双曲线上，，‎ 解得，．‎ 连接，，，四边形的周长为平行四边形．‎ 四边形，动点的轨迹是以点、分别为左右焦点的椭圆（除左右顶点），‎ 动点的轨迹方程；‎ ‎（2），，．‎ ‎．‎ 当时取最值，‎ 此时，为直角三角形．‎