2018版高考数学（理）（苏教版，江苏专用）大一轮教师文档讲义：第四章4-6正弦定理、余弦定理 21页

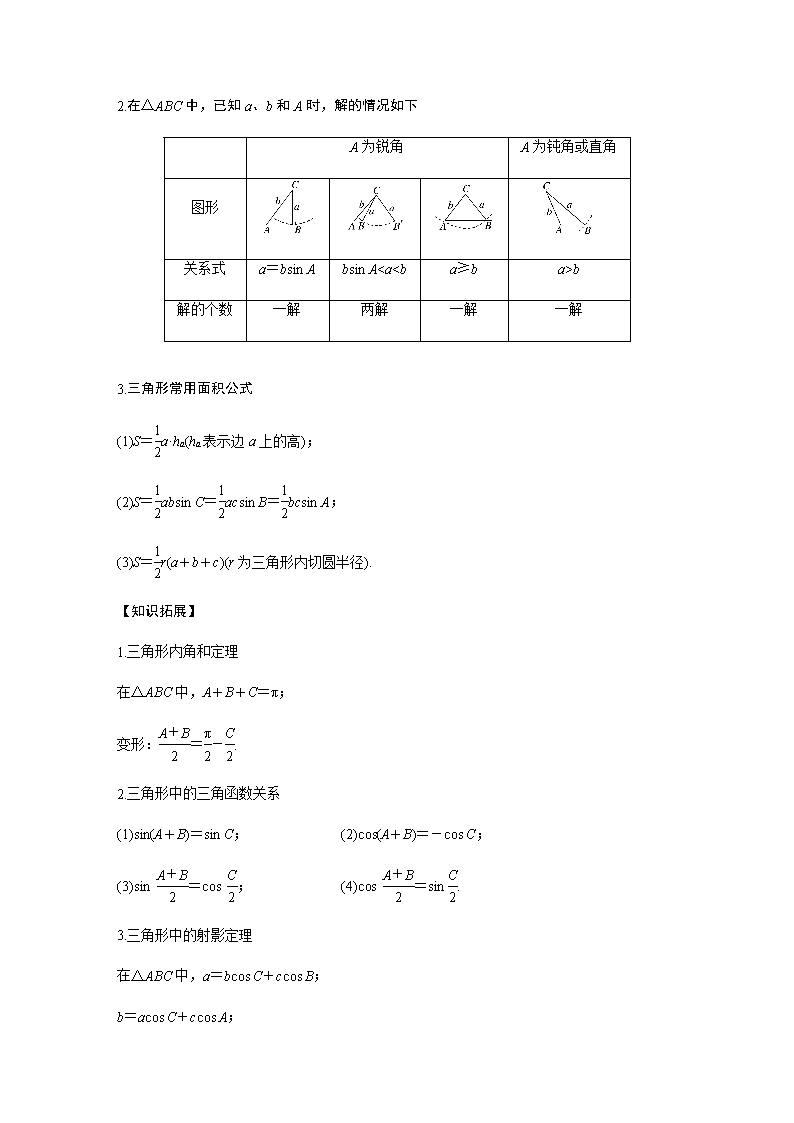
‎1.正弦定理、余弦定理 在△ABC中，若角A，B，C所对的边分别是a，b，c，R为△ABC外接圆半径，则 定理 正弦定理 余弦定理 内容 ＝＝＝2R a2＝b2＋c2－2bccos A；‎ b2＝c2＋a2－2cacos B；‎ c2＝a2＋b2－2abcos C 变形 ‎(1)a＝2Rsin A，‎ b＝2Rsin B，‎ c＝2Rsin C；‎ ‎(2)sin A＝，sin B＝，sin C＝；‎ ‎(3)a∶b∶c＝sin A∶sin B∶sin C；‎ ‎(4)asin B＝bsin A，‎ bsin C＝csin B，‎ asin C＝csin A cos A＝；‎ cos B＝；‎ cos C＝ ‎2.在△ABC中，已知a、b和A时，解的情况如下 A为锐角 A为钝角或直角 图形 关系式 a＝bsin A bsin Ab 解的个数 一解 两解 一解 一解 ‎3.三角形常用面积公式 ‎(1)S＝a·ha(ha表示边a上的高)；‎ ‎(2)S＝absin C＝acsin B＝bcsin A；‎ ‎(3)S＝r(a＋b＋c)(r为三角形内切圆半径).‎ ‎【知识拓展】‎ ‎1.三角形内角和定理 在△ABC中，A＋B＋C＝π；‎ 变形：＝－.‎ ‎2.三角形中的三角函数关系 ‎(1)sin(A＋B)＝sin C； (2)cos(A＋B)＝－cos C；‎ ‎(3)sin ＝cos ； (4)cos ＝sin .‎ ‎3.三角形中的射影定理 在△ABC中，a＝bcos C＋ccos B；‎ b＝acos C＋ccos A；‎ c＝bcos A＋acos B.‎ ‎【思考辨析】‎ 判断下列结论是否正确(请在括号中打“√”或“×”)‎ ‎(1)三角形中三边之比等于相应的三个内角之比.(　×　)‎ ‎(2)在△ABC中，若sin A＞sin B，则A＞B.(　√　)‎ ‎(3)在△ABC的六个元素中，已知任意三个元素可求其他元素.(　×　)‎ ‎(4)当b2＋c2－a2>0时，三角形ABC为锐角三角形.(　×　)‎ ‎(5)在△ABC中，＝.(　√　)‎ ‎(6)在三角形中，已知两边和一角就能求三角形的面积.(　√　)‎ ‎1.(教材改编)在△ABC中，a＝2，A＝30°，C＝45°，则△ABC的面积S△ABC＝ .‎ 答案　＋1‎ 解析　∵b＝＝＝＋，‎ ‎∴S△ABC＝absin C＝(＋)×＝＋1.‎ ‎2.(教材改编)在△ABC中，A＝60°，B＝75°，a＝10，则c＝ .‎ 答案　 解析　由A＋B＋C＝180°，知C＝45°，‎ 由正弦定理得＝，即＝，‎ ‎∴c＝.‎ ‎3.(教材改编)在△ABC中，A＝60°，AC＝2，BC＝，则AB＝ .‎ 答案　1‎ 解析　方法一　在△ABC中，根据余弦定理，即BC2＝AB2＋AC2－2·AB·AC·cos 60°，得()2＝AB2＋22－2AB×2×cos 60°，整理得AB2－2AB＋1＝0，解得AB＝1.‎ 方法二　在△ABC中，根据正弦定理，‎ 得＝，即＝，解得sin B＝1，‎ 因为B∈(0°，180°)，所以B＝90°，‎ 所以AB＝＝1.‎ ‎4.在△ABC中，角A，B，C对应的边分别为a，b，c，若A＝120°，a＝2，b＝，则B＝ .‎ 答案　 解析　∵A＝120°，a＝2，b＝，‎ ‎∴由正弦定理＝可得，‎ sin B＝sin A＝×＝.‎ ‎∵A＝120°，∴B＝30°，即B＝.‎ ‎5.(教材改编)在△ABC中，已知CB＝7，AC＝8，AB＝9，则AC边上的中线长为 .‎ 答案　7‎ 解析　由条件知cos A＝ ‎＝＝，‎ 设AC边上的中线长为x，由余弦定理知 x2＝()2＋AB2－2××ABcos A ‎＝42＋92－2×4×9×＝49，‎ ‎∴x＝7，故所求中线长为7.‎ 题型一　利用正弦定理、余弦定理解三角形 例1　(1)(2016·南京、盐城调研)在△ABC中，设a，b，c分别为角A，B，C的对边，若a＝5，A＝，cos B＝，则c＝ .‎ 答案　7‎ 解析　因为cos B＝，所以B∈(0，)，‎ 从而sin B＝，所以sin C＝sin(A＋B)＝sin Acos B＋cos Asin B＝×＋×＝，‎ 又由正弦定理得＝，即＝，解得c＝7.‎ ‎(2)(2016·四川)在△ABC中，角A，B，C所对的边分别是a，b，c，且＋＝.‎ ‎①证明：sin Asin B＝sin C；‎ ‎②若b2＋c2－a2＝bc，求tan B.‎ ‎①证明　根据正弦定理，可设 ＝＝＝k(k>0)，‎ 则a＝ksin A，b＝ksin B，c＝ksin C，‎ 代入＋＝中，有 ＋＝，变形可得 sin Asin B＝sin Acos B＋cos Asin B＝sin(A＋B).‎ 在△ABC中，由A＋B＋C＝π，有sin(A＋B)＝sin(π－C)＝sin C.所以sin Asin B＝sin C.‎ ‎②解　由已知，b2＋c2－a2＝bc，根据余弦定理，有 cos A＝＝.‎ 所以sin A＝＝.‎ 由①知，sin Asin B＝sin Acos B＋cos Asin B，‎ 所以sin B＝cos B＋sin B.‎ 故tan B＝＝4.‎ 思维升华　应用正弦、余弦定理的解题技巧 ‎(1)求边：利用公式a＝，b＝，c＝或其他相应变形公式求解.‎ ‎(2)求角：先求出正弦值，再求角，即利用公式sin A＝，sin B＝，sin C＝或其他相应变形公式求解.‎ ‎(3)已知两边和夹角或已知三边可利用余弦定理求解.‎ ‎(4)灵活利用式子的特点转化：如出现a2＋b2－c2＝λab形式用余弦定理，等式两边是关于边或角的正弦的齐次式用正弦定理.‎ ‎　(1)△ABC的三个内角A，B，C所对边的长分别为a，b，c，asin Asin B＋bcos2A＝a，则＝ .‎ ‎(2)在△ABC中，内角A，B，C的对边长分别为a，b，c，已知a2－c2＝b，且sin(A－C)＝2cos ‎ Asin C，则b＝ .‎ 答案　(1)　(2)2‎ 解析　(1)(边化角)‎ 由asin Asin B＋bcos2A＝a及正弦定理，得 sin Asin Asin B＋sin Bcos2A＝sin A，‎ 即sin B＝sin A，所以＝＝.‎ ‎(2)(角化边)‎ 由题意，得sin Acos C－cos Asin C＝2cos Asin C，‎ 即sin Acos C＝3cos Asin C，‎ 由正弦、余弦定理，得 a·＝3c·，‎ 整理得2(a2－c2)＝b2， ①‎ 又a2－c2＝b， ②‎ 联立①②得b＝2.‎ 题型二　和三角形面积有关的问题 例2　(2016·南通模拟)在△ABC中，角A，B，C所对的边分别为a，b，c，(a＋b－c)(a＋b＋c)＝ab.‎ ‎(1)求角C的大小；‎ ‎(2)若c＝2acos B，b＝2，求△ABC的面积.‎ 解　(1)在△ABC中，由(a＋b－c)(a＋b＋c)＝ab，‎ 得＝－，即cos C＝－.‎ 因为00，所以cos B<0，‎ 即B为钝角，所以△ABC为钝角三角形.‎ ‎(2)由3sin A＝5sin B及正弦定理得3a＝5b，‎ 故a＝b，c＝b.‎ 所以cos C＝＝－，即C＝π.‎ 从而△ABC为钝角三角形.‎ 引申探究 ‎1.例3(2)中，若将条件变为2sin Acos B＝sin C，判断△ABC的形状.‎ 解　∵2sin Acos B＝sin C＝sin(A＋B)，‎ ‎∴2sin Acos B＝sin Acos B＋cos Bsin A，‎ ‎∴sin(A－B)＝0，‎ 又A，B为△ABC的内角.‎ ‎∴A＝B，∴△ABC为等腰三角形.‎ ‎2.例3(2)中，若将条件变为a2＋b2－c2＝ab，且2cos Asin B＝sin C，判断△ABC的形状.‎ 解　∵a2＋b2－c2＝ab，∴cos C＝＝，‎ 又01.‎ ‎∴角B不存在，即满足条件的三角形不存在.‎ ‎5.在△ABC中，角A，B，C的对边分别为a，b，c，且cos2＝，则△ABC的形状是 三角形.‎ 答案　直角 解析　在△ABC中，∵cos2＝，‎ ‎∴＝＋，∴cos A＝，‎ ‎∴由余弦定理知cos A＝，‎ ‎∴＝，∴b2＋c2－a2＝2b2.‎ 即a2＋b2＝c2.故△ABC是直角三角形.‎ ‎6.(2016·连云港模拟)△ABC的内角A，B，C的对边分别为a，b，c，已知b＝2，B＝，C＝，则△ABC的面积为 .‎ 答案　＋1‎ 解析　∵b＝2，B＝，C＝.‎ 由正弦定理＝，‎ 得c＝＝＝2，‎ A＝π－(＋)＝π，‎ ‎∴sin A＝sin(＋)＝sin cos ＋cos sin ‎＝.‎ 则S△ABC＝bc·sin A＝×2×2×＝＋1.‎ ‎7.(2016·全国甲卷)△ABC的内角A，B，C的对边分别为a，b，c，若cos A＝，cos C＝，a＝1，则b＝ .‎ 答案　 解析　在△ABC中，由cos A＝，cos C＝，可得sin A＝，sin C＝，sin B＝sin(A＋C)＝sin Acos C＋cos A·sin C＝，由正弦定理得b＝＝.‎ ‎8.如图，正方形ABCD的边长为1，延长BA至E，使AE＝1，连结EC，ED，则sin∠CED＝ .‎ 答案　 解析　由题意得EB＝EA＋AB＝2，则在Rt△EBC中，EC＝＝＝.‎ 在△EDC中，∠EDC＝∠EDA＋∠ADC＝＋＝，‎ 由正弦定理得＝＝＝，‎ 所以sin∠CED＝·sin∠EDC＝·sin＝.‎ ‎9.在△ABC中，内角A，B，C所对的边分别为a，b，c，已知△ABC的面积为3，b－c＝2，cos A＝－，则a的值为 .‎ 答案　8‎ 解析　∵cos A＝－，0＜A＜π，∴sin A＝，‎ S△ABC＝bcsin A＝bc×＝3，∴bc＝24，‎ 又b－c＝2，∴b2－2bc＋c2＝4，b2＋c2＝52，‎ 由余弦定理得a2＝b2＋c2－2bccos A ‎＝52－2×24×＝64，‎ ‎∴a＝8.‎ ‎*10.在△ABC中，角A，B，C所对的边分别为a，b，c，且满足asin B＝bcos A.若a＝4，则△ABC周长的最大值为 .‎ 答案　12‎ 解析　由正弦定理＝，‎ 可将asin B＝bcos A转化为sin Asin B＝sin Bcos A.‎ 又在△ABC中，sin B>0，∴sin A＝cos A，‎ 即tan A＝.‎ ‎∵0×＋＝2.‎ ‎12.在△ABC中，角A，B，C所对的边分别为a，b，c，若∠B＝∠C且7a2＋b2＋c2＝4，则△ABC的面积的最大值为 .‎ 答案　 解析　由∠B＝∠C，得b＝c，代入7a2＋b2＋c2＝4，‎ 得7a2＋2b2＝4，即2b2＝4－7a2，‎ 由余弦定理，得cos C＝＝，‎ 所以sin C＝＝ ‎＝，‎ 则△ABC的面积 S＝absin C＝ab× ‎＝a＝ ‎＝× ‎≤×× ‎＝××4＝，‎ 当且仅当15a2＝8－15a2时取等号，此时a2＝.‎ 所以△ABC的面积的最大值为.‎ ‎13.四边形ABCD的内角A与C互补，AB＝1，BC＝3，CD＝DA＝2.‎ ‎(1)求C和BD；‎ ‎(2)求四边形ABCD的面积．‎ 解　(1)由题设A与C互补及余弦定理得 BD2＝BC2＋CD2－2BC·CDcos C＝13－12cos C， ①‎ BD2＝AB2＋DA2－2AB·DAcos A＝5＋4cos C． ②‎ 由①②得cos C＝，BD＝，‎ 因为C是三角形内角，故C＝60°.‎ ‎(2)四边形ABCD的面积 S＝AB·DAsin A＋BC·CDsin C ‎＝sin 60°‎ ‎＝2.‎ ‎14.(2015·湖南)设△ABC的内角A，B，C的对边分别为a，b，c，a＝btan A.‎ ‎(1)证明：sin B＝cos A；‎ ‎(2)若sin C－sin Acos B＝，且B为钝角，求A，B，C.‎ ‎(1)证明　由正弦定理知＝＝＝2R，‎ ‎∴a＝2Rsin A，b＝2Rsin B，代入a＝btan A得 sin A＝sin B·，又∵A∈(0，π)，∴sin A＞0，‎ ‎∴1＝，即sin B＝cos A.‎ ‎(2)解　由sin C－sin Acos B＝知，‎ sin(A＋B)－sin Acos B＝，∴cos Asin B＝.‎ 由(1)知，sin B＝cos A，∴cos2A＝，由于B是钝角，‎ 故A∈，∴cos A＝，A＝.‎ sin B＝，B＝，∴C＝π－(A＋B)＝.‎ ‎15.(2015·陕西)△ABC的内角A，B，C 所对的边分别为a，b，c.向量m＝(a，b)与n＝(cos A，sin B)平行.‎ ‎(1)求A；‎ ‎(2)若a＝，b＝2，求△ABC的面积.‎ 解　(1)因为m∥n，所以asin B－bcos A＝0，‎ 由正弦定理，得sin Asin B－sin Bcos A＝0，‎ 又sin B≠0，从而tan A＝，‎ 由于0＜A＜π，所以A＝.‎ ‎(2)方法一　由余弦定理，得a2＝b2＋c2－2bccos A，‎ 而由a＝，b＝2，A＝，‎ 得7＝4＋c2－2c，即c2－2c－3＝0，‎ 因为c＞0，所以c＝3，‎ 故△ABC的面积为S＝bcsin A＝.‎ 方法二　由正弦定理，得＝，‎ 从而sin B＝，‎ 又由a＞b，知A＞B，所以cos B＝，‎ 故sin C＝sin(A＋B)＝sin ‎＝sin Bcos ＋cos Bsin ＝.‎ 所以△ABC的面积为S＝absin C＝.‎