安徽省芜湖市第一中学高考物理一轮复习 第一章 第6讲 多过程常见问题（2）教案（通用） 5页

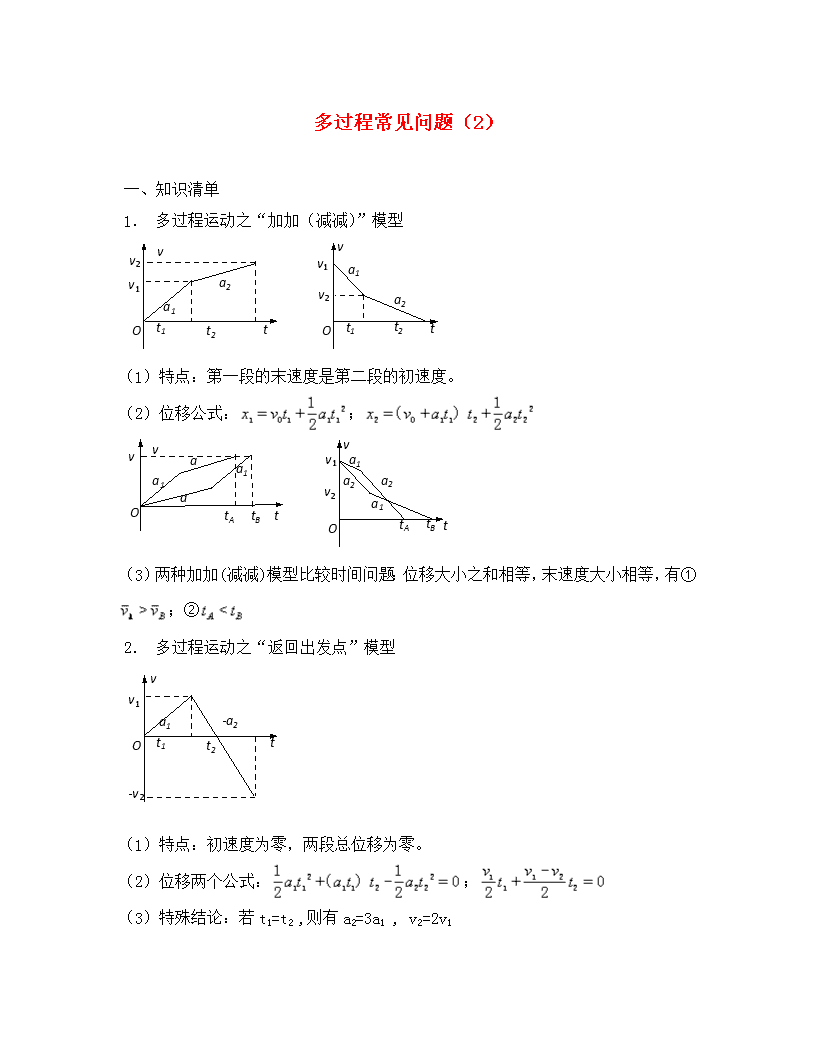
多过程常见问题（2） ‎ 一、知识清单 ‎1． 多过程运动之“加加（减减）”模型 t O v t2‎ t1‎ a2‎ a1‎ v1‎ v2‎ ‎ ‎t O v t2‎ t1‎ a2‎ a1‎ v1‎ v2‎ ‎（1）特点：第一段的末速度是第二段的初速度。‎ ‎（2）位移公式：；‎ t O v tB tA a2‎ a1‎ v a2‎ a1‎ ‎ ‎t O v tA tB a2‎ a1‎ v1‎ v2‎ a2‎ a1‎ ‎（3）两种加加(减减)模型比较时间问题：位移大小之和相等，末速度大小相等，有①；②‎ ‎2． 多过程运动之“返回出发点”模型 t O v t2‎ t1‎ ‎-a2‎ a1‎ v1‎ ‎-v2‎ ‎（1）特点：初速度为零，两段总位移为零。‎ ‎（2）位移两个公式：；‎ ‎（3）特殊结论：若t1=t2 ,则有a2=‎3a1 , v2=2v1‎ ‎3． 多过程运动之“减速为零，原路返回”模型 t O v t2‎ t1‎ a2‎ a1‎ v1‎ v2‎ ‎（1）特点：初（或末）速度为零，两段运动位移大小相等为x。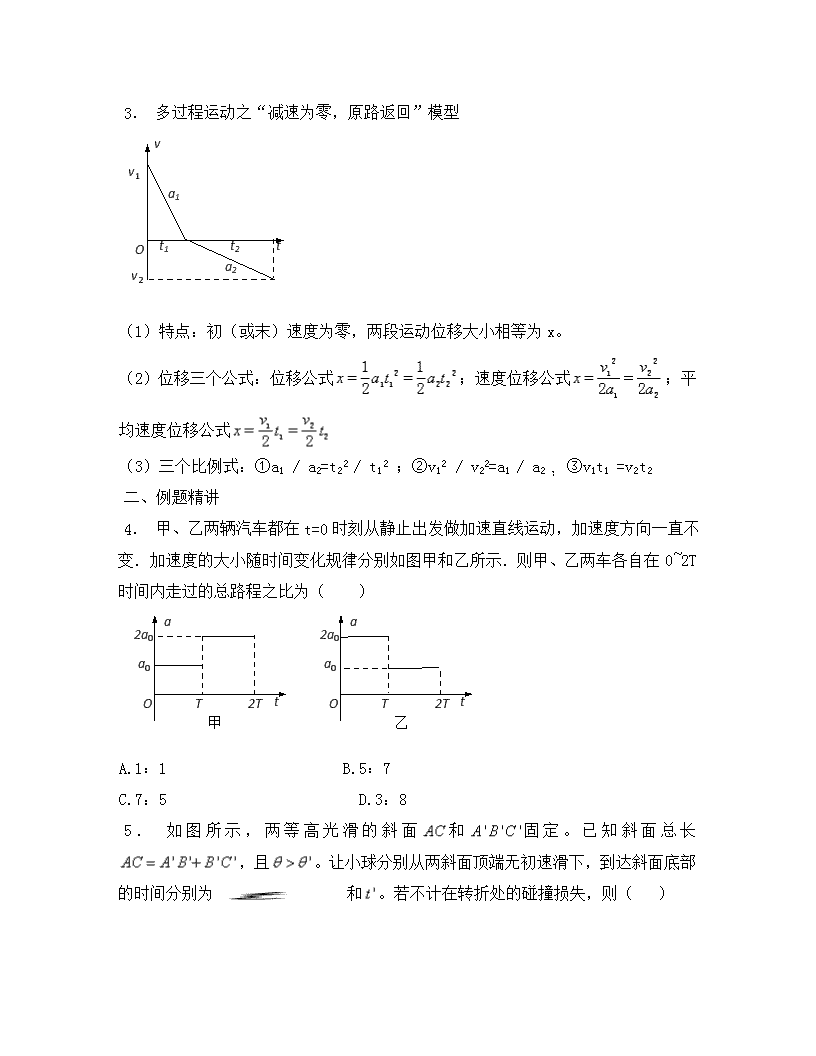‎ ‎（2）位移三个公式：位移公式；速度位移公式；平均速度位移公式 ‎（3）三个比例式：①a1 / a2=t22 / t12 ；②v12 / v22=a1 / a2 ； ③v1t1 =v2t2‎ 二、例题精讲 ‎4． 甲、乙两辆汽车都在t=0时刻从静止出发做加速直线运动，加速度方向一直不变．加速度的大小随时间变化规律分别如图甲和乙所示．则甲、乙两车各自在0~2T时间内走过的总路程之比为（　　）‎ t O a ‎2T T a0‎ ‎2a‎0‎ 甲 ‎ ‎t O a ‎2T T a0‎ ‎2a‎0‎ 乙 A.1：1           B.5：7‎ C.7：5            D.3：8‎ ‎5． 如图所示，两等高光滑的斜面和固定。已知斜面总长，且。让小球分别从两斜面顶端无初速滑下，到达斜面底部的时间分别为和。若不计在转折处的碰撞损失，则（ ）‎ A.> B.=‎ C.< D.不能确定 ‎6．一质点由静止做匀加速直线运动，加速度大小为a1，经过时间t后，开始做加速度大小为a2的匀减速直线运动，再经过t时间，恰好回到出发点．则两次的加速度大小之比a1：a2为（ ）‎ A．1：2 B．1：3‎ C．2：3 D．1：4‎ ‎7． （原创）已知一足够长的粗糙斜面，一滑块以初速度v0＝‎16 m/s从底端A点滑上斜面，经2 s滑至B点,在6s末又返回A点．其运动过程的v－t图象如图所示．则( )‎ A.AB之间的距离为16m B.滑块再次回到A点时的速度为‎8m/s C.上滑的加速度大小是下滑的4倍 D.上滑的加速度大小是下滑的2倍 ‎三、自我检测 ‎8． (多选)一物体做加速直线运动，依次通过A，B，C三点，AB=BC，物体在AB段的加速度为a1，所用时间为t1，在BC段的加速度为a2，所用时间为t2，且物体在B点的速度满足2vB=vA+vC，则（ ）‎ A.a1tB B．tA