2013年(全国卷II)(含答案)高考理科数学 20页

‎2013年普通高等学校招生全国统一考试（2新课标Ⅱ卷）‎ 数学(理)试题 一、选择题 ( 本大题 共 12 题, 共计 60 分)‎ ‎1．已知集合M＝{x|(x－1)2＜4，x∈R}，N＝{－1,0,1,2,3}，则M∩N＝(　　)．‎ A．{0,1,2} B．{－1,0,1,2} C．{－1,0,2,3} D．{0,1,2,3}‎ ‎2．设复数z满足(1－i)z＝2i，则z＝(　　)．‎ A．－1＋i B．－1－i C．1＋i D．1－i ‎3．等比数列{an}的前n项和为Sn.已知S3＝a2＋10a1，a5＝9，则a1＝(　　)．‎ A． B． C． D．‎ ‎4．已知m，n为异面直线，m⊥平面α，n⊥平面β.直线l满足l⊥m，l⊥n，lα，lβ，则(　　)．‎ A．α∥β且l∥α ‎ ‎ B．α⊥β且l⊥β C．α与β相交，且交线垂直于l ‎ D．α与β相交，且交线平行于l ‎5．已知(1＋ax)(1＋x)5的展开式中x2的系数为5，则a＝(　　)．‎ A．－4 B．－3 C．－2 D．－1‎ ‎6．执行下面的程序框图，如果输入的N＝10，那么输出的S＝(　　)．‎ A． B．‎ C． D．‎ ‎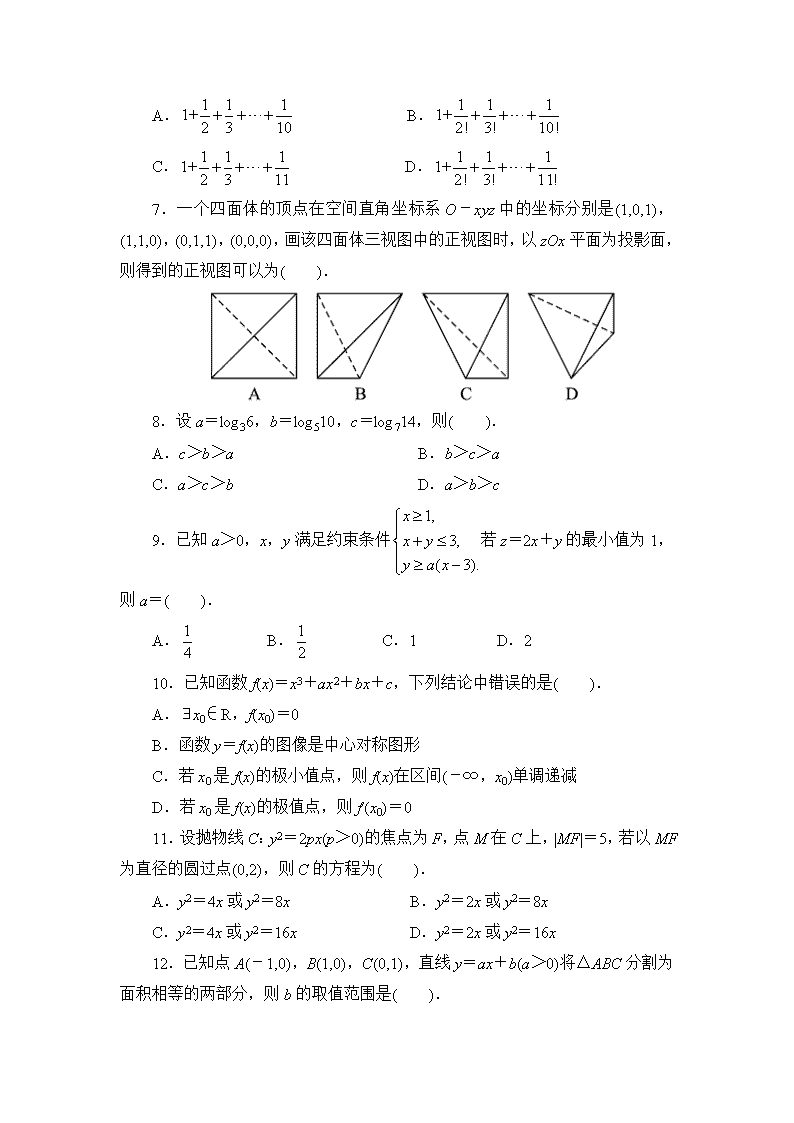7．一个四面体的顶点在空间直角坐标系O－xyz中的坐标分别是(1,0,1)，(1,1,0)，(0,1,1)，(0,0,0)，画该四面体三视图中的正视图时，以zOx平面为投影面，则得到的正视图可以为(　　)．‎ ‎8．设a＝log36，b＝log510，c＝log714，则(　　)．‎ A．c＞b＞a B．b＞c＞a C．a＞c＞b D．a＞b＞c ‎9．已知a＞0，x，y满足约束条件若z＝2x＋y的最小值为1，则a＝(　　)．‎ A． B． C．1 D．2‎ ‎10．已知函数f(x)＝x3＋ax2＋bx＋c，下列结论中错误的是(　　)．‎ A．x0∈R，f(x0)＝0‎ B．函数y＝f(x)的图像是中心对称图形 C．若x0是f(x)的极小值点，则f(x)在区间(－∞，x0)单调递减 D．若x0是f(x)的极值点，则f′(x0)＝0‎ ‎11．设抛物线C：y2＝2px(p＞0)的焦点为F，点M在C上，|MF|＝5，若以MF为直径的圆过点(0,2)，则C的方程为(　　)．‎ A．y2＝4x或y2＝8x B．y2＝2x或y2＝8x C．y2＝4x或y2＝16x D．y2＝2x或y2＝16x ‎12．已知点A(－1,0)，B(1,0)，C(0,1)，直线y＝ax＋b(a＞0)将△ABC分割为面积相等的两部分，则b的取值范围是(　　)．‎ A．(0,1) B． C． D．‎ 二、填空题：本大题共4小题，每小题5分．‎ ‎13．已知正方形ABCD的边长为2，E为CD的中点，则＝__________.‎ ‎14．从n个正整数1,2，…，n中任意取出两个不同的数，若取出的两数之和等于5的概率为，则n＝__________.‎ ‎15．设θ为第二象限角，若，则sin θ＋cos θ＝__________.‎ ‎16．等差数列{an}的前n项和为Sn，已知S10＝0，S15＝25，则nSn的最小值为__________．‎ 三、解答题：解答应写出文字说明，证明过程或演算步骤．‎ ‎17． (本小题满分12分)△ABC的内角A，B，C的对边分别为a，b，c，已知a＝bcos C＋csin B.‎ ‎(1)求B；‎ ‎(2)若b＝2，求△ABC面积的最大值．‎ ‎18． (本小题满分12分)如图，直三棱柱ABC－A1B1C1中，D，E分别是AB，BB1的中点，AA1＝AC＝CB＝.‎ ‎(1)证明：BC1∥平面A1CD；‎ ‎(2)求二面角D－A1C－E的正弦值．‎ ‎19． (本小题满分12分)经销商经销某种农产品，在一个销售季度内，每售出1 t该产品获利润500元，未售出的产品，每1 t亏损300元．根据历史资料，得到销售季度内市场需求量的频率分布直方图，如图所示．经销商为下一个销售季度购进了130 t该农产品．以X(单位：t,100≤X≤150)表示下一个销售季度内的市场需求量，T(单位：元)表示下一个销售季度内经销该农产品的利润．‎ ‎(1)将T表示为X的函数；‎ ‎(2)根据直方图估计利润T不少于57 000元的概率；‎ ‎(3)在直方图的需求量分组中，以各组的区间中点值代表该组的各个值，并以需求量落入该区间的频率作为需求量取该区间中点值的概率(例如：若需求量X∈[100,110)，则取X＝105，且X＝105的概率等于需求量落入[100,110)的频率)，求T的数学期望．‎ ‎20． (本小题满分12分)平面直角坐标系xOy中，过椭圆M：(a＞b＞0)右焦点的直线交M于A，B两点，P为AB的中点，且OP的斜率为.‎ ‎(1)求M的方程；‎ ‎(2)C，D为M上两点，若四边形ACBD的对角线CD⊥AB，求四边形ACBD面积的最大值．‎ ‎21． (本小题满分12分)已知函数f(x)＝ex－ln(x＋m)．‎ ‎(1)设x＝0是f(x)的极值点，求m，并讨论f(x)的单调性；‎ ‎(2)当m≤2时，证明f(x)＞0.‎ ‎22． (本小题满分10分)选修4—1：几何证明选讲 如图，CD为△ABC外接圆的切线，AB的延长线交直线CD于点D，E，F分别为弦AB与弦AC上的点，且BC·AE＝DC·AF，B，E，F，C四点共圆．‎ ‎(1)证明：CA是△ABC外接圆的直径；‎ ‎(2)若DB＝BE＝EA，求过B，E，F，C四点的圆的面积与△ABC外接圆面积的比值．‎ ‎23． (本小题满分10分)选修4—4：坐标系与参数方程 已知动点P，Q都在曲线C：(t为参数)上，对应参数分别为t＝α与t＝2α(0＜α＜2π)，M为PQ的中点．‎ ‎(1)求M的轨迹的参数方程；‎ ‎(2)将M到坐标原点的距离d表示为α的函数，并判断M的轨迹是否过坐标原点．‎ ‎24． (本小题满分10分)选修4—5：不等式选讲 设a，b，c均为正数，且a＋b＋c＝1，证明：‎ ‎(1)ab＋bc＋ac≤；‎ ‎(2).‎ ‎2013年普通高等学校招生全国统一考试（2新课标Ⅱ卷）‎ 数学(理)试题 答案解析: ‎ 一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．答案：A 解析：解不等式(x－1)2＜4，得－1＜x＜3，即M＝{x|－1＜x＜3}．而N＝{－1,0,1,2,3}，所以M∩N＝{0,1,2}，故选A.‎ ‎2．答案：A 解析：＝＝－1＋i.‎ ‎3．答案：C 解析：设数列{an}的公比为q，若q＝1，则由a5＝9，得a1＝9，此时S3＝27，而a2＋10a1＝99，不满足题意，因此q≠1.‎ ‎∵q≠1时，S3＝＝a1·q＋10a1，‎ ‎∴＝q＋10，整理得q2＝9.‎ ‎∵a5＝a1·q4＝9，即81a1＝9，∴a1＝.‎ ‎4．答案：D 解析：因为m⊥α，l⊥m，lα，所以l∥α.同理可得l∥β.‎ 又因为m，n为异面直线，所以α与β相交，且l 平行于它们的交线．故选D.‎ ‎5．答案：D 解析：因为(1＋x)5的二项展开式的通项为(0≤r≤5，r∈Z)，则含x2的项为＋ax·＝(10＋5a)x2，所以10＋5a＝5，a＝－1.‎ ‎6．答案：B 解析：由程序框图知，当k＝1，S＝0，T＝1时，T＝1，S＝1；‎ 当k＝2时，，；‎ 当k＝3时，，；‎ 当k＝4时，，；…；‎ 当k＝10时，，，k增加1变为11，满足k＞N，输出S，所以B正确．‎ ‎7．答案：A 解析：如图所示，该四面体在空间直角坐标系O－xyz的图像为下图：‎ 则它在平面zOx上的投影即正视图为，故选A.‎ ‎8．答案：D 解析：根据公式变形，，，，因为lg 7＞lg 5＞lg 3，所以，即c＜b＜a.故选D.‎ ‎9．答案：B 解析：由题意作出所表示的区域如图阴影部分所示，‎ 作直线2x＋y＝1，因为直线2x＋y＝1与直线x＝1的交点坐标为(1，－1)，结合题意知直线y＝a(x－3)过点(1，－1)，代入得，所以.‎ ‎10．答案：C 解析：∵x0是f(x)的极小值点，则y＝f(x)的图像大致如下图所示，则在(－∞，x0)上不单调，故C不正确．‎ ‎11．答案：C 解析：设点M的坐标为(x0，y0)，由抛物线的定义，得|MF|＝x0＋＝5，则x0＝5－.‎ 又点F的坐标为，所以以MF为直径的圆的方程为(x－x0)＋(y－y0)y＝0.‎ 将x＝0，y＝2代入得px0＋8－4y0＝0，即－4y0＋8＝0，所以y0＝4.‎ 由＝2px0，得，解之得p＝2，或p＝8.‎ 所以C的方程为y2＝4x或y2＝16x.故选C.‎ ‎12．答案：B 解析：情形1：直线y = ax +b与AC、BC相交时，如图所示，设MC = m, NC = n, ‎ 由条件知S△MNC = ⇒ mn = 1‎ 显然0 < n ≤ ⇒ m = ≥ 又知0 < m ≤, m ≠ n 所以≤ m ≤ 且m ≠ 1‎ D到AC、BC的距离为t, 则+ = + = 1‎ ‎⇒ t = ⇒= m + f (m ) = m + (≤ m ≤ 且m ≠ 1)的值域为(2, ] ⇒ 2 < ≤⇒ ≤ t < ‎ 因为b =1- CD =1- t ，所以1- < b ≤ 情形2：直线y = ax +b与AB、BC相交时，如图所示，‎ 易求得xM = - , yN = ,由条件知(1+ ) = 1‎ ‎⇒ = a M在线段OA上⇒0< <1 ⇒0 < a < b N在线段BC上⇒0< <1 ⇒b < 1‎ 解不等式：0 < < b得 < b < 综上：1- < b < 第Ⅱ卷 二、填空题：本大题共4小题，每小题5分．‎ ‎13．答案：2‎ 解析：以AB所在直线为x轴，AD所在直线为y轴建立平面直角坐标系，如图所示，则点A的坐标为(0,0)，点B 的坐标为(2,0)，点D的坐标为(0,2)，点E的坐标为(1,2)，则＝(1,2)，＝(－2,2)，所以.‎ ‎14．答案：8‎ 解析：从1,2，…，n中任取两个不同的数共有种取法，两数之和为5的有(1,4)，(2,3)2种，所以，即，解得n＝8.‎ ‎15．答案：‎ 解析：由，得tan θ＝，即sin θ＝cos θ.‎ 将其代入sin2θ＋cos2θ＝1，得.‎ 因为θ为第二象限角，所以cos θ＝，sin θ＝，sin θ＋cos θ＝.‎ ‎16．答案：－49‎ 解析：设数列{an}的首项为a1，公差为d，则S10＝＝10a1＋45d＝0，①‎ S15＝＝15a1＋105d＝25.②‎ 联立①②，得a1＝－3，，‎ 所以Sn＝.‎ 令f(n)＝nSn，则，.‎ 令f′(n)＝0，得n＝0或.‎ 当时，f′(n)＞0,时，f′(n)＜0，所以当时，f(n)取最小值，而n∈N＋，则f(6)＝－48，f(7)＝－49，所以当n＝7时，f(n)取最小值－49.‎ 三、解答题：解答应写出文字说明，证明过程或演算步骤．‎ ‎17．解：(1)由已知及正弦定理得 sin A＝sin Bcos C＋sin Csin B．①‎ 又A＝π－(B＋C)，故 sin A＝sin(B＋C)＝sin Bcos C＋cos Bsin C．②‎ 由①，②和C∈(0，π)得sin B＝cos B，‎ 又B∈(0，π)，所以.‎ ‎(2)△ABC的面积.‎ 由已知及余弦定理得4＝a2＋c2－.‎ 又a2＋c2≥2ac，故，当且仅当a＝c时，等号成立．‎ 因此△ABC面积的最大值为.‎ ‎18．解：(1)连结AC1交A1C于点F，则F为AC1中点．‎ 又D是AB中点，连结DF，则BC1∥DF.‎ 因为DF⊂平面A1CD，BC1平面A1CD，‎ 所以BC1∥平面A1CD.‎ ‎(2)由AC＝CB＝得，AC⊥BC.‎ 以C为坐标原点，的方向为x轴正方向，建立如图所示的空间直角坐标系C－xyz.‎ 设CA＝2，则D(1,1,0)，E(0,2,1)，A1(2,0,2)，＝(1,1,0)，＝(0,2,1)，＝(2,0,2)．‎ 设n＝(x1，y1，z1)是平面A1CD的法向量，‎ 则即可取n＝(1，－1，－1)．‎ 同理，设m是平面A1CE的法向量，‎ 则可取m＝(2,1，－2)．‎ 从而cos〈n，m〉＝，故sin〈n，m〉＝.‎ 即二面角D－A1C－E的正弦值为.‎ ‎19．解：(1)当X∈[100,130)时，T＝500X－300(130－X)＝800X－39 000，‎ 当X∈[130,150]时，T＝500×130＝65 000.‎ 所以 ‎(2)由(1)知利润T不少于57 000元当且仅当120≤X≤150.‎ 由直方图知需求量X∈[120,150]的频率为0.7，所以下一个销售季度内的利润T不少于57 000元的概率的估计值为0.7.‎ ‎(3)依题意可得T的分布列为 T ‎45 000‎ ‎53 000‎ ‎61 000‎ ‎65 000‎ P ‎0.1‎ ‎0.2‎ ‎0.3‎ ‎0.4‎ 所以ET＝45 000×0.1＋53 000×0.2＋61 000×0.3＋65 000×0.4＝59 400.‎ ‎20．解：(1)设A(x1，y1)，B(x2，y2)，P(x0，y0)，‎ 则，，，‎ 由此可得.‎ 因为x1＋x2＝2x0，y1＋y2＝2y0，，所以a2＝2b2.‎ 又由题意知，M的右焦点为(，0)，故a2－b2＝3.‎ 因此a2＝6，b2＝3.所以M的方程为.‎ ‎(2)由 解得或 因此|AB|＝.‎ 由题意可设直线CD的方程为 y＝，‎ 设C(x3，y3)，D(x4，y4)．‎ 由得3x2＋4nx＋2n2－6＝0.‎ 于是x3,4＝.因为直线CD的斜率为1，‎ 所以|CD|＝.由已知，四边形ACBD的面积.‎ 当n＝0时，S取得最大值，最大值为.‎ 所以四边形ACBD面积的最大值为.‎ ‎21．解：(1)f′(x)＝.‎ 由x＝0是f(x)的极值点得f′(0)＝0，所以m＝1.‎ 于是f(x)＝ex－ln(x＋1)，定义域为(－1，＋∞)，f′(x)＝.‎ 函数f′(x)＝在(－1，＋∞)单调递增，且f′(0)＝0.‎ 因此当x∈(－1,0)时，f′(x)＜0；‎ 当x∈(0，＋∞)时，f′(x)＞0.‎ 所以f(x)在(－1,0)单调递减，在(0，＋∞)单调递增．‎ ‎(2)当m≤2，x∈(－m，＋∞)时，ln(x＋m)≤ln(x＋2)，故只需证明当m＝2时，f(x)＞0.‎ 当m＝2时，函数f′(x)＝在(－2，＋∞)单调递增．‎ 又f′(－1)＜0，f′(0)＞0，‎ 故f′(x)＝0在(－2，＋∞)有唯一实根x0，且x0∈(－1,0)．‎ 当x∈(－2，x0)时，f′(x)＜0；‎ 当x∈(x0，＋∞)时，f′(x)＞0，从而当x＝x0时，f(x)取得最小值．‎ 由f′(x0)＝0得＝，ln(x0＋2)＝－x0，‎ 故f(x)≥f(x0)＝＋x0＝＞0.‎ 综上，当m≤2时，f(x)＞0.‎ 请考生在第22、23、24题中任选择一题作答，如果多做，则按所做的第一题计分，做答时请写清题号．‎ ‎22．解：(1)因为CD为△ABC外接圆的切线，‎ 所以∠DCB＝∠A，由题设知，‎ 故△CDB∽△AEF，所以∠DBC＝∠EFA.‎ 因为B，E，F，C四点共圆，所以∠CFE＝∠DBC，‎ 故∠EFA＝∠CFE＝90°.所以∠CBA＝90°，因此CA是△ABC外接圆的直径．‎ ‎(2)连结CE，因为∠CBE＝90°，所以过B，E，F，C四点的圆的直径为CE，由DB＝BE，有CE＝DC，又BC2＝DB·BA＝2DB2，所以CA2＝4DB2＋BC2＝6DB2.‎ 而DC2＝DB·DA＝3DB2，故过B，E，F，C四点的圆的面积与△ABC外接圆面积的比值为.‎ ‎23．解：(1)依题意有P(2cos α，2sin α)，Q(2cos 2α，2sin 2α)，‎ 因此M(cos α＋cos 2α，sin α＋sin 2α)．‎ M的轨迹的参数方程为(α为参数，0＜α＜2π)．‎ ‎(2)M点到坐标原点的距离 ‎(0＜α＜2π)．‎ 当α＝π时，d＝0，故M的轨迹过坐标原点．‎ ‎24．解：（Ⅰ）由a2 + b2 ≥2ab，b2 + c2 ≥2bc，a2 + c2 ≥2ac得 ‎ a2 + b2 + c2≥ab + bc + ac ‎ ⇒ (a + b + c)2 = (a2 + b2 + c2) + 2(ab + bc + ac) ≥3(ab + bc + ac) ‎ ‎ ⇒ 1≥3(ab + bc + ac)‎ ‎ ⇒ab + bc + ac ≤ .‎ ‎（Ⅱ）证法一：因为 + b ≥2a，+ c ≥2b，+ a ≥2c 所以 ( + + )+(a + b + c) ≥ 2(a + b + c)‎ ‎⇒ + + + 1 ≥ 2⇒ + + ≥1‎ 证法二：由柯西不等式得：( + + )( b + c + a)≥ (a + b + c)2‎ ‎⇒ + + ≥1‎