2015届高考数学教材知识点复习导学案47.doc 5页

www.ks5u.com ‎【学习目标】‎ ‎1．了解构成函数的要素，会求一些简单函数的定义域和值域．‎ ‎2．了解简单的分段函数，并能简单应用．‎ 预 习 案 ‎1．函数的定义域 ‎(1)求定义域的步骤：‎ ‎①写出使函数式有意义的不等式(组)；②解不等式(组)；③写出函数定义域．(注意用区间或集合的形式写出)‎ (2) 函数f(x)＝x0的定义域为 ；‎ (3) 指数函数的定义域为 ；对数函数的定义域为 ．‎ ‎2．函数的值域 ‎(1)y＝kx＋b(k≠0)的值域是 ．‎ ‎(2)y＝ax2＋bx＋c(a≠0)的值域是：当a>0时，值域为 ；当a<0时，值域为 ．‎ ‎(3)y＝(k≠0)的值域是 ．(4)y＝ax(a>0且a≠1)的值域是 ．‎ ‎ (5)y＝logax(a>0且a≠1)的值域是 ．‎ ‎【预习自测】‎ ‎1．函数y＝的定义域是 (　　)‎ A．(－∞，2) B．(2，＋∞) C．(2,3)∪(3，＋∞) D．(2,4)∪(4，＋∞)‎ ‎2．若函数y＝f(x)的定义域是，则函数g(x)＝的定义域是 (　　)‎ A． B． D．(0,1)‎ ‎3．函数y＝log0.3(x2＋4x＋5)的值域为________．‎ ‎4．函数y＝的值域为________．‎ ‎ ‎ ‎ 探 究 案 ‎ 题型一 函数的定义域 例1.　(1)函数y＝的定义域为 ．‎ ‎ ‎ ‎(2)函数y＝(a>0且a≠1)的定义域为 ．‎ ‎(3)函数f(x)＝的定义域为 ．‎ 探究1.求函数y＝＋lgcosx的定义域．‎ 例2.　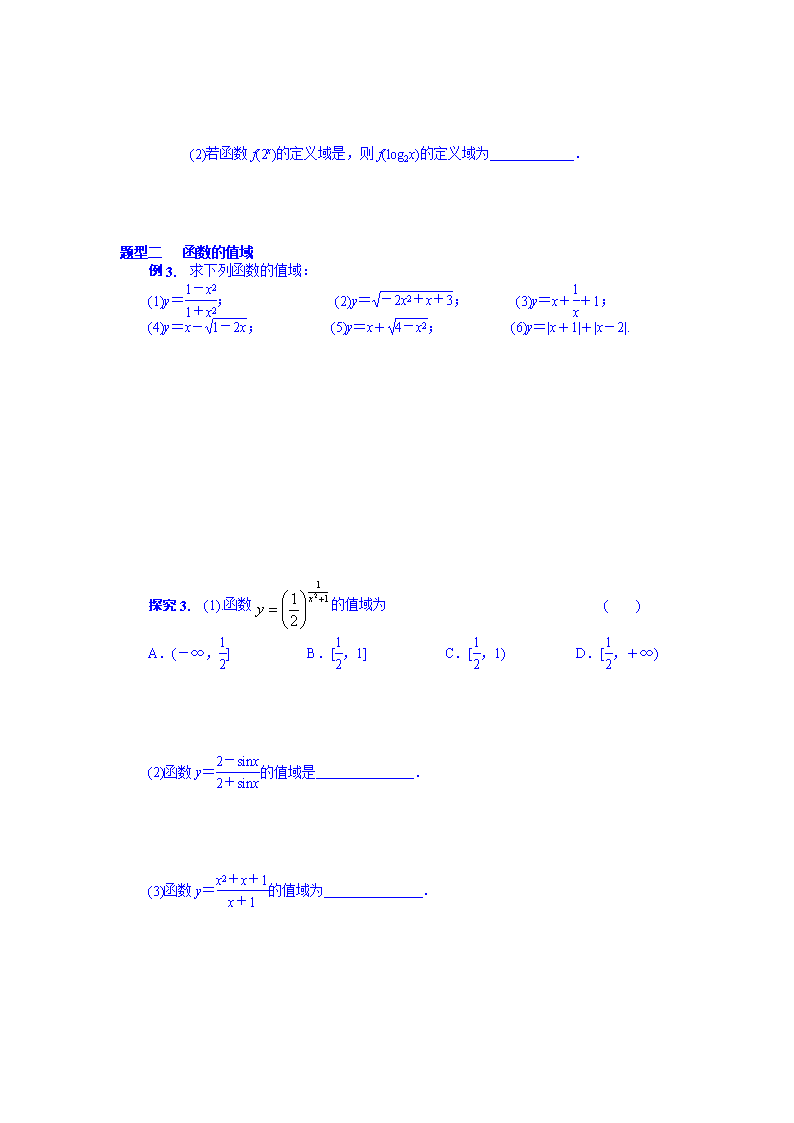(1)已知y＝f(x)的定义域为，求y＝f(3x－1)的定义域．‎ ‎ ‎ ‎ (2)已知y＝f(log2x)的定义域为，求y＝f(x)的定义域．‎ 探究2.(1)已知函数f(x)的定义域为(－1,0)，则函数f(2x＋1)的定义域为 ．‎ ‎ ‎ ‎ (2)若函数f(2x)的定义域是，则f(log2x)的定义域为 ．‎ 题型二 函数的值域 例3.　求下列函数的值域：‎ ‎(1)y＝； (2)y＝； (3)y＝x＋＋1；‎ ‎(4)y＝x－； (5)y＝x＋； (6)y＝|x＋1|＋|x－2|.‎ 探究3. (1).函数的值域为 (　　)‎ A．(－∞，] B．[，1] C．[，1) D．[，＋∞)‎ ‎(2)函数y＝的值域是 ．‎ ‎(3)函数y＝的值域为 ．‎ 题型三 定义域与值域的应用 例4.　已知函数f(x)＝lg．‎ ‎(1)若f(x)的定义域为R，求实数a的取值范围；‎ ‎(2)若f(x)的值域为R，求实数a的取值范围．‎ 探究4.已知函数f(x)＝x2－4ax＋2a＋6，x∈R.‎ ‎(1)若函数的值域为 ‎ 我的学习总结：‎ ‎（1）我对知识的总结 .‎ ‎（2）我对数学思想及方法的总结 ‎ ‎ ‎ ‎ ‎