高考总复习数学理精练三角函数解三角形单元检测附答案答案含详解 9页

‎2013年高考第一轮复习数学北师(江西版)理第四章三角函数、解三角形单元检测 ‎ (时间：120分钟　满分：150分)‎ 一、选择题(本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的)‎ ‎1．已知角α的终边过点P(－‎8m，－6sin 30°)且cos α＝－，则m的值为(　　)． ‎ A．－ B． C．－ D． ‎2．函数f(x)＝sin＋asin(a＞0)的一条对称轴方程为x＝，则a等于(　　)． ‎ A．1 B. 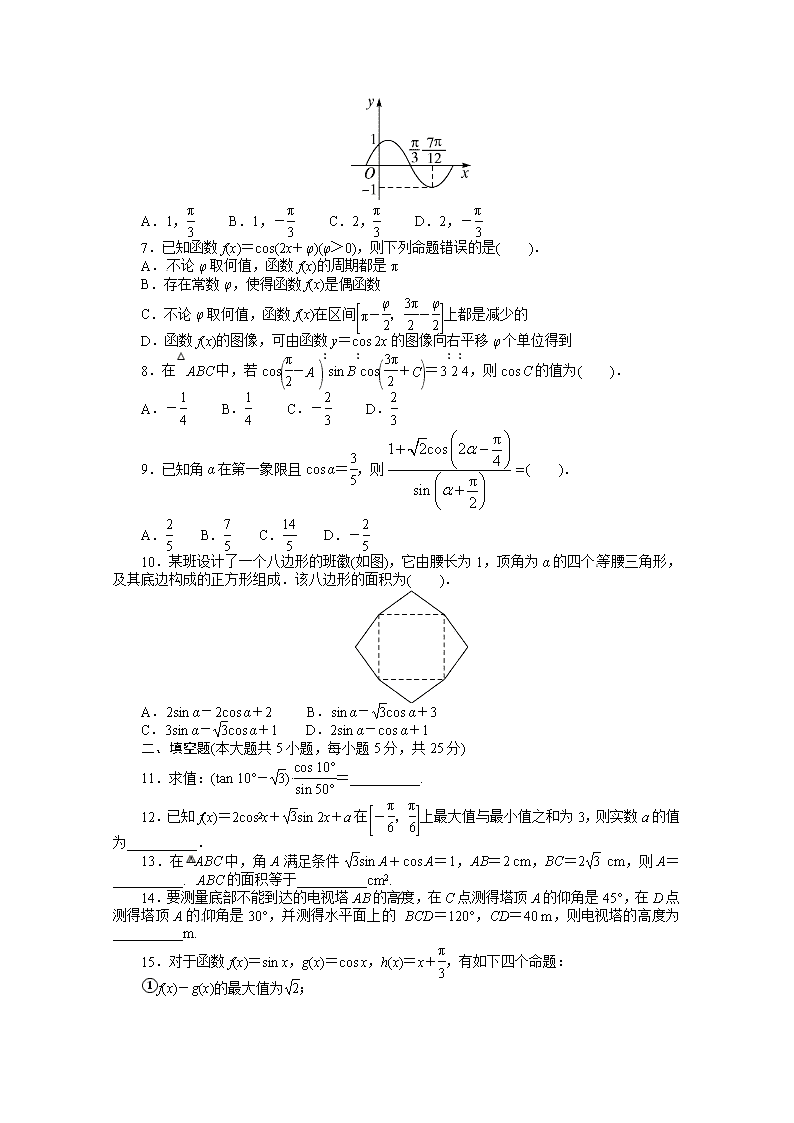C．2 D．3‎ ‎3．函数y＝1－2sin2是(　　)．‎ A．最小正周期为π的偶函数 B．最小正周期为π的奇函数 C．最小正周期为的偶函数 D．最小正周期为的奇函数 ‎4．已知f(x)＝cos的图像与y＝1的图像的两相邻交点间的距离为π，要得到y＝f(x)的图像，只需把y＝sin ωx的图像(　　)．‎ A．向左平移π个单位 B．向右平移π个单位 C．向左平移π个单位 D．向右平移π个单位 ‎5．函数y＝sin在区间的简图是(　　)．‎ ‎6．(2011福建三明模拟)把函数y＝sin(ωx＋φ)的图像向左平移个单位长度，所得的曲线的一部分图像如图所示，则ω，φ的值分别是(　　)．‎ A．1， B．1，－ C．2， D．2，－ ‎7．已知函数f(x)＝cos(2x＋φ)(φ＞0)，则下列命题错误的是(　　)．‎ A．不论φ取何值，函数f(x)的周期都是π B．存在常数φ，使得函数f(x)是偶函数 C．不论φ取何值，函数f(x)在区间上都是减少的 D．函数f(x)的图像，可由函数y＝cos 2x的图像向右平移φ个单位得到 ‎8．在△ABC中，若cos∶sin B∶cos＝3∶2∶4，则cos C的值为(　　)．‎ A．－ B． C．－ D． ‎9．已知角α在第一象限且cos α＝，则(　　)．‎ A． B． C． D．－ ‎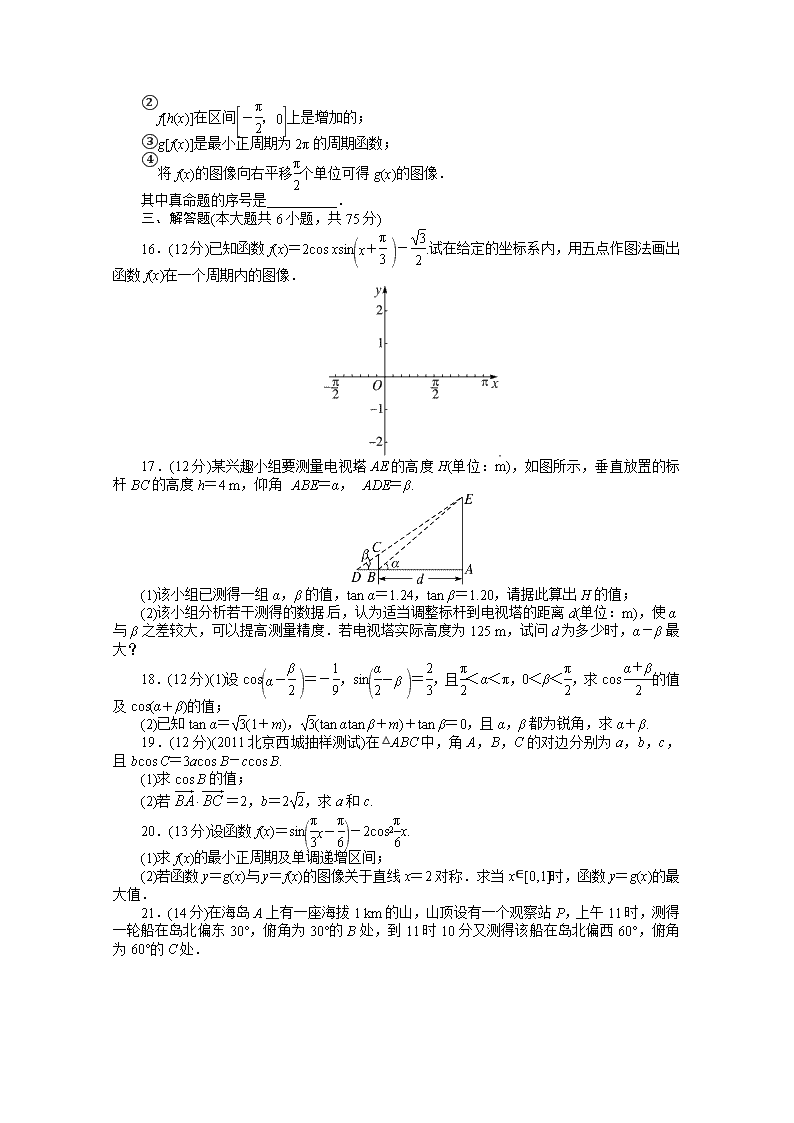10．某班设计了一个八边形的班徽(如图)，它由腰长为1，顶角为α的四个等腰三角形，及其底边构成的正方形组成．该八边形的面积为(　　)．‎ A．2sin α－2cos α＋2 B．sin α－cos α＋3‎ C．3sin α－cos α＋1 D．2sin α－cos α＋1‎ 二、填空题(本大题共5小题，每小题5分，共25分)‎ ‎11．求值：(tan 10°－)·＝__________.‎ ‎12．已知f(x)＝2cos2x＋sin 2x＋a在上最大值与最小值之和为3，则实数a的值为__________．‎ ‎13．在△ABC中，角A满足条件sin A＋cos A＝1，AB＝‎2 cm，BC＝‎2 cm，则A＝__________.△ABC的面积等于__________cm2.‎ ‎14．要测量底部不能到达的电视塔AB的高度，在C点测得塔顶A的仰角是45°，在D点测得塔顶A的仰角是30°，并测得水平面上的∠BCD＝120°，CD＝‎40 m，则电视塔的高度为__________m.‎ ‎15．对于函数f(x)＝sin x，g(x)＝cos x，h(x)＝x＋，有如下四个命题：‎ ‎①f(x)－g(x)的最大值为；‎ ‎②f[h(x)]在区间上是增加的；‎ ‎③g[f(x)]是最小正周期为2π的周期函数；‎ ‎④将f(x)的图像向右平移个单位可得g(x)的图像．‎ 其中真命题的序号是__________．‎ 三、解答题(本大题共6小题，共75分)‎ ‎16．(12分)已知函数f(x)＝2cos xsin－.试在给定的坐标系内，用五点作图法画出函数f(x)在一个周期内的图像．‎ ‎17．(12分)某兴趣小组要测量电视塔AE的高度H(单位：m)，如图所示，垂直放置的标杆BC的高度h＝‎4 m，仰角∠ABE＝α，∠ADE＝β.‎ ‎(1)该小组已测得一组α，β的值，tan α＝1.24，tan β＝1.20，请据此算出H的值；‎ ‎(2)该小组分析若干测得的数据后，认为适当调整标杆到电视塔的距离d(单位：m)，使α与β之差较大，可以提高测量精度．若电视塔实际高度为‎125 m，试问d为多少时，α－β最大？ ‎ ‎18．(12分)(1)设cos＝－，sin＝，且＜α＜π，0＜β＜，求cos的值及cos(α＋β)的值；‎ ‎(2)已知tan α＝(1＋m)，(tan αtan β＋m)＋tan β＝0，且α，β都为锐角，求α＋β.‎ ‎19．(12分)(2011北京西城抽样测试)在△ABC中，角A，B，C的对边分别为a，b，c，且bcos C＝3acos B－ccos B.‎ ‎(1)求cos B的值；‎ ‎(2)若＝2，b＝2，求a和c.‎ ‎20．(13分)设函数f(x)＝sin－2cos2x.‎ ‎(1)求f(x)的最小正周期及单调递增区间；‎ ‎(2)若函数y＝g(x)与y＝f(x)的图像关于直线x＝2对称．求当x∈[0,1]时，函数y＝g(x)的最大值．‎ ‎21．(14分)在海岛A上有一座海拔‎1 km的山，山顶设有一个观察站P，上午11时，测得一轮船在岛北偏东30°，俯角为30°的B处，到11时10分又测得该船在岛北偏西60°，俯角为60°的C处．‎ ‎(1)求船的航行速度；‎ ‎(2)经过一段时间后，船到达海岛的正西方向的D处，问此时船距岛A有多远？‎ 参考答案 一、选择题 ‎1．B　解析：∵|OP|＝，且cos α＝＝－，‎ ‎∴m＞0且＝，∴m＝.‎ ‎2．B　解析：∵该函数的一条对称轴方程为x＝，‎ ‎∴f(0)＝f(π)，即sin－asin＝－sin＋asin，解得a＝.故选B.‎ ‎3．B　解析：由已知得y＝cos 2＝cos＝sin 2x，因此函数y＝1－2sin2是最小正周期为π的奇函数．故选B.‎ ‎4．A　解析：依题意，y＝f(x)的最小正周期为π，故ω＝2，‎ 因为y＝cos＝sin＝sin＝sin，‎ 所以把y＝sin 2x的图像向左平移个单位即可得到y＝cos的图像．故选A.‎ ‎5．A　解析：由－≤x≤π得，－≤2x－≤，故当2x－＝－或，即x＝－或时函数取得最小值；当2x－＝0，即x＝时y＝0；当2x－＝，即x＝时函数取得最大值．结合图像可知A满足以上条件．‎ ‎6．D　解析：y＝sin(ωx＋φ)向左平移个单位长度y＝sin，‎ ‎∴T＝＝×4，ω＝2，‎ 当x＝π时，2＋φ＝2kπ＋π，k∈Z，∴φ＝2kπ－(k∈Z)，‎ ‎∵|φ|＜，∴φ＝－.‎ ‎7．D　解析：选项A，根据T＝＝π，不论φ取何值，函数f(x)的周期都是π；选项B，当φ＝kπ(k∈Z)时，函数f(x)是偶函数；选项C，当x∈时，2x＋φ∈[2π，3π]，y＝cos(2x＋φ)为减函数；选项D，y＝cos 2x的图像向右平移φ个单位得到y＝cos(2x－2φ)的图像，D错．‎ ‎8．A　解析：根据正弦定理sin A＝，sin B＝，sin C＝，由cos∶sin B∶cos＝3∶2∶4，‎ 可得sin A∶sin B∶sin C＝a∶b∶c＝3∶2∶4，∴cos C＝－.故选A.‎ ‎9．C　解析：∵cos α＝且α在第一象限，∴sin α＝.原式＝‎ ‎＝ ‎＝＝2(cos α＋sin α) ‎ ‎＝2＝.故选C.‎ ‎10．A　解析：每个等腰三角形的底边长为2sin，底边上的高为cos，所以该八边形的面积为4×·2sin·cos＋4sin2＝2sin α－2cos α＋2.故选A.‎ 二、填空题 ‎11．－2　解析：原式 ‎＝· ‎＝＝ ‎＝－2.‎ ‎12．0　解析：f(x)＝1＋cos 2x＋sin 2x＋a＝2sin＋a＋1.‎ ‎∵x∈，‎ ‎∴2x＋∈.‎ ‎∴－≤sin≤1.‎ 即 ‎∴‎2a＋3＝3，∴a＝0.‎ ‎13．　　解析：由sin A＋cos A＝1，‎ 得2sin＝1，A＝π，‎ 由＝，得sin C＝＝＝，C＝.则B＝，S＝AB×BCsin B＝(cm2)．‎ ‎14．40　解析：如图，设电视塔AB高为x m，‎ 则在Rt△ABC中，由∠ACB＝45°得BC＝x.‎ 在Rt△ADB中，∠ADB＝30°，‎ ‎∴BD＝x.‎ 在△BDC中，由余弦定理得，‎ BD2＝BC2＋CD2－2BC·CD·cos 120°，‎ 即(x)2＝x2＋402－2·x·40·cos 120°，解得x＝40，‎ ‎∴电视塔高为‎40 m.‎ ‎15．①②　解析：f(x)－g(x)＝sin x－cos x＝sin≤，‎ 故①正确；当x∈时，x＋∈，‎ 函数f[h(x)]＝sin为增函数，故②正确；函数g[f(x)]＝cos(sin x ‎)的最小正周期为π，故③错误；将f(x)的图像向左平移个单位可得g(x)的图像，故④错误．‎ 三、解答题惠生活www.huizhous.com 观影园www.gypark.com爱尚家居www.33203.com 嘟嘟园www.ddpark.com迅播影院www.gvod.us请支持我们，会有更多资源给大家 ‎16．解：∵f(x)＝2cos x·sin－ ‎＝2cos x·－ ‎＝sin 2x＋cos2x－ ‎＝sin 2x＋·－ ‎＝sin 2x＋cos 2x＝sin，‎ ‎∴T＝π.‎ 列表 x＝－ ‎－ π π t＝2x＋ ‎0‎ π π ‎2π sin t ‎0‎ ‎1‎ ‎0‎ ‎－1‎ ‎0‎ ‎17．解：(1)由AB＝，BD＝，AD＝及AB＋BD＝AD，‎ 得＋＝，‎ 解得H＝＝＝124.‎ 因此，算出的电视塔的高度H是‎124 m.‎ ‎(2)由题设知d＝AB，得tan α＝.‎ 由AB＝AD－BD＝－，‎ 得tan β＝.‎ 所以tan(α－β)＝ ‎＝≤，‎ 当且仅当d＝，即d＝＝＝55时，上式取等号，所以当d＝55时，tan(α－β)最大． ‎ 因为0＜β＜α＜，则0＜α－β＜，‎ 所以当d＝55时，α－β最大．‎ 故所求的d是‎55 m.‎ ‎18．解：(1)∵＜α＜π，0＜β＜，‎ ‎∴＜α－＜π，－＜－β＜.‎ ‎∴sin＝＝，cos＝＝，‎ ‎∴cos＝cos ‎＝coscos＋sinsin＝，‎ ‎∴cos(α＋β)＝2cos2－1＝－.‎ ‎(2)由已知可得tan α＝＋m，①‎ tan β＝－tan αtan β－m，②‎ ‎∴①＋②可得tan α＋tan β＝(1－tan αtan β)，‎ ‎∴＝tan(α＋β)＝，‎ 又∵0＜α＜，0＜β＜.‎ ‎∴0＜α＋β＜π，∴α＋β＝.‎ ‎19．解：(1)由正弦定理得a＝2Rsin A，b＝2Rsin B，c＝2Rsin C，‎ ‎∴sin Bcos C＝3sin Acos B－sin Ccos B.‎ 可得sin Bcos C＋sin Ccos B＝3sin Acos B，∴sin(B＋C)＝3sin Acos B．可得sin A＝3sin Acos B.‎ 又sin A≠0，∴cos B＝.‎ ‎(2)由＝2，得accos B＝2，可得ac＝6.由b2＝a2＋c2－2accos B，可得a2＋c2＝12，∴(a－c)2＝0，得a＝c，∴a＝c＝.‎ ‎20．解：(1)∵f(x)＝sinx－‎ cosx－1＝sin－1，‎ ‎∴T＝＝6，由－＋2kπ≤x－≤＋2kπ，k∈Z，‎ 得－＋6k≤x≤＋6k，k∈Z.‎ 所以函数f(x)的最小正周期为6，‎ 单调递增区间为，k∈Z.‎ ‎(2)∵函数y＝g(x)与y＝f(x)的图像关于直线x＝2对称，∴当x∈[0,1]时，函数y＝g(x)的最大值即为x∈[3,4]时y＝f(x)的最大值，‎ 此时x－∈，sin∈，f(x)∈，即此时函数y＝g(x)的最大值为.‎ ‎21．解：(1)在Rt△PAB中，∠APB＝60°，PA＝1，∴AB＝(千米)．‎ 在Rt△PAC中，∠APC＝30°，‎ ‎∴AC＝(千米)．‎ 在△ACB中，∠CAB＝30°＋60°＝90°，‎ ‎∴BC＝＝＝(千米)，‎ 所求速度为：÷＝2(千米/时)．‎ ‎(2)∠DAC＝90°－60°＝30°，‎ sin∠DCA＝sin(180°－∠ACB)＝sin∠ACB＝＝＝，‎ sin∠CDA＝sin(∠ACB－30°)‎ ‎＝sin∠ACB·cos 30°－cos∠ACB·sin 30°‎ ‎＝×－× ‎＝，‎ 在△ACD中，由正弦定理得 ＝，‎ ‎∴AD＝＝＝(千米)，‎ 答：此时船距A岛千米．‎ ‎ ‎