2019届高考数学二轮复习 第6讲 空间线、面的平行与垂直关系学案（无答案）文 7页

第6讲 空间线、面的平行与垂直关系 学习目标 ‎【目标分解一】平行关系的判断与证明 ‎【目标分解二】垂直关系的判断与证明 ‎【目标分解三】探索性问题 重点 平行、垂直关系的证明， 垂直在全国Ⅰ卷中的考察尤为突出 难点 ‎ 性质定理的应用、探索性问题 ‎【课前自主复习区】‎ 一、熟记以下知识要点 ‎(1)线线平行的方法：①三角形的中位线等平面几何中的性质；②线面平行的性质定理；③面面平行的性质定理 ‎(2)线面平行的方法：①在平面内找一条直线与已知直线平行（直尺，你懂的），利用线面平行的判定定理；‎ ‎②寻找面面平行，利用面面平行的性质．‎ ‎(3)面面平行的方法：在一个平面内找两条相交的直线和另一个平面平行，利用面面平行的判定定理.‎ ‎(4)线线垂直的方法：异面垂直（高考中的意图） 利用线面垂直 共面垂直 利用平面几何的性质：等腰三线合一，菱形（正方形）对角线，勾股定理，直径所对圆周角是直角，三角形全等（相似），‎ 如果一个三角形一条边上的中线等于这条边的一半，那么这个三角形是直角三角形 ‎(5)线面垂直的方法：①在平面内找两条相交的直线与已知直线垂直，利用线面垂直的判定定理；‎ ‎②面面垂直的性质定理．‎ ‎(6)面面垂直的方法：在一个平面内找一条直线和另一个平面垂直，利用面面垂直的判定定理.‎ 二、规范作图、符号表示及证明步骤的严谨 范例： (2017·全国卷Ⅲ）19．如图，四面体ABCD中，△ABC是正三角形，AD=CD．‎ （1） 证明：AC⊥BD；‎ 7‎ ‎【课堂互动探究区】‎ ‎【目标分解一】平行关系的判断与证明 ‎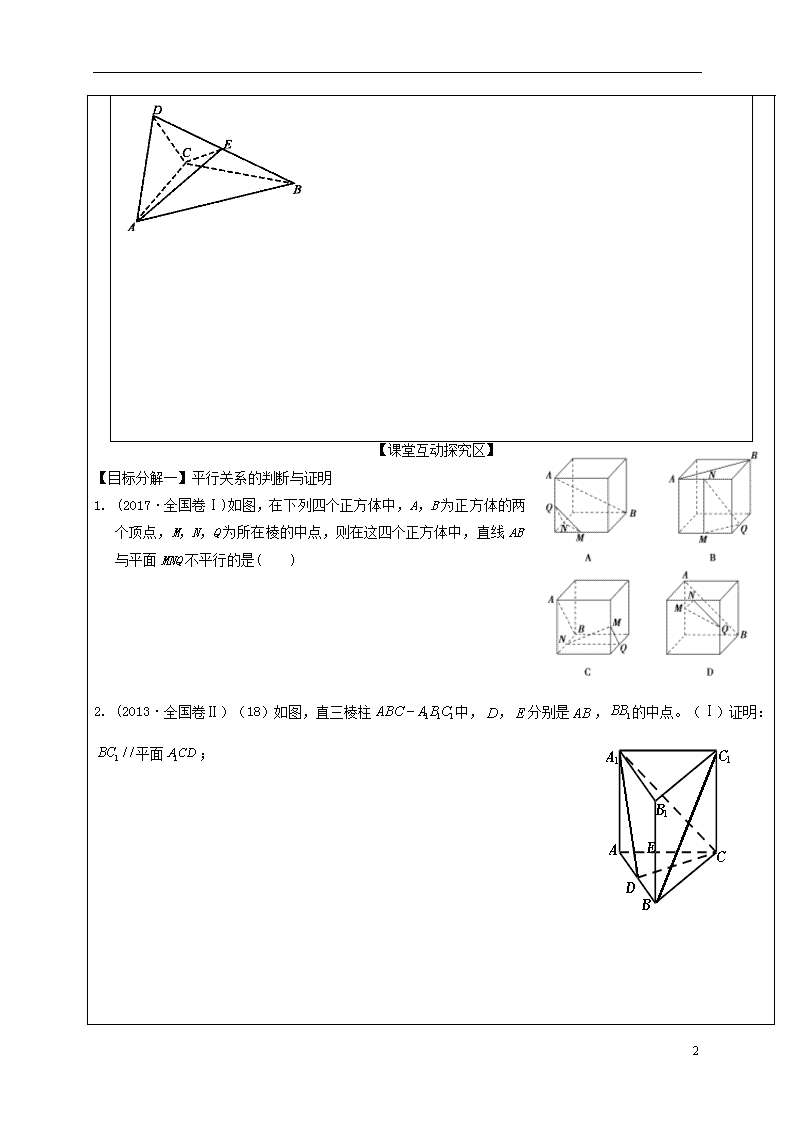1. (2017·全国卷Ⅰ)如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是(　　)‎ ‎2. (2013·全国卷Ⅱ）（18）如图，直三棱柱中，，分别是，的中点。（Ⅰ）证明：平面；‎ 7‎ ‎3. (2016·全国卷Ⅲ）（19）如图，四棱锥P-ABCD中，PA⊥地面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点. （I）证明MN∥平面PAB;‎ ‎★4.三棱柱,D是BC上一点，且，若是的中点，‎ 求证：平面 ‎【目标分解二】垂直关系的判断与证明 ‎1. (2013·全国卷Ⅰ）19 如图，三棱柱中，，，。（Ⅰ）证明：；‎ ‎2. (2015·全国卷Ⅰ）18 如图，四边形ABCD为菱形，G为AC与BD的交点，BE⊥平面ABCD.（Ⅰ）证明：平面AEC⊥平面BED 7‎ ‎3. 如图，在三棱锥中，分别为棱，，的中点．已知，，,.求证：（1）平面⊥平面．‎ ‎4. 如图，AB为圆O的直径，点E，F在圆O上，且AB∥EF，矩形ABCD所在的平面和圆O所在的平面互相垂直．‎ ‎(1)求证：平面AFC⊥平面CBF.‎ ‎★5. 如图，在矩形ABCD中， ，E，F分别为BC，DA的中点．将矩形ABCD沿线段EF折起，使得∠DFA＝60°.设G为AF的中点．(1)证明：AE⊥面BDG.‎ ‎6. (2016·全国卷Ⅰ）（18）如图，已知正三棱锥P-ABC的侧面是直角三角形，PA=6，顶点P在平面ABC内的正投影为点D，D在平面PAB内的正投影为点E，连结PE并延长交AB于点G.‎ ‎（I）证明：G是AB的中点；‎ ‎★（II）在图中作出点E在平面PAC内的正投影F（说明作法及理由）‎ 7‎ ‎★★7. (2017·全国卷Ⅲ）10．在正方体中，E为棱CD的中点，则 A． ‎ B． ‎ ‎ C． D．‎ ‎【目标分解三】探索性问题 方法 ①猜想证明（中点或1:2等分点等） ②直接求解 ‎★1. 如图，高为1的等腰梯形ABCD中，AM＝CD＝AB＝1，M为AB的三等分点，现将△AMD沿MD折起，使平面AMD⊥平面MBCD，连接AB，AC.‎ ‎(1)在AB边上是否存在点P，使AD∥平面MPC，请说明理由；‎ ‎★★2. 如图,直三棱柱中，侧棱长为2，，是的中点，上是否存在点，交于点,且，如果存在，求线段的长.‎ ‎ ‎ ‎【课后作业】：第96页 专题限时集训（十） A组 ★B组2、6、7题 7‎ ‎【解析】假设上是否存在点，设 则.‎ ‎ ‎ ‎【点评】（1）本题如果利用猜想证明法，猜想中点，但是本题恰好不是中点，所以显示出猜想证明法的局限性了. (2)本题利用的是直接探究法，直接通过解三角形（相似三角形）求得. 解三角形可以利用正弦定理、余弦定理、三角函数和相似三角形. ‎ ‎3．(2013·全国理卷Ⅱ)已知m，n为异面直线，m⊥平面α，n⊥平面β.直线l满足l⊥m，l⊥n，l⊄α，l⊄β，则(　　)‎ A．α∥β且l∥α B．α⊥β且l⊥β C．α与β相交，且交线垂直于l D．α与β相交，且交线平行于l ‎(2017·全国卷Ⅲ）10．在正方体中，E为棱CD的中点，则（ ）‎ A． B． C． D．‎ ‎(2014·全国卷Ⅱ）18 如图，四凌锥p—ABCD中，底面ABCD为矩形，PA上面ABCD，E为PD的点。 ‎ ‎（I）证明：PB//平面AEC;‎ ‎(2015·全国卷Ⅱ）19. 如图,长方体中AB=16,BC=10,‎ 7‎ ‎,点E,F分别在上,过点E,F的平面与此长方体的面相交,交线围成一个正方形.‎ ‎（I）在图中画出这个正方形（不必说明画法与理由）；‎ ‎(2014·全国卷Ⅰ）19 如图，三棱柱中，侧面为菱形，的中点为，且平面.‎ ‎（I）证明：‎ ‎(2017·全国卷Ⅰ）18．如图，在四棱锥P-ABCD中，AB//CD，且．‎ （1） 证明：平面PAB⊥平面PAD；‎ ‎ (2016·全国卷Ⅱ)如图103，菱形ABCD的对角线AC与BD交于点O，点E，F分别在AD，CD上，AE＝CF，EF交BD于点H.将△DEF沿EF折到△D′EF的位置．‎ ‎(1)证明：AC⊥HD′；‎ ‎【课后作业】：‎ 7‎