- 659.00 KB
- 2021-05-14 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
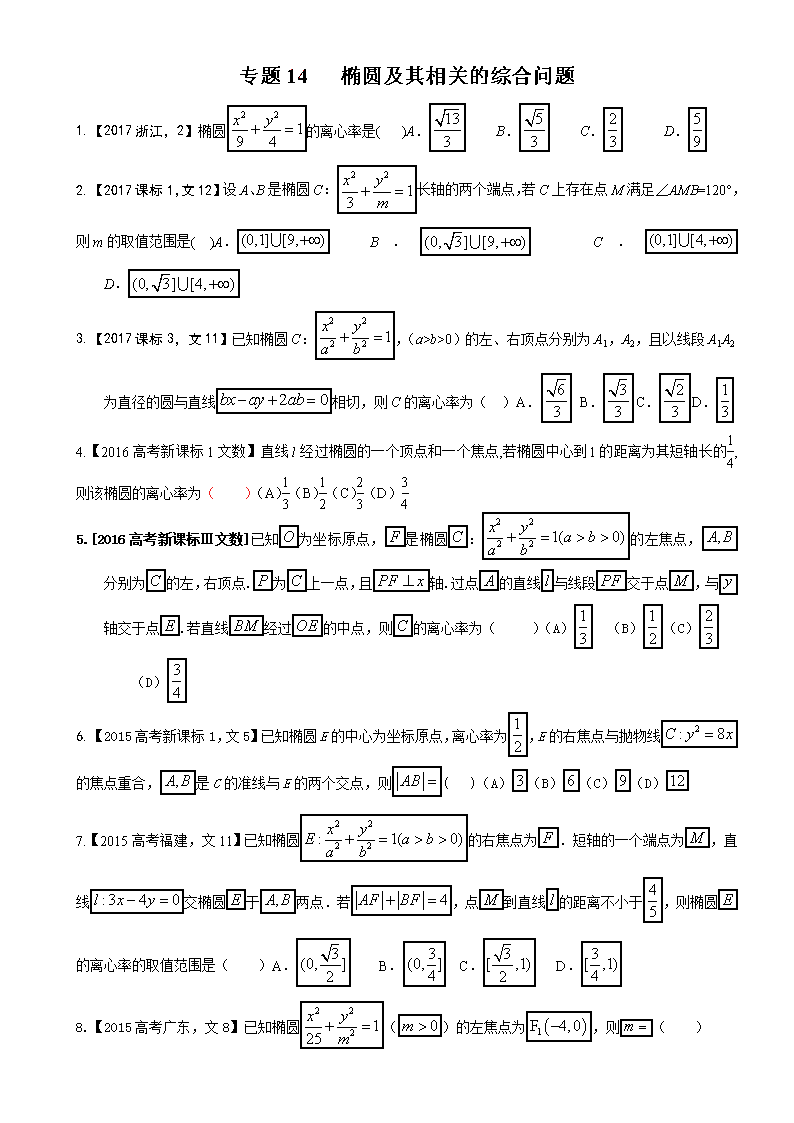
专题14 椭圆及其相关的综合问题
1.【2017浙江,2】椭圆的离心率是( )A. B. C. D.
2.【2017课标1,文12】设A、B是椭圆C:长轴的两个端点,若C上存在点M满足∠AMB=120°,则m的取值范围是( )A. B. C. D.
3.【2017课标3,文11】已知椭圆C:,(a>b>0)的左、右顶点分别为A1,A2,且以线段A1A2为直径的圆与直线相切,则C的离心率为( )A. B. C. D.
4.【2016高考新课标1文数】直线l经过椭圆的一个顶点和一个焦点,若椭圆中心到l的距离为其短轴长的,则该椭圆的离心率为( )(A)(B)(C)(D)
5.[2016高考新课标Ⅲ文数]已知为坐标原点,是椭圆:的左焦点,分别为的左,右顶点.为上一点,且轴.过点的直线与线段交于点,与轴交于点.若直线经过的中点,则的离心率为( )(A) (B) (C) (D)
6.【2015高考新课标1,文5】已知椭圆E的中心为坐标原点,离心率为,E的右焦点与抛物线的焦点重合,是C的准线与E的两个交点,则( )(A)(B)(C)(D)
7.【2015高考福建,文11】已知椭圆的右焦点为.短轴的一个端点为,直线交椭圆于两点.若,点到直线的距离不小于,则椭圆的离心率的取值范围是( )A. B. C. D.
8.【2015高考广东,文8】已知椭圆()的左焦点为,则( )
A.B.C.D.
9.【2015高考浙江,文15】椭圆()的右焦点关于直线的对称点在椭圆上,则椭圆的离心率是________.
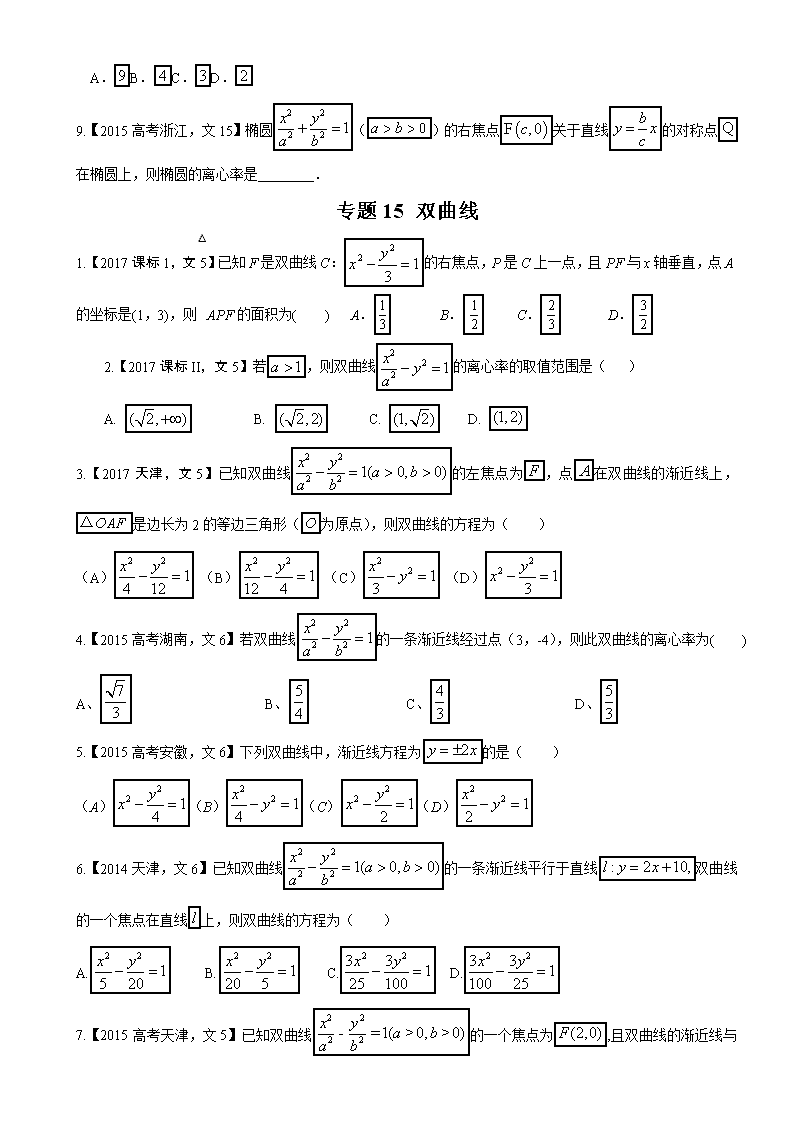
专题15 双曲线
1.【2017课标1,文5】已知F是双曲线C:的右焦点,P是C上一点,且PF与x轴垂直,点A的坐标是(1,3),则△APF的面积为( ) A. B. C. D.
2.【2017课标II,文5】若,则双曲线的离心率的取值范围是( )
A. B. C. D.
3.【2017天津,文5】已知双曲线的左焦点为,点在双曲线的渐近线上,是边长为2的等边三角形(为原点),则双曲线的方程为( )
(A) (B) (C) (D)
4.【2015高考湖南,文6】若双曲线的一条渐近线经过点(3,-4),则此双曲线的离心率为( )
A、 B、 C、 D、
5.【2015高考安徽,文6】下列双曲线中,渐近线方程为的是( )
(A)(B)(C)(D)
6.【2014天津,文6】已知双曲线的一条渐近线平行于直线双曲线的一个焦点在直线上,则双曲线的方程为( )
A. B. C. D.
7.【2015高考天津,文5】已知双曲线的一个焦点为
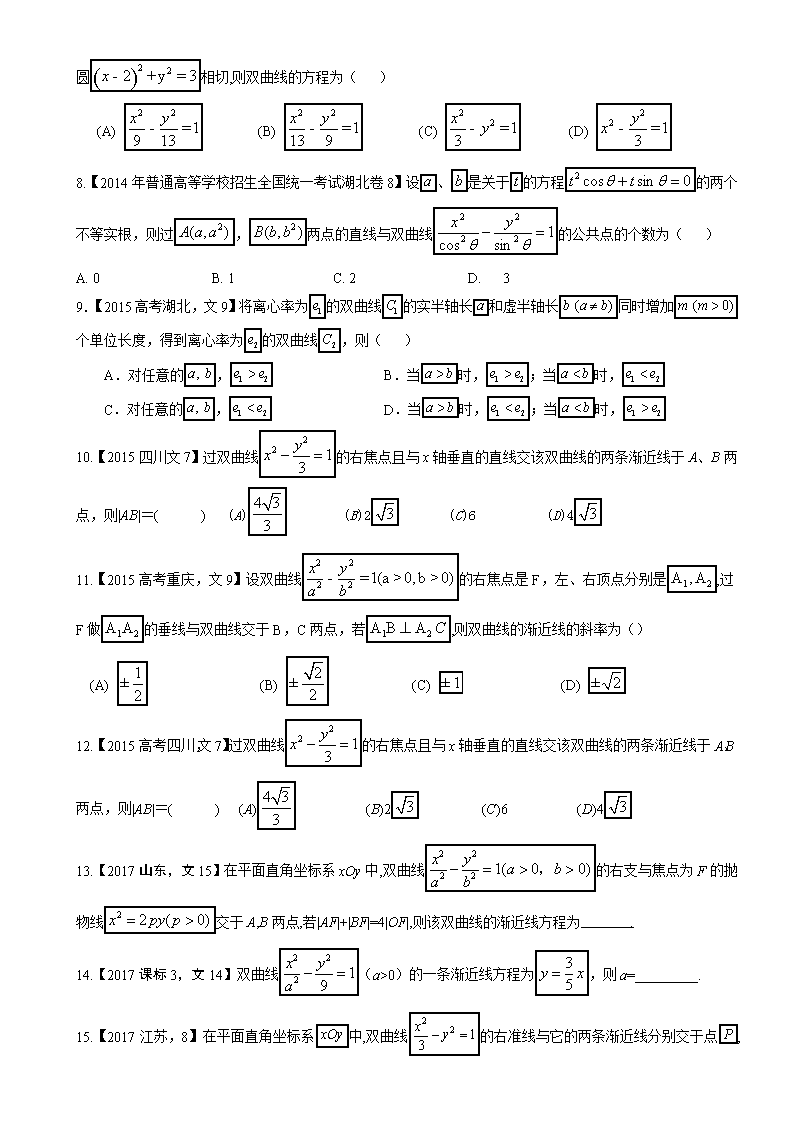
,且双曲线的渐近线与圆相切,则双曲线的方程为( )
(A) (B) (C) (D)
8.【2014年普通高等学校招生全国统一考试湖北卷8】设、是关于的方程的两个不等实根,则过,两点的直线与双曲线的公共点的个数为( )
A. 0 B. 1 C. 2 D. 3
9.【2015高考湖北,文9】将离心率为的双曲线的实半轴长和虚半轴长同时增加个单位长度,得到离心率为的双曲线,则( )
A.对任意的, B.当时,;当时,
C.对任意的, D.当时,;当时,
10.【2015四川文7】过双曲线的右焦点且与x轴垂直的直线交该双曲线的两条渐近线于A、B两点,则|AB|=( ) (A) (B)2 (C)6 (D)4
11.【2015高考重庆,文9】设双曲线的右焦点是F,左、右顶点分别是,过F做的垂线与双曲线交于B,C两点,若,则双曲线的渐近线的斜率为()
(A) (B) (C) (D)
12.【2015高考四川,文7】过双曲线的右焦点且与x轴垂直的直线交该双曲线的两条渐近线于A、B两点,则|AB|=( )[来源:Zxxk.Com](A) (B)2 (C)6 (D)4
13.【2017山东,文15】在平面直角坐标系xOy中,双曲线的右支与焦点为F的抛物线交于A,B两点,若|AF|+|BF|=4|OF|,则该双曲线的渐近线方程为 .[来源:Z&xx&k.Com]
14.【2017课标3,文14】双曲线(a>0)的一条渐近线方程为,则a=_________.
15.【2017江苏,8】在平面直角坐标系中,双曲线的右准线与它的两条渐近线分别交于点,
,其焦点是,则四边形的面积是________.
专题16 抛物线
1.2017课标II,文12】过抛物线的焦点,且斜率为的直线交于点(在轴上方),为的准线,点在上且,则到直线的距离为( )
A. B. C. D.
2.【2014,安徽文3】抛物线的准线方程是()A. B. C. D.
3.【2014全国1,文10】已知抛物线的焦点为,是上一点,,则( )
A. 1 B. 2 C. 4 D. 8
4.【2014辽宁文8】已知点在抛物线C:的准线上,记C的焦点为F,则直线AF的斜率为( )A. B. C. D.
5.【2014四川,文10】已知是抛物线的焦点,点,在该抛物线上且位于轴的两侧,(其中为坐标原点),则与面积之和的最小值是()
A. B. C. D.
6.【2015高考陕西,文3】已知抛物线的准线经过点,则抛物线焦点坐标为()
A.B.C.D.
7.【2016高考四川文科】抛物线的焦点坐标是( ) (A)(0,2) (B) (0,1) (C) (2,0) (D) (1,0)
8.【2014全国2,文10】设为抛物线的焦点,过且倾斜角为的直线交于,两点,则( ) (A)(B)(C)(D)
9.【2016高考新课标2文数】设F为抛物线C:y2=4x的焦点,曲线y=(k>0)与C交于点P,PF⊥x轴,则k=()
(A)(B)1 (C)(D)2
10.【2017天津,文12】设抛物线的焦点为F,准线为l.已知点C在l上,以C为圆心的圆与y轴的正半轴相切于点A.若,则圆的方程为 .
11.【2014上海,文4】若抛物线y2=2px的焦点与椭圆的右焦点重合,则该抛物线的准线方程为___________.
12.【2014高考陕西版文第11题】抛物线的准线方程为________.