高考数学抛物线焦点弦的性质 2页

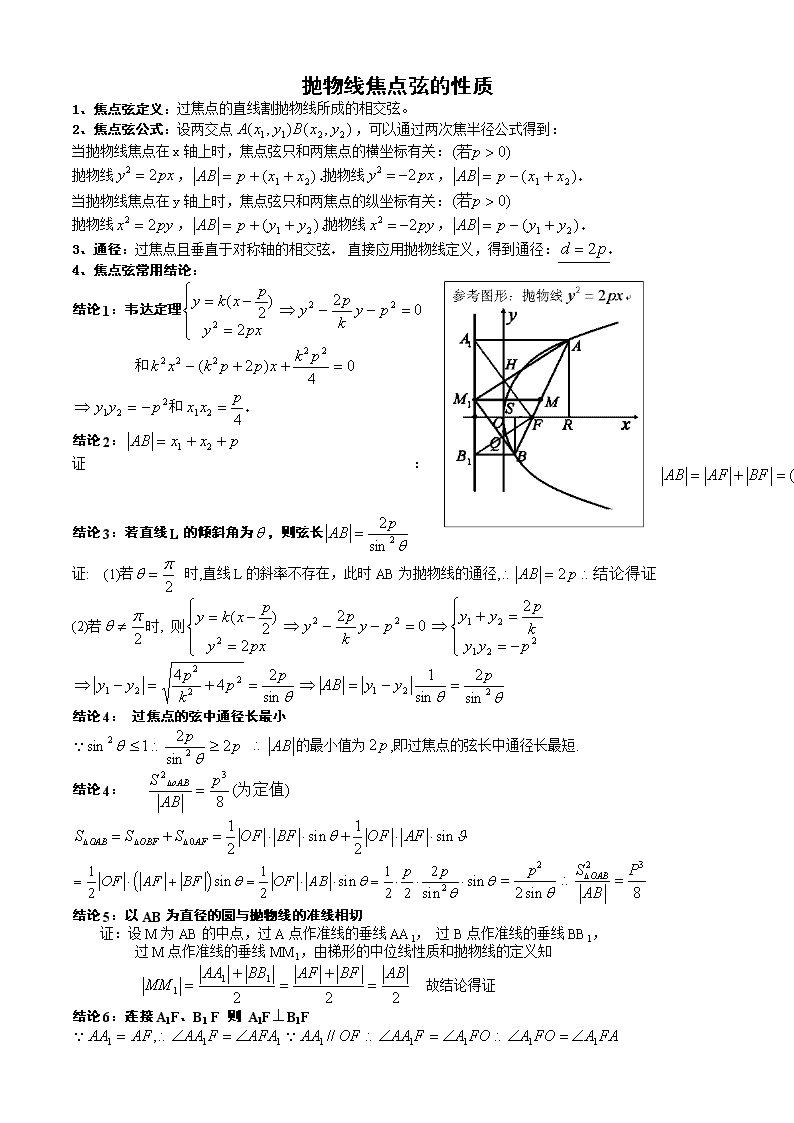
抛物线焦点弦的性质 ‎1、焦点弦定义：过焦点的直线割抛物线所成的相交弦。‎ ‎2、焦点弦公式：设两交点，可以通过两次焦半径公式得到：‎ 当抛物线焦点在x轴上时，焦点弦只和两焦点的横坐标有关：‎ 抛物线，抛物线，‎ 当抛物线焦点在y轴上时，焦点弦只和两焦点的纵坐标有关：‎ 抛物线，抛物线，‎ ‎3、通径：过焦点且垂直于对称轴的相交弦 直接应用抛物线定义，得到通径：‎ ‎4、焦点弦常用结论：‎ 结论1：韦达定理 和 和 结论2：‎ 证：‎ 结论3：若直线L的倾斜角为，则弦长 证: (1)若 时,直线L的斜率不存在，此时AB为抛物线的通径,‎ ‎(2)若时, 则 结论4： 过焦点的弦中通径长最小 ‎ 的最小值为,即过焦点的弦长中通径长最短.‎ 结论4： ‎ 结论5：以AB为直径的圆与抛物线的准线相切 ‎ ‎ 证：设M为AB的中点，过A点作准线的垂线AA1， 过B点作准线的垂线BB1， ‎ ‎ 过M点作准线的垂线MM1，由梯形的中位线性质和抛物线的定义知 ‎ 故结论得证 ‎ 结论6：连接A‎1F、B‎1 F 则 A‎1FB‎1F ‎ 同理 A‎1FB‎1 F 结论7：（1）AM1BM1 （2）M‎1FAB （3）‎ ‎（4）设AM1 与A‎1F相交于H ，M1B与 FB1相交于Q 则M1，Q，F ，H四点共圆 ‎（5）‎ 证：由结论（6）知M1 在以AB为直径的圆上 AM1BM1 ‎ 为直角三角形， M1 是斜边A1 B1 的中点 ‎ ‎ M‎1FAB ‎ AM1BM1 ‎ ‎ 所以M1，Q，F,H四点共圆，‎ ‎ ‎ 结论8： （1）O、B1 三点共线 （2）B，O，A1 三点共线 ‎ （3）设直线AO与抛物线的准线的交点为B1，则BB1平行于X轴 ‎（4）设直线BO与抛物线的准线的交点为A1，则AA1平行于X轴 证：因为，而 所以所以三点共线。同理可征（2）（3）（4）‎ 结论9： ‎ 证：过A点作AR垂直X轴于点R，过B点作BS垂直X轴于点S，设准线与轴交点为E,‎ 则 ‎ 同理可得 ‎