【物理】2020届一轮复习人教版曲线运动运动的合成与分解课时作业 6页

2020 届一轮复习人教版 曲线运动运动的合成与分解 课时作业 A 组 1．关于运动的合成，下列说法中错误的是(B) A．两个分运动的时间一定与它们的合运动的时间相等 B．合运动的速度一定比每一个分运动的速度大 C．曲线运动一定是变速运动 D．做曲线运动的物体，所受合力一定不为零 【解析】两个分运动的时间一定与它们的合运动的时间相等，选项 A 正确；合运动的速度可以比每一 个分运动的速度大，也可以小，也可以相等，选项 B 错误；曲线运动的速度的方向不断变化，故一定是变 速运动，选项 C 正确；做曲线运动的物体加速度一定不为零，所受合力一定不为零，选项 D 正确；此题选 错误的选项，故选 B. 2．(多选)下列对曲线运动的理解正确的是(CD) A．物体做曲线运动时，加速度一定变化 B．做曲线运动的物体不可能受恒力作用 C．曲线运动可以是匀变速曲线运动 D．做曲线运动的物体，速度的大小可以不变 【解析】物体做曲线运动的条件是合力与速度不在同一条直线上，加速度大小和方向不一定变化，如 平抛运动，故 A 错误，C 正确，B 错误；做曲线运动的物体，速度大小可以不变，如匀速圆周运动，故 D 正确． 3．质量为 1 kg 的物体在水平面内做曲线运动，已知互相垂直方向上的速度图象分别如图所示．下列 说法正确的是(D) A．物体的初速度为 5 m/s B．物体所受的合外力为 3 N C．2 s 末物体速度大小为 7 m/s D．物体初速度的方向与合外力方向垂直 【解析】由图象知，物体在 y 方向以 4 m/s 做匀速直线运动．在 x 方向以加速度 1.5 m/s2 做初速为 0 的匀加速直线运动，物体的初速度为 4 m/s，A 错．物体所受合外力大小为 1.5 N．方向与初速度方向垂直， B 错，D 对.2 s 末，vx＝1.5×2 m/s＝3 m/s.∴v2＝ v2 x＋v2 y，v2＝5 m/s，C 错． 4．如图所示，一轻绳通过无摩擦的定滑轮 O 与小球 B 连接，另一端与套在光滑竖直杆上的小物块 A 连接，杆两端固定且足够长，物块 A 由静止从图示位置释放后，先沿杆向上运动．设某时刻物块 A 运动的 速度大小为 vA，小球 B 运动的速度大小为 vB，轻绳与杆的夹角为θ.则(B) A．vA＝vBcos θ B．vB＝vAcos θ C．A 物体上升过程中绳中张力不变 D．A 上升过程中，绳中张力始终小于 B 的重力 【解析】把 A 的速度沿垂直于绳的方向和沿着绳的方向分解如图示，可得：vB＝vAcos θ.A 错，B 对．当 A 上升到与 O 点等高时，B 的速度为 0.B 先做加速运动后做减速运动．绳中张力先小于 B 的重力，后大于 B 的重力，C、D 均错． 5．小船过河时，船头与上游河岸夹角为α，其航线恰好垂直于河岸，已知船在静水中的速度为 v，现 水流速度稍有增大，为保持航线不变，且能准时到达河对岸，下列措施中可行的是(B) A．减小α角，减小船速 v B．减小α角，增大船速 v C．增大α角，增大船速 v D．增大α角，减小船速 v 【解析】“稍有增大”说明水流速度变化不大，“准时到达”说明合速度大小不变．据此依平行四边 形定则作出速度合成图如下，可知，B 对． 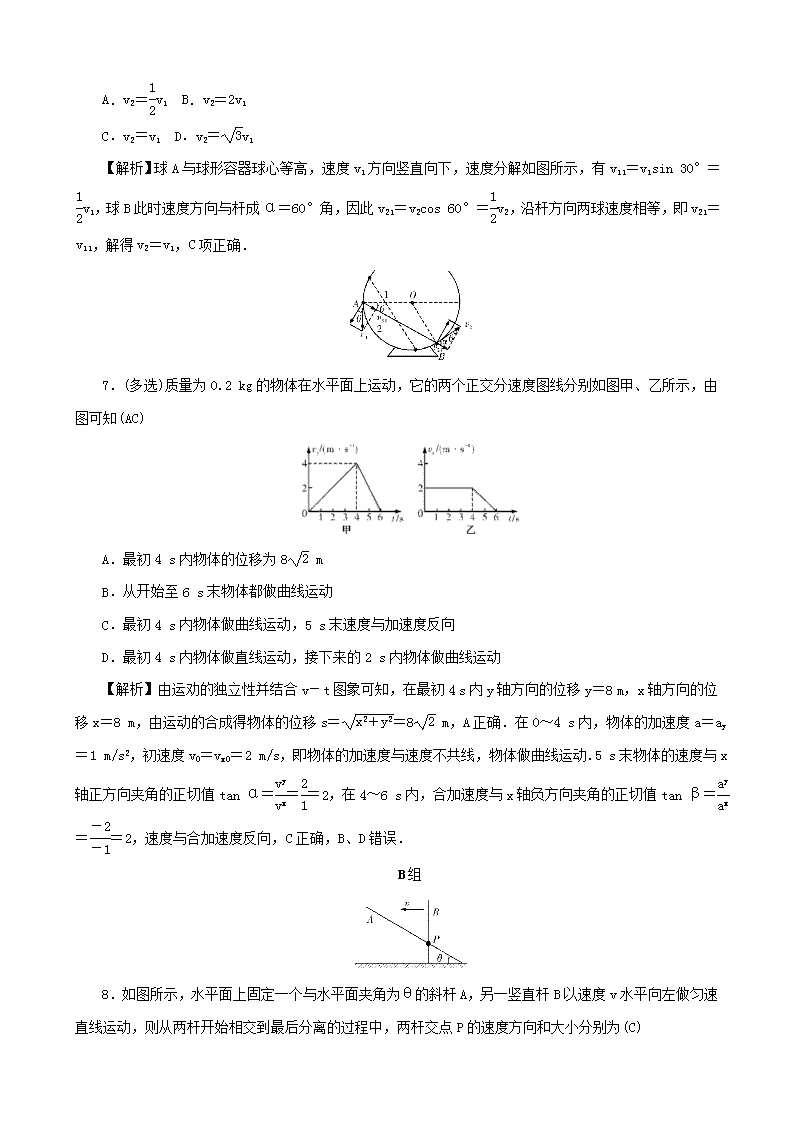6．一轻杆两端分别固定质量为 mA 和 mB 的两个小球 A 和 B(可视为质点)．将其放在一个光滑球形容器 中，从位置 1 开始下滑，如图所示，当轻杆到达位置 2 时球 A 与球形容器球心等高，其速度大小为 v1，已 知此时轻杆与水平方向成θ＝30°角，B 球的速度大小为 v2，则(C) A．v2＝1 2 v1 B．v2＝2v1 C．v2＝v1 D．v2＝ 3v1 【解析】球 A 与球形容器球心等高，速度 v1 方向竖直向下，速度分解如图所示，有 v11＝v1sin 30°＝ 1 2 v1，球 B 此时速度方向与杆成α＝60°角，因此 v21＝v2cos 60°＝1 2 v2，沿杆方向两球速度相等，即 v21＝ v11，解得 v2＝v1，C 项正确． 7．(多选)质量为 0.2 kg 的物体在水平面上运动，它的两个正交分速度图线分别如图甲、乙所示，由 图可知(AC) A．最初 4 s 内物体的位移为 8 2 m B．从开始至 6 s 末物体都做曲线运动 C．最初 4 s 内物体做曲线运动，5 s 末速度与加速度反向 D．最初 4 s 内物体做直线运动，接下来的 2 s 内物体做曲线运动 【解析】由运劝的独立性并结合 v－t 图象可知，在最初 4 s 内 y 轴方向的位移 y＝8 m，x 轴方向的 位移 x＝8 m，由运动的合成得物体的位移 s＝ x2＋y2＝8 2 m，A 正确．在 0～4 s 内，物体的加速度 a＝ ay＝1 m/s2，初速度 v0＝vx0＝2 m/s，即物体的加速度与速度不共线，物体做曲线运动.5 s 末物体的速度与 x 轴正方向夹角的正切值 tan α＝vy vx ＝2 1 ＝2，在 4～6 s 内，合加速度与 x 轴负方向夹角的正切值 tan β ＝ay ax ＝－2 －1 ＝2，速度与合加速度反向，C 正确，B、D 错误． B 组 8．如图所示，水平面上固定一个与水平面夹角为θ的斜杆 A，另一竖直杆 B 以速度 v 水平向左做匀速 直线运动，则从两杆开始相交到最后分离的过程中，两杆交点 P 的速度方向和大小分别为(C) A．水平向左，大小为 v B．竖直向上，大小为 vtan θ C．沿 A 杆斜向上，大小为 v cos θ D．沿 A 杆斜向上，大小为 vcos θ 【解析】两杆的交点 P 参与了两个分运动：与 B 杆一起以速度 v 水平向左的匀速直线运动和沿 B 杆竖 直向上的匀速运动，交点 P 的实际运动方向沿 A 杆斜向上，如图所示，则交点 P 的速度大小为 vP＝ v cos θ ， 故 C 正确． 9．在一光滑的水平面上建立 xOy 平面坐标系，一质点在水平面上从坐标原点开始运动，沿 x 方向和 y 方向的 x－t 图象和 vy－t 图象分别如图甲、乙所示，求： (1)运动后 4 s 内质点的最大速度； (2)4 s 末质点离坐标原点的距离． 【解析】(1)由题图可知，质点沿 x 轴正方向做匀速直线运动，速度大小为 vx＝x t1 ＝2 m/s，在运动后 4 s 内，沿 y 轴方向运动的最大速度为 4 m/s，则运动后 4 s 内质点运动的最大速度有 vm＝ v2 x＋v2 y＝2 5 m/s. (2)0～2 s 内质点沿 y 轴正方向做匀加速直线运动，2～4 s 内先沿 y 轴正方向做匀减速直线运动，再 沿 y 轴负方向做初速度为零的匀加速直线运动，此时加速度大小为 a＝Δv Δt ＝6 2 m/s2＝3 m/s2 则质点沿 y 轴正方向做匀减速运动的时间 t2＝v a ＝2 3 s 则运动后的 4 s 内沿 y 轴方向的位移 y＝1 2 ×2×(2＋2 3 ) m－1 2 ×4×4 3 m＝0 因此 4 s 末质点离坐标原点的距离等于沿 x 轴方向的位移 由题图甲可知，4 s 末质点离坐标原点的距离 s＝x＝8 m 10．一小船渡河，河宽 d＝180 m，水流速度 v1＝2.5 m/s. (1)若船在静水中的速度为 v2＝5 m/s，欲使船在最短的时间内渡河，船头应朝什么方向？用多长时间？ 位移是多少？ (2)若船在静水中的速度为 v2＝5 m/s，欲使船渡河的航程最短，船头应朝什么方向？用多长时间？位 移是多少？ (3)若船在静水中的速度为 v2＝1.5 m/s，欲使船渡河的航程最短，船头应朝什么方向？用多长时间？ 位移是多少？ 【解析】将船实际的速度(合速度)分解为垂直于河岸方向和平行于河岸方向的两个分速度，垂直于河 岸的分速度影响渡河的时间，而平行于河岸的分速度只影响船在平行于河岸方向的位移． (1)若 v2＝5 m/s，欲使船在最短的时间内渡河，船头应垂直于河岸方向，如图所示，合速度为倾斜方 向，垂直于河岸的分速度为 v2＝5 m/s. t＝ d v⊥ ＝d v2 ＝180 5 s＝36 s v 合＝ v2 1＋v2 2＝5 2 5 m/s x＝v 合 t＝90 5 m (2)若 v2＝5 m/s，欲使船渡河的航程最短，合速度应沿垂直于河岸方向，船头应朝图中的 v2 方向．垂 直于河岸过河，则要求 v∥＝0，有 v2sin θ＝v1，得θ＝30°，所以当船头与上游河岸成 60°角时航程最 短． x＝d＝180 m t＝ d v⊥ ＝ d v2cos 30° ＝ 180 5 2 3 s＝24 3 s. (3)若 v2＝1.5 m/s，与(2)中不同，因为船速小于水速，所以船一定向下游漂移，设合速度方向与河 岸下游方向夹角为α，欲使航程最短，需α最大，如图所示，由出发点 A 作出 v1 矢量，以 v1 矢量末端为圆 心，v2 大小为半径作圆，A 点与圆周上某点的连线为合速度方向，欲使 v 合与河岸下游方向的夹角最大，应 使 v 合与圆相切，即 v 合⊥v2. 由 sin α＝v2 v1 ＝3 5 ，得α＝37° 所以船头应朝与上游河岸成 53°角方向． t＝ d v2cos α ＝180 1.2 s＝150 s v 合＝v1cos α＝2 m/s x＝v 合 t＝300 m.