2019届二轮复习机械能守恒定律及能量守恒定律的综合应用课件（共38张） 38页

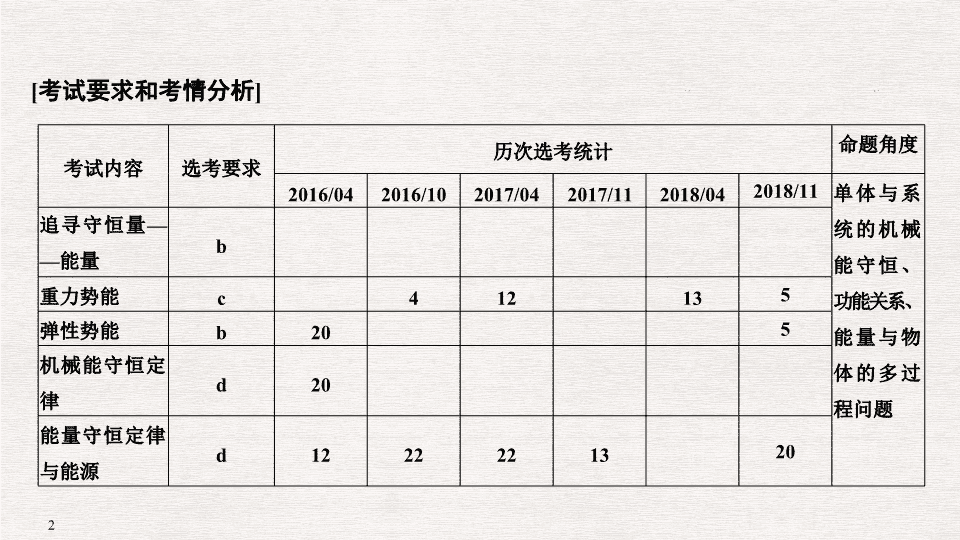
第 9 讲 机械能守恒定律及能量守恒定律的综合应用 [ 考试要求和考情分析 ] 考试内容 选考要求 历次选考统计 命题角度 2016/04 2016/10 2017/04 2017/11 2018/04 2018/11 单体与系统的机械能守恒、功能关系、能量与物体的多过程问题 追寻守恒量 —— 能量 b           重力势能 c   4 12   13 5 弹性势能 b 20         5 机械能守恒定律 d 20         能量守恒定律与能源 d 12 22 22 13   20 对重力势能、弹性势能的理解 [ 要点总结 ] 1. 对重力做功和重力势能的提醒 ( 1) 重力做功的大小与物体的运动状态无关，与物体是否受其他力无关； ( 2) 重力做功，一定会引起重力势能的变化； ( 3) 重力势能是标量，但有正负，其意义表示物体的重力势能比它在参考平面的重力势能大还是小 。 2. 重力势能的求解方法 ( 1) 定义法：选取参考平面，确定物体相对参考平面的高度 h ，代入 E p ＝ mgh 求解重力势能。 ( 2) W G 和 E p 关系法：由 W G ＝ E p1 － E p2 知 E p2 ＝ E p1 － W G 或 E p1 ＝ W G ＋ E p2 。 [ 精典题组 ] 1. ( 2018· 浙江金华十校联考 ) 如图 1 所示，巴西奥运会上，中国选手邓薇以 262 公斤 ( 抓举 115 公斤，挺举 147 公斤 ) 的总成绩打破奥运会纪录、世界纪录。某次抓举，在杠铃被举高的整个过程中，不计空气阻力，下列说法正确的是 ( 　　 ) 图 1 A. 杠铃的动能一直增大 B. 杠铃的重力势能一直增大 C. 杠铃的机械能守恒 D. 杠铃一直处于超重 状态 解析　 杠铃被举高的过程一定经历了先加速向上，后减速向上的运动，所以动能应先增大后减小，选项 A 错误；杠铃一直向上运动，重力势能一直增大，选项 B 正确；因人对杠铃的支持力做正功，杠铃的机械能增加，选项 C 错误；加速度先向上，后向下，杠铃先超重，后失重，选项 D 错误。 答案　 B 2. 如图 2 所示，物块 A 质量为 m ，置于水平地面上。一根轻质弹簧，原长为 L ，劲度系数为 k ，下端与物块 A 相连接。现将弹簧上端点 P 缓慢地竖直提起一段高度 h 使物块 A 离开地面。这时重物具有的重力势能为 ( 以地面为零势能面 )( 　　 ) 图 2 答案 　 A 机械能守恒定律及其应用 [ 要点总结 ] 1. 机械能守恒的判定方法 ( 1) 做功判断法：若物体系统内只有重力或弹簧弹力做功，其他力均不做功或其他力做功的代数和为零，则系统的机械能守恒。 ( 2) 能量转化判断法：若只有系统内物体间动能和重力势能及弹性势能的相互转化，系统跟外界没有发生机械能的传递，机械能也没有转变成其他形式的能 ( 如没有内能增加 ) ，则系统的机械能守恒 。 2. 机械能守恒定律的 表达式 图 3 答案 　 A [ 精典题组 ] 3. ( 2018· 浙江嘉兴一模 ) 如图 4 是一种名为 “ 牙签弩 ” 的玩具弓弩，现竖直向上发射木质牙签， O 点为皮筋自然长度位置， A 为发射的起点位置。若不计一切阻力，则 ( 　　 ) 图 4 A. A 到 O 的过程中，牙签一直处于超重状态 B. A 到 O 的过程中，牙签的机械能守恒 C. 在上升过程中，弓和皮筋的弹性势能转化为牙签的动能 D. 根据牙签向上飞行的高度可测算出牙签被射出时的 速度 解析 　从 A 到 O 的过程中，牙签受重力和弹力，当弹力大于重力时是加速上升，处于超重状态；当弹力小于重力时，减速上升，是失重状态，选项 A 错误； A 到 O 的过程中，牙签的动能和势能均增加，故机械能增加，选项 B 错误；在上升过程中，系统机械能守恒，弓和皮筋的弹性势能逐渐转化为牙签的动能和重力势能，选项 C 错误；由于不计一切阻力，牙签向上飞行过程是竖直上抛运动，根据运动学公式 v 2 ＝ 2 gh 可知，根据牙签向上飞行的高度可测算出牙签被射出时的速度，选项 D 正确。 答案 　 D 4. ( 2018· 浙江瑞安选考模拟 ) 总质量约为 3.8 吨 “ 嫦娥三号 ” 探测器在距月面 3 m 处关闭反推发动机，让其以自由落体方式降落在月球表面。 4 条着陆腿触月信号显示， “ 嫦娥三号 ” 完美着陆月球虹湾地区。月球表面附近重力加速度约为 1.6 m/s 2 ， 4 条着陆腿可视作完全相同的四个轻弹簧，在软着陆后，每个轻弹簧获得的弹性势能大约是 ( 　　 ) 图 5 A.28 500 J B.4 560 J C.18 240 J D.9 120 J 答案　 B 5. ( 2018· 浙江宁波适应性考试 ) 宁波高中科技新苗项目的同学在一个连锁机关游戏中，设计了一个如图 6 所示的起始触发装置： AB 段是长度连续可调的竖直伸缩杆， BCD 段是半径为 R 的四分之三圆弧弯杆， DE 段是长度为 2 R 的水平杆，与 AB 杆稍稍错开。竖直杆外套有下端固定且劲度系数较大的轻质弹簧，在弹簧上端放置质量为 m 的套环。每次将弹簧的长度压缩至 P 点后锁定，设 PB 的高度差为 h ，解除锁定后弹簧可将套环弹出，在触发器的右侧有多米诺骨牌，多米诺骨牌的左侧最高点 Q 和 P 点等高，且与 E 的水平距离为 x ( 可以调节 ) ，已知弹簧锁定时的弹性势能 E p ＝ 10 mgR ，套环 P 与水平杆 DE 段的动摩擦因数 μ ＝ 0.5 ，与其他部分的摩擦可以忽略不计，不计套环受到的空气阻力及解除锁定时的弹性势能损失，不考虑伸缩竖直杆粗细变化对套环的影响，重力加速度为 g 。求 ： 图 6 (1) 当 h ＝ 7 R 时，套环到达杆的最高点 C 处时的速度大小； (2) 在 (1) 问中套环运动到最高点 C 时对杆作用力的大小和方向； (3) 若 h 在 3 R 至 10 R 连续可调，要使该套环恰能击中 Q 点，则 x 应该在哪个范围内调节 ？ 解得 F C ＝ 3 mg ，由牛顿第三定律，套环对杆的作用力为 3 mg ，方向向上。 (3) 套环恰能击中 Q 点，环由 E 到 Q 做平抛 运动 x ＝ v E t 从 P 到 E ，根据能量守恒定律 有 6. ( 2018· 浙江诸暨选考模拟 ) 如图 7 所示，两个半径为 R 的四分之一圆弧构成的光滑细管道 ABC 竖直放置，且固定在光滑水平面上，圆心连线 O 1 O 2 水平。轻弹簧左端固定在竖直挡板上，右端与质量为 m 的小球接触 ( 不拴接，小球的直径略小于管的内径 ) ，长为 R 的薄板 DE 置于水平面上，板的左端 D 到管道右端 C 的水平距离为 R 。开始时弹簧处于锁定状态，具有的弹性势能为 3 mgR ，其中 g 为重力加速度。解除锁定，小球离开弹簧后进入管道，最后从 C 点抛出 。 图 7 (1) 求小球经 C 点时的动能； (2) 求小球经 C 点时所受的弹力； (3) 弹簧锁定时弹簧的弹性势能 E p 满足什么条件，从 C 点抛出的小球才能击中薄板 DE? 解析　 (1) 解除锁定后，小球运动到 C 点的过程，弹簧和小球组成的系统机械能守恒 由机械能守恒定律得 3 mgR ＝ 2 mgR ＋ E k 解得 E k ＝ mgR 。 设小球经过 C 点时轨道对小球的作用力为 F 由牛顿第二定律 得 若要小球击中薄板，应满足 R ≤ x 1 ≤ 2 R 功能关系、能量守恒定律与能源 [ 要点总结 ] 1. 功能关系的应用技巧 运用 功能关系解题时，应弄清楚重力或弹力做什么功，合外力做什么功，除重力、弹力外的力做什么功，从而判断重力势能或弹性势能、动能、机械能的变化。 2. 运用能量守恒定律解题的基本思路 ( 1) 确定初、末态。 ( 2) 分析状态变化过程中哪种形式的能量减少，哪种形式的能量增加。 ( 3) 能量的减少量与能量的增加量一定相等，即 Δ E 减 ＝ Δ E 增 。 [ 典例分析 ] 【例 2 】 (2018· 浙江台州高三期末 ) 如图 8 所示为一自由式滑雪空中技巧比赛场地示意图，比赛场地由出发区 AB 、助滑坡 BC 、第一过渡区 CD 、跳台 DE 、第二过渡区 EF 、着陆坡 FG 和终点区 GH 组成，在 H 处安置半径为 R ＝ 2.0 m 的圆形轨道，出口靠近但相互错开。第一过渡区和终点区的最低点在同一水平地面上，出发区距地面的高度 h B ＝ 8.4 m ，跳台最高点 E 和着陆坡最高点 F 离地面的高度均为 h 0 ＝ 4.0 m ，着陆坡坡度为 37° 。运动员从助滑坡顶端 B 由静止滑下，离开跳台在空中完成预定动作后到达 F 点正上方以水平速度 v ＝ 4.0 m/s 飞出，在落到倾斜雪道 FG 上时，运动员靠改变姿势进行缓冲使自己只保留沿斜面方向的分速度而不弹起。假设运动员连同滑雪板的总质量 m ＝ 100 kg ，除缓冲外运动员可视为质点，滑雪板与雪道 GH 间的动摩擦因数 μ ＝ 0.2 ，不计其余滑道和空气的阻力， sin 37° ＝ 0.6 ， cos 37° ＝ 0.8 ，取 g ＝ 10 m/s 2 ，求 ： 图 8 (1) 运动员到达 F 点正上方时离地面的高度 h ； (2) 运动员在倾斜雪道 FG 上滑行的距离； (3) 若运动员能够不脱离圆形轨道顺利通过最高点，雪道 GH 的最大长度 。 解析 　 (1) 运动员连同滑雪板从 B 点运动到 F 点正上方过程， (2) 设运动员落在倾斜雪道 K 点，离地高度为 h 1 代入数据后解得 h 1 ＝ 0.4 m 或 5.8 m ( 不合题意 ) (3) 运动员落在倾斜雪道 K 点保留沿斜面方向的速度 v K ＝ v cos 37° ＋ v y sin 37° 竖直方向有 v ＝ 2 g ( h － h 1 ) 代入数据后解得 v K ＝ 10.4 m/s 代入数据后解得 l ＝ 4.04 m 运动员不脱离圆形轨道顺利通过最高点，雪道 GH 的最大长度为 4.04 m 。 答案 　 (1)7.6 m 　 (2)0.67 m 　 (3)4.04 m [ 精典题组 ] 7. ( 2018· 浙江瑞安选考模拟 ) 如图 9 所示，某一兴趣小组对遥控汽车的性能进行研究，遥控汽车从斜面上 A 点由静止出发，遥控汽车的功率恒为 7 W ，到达 C 点后关闭电源，在 B 点没有动能损失，水平面 BC 在 C 点与光滑半圆轨道 CD 平滑连接，遥控汽车刚好能通过最高点 D 。遥控汽车的质量为 m ＝ 0.2 kg ，汽车与 AB 、 BC 面的动摩擦因数均为 μ ＝ 0.25 ， AB 的长度为 L ＝ 5 m ， AB 的倾角为 37° ， BC 的长度为 s ＝ 8 m ， CD 为半圆轨道的直径， CD 的长度为 d ＝ 3.2 m ，不计空气阻力 (sin 37° ＝ 0.6 ， cos 37° ＝ 0.8 ， g ＝ 10 m/s 2 ) 。求 ： 图 9 (1) 小车离开 D 点后的水平位移大小； (2) 经过 C 点时对圆形轨道的压力是多大？ (3) 从 A 点出发运动到 C 点经历了多长时间 ？ 水平方向位移 x ＝ v D t 得 x ＝ 3.2 m 。 (2) 从 C 点到 D 点的过程中机械能守恒，则 有 8. (2018· 浙江苍南中学高二质检 ) 如图 10 所示，在某电视台举办的冲关游戏中， AB 是处于竖直平面内的光滑圆弧轨道，半径 R ＝ 1.6 m ， BC 是长度为 L 1 ＝ 3 m 的水平传送带， CD 是长度为 L 2 ＝ 3.6 m 水平粗糙轨道， AB 、 CD 轨道与传送带平滑连接，参赛者抱紧滑板从 A 处由静止下滑，参赛者和滑板可视为质点，参赛者质量 m ＝ 60 kg ，滑板质量可忽略。已知滑板与传送带、水平轨道的动摩擦因数分别为 μ 1 ＝ 0.4 、 μ 2 ＝ 0.5 ， g 取 10 m/s 2 。求： 图 10 (1) 参赛者运动到圆弧轨道 B 处对轨道的压力； (2) 若参赛者恰好能运动至 D 点，求传送带运转速率及方向； (3) 在第 (2) 问中，传送带由于传送参赛者多消耗的电能。 解析 　 (1) 对参赛者 A 到 B 过程，由 动能定理 解得 v C ＝ 6 m/s B 到 C 过程，由牛顿第二定律 μ 1 mg ＝ ma 解得 a ＝ 4 m/s 2 参赛者从 B 到 C 先匀加速后匀速，传送带顺时针运转，速率 v ＝ 6 m/s 。 (3)0.5 s 内传送带位移 x 2 ＝ v t ＝ 3 m 参赛者与传送带的相对位移 Δ x ＝ x 2 － x 1 ＝ 0.5 m 传送带由于传送参赛者多消耗的 电能 答案 　 (1)1 200 N 　方向竖直向下　 (2) 顺时针运转　 6 m/s 　 (3)720 J