专题32+电磁感应中的“单杆”模型（精练）-2019年高考物理双基突破（二） 10页

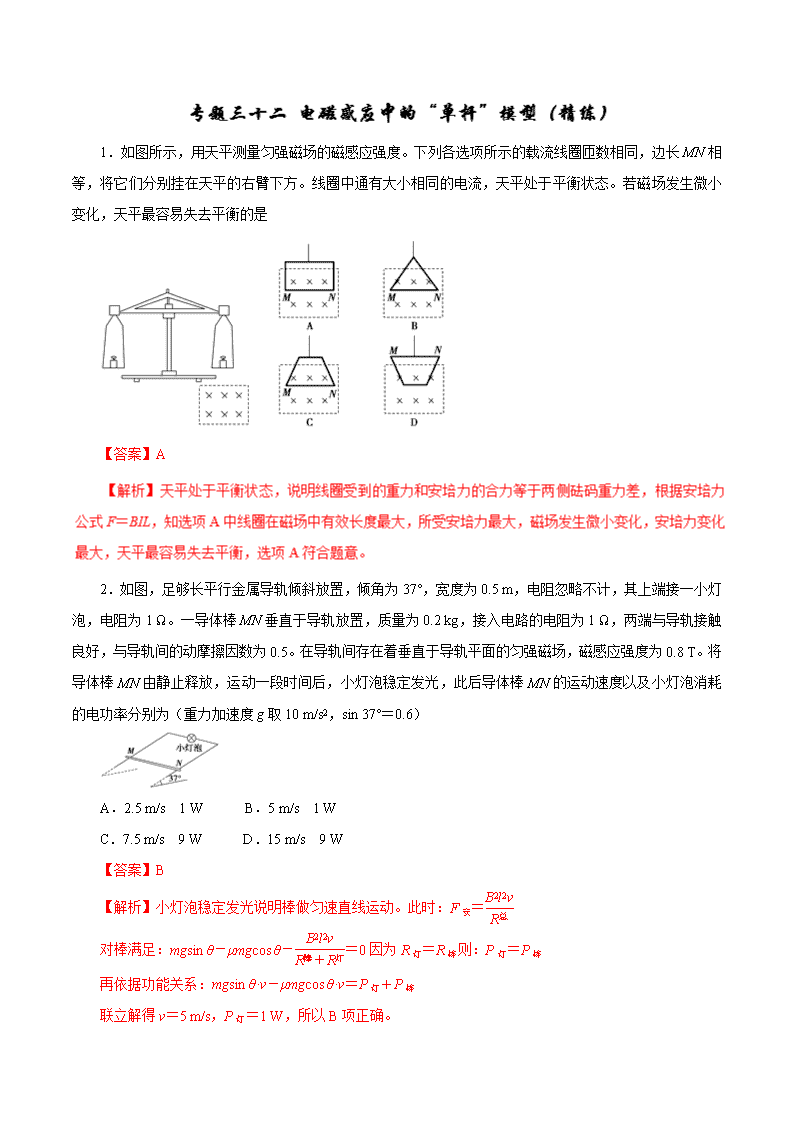
‎1．如图所示，用天平测量匀强磁场的磁感应强度。下列各选项所示的载流线圈匝数相同，边长MN相等，将它们分别挂在天平的右臂下方。线圈中通有大小相同的电流，天平处于平衡状态。若磁场发生微小变化，天平最容易失去平衡的是 ‎ ‎ ‎【答案】A ‎2．如图，足够长平行金属导轨倾斜放置，倾角为37°，宽度为0.5 m，电阻忽略不计，其上端接一小灯泡，电阻为1 Ω。一导体棒MN垂直于导轨放置，质量为0.2 kg，接入电路的电阻为1 Ω，两端与导轨接触良好，与导轨间的动摩擦因数为0.5。在导轨间存在着垂直于导轨平面的匀强磁场，磁感应强度为0.8 T。将导体棒MN由静止释放，运动一段时间后，小灯泡稳定发光，此后导体棒MN的运动速度以及小灯泡消耗的电功率分别为（重力加速度g取10 m/s2，sin 37°＝0.6）‎ A．2.5 m/s　1 W　　　B．5 m/s　1 W C．7.5 m/s　9 W D．15 m/s　9 W ‎【答案】B ‎【解析】小灯泡稳定发光说明棒做匀速直线运动。此时：F安＝ 对棒满足：mgsin θ－μmgcos θ－＝0因为R灯＝R棒则：P灯＝P棒 再依据功能关系：mgsin θ·v－μmgcos θ·v＝P灯＋P棒 联立解得v＝5 m/s，P灯＝1 W，所以B项正确。 ‎ ‎6．（多选）半径为a右端开小口的导体圆环和长为2a的导体直杆，单位长度电阻均为R0。圆环水平固定放置，整个内部区域分布着竖直向下的匀强磁场，磁感应强度为B。杆在圆环上以速度v平行于直径CD向右做匀速直线运动，杆始终有两点与圆环良好接触，从圆环中心O开始，杆的位置由θ确定，如图所示。则 A．θ＝0时，杆产生的电动势为2Bav ‎ B．θ＝时，杆产生的电动势为Bav C．θ＝0时，杆受的安培力大小为 D．θ＝时，杆受的安培力大小为 ‎【答案】AD ‎7．（多选）水平固定放置的足够长的U形金属导轨处于竖直向上的匀强磁场中，如图所示，在导轨上放着金属棒ab，开始时ab棒以水平初速度v0向右运动，最后静止在导轨上，就导轨光滑和粗糙两种情况比较，这个过程 A．产生的总内能相等 ‎ B．通过ab棒的电荷量相等 ‎ C．电流所做的功相等 D．安培力对ab棒所做的功不相等 ‎【答案】AD ‎【解析】两过程中产生的总内能等于金属棒减少的动能，选项A正确；两种情况下，当金属棒速度相等时，在粗糙导轨滑行时的加速度较大，所以导轨光滑时金属棒滑行的较远，根据q＝It＝·t＝＝可知，导轨光滑时通过ab棒的电荷量较大，选项B错误；两个过程中，金属棒减少的动能相等，所以导轨光滑时克服安培力做的功等于导轨粗糙时克服安培力做的功与克服摩擦力做功之和，选项D正确；因为电流所做的功等于克服安培力做的功，所以选项C错误。 ‎ ‎8．（多选）如图所示，在水平桌面上放置两条相距l的平行光滑导轨ab与cd，阻值为R的电阻与导轨的a、c端相连。质量为m、电阻为不计的导体棒垂直于导轨放置并可沿导轨自由滑动。整个装置放于匀强磁场中，磁场的方向竖直向上，磁感应强度的大小为B。导体棒的中点系一个不可伸长的轻绳，绳绕过固定在桌边的光滑轻滑轮后，与一个质量也为m的物块相连，绳处于拉直状态。现若从静止开始释放物块，用h表示物块下落的高度（物块不会触地），g表示重力加速度，其他电阻不计，则 A．电阻R中的感应电流方向由a到c ‎ B．物块下落的最大加速度为g C．若h足够大，物块下落的最大速度为 ‎ D．通过电阻R的电荷量为 ‎【答案】CD ‎9．如图所示，电阻不计的平行金属导轨与水平面间的倾角为θ，下端与阻值为R的定值电阻相连，磁感应强度为B的匀强磁场垂直穿过导轨平面。有一质量为m长为l的导体棒从ab位置获得平行于斜面的、大小为v的初速度向上运动，最远到达a′b′的位置，滑行的距离为s。已知导体棒的电阻也为R，与导轨之间的动摩擦因数为μ，则 A．上滑过程中导体棒受到的最大安培力为 B．上滑过程中电流做功产生的热量为mv2－mgs（sinθ＋μcosθ）‎ C．上滑过程中导体棒克服安培力做的功为mv2‎ D．上滑过程中导体棒损失的机械能为mv2－mgssinθ ‎【答案】BD ‎10．如图甲所示，平行长直金属导轨水平放置，间距L＝0.4 m。导轨右端接有阻值R＝1 Ω的电阻。导体棒垂直放置在导轨上，且接触良好。导体棒及导轨的电阻均不计。导轨间正方形区域abcd内有方向竖直向下的匀强磁场，b、d连线与导轨垂直，长度也为L。从0时刻开始，磁感应强度B的大小随时间t变化，规律如图乙所示；同一时刻，棒从导轨左端开始向右匀速运动，1 s后刚好进入磁场。若使棒在导轨上始终以速度v＝1 m/s做直线运动，求：‎ ‎（1）棒进入磁场前，回路中的电动势E；‎ ‎（2）棒在运动过程中受到的最大安培力F，以及棒通过三角形abd区域时电流i与时间t的关系式。‎ ‎【答案】（1）0.04 V（2）0.04 N i＝t－1（1 s≤t≤1.2 s）‎ ‎【解析】由图乙可知0～1.0 s内B的变化率＝0.5 T/s ①‎ 正方形磁场区域的面积S＝2＝0.08 m2v ②‎ 棒进入磁场前0～1.0 s内回路中感应电动势E＝＝ ③‎ 由①②③得E＝0.08×0.5 V＝0.04 V ‎（2）当棒通过bd位置时，有效切割长度最大，感应电流最大，棒受到最大安培力F＝BIL ④‎ 棒过bd时的感应电动势Em＝BLv＝0.5×0.4×1 V＝0.2 V ⑤‎ 棒过bd时的电流I＝ ⑥‎ 由④⑤⑥得F＝0.04 N 棒通过a点后在三角形abd区域中的有效切割长度L′与时间t的关系：‎ L′＝2v（t－1），其中t的取值范围为1 s≤t≤1.2 s ⑦‎ 电流i与时间t的关系式i＝＝＝t－1（1 s≤t≤1.2 s）。‎ ‎11．如图所示，长平行导轨PQ、MN光滑，相距l＝0.5 m，处在同一水平面中，磁感应强度B＝0.8 T的匀强磁场竖直向下穿过导轨面。横跨在导轨上的直导线ab的质量m＝0.1 kg、电阻R＝0.8 Ω，导轨电阻不计。导轨间通过开关S将电动势E＝1.5 V、内电阻r＝0.2 Ω的电池接在M、P两端，试计算分析：‎ ‎（1）导线ab的加速度的最大值和速度的最大值是多少？‎ ‎（2）在闭合开关S后，怎样才能使ab以恒定的速度v＝7.5 m/s 沿导轨向右运动？试描述这时电路中的能量转化情况（通过具体的数据计算说明）。‎ ‎【答案】（1）3.75 m/s（2）见解析 ab受安培力水平向右，此时ab瞬时加速度最大，加速度a0＝＝＝6 m/s2。‎ 当感应电动势E′与电池电动势E相等时，ab的速度达到最大值。‎ 设最终达到的最大速度为vm，根据上述分析可知：E－Blvm＝0‎ 所以vm＝＝ m/s＝3.75 m/s。‎ ‎（2）如果ab以恒定速度v＝7.5 m/s向右沿导轨运动，则ab中感应电动势E′＝Blv＝0.8×0.5×7.5 V＝3 V 由于E′＞E，这时闭合电路中电流方向为逆时针方向，大小为：I′＝＝ A＝1.5 A 直导线ab 中的电流由b到a，根据左手定则，磁场对ab有水平向左的安培力作用，大小为 F′＝BlI′＝0.8×0.5×1.5 N＝0.6 N 所以要使ab以恒定速度v＝7.5 m/s向右运动，必须有水平向右的恒力F＝0.6 N作用于ab。‎ 上述物理过程的能量转化情况，可以概括为下列三点：‎ ‎①作用于ab的恒力（F）的功率：P＝Fv＝0.6×7.5 W＝4.5 W ‎②电阻（R＋r）产生焦耳热的功率：P′＝I2（R＋r）＝1.52×（0.8＋0.2）W＝2.25 W ‎③逆时针方向的电流I′，从电池的正极流入，负极流出，电池处于“充电”状态，吸收能量，以化学能的形式储存起来。‎ 电池吸收能量的功率：P″＝I′E＝1.5×1.5 W＝2.25 W 由上看出，P＝P′＋P″，符合能量转化和守恒定律（沿水平面匀速运动机械能不变）。‎ ‎12．如图所示，水平面内有两根足够长的平行导轨L1、L2，其间距d＝0.5 m，左端接有容量C＝2 000 μF的电容。质量m＝20 g的导体棒可在导轨上无摩擦滑动，导体棒和导轨的电阻不计。整个空间存在着垂直导轨所在平面的匀强磁场，磁感应强度B＝2 T。现用一沿导轨方向向右的恒力F1＝0.44 N作用于导体棒，使导体棒从静止开始运动，经t时间后到达B处，速度v＝5 m/s。此时，突然将拉力方向变为沿导轨向左，大小变为F2，又经2t时间后导体棒返回到初始位置A处，整个过程电容器未被击穿。求 ‎（1）导体棒运动到B处时，电容C上的电量；‎ ‎（2）t的大小；‎ ‎（3）F2的大小。‎ ‎【答案】（1）1×10－2 C（2）0.25 s（3）0.55 N ‎（2）棒在F1作用下有F1－BId＝ma1，‎ 又I＝＝，a1＝ 联立解得：a1＝＝20 m/s2则t＝＝0.25 s。‎ ‎（3）由（2）可知棒在F2作用下，运动的加速度a2＝，方向向左，‎ 又a1t2＝－（a1t·2t－）‎ 将相关数据代入解得F2＝0.55 N。‎ ‎13．如图所示，在匀强磁场中有一倾斜的平行金属导轨，导轨间距为L，长为3d，导轨平面与水平面的夹角为θ，在导轨的中部刷有一段长为d的薄绝缘涂层。匀强磁场的磁感应强度大小为B，方向与导轨平面垂直。质量为m的导体棒从导轨的顶端由静止释放，在滑上涂层之前已经做匀速运动，并一直匀速滑到导轨底端。导体棒始终与导轨垂直，且仅与涂层间有摩擦，接在两导轨间的电阻为R，其他部分的电阻均不计，重力加速度为g。求：‎ ‎（1）导体棒与涂层间的动摩擦因数μ；‎ ‎（2）导体棒匀速运动的速度大小v；‎ ‎（3）整个运动过程中，电阻产生的焦耳热Q。‎ ‎【答案】（1）tan θ（2）（3）2mgdsin θ－.‎ ‎14．如图甲所示，一对足够长的平行光滑轨道固定在水平面上，两轨道间距l＝0.5m，左侧接一阻值为R＝1Ω的电阻。有一金属棒静止地放在轨道上，与两轨道垂直，金属棒及轨道的电阻皆可忽略不计，整个装置处于垂直轨道平面竖直向下的匀强磁场中。t＝0时，用一外力F 沿轨道方向拉金属棒，使金属棒以加速度a＝0.2m/s2做匀加速运动，外力F与时间t的关系如图乙所示。‎ ‎（1）求金属棒的质量m；‎ ‎（2）求磁感应强度B；‎ ‎（3）当力F达到某一值时，保持F不再变化，金属棒继续运动3s，速度达到1.6m/s且不再变化，测得在这3s内金属棒的位移s＝4.7m，求这段时间内电阻R消耗的电能。‎ ‎【答案】（1）0.5kg　（2）1T　（3）1.6J ‎（3）F变为恒力后，金属棒做加速度逐渐减小的变加速运动，经过3s后，速度达到最大vm＝1.6m/s，此后金属棒做匀速运动。‎ vm＝1.6m/s时，F合＝0，F＝F安＝＝＝0.4（N）‎ 将F＝0.4N代入F＝0.1＋0.05t，求出金属棒做变加速运动的起始时间为：t＝6s 该时刻金属棒的速度为v1＝at＝0.2×6＝1.2（m/s）‎ 这段时间内电阻R消耗的电能 E＝WF－ΔEk＝Fs－m（v－v）＝0.4×4.7－×0.5×（1.62－1.22）＝1.6（J）。 ‎ ‎15．（1）如图甲所示，两根足够长的平行导轨，间距L＝0.3m，在导轨间有垂直纸面向里的匀强磁场，磁感应强度B1＝0.5T。一根直金属杆MN以v＝2m/s的速度向右匀速运动，杆MN始终与导轨垂直且接触良好。杆MN的电阻r1＝1Ω，导轨的电阻可忽略。求杆MN中产生的感应电动势E1。‎ ‎（2）如图乙所示，一个匝数n＝100的圆形线圈，面积S1＝0.4m2，电阻r2＝1Ω。在线圈中存在面积S2＝0.3m2垂直线圈平面（指向纸外）的匀强磁场区域，磁感应强度B2随时间t变化的关系如图丙所示。求圆形线圈中产生的感应电动势E2。‎ ‎（3）有一个R＝2Ω的电阻，将其两端a、b分别与图甲中的导轨和图乙中的圆形线圈相连接，b端接地。试判断以上两种情况中，哪种情况a端的电势较高？求这种情况中a端的电势φa。‎ ‎【答案】（1）0.3V　（2）4.5V　（3）与图甲中的导轨相连接a端电势高　φa＝0.2V ‎（3）当电阻R与题图甲中的导轨相连接时，a端的电势较高 通过电阻R的电流I＝ 电阻R两端的电势差φa－φb＝IR a端的电势φa＝IR＝0.2V。‎ ‎16．如图甲所示，水平面上的两光滑金属导轨平行固定放置，间距d＝0.5 m，电阻不计，左端通过导线与阻值R＝2 Ω的电阻连接，右端通过导线与阻值RL＝4 Ω的小灯泡L连接．在CDEF矩形区域内有竖直向上的匀强磁场，CE长l＝2 m，有一阻值r＝2 Ω的金属棒PQ放置在靠近磁场边界CD处（恰好不在磁场中）。CDEF区域内磁场的磁感应强度B随时间变化如图乙所示。在t＝0至t＝4 s内，金属棒PQ保持静止，在t＝4 s时使金属棒PQ以某一速度进入磁场区域并保持匀速运动。已知从t＝0开始到金属棒运动到磁场边界EF处的整个过程中，小灯泡的亮度没有发生变化，求：‎ ‎（1）通过小灯泡的电流；‎ ‎（2）金属棒PQ在磁场区域中运动的速度大小。‎ ‎【答案】（1）0.1 A　（2）1 m/s ‎（2）当棒在磁场区域中运动时，由导体棒切割磁感线产生电动势，电路为R与RL并联，再与r串联，此时电路的总电阻R总′＝r＋＝2＋ Ω＝ Ω 由于灯泡中电流不变，所以灯泡的电流IL＝0.1A，则流过棒的电流为I′＝IL＋IR＝IL＋＝0.3 A 电动势E′＝I′R总′＝Blv 解得棒PQ在磁场区域中运动的速度大小v＝1 m/s ‎