- 1012.67 KB
- 2021-05-23 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
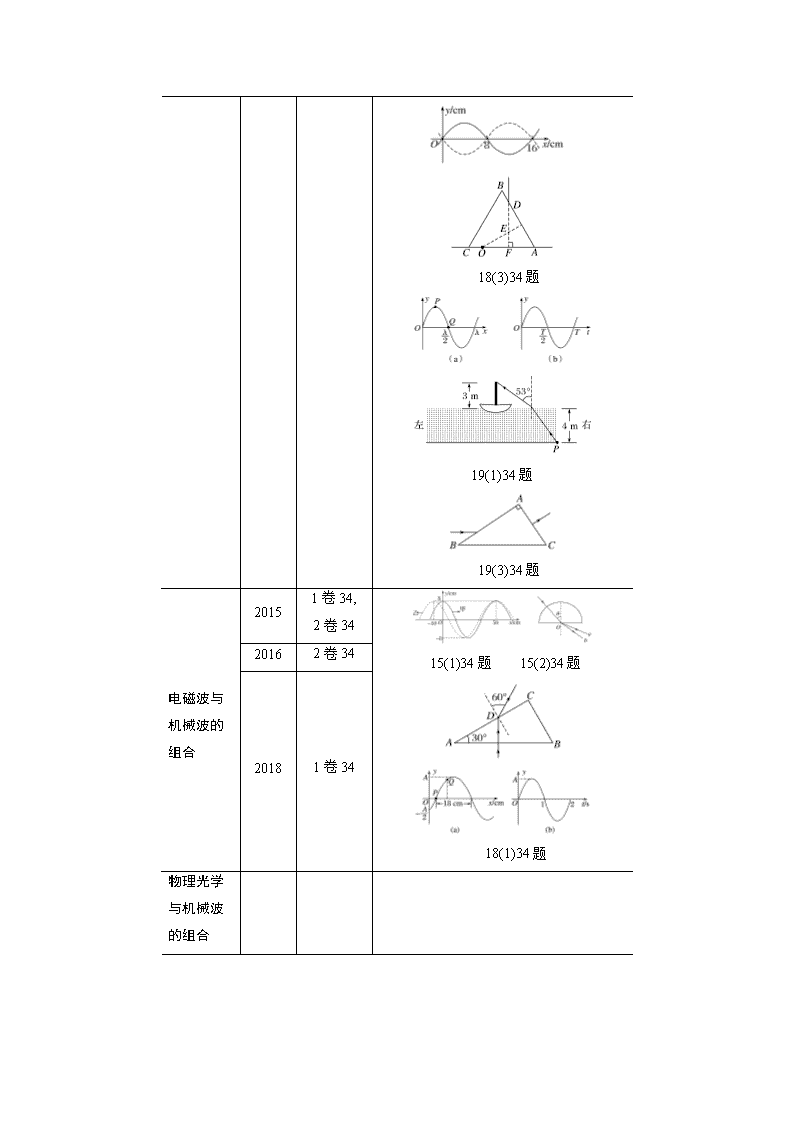
第2课时 机械振动和机械波 光
高考命题点
命题轨迹
情境图
机械振动和机械波与光的组合
2016
1卷34,
3卷34
16(1)34题 16(3)34题
17(1)34题
17(2)34题
17(3)34题
18(2)34题
18(3)34题
19(1)34题
19(3)34题
2017
1卷34,
2卷34,
3卷34
2018
2卷34,
3卷34
2019
1卷34,3卷34
电磁波与机械波的组合
2015
1卷34,
2卷34
15(1)34题 15(2)34题
18(1)34题
2016
2卷34
2018
1卷34
物理光学与机械波的组合
3-4模块实验
2019
2卷34
19(2)34题
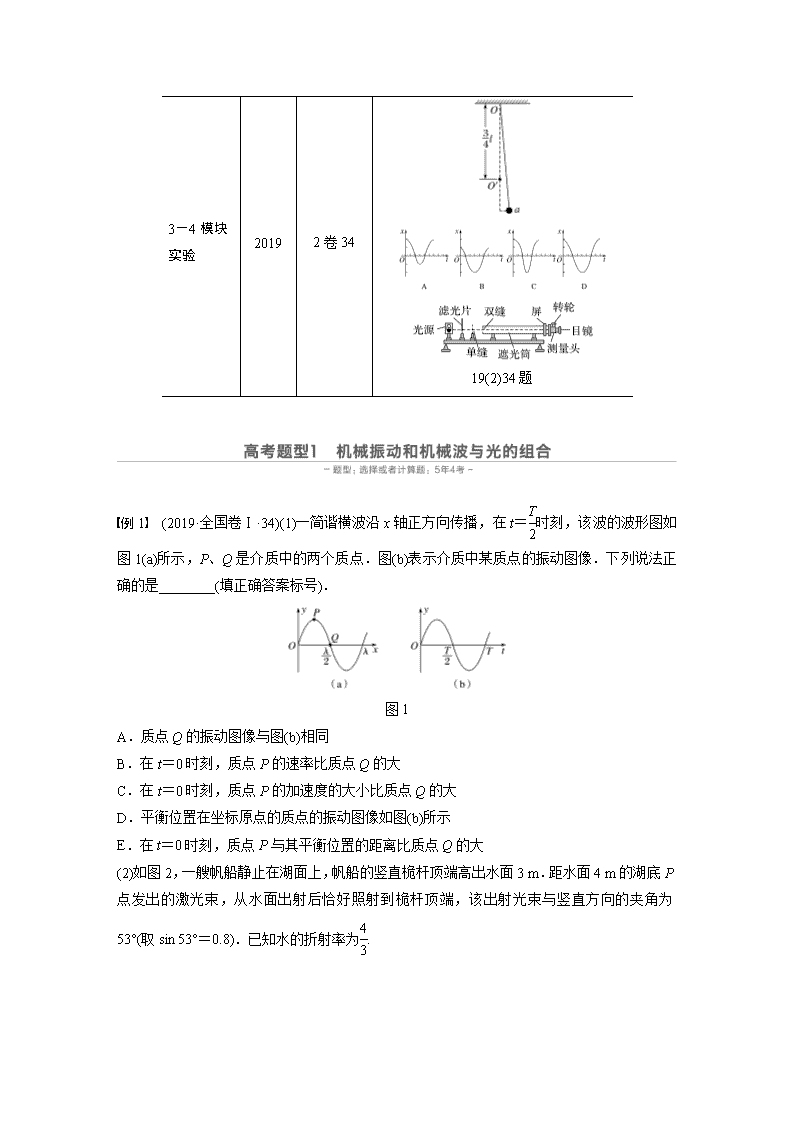
例1 (2019·全国卷Ⅰ·34)(1)一简谐横波沿x轴正方向传播,在t=时刻,该波的波形图如图1(a)所示,P、Q是介质中的两个质点.图(b)表示介质中某质点的振动图像.下列说法正确的是________(填正确答案标号).
图1
A.质点Q的振动图像与图(b)相同
B.在t=0时刻,质点P的速率比质点Q的大
C.在t=0时刻,质点P的加速度的大小比质点Q的大
D.平衡位置在坐标原点的质点的振动图像如图(b)所示
E.在t=0时刻,质点P与其平衡位置的距离比质点Q的大
(2)如图2,一艘帆船静止在湖面上,帆船的竖直桅杆顶端高出水面3 m.距水面4 m的湖底P点发出的激光束,从水面出射后恰好照射到桅杆顶端,该出射光束与竖直方向的夹角为53°(取sin 53°=0.8).已知水的折射率为.
图2
①求桅杆到P点的水平距离;
②船向左行驶一段距离后停止,调整由P点发出的激光束方向,当其与竖直方向夹角为45°时,从水面射出后仍照射在桅杆顶端,求船行驶的距离.
答案 (1)CDE (2)①7 m ②5.5 m
解析 (1)t=时刻,题图(b)表示介质中的某质点从平衡位置向下振动,而题图(a)中质点Q在t=时刻从平衡位置向上振动,平衡位置在坐标原点的质点从平衡位置向下振动,所以质点Q的振动图像与题图(b)不同,平衡位置在坐标原点的质点的振动图像如题图(b)所示,选项A错误,D正确;在t=0时刻,质点P处在波谷位置,速率为零,与其平衡位置的距离最大,加速度最大,而质点Q运动到平衡位置,速率最大,加速度为零,即在t=0时刻,质点P的速率比质点Q的小,质点P的加速度比质点Q的大,质点P与其平衡位置的距离比质点Q的大,选项B错误,C、E正确.
(2)①设光束从水面射出的点到桅杆的水平距离为x1,到P点的水平距离为x2;桅杆距水面的高度为h1,P点处水深为h2;激光束在水中与竖直方向的夹角为θ,由几何关系有
=tan 53°①
=tan θ②
由折射定律有:sin 53°=nsin θ③
设桅杆到P点的水平距离为x,
则x=x1+x2④
联立①②③④式并代入题给数据得:x=7 m⑤
②设激光束在水中与竖直方向的夹角为45°时,从水面出射的方向与竖直方向夹角为i′
由折射定律有:sin i′=nsin 45°⑥
设船向左行驶的距离为x′,此时光束从水面射出的点到桅杆的水平距离为x1′,到P点的水平距离为x2′,则:x1′+x2′=x′+x⑦
=tan i′⑧
=tan 45°⑨
联立⑤⑥⑦⑧⑨式并代入题给数据得:
x′= m≈5.5 m⑩
拓展训练1 (2019·全国卷Ⅲ·34)(1)水槽中,与水面接触的两根相同细杆固定在同一个振动片上.振动片做简谐振动时,两根细杆周期性触动水面形成两个波源.两波源发出的波在水面上相遇,在重叠区域发生干涉并形成了干涉图样.关于两列波重叠区域内水面上振动的质点,下列说法正确的是________.
A.不同质点的振幅都相同
B.不同质点振动的频率都相同
C.不同质点振动的相位都相同
D.不同质点振动的周期都与振动片的周期相同
E.同一质点处,两列波的相位差不随时间变化
(2)如图3,直角三角形ABC为一棱镜的横截面,∠A=90°,∠B=30°.一束光线平行于底边BC射到AB边上并进入棱镜,然后垂直于AC边射出.
图3
①求棱镜的折射率;
②保持AB边上的入射点不变,逐渐减小入射角,直到BC边上恰好有光线射出.求此时AB边上入射角的正弦.
答案 (1)BDE (2)① ②
解析 (1)在波的干涉实验中,质点在振动加强区的振幅是两列波振幅之和,质点在振动减弱区的振幅是两列波振幅之差,A项错误;沿波的传播方向上,波不停地向外传播,故各质点的相位不都相同,C项错误;两波源振动频率相同,其他各质点均做受迫振动,故频率均与振源频率相同,周期均与振动片的周期相同,B、D项正确;同一质点到两波源的距离确定,故波程差恒定,即相位差保持不变,E正确.
(2)①光路图及相关量如图所示.光束在AB边上折射,由折射定律得
=n①
式中n是棱镜的折射率.由几何关系可知
α+β=60°②
由几何关系和反射定律得
β=β′=∠B③
联立①②③式,并代入i=60°得
n=④
②设改变后的入射角为i′,折射角为α′,由折射定律得
=n⑤
依题意,光束在BC边上的入射角为全反射的临界角θc,且sin θc=⑥
由几何关系得θc=α′+30°⑦
由④⑤⑥⑦式得入射角的正弦为
sin i′=
拓展训练2 (2019·河南安阳市下学期二模)(1)如图4甲所示为一列简谐横波在t=2 s时的波形图,图乙为介质中平衡位置在x=1.5 m处的质点的振动图象.P是平衡位置在x=2 m处的质点,则下列说法正确的是( )
图4
A.t=2 s时,x=1.5 m处质点的振动速度为0.5 m/s
B.t=2 s时,x=1.0 m处质点的位移为4 cm
C.该简谐横波沿x轴的负方向传播
D.0~1 s时间内,P向y轴正方向运动
E.0~3 s时间内,P运动的路程为12 cm
(2)如图5所示,一容器内装有深为h的某透明液体,容器底部为平面镜,到容器底部的距离为处有一点光源L,可向各个方向发光.已知该透明液体的折射率为n,液面足够宽,真空中光的传播速度为c,求:
图5
①能从液面射出的光,在液体中经过的最短时间t;
②液面上有光射出的区域的面积S.
答案 (1)BCE (2)① ②
解析 (1)由题图可知波长λ=2 m,T=4 s,则波速v==0.5 m/s;此为波的传播速度,并非质点的振动速度,选项A错误;质点的振幅为4 cm,t=2 s时,x=1 m处质点位于波峰位置,位移为A=4 cm,选项B正确;t=2 s时,x=1.5 m处质点沿y轴负方向运动,则该波沿x轴负方向传播,选项C正确;0~1 s时间内,质点P由波峰向平衡位置运动,沿y轴负方向运动,选项D错误;t=0时,质点P位于波峰,故经过3 s质点P经过的路程为s=3A=12 cm,选项E正确.
(2)①光在液体中的速度为v=
在液体中垂直液面射出时经过的时间t最短,则有=vt
解得:t=;
②设光在液面上发生全反射的临界角为C,则有sin C=
液面有光射出的区域为圆形,设其半径为r,则由于容器底面为平面镜,有r=tan C
解得:r=
液面上有光射出的区域的面积S=πr2
解得:S=.
例2 (2019·山东济南市3月模拟)(1)如图6甲所示,在平静的水面下深h处有一个点光源S,它发出的两种不同颜色的a光和b光在水面上形成了一个有光线射出的圆形区域,该区域的中间为由a、b两种单色光所构成的复色光圆形区域,周围为环状区域,且为a光的颜色(见图乙),设b光的折射率为nb,则下列说法正确的是________.
图6
A.在水中,a光的波长比b光小
B.水对a光的折射率比b光小
C.在水中,a光的传播速度比b光大
D.复色光圆形区域的面积为S=
E.在同一装置的杨氏双缝干涉实验中,a光的干涉条纹比b光窄
(2)有两列简谐横波a、b在同一介质中沿x轴正方向传播,速度均为v=5 m/s.在t=0时,两列波的波峰正好在x=2.5 m处重合,如图7所示.
图7
①求t=0时,两列波的波峰重合处的所有位置;
②至少经多长时间x=0处的质点位移达到最大值.
答案 (1)BCD (2)①x=(2.5±20n) m(n=0,1,2,3,…) ②3.5 s
解析 (1)a光在水面上形成的圆形亮斑面积较大,知a光的临界角较大,根据sin C=,知a光的折射率较小,频率也小,再由v==λf可知,在水中,a光的传播速度比b光大,a光的波长比b光大,故B、C正确,A错误;依据sin C=,结合几何关系,可知,=,故复色光圆形区域的面积为S=πr2=,故D正确;a光的折射率小,波长长,根据双缝干涉条纹与波长成正比,可知相同条件下,a光的干涉条纹比b光宽,故E错误.
(2)①从题图中可以看出两列波的波长分别为:
λa=2.5 m,λb=4.0 m
两列波波长的最小公倍数为:s=20 m
t=0时,两列波的波峰重合处的所有位置为:x=(2.5±20n) m(n=0,1,2,3…)
②在x=0左侧,x=0处的质点离两列波的波峰重合处最近点的距离为:Δx=17.5 m(或者写出:x=-17.5 m)
x=0处的质点位移达到最大值至少需用时:Δt=
解得:Δt=3.5 s.
拓展训练3 (2019·东北三省四市教研联合体模拟)(1)插针法测量半圆形玻璃砖的折射率.将半圆形玻璃砖平放在白纸上,在白纸上先画出玻璃砖的轮廓,并确定其圆心O的位置.再画出一条通过圆心O的直线,将两枚大头针P1、P2 竖直插在这条直线上,如图8所示.
图8
①为了确定入射光线P2P1的折射光线方向,至少需要在玻璃砖另一侧插入________枚大头针;
②若测得入射光线与ON的夹角为α,折射光线与OM的夹角为β,则该玻璃砖的折射率为________.
(2)甲、乙两列横波传播速度相同,分别沿x轴负方向和x轴正方向传播,t0时刻两列波的前端刚好分别传播到质点A和质点B,如图9所示,设t0时刻为计时起点,已知甲波的频率为5 Hz,求:
图9
①t0时刻之前,x轴上的质点C振动了多长时间?
②在t0时刻之后的0.9 s内,x=0处的质点位移为+6 cm的时刻.
答案 (1)①1 ② (2)①0.1 s ②0.2 s和0.6 s
解析 (1)①作出光路图,如图
由图可知只需要一根大头针就可以确定出折射光线;
②由题图可知,入射角i=90°-α,折射角r=90°-β,
根据折射定律得:n===.
(2)①由题中条件可知,甲波的周期为:T甲==0.2 s
由题图知λ甲=4 m,λ乙=8 m
波速为:v=λ甲f甲=20 m/s
乙波的周期为:T乙==0.4 s
由题图可知,C点开始振动的时刻距图中时刻为:
tC=T乙=0.1 s
即t0时刻之前,质点C已振动了0.1 s.
②x=0处的质点位移为+6 cm,表明两列波的波峰同时到达x=0处.
甲波的波峰到达x=0处的时刻为:
t甲=mT甲(m=0、1、2、3…)
乙波的波峰到达x=0处的时刻为:
t乙=(n+)T乙(n=0、1、2、3…)
t甲=t乙
解得:m=2n+1
n=0时,m=1,t=0.2 s
n=1时,m=3,t=0.6 s
n=2时,m=5,t=1 s
可知:在之后的0.9 s内,x=0处的质点位移为+6 cm的时刻为0.2 s和0.6 s.
拓展训练4 (2019·四川达州市第二次诊断)(1)直线P1P2过均匀玻璃球球心O,细光束a、b平行且关于P1P2对称,由空气射入玻璃球的光路如图10所示.a、b光相比________.
图10
A.玻璃对a光的折射率较小
B.b光在玻璃中的传播速度较大
C.b光在玻璃中的传播时间较长
D.用同一双缝干涉实验装置做实验,a光的相邻两明条纹之间的距离大
E.用同一衍射实验装置做实验,b光的衍射条纹宽度相等且比a光的宽
(2)如图11,一列简谐横波沿x轴传播,实线为t1=0时刻的波形图,虚线为t2=0.05 s时的波形图.
图11
①若波沿x轴正方向传播且2T