【物理】2020届一轮复习人教版水平面内的圆周运动作业 11页

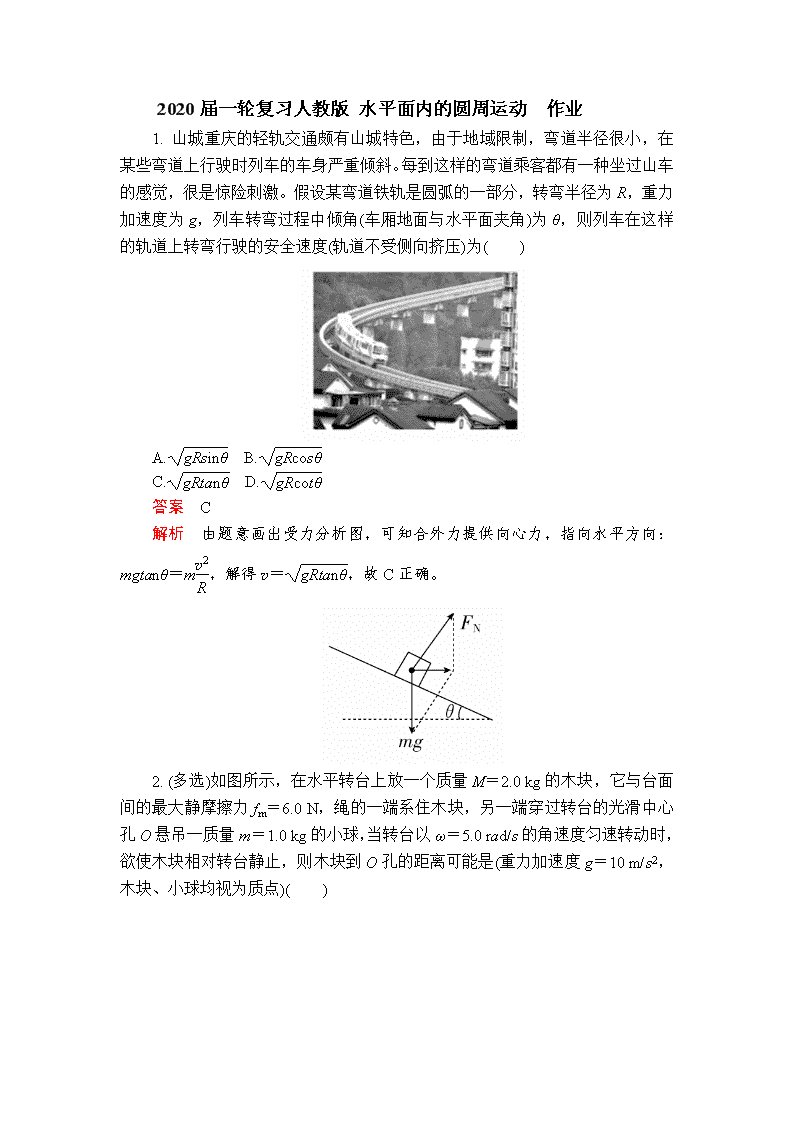
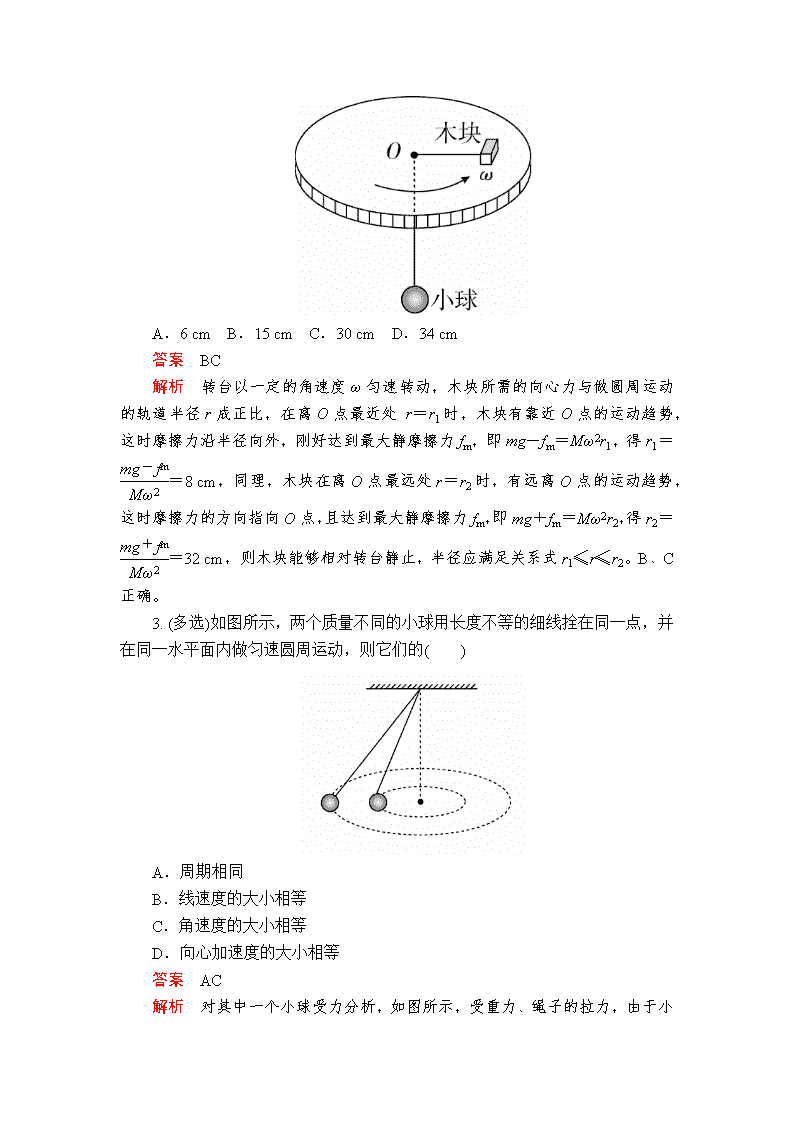
‎2020届一轮复习人教版 水平面内的圆周运动 作业 ‎1. 山城重庆的轻轨交通颇有山城特色，由于地域限制，弯道半径很小，在某些弯道上行驶时列车的车身严重倾斜。每到这样的弯道乘客都有一种坐过山车的感觉，很是惊险刺激。假设某弯道铁轨是圆弧的一部分，转弯半径为R，重力加速度为g，列车转弯过程中倾角(车厢地面与水平面夹角)为θ，则列车在这样的轨道上转弯行驶的安全速度(轨道不受侧向挤压)为(　　)‎ A. B. C. D. 答案　C 解析　由题意画出受力分析图，可知合外力提供向心力，指向水平方向：mgtanθ＝m，解得v＝，故C正确。‎ ‎2. (多选)如图所示，在水平转台上放一个质量M＝‎2.0 kg的木块，它与台面间的最大静摩擦力fm＝6.0 N，绳的一端系住木块，另一端穿过转台的光滑中心孔O悬吊一质量m＝‎1.0 kg的小球，当转台以ω＝5.0 rad/s的角速度匀速转动时，欲使木块相对转台静止，则木块到O孔的距离可能是(重力加速度g＝‎10 m/s2，木块、小球均视为质点)(　　)‎ A．‎6 cm B．‎15 cm C．‎30 cm D．‎‎34 cm 答案　BC 解析　转台以一定的角速度ω匀速转动，木块所需的向心力与做圆周运动的轨道半径r成正比，在离O点最近处 r＝r1时，木块有靠近O点的运动趋势，这时摩擦力沿半径向外，刚好达到最大静摩擦力fm，即mg－fm＝Mω2r1，得r1＝＝‎8 cm，同理，木块在离O点最远处r＝r2时，有远离O点的运动趋势，这时摩擦力的方向指向O点，且达到最大静摩擦力fm，即mg＋fm＝Mω2r2，得r2＝＝‎32 cm，则木块能够相对转台静止，半径应满足关系式r1≤r≤r2。B、C正确。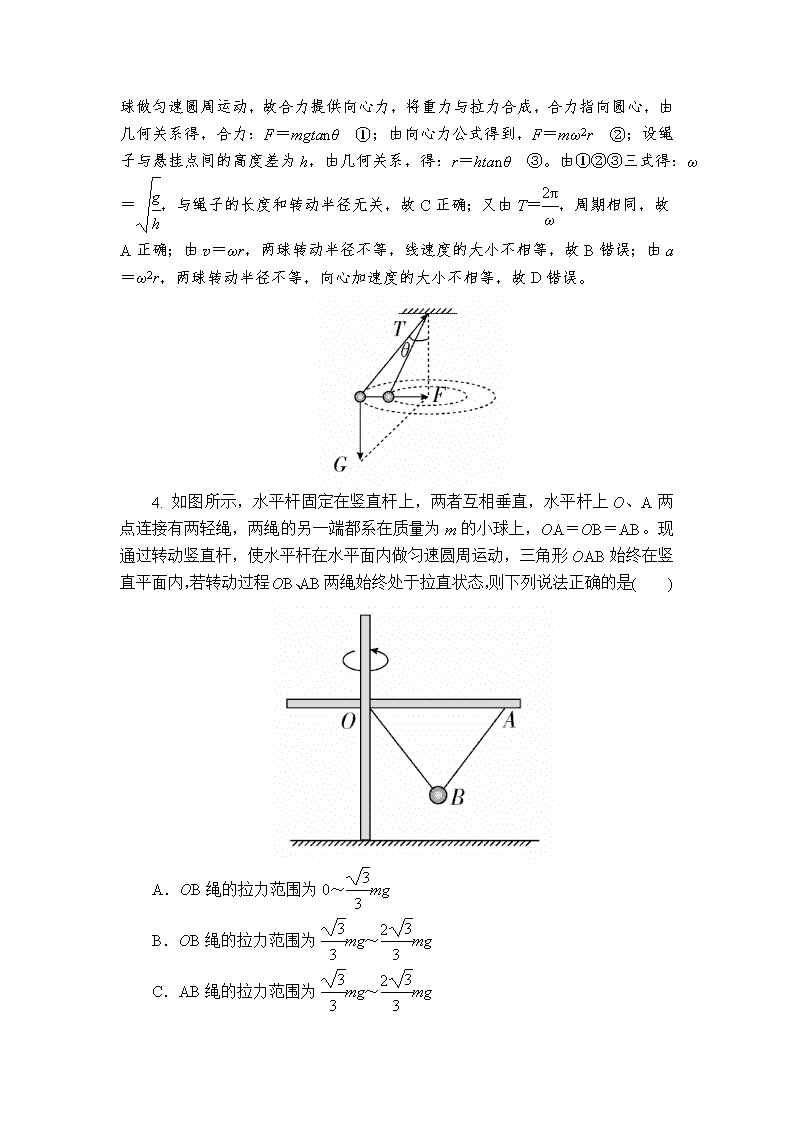‎ ‎3. (多选)如图所示，两个质量不同的小球用长度不等的细线拴在同一点，并在同一水平面内做匀速圆周运动，则它们的(　　)‎ A．周期相同 B．线速度的大小相等 C．角速度的大小相等 D．向心加速度的大小相等 答案　AC 解析　对其中一个小球受力分析，如图所示，受重力、绳子的拉力，由于小 球做匀速圆周运动，故合力提供向心力，将重力与拉力合成，合力指向圆心，由几何关系得，合力：F＝mgtanθ　①；由向心力公式得到，F＝mω2r　②；设绳子与悬挂点间的高度差为h，由几何关系，得：r＝htanθ　③。由①②③三式得：ω＝，与绳子的长度和转动半径无关，故C正确；又由T＝，周期相同，故A正确；由v＝ωr，两球转动半径不等，线速度的大小不相等，故B错误；由a＝ω2r，两球转动半径不等，向心加速度的大小不相等，故D错误。‎ ‎4. 如图所示，水平杆固定在竖直杆上，两者互相垂直，水平杆上O、A两点连接有两轻绳，两绳的另一端都系在质量为m的小球上，OA＝OB＝AB。现通过转动竖直杆，使水平杆在水平面内做匀速圆周运动，三角形OAB始终在竖直平面内，若转动过程OB、AB两绳始终处于拉直状态，则下列说法正确的是(　　)‎ A．OB绳的拉力范围为0～mg B．OB绳的拉力范围为mg～mg C．AB绳的拉力范围为mg～mg D．AB绳的拉力范围为0～mg 答案　B 解析　当转动的角速度为零时，OB绳的拉力最小，AB绳的拉力最大，这时两者的值相同，设为F1，则‎2F1cos30°＝mg，F1＝mg，增大转动的角速度，当AB绳的拉力刚好等于零时，OB绳的拉力最大，设这时OB绳的拉力为F2，则F2cos30°＝mg，F2＝mg，因此OB绳的拉力范围为mg～mg，AB绳的拉力范围为0～mg，B正确。‎ ‎5. 如图所示，“旋转秋千”中的两个座椅A、B质量相等，通过相同长度的缆绳悬挂在旋转圆盘上。不考虑空气阻力的影响，当旋转圆盘绕竖直的中心轴匀速转动时，下列说法正确的是(　　)‎ A．A的速度比B的大 B．A与B的向心加速度大小相等 C．悬挂A、B的缆绳与竖直方向的夹角相等 D．悬挂A的缆绳所受的拉力比悬挂B的小 答案　D 解析　设转动时，座椅悬点到转轴距离为d，绳长为l，与竖直方向的夹角为θ，则mgtanθ＝m(d＋lsinθ)ω2，整理得d＝tanθ－lsinθ，由此可知d越大，θ越大，C错误；v＝rω＝(d＋lsinθ)ω，d越大，θ越大，则v越大，A错误；向心加速度a＝gtanθ，B错误；绳的拉力T＝，故悬挂A的缆绳所受拉力较小，D正确。‎ ‎[真题模拟练]‎ ‎6. (2016·浙江高考)(多选)如图所示为赛车场的一个水平“梨形”赛道，两个弯道分别为半径R＝‎90 m的大圆弧和r＝‎40 m的小圆弧，直道与弯道相切。大、小圆弧圆心O、O′距离L＝‎100 m。赛车沿弯道路线行驶时，路面对轮胎的最大径向静摩擦力是赛车重力的2.25倍。假设赛车在直道上做匀变速直线运动，在弯道上做匀速圆周运动。要使赛车不打滑且绕赛道一圈时间最短(发动机功率足够大，重力加速度g＝‎10 m/s2，π＝3.14)，则赛车(　　)‎ A．在绕过小圆弧弯道后加速 B．在大圆弧弯道上的速率为‎45 m/s C．在直道上的加速度大小为‎5.63 m/s2‎ D．通过小圆弧弯道的时间为5.58 s 答案　AB 解析　赛车做圆周运动时，由F＝知，在小圆弧上的速度小，故赛车绕过小圆弧后加速，A正确；在大圆弧弯道上时，根据F＝m知，其速率v＝ ＝ ＝‎45 m/s，B正确；同理可得在小圆弧弯道上的速率v′＝‎30 m/s。如图所示，由边角关系可得α＝60°，直道的长度x＝Lsin60°＝‎50 m，据v2－v′2＝2‎ ax知在直道上的加速度a≈‎6.50 m/s2，C错误；小弯道对应的圆心角为120°，弧长为s＝，对应的运动时间t＝≈2.79 s，D错误。‎ ‎7．(2018·兰化一中模拟) 如图所示，“旋转秋千”中座椅(可视为质点)通过轻质缆绳悬挂在旋转圆盘上。当旋转圆盘以角速度ω匀速转动时，不计空气阻力，缆绳延长线与竖直中心轴相交于O点，夹角为θ，O点到座椅的竖直高度为h，则当ω增大时(　　)‎ A．h不变 B．θ减小 C．ω2h不变 D．ω2h增大 答案　C 解析　对座椅受力分析如图所示，根据牛顿第二定律可得mgtanθ＝mω2htanθ，解得：g＝ω2h，则当ω增大时，h减小，θ变大，ω2h不变，故选C。‎ ‎8. (2018·三门峡陕州中学专训)在玻璃管中放一个乒乓球后注满水，然后用软木塞封住管口，将此玻璃管固定在转盘上，管口置于转盘转轴处，处于静止状态。当转盘在水平面内转动时，如图所示，则乒乓球会(球直径比管直径略小)(　　)‎ A．向管底运动 B．向管口运动 C．保持不动 D．无法判断 答案　B 解析　开始时，玻璃管壁的摩擦力不足以提供水做圆周运动时所需要的向心力，所以水被“甩”到外侧管底才能随转盘进行圆周运动，则乒乓球在水的作用下向管口运动，故B正确。‎ ‎9. (2018·宝鸡一模)(多选)如图所示，一个内壁光滑的圆锥筒固定在地面上，圆锥筒的轴线竖直。一个小球贴着筒的内壁在水平面内做圆周运动，由于微弱的空气阻力作用，小球的运动轨迹由A轨道缓慢下降到B轨道，则在此过程中(　　)‎ A．小球的向心加速度逐渐减小 B．小球运动的角速度逐渐减小 C．小球运动的线速度逐渐减小 D．小球运动的周期逐渐减小 答案　CD 解析　以小球为研究对象，对小球受力分析，小球受力如图所示。由牛顿第二定律得：＝ma＝m＝mrω2，可知在A、B轨道的向心力大小相等，a＝，向心加速度不变，故A错误。角速度ω＝ ，由于半径减小，则角速度变大，故B错误。线速度v＝ ，由于半径减小，线速度减小，故C正确。周期T＝，角速度增大，则周期减小，故D正确。‎ ‎10. (2018·武汉华中师大附中模拟)如图所示，一根细线下端拴一个金属小球A，细线的上端固定在金属块B上，B放在带小孔的水平桌面上，小球A在某一水平面内做匀速圆周运动。现使小球A改到一个更低一些的水平面上做匀速圆周运动(图上未画出)，金属块B 在桌面上始终保持静止，则后一种情况与原来相比较，下面的判断中正确的是(　　)‎ A．金属块B受到桌面的静摩擦力变大 B．金属块B受到桌面的支持力变小 C．细线的张力变大 D．小球A运动的角速度减小 答案　D 解析　设A、B质量分别为m、M，A做匀速圆周运动的向心加速度为a，细线与竖直方向的夹角为θ，对B研究，B受到的摩擦力f＝Tsinθ，对A，有Tsinθ＝ma，Tcosθ＝mg，解得a＝gtanθ，θ变小，a减小，则静摩擦力变小，故A错误；以整体为研究对象知，B受到桌面的支持力大小不变，应等于(M＋m)g，故B错误；细线的拉力T＝，θ变小，T变小，故C错误；设细线长为l，则a＝gtanθ＝ω2lsinθ，ω＝ ，θ变小，ω变小，故D正确。‎ ‎11. (2018·晋江月考)如图所示，AB为竖直转轴，细绳AC和BC的结点C系一质量为m的小球，两绳能承受的最大拉力均为2mg。当细绳AC和BC均拉直时∠ABC＝90°，∠ACB＝53°，BC＝‎1 m。细绳AC和BC能绕竖直轴AB匀速转动，因而小球在水平面内做匀速圆周运动。当小球的线速度增大时，两绳均会被拉断，则最先被拉断的那根绳及另一根绳被拉断时的速度分别为(重力加速度g＝‎10 m/s2，sin53°＝0.8，cos53°＝0.6)(　　)‎ A．AC　‎5 m/s B．BC　‎5 m/s C．AC　‎5.24 m/s D．BC　‎5.24 m/s 答案　B 解析　当小球线速度增至BC被拉直后，由牛顿第二定律可得，竖直方向上：TAsin∠ACB＝mg　①，水平方向上：TAcos∠ACB＋TB＝m　②，由①式可得：TA＝mg，小球线速度增大时，TA不变，TB增大，当BC绳刚要被拉断时，TB＝2mg，由②可解得此时，v≈‎5.24 m/s；BC绳断后，随小球线速度增大，AC绳与竖直方向间夹角增大，设AC绳被拉断时与竖直方向的夹角为α，由TAC·cosα＝mg，TACsinα＝m，r′＝LAC·sinα，可解得，α＝60°，LAC＝ m，v′＝‎5 m/s，故B正确。‎ ‎12．(2018·衡水一模)某高速公路的一个出口路段如图所示，情景简化：轿车从出口A进入匝道，先匀减速直线通过下坡路段至B点(通过B点前后速率不变)，再匀速率通过水平圆弧路段至C点，最后从C点沿平直路段匀减速到D点停下。已知轿车在A点的速度v0＝‎72 km/h，AB长L1＝‎150 m；BC为四分之一水平圆弧段，限速(允许通过的最大速度)v＝‎36 km/h，轮胎与BC段路面间的动摩擦因数μ＝0.5，最大静摩擦力可认为等于滑动摩擦力，CD段为平直路段长L2＝‎50 m，重力加速度g取‎10 m/s2。‎ ‎(1)若轿车到达B点时速度刚好为v＝‎36 km/h，求轿车在AB下坡段加速度的大小；‎ ‎(2)为保证行车安全，车轮不打滑，求水平圆弧段BC半径R的最小值；‎ ‎(3)求轿车从A点到D点全程的最短时间。‎ 答案　(1)‎1 m/s2　(2)‎20 m　(3)23.14 s 解析　(1)v0＝‎72 km/h＝‎20 m/s，‎ AB长L1＝‎150 m，v＝‎36 km/h＝‎10 m/s，‎ 对AB段匀减速直线运动有v2－v＝－2aL1‎ 代入数据解得a＝‎1 m/s2。‎ ‎(2)汽车在BC段做匀速圆周运动，静摩擦力提供向心力，Ff＝m 为了确保安全，则须满足Ff≤μmg 联立解得：R≥‎20 m，即：Rmin＝‎20 m。‎ ‎(3)设AB段时间为t1，BC段时间为t2，CD段时间为t3，全程所用最短时间为t。‎ 由运动学规律得L1＝t1‎ πRmin＝vt2‎ L2＝t3‎ t＝t1＋t2＋t3‎ 联立以上各式，‎ 代入数据解得：t＝23.14 s。‎