2018届二轮复习　应用牛顿运动定律解决力学问题课件（共53张）（全国通用） 53页

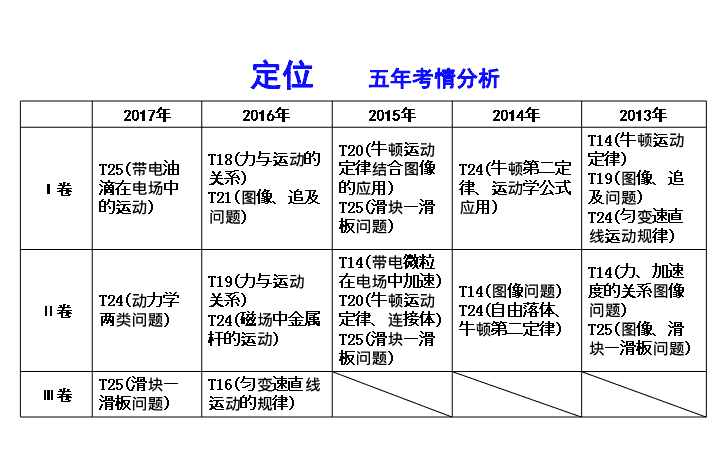
专题二　力与直线运动 定位 五年考情分析 2017 年 2016 年 2015 年 2014 年 2013 年 Ⅰ 卷 T25( 带电油滴在电场中的运动 ) T18( 力与运动的关系 ) T21( 图像、追及问题 ) T20( 牛顿运动定律结合图像的应用 ) T25( 滑块 — 滑板问题 ) T24( 牛顿第二定律、运动学公式应用 ) T14( 牛顿运动定律 ) T19( 图像、追及问题 ) T24( 匀变速直线运动规律 ) Ⅱ 卷 T24( 动力学两类问题 ) T19( 力与运动 关系 ) T24( 磁场中金属杆的运动 ) T14( 带电微粒在电场中加速 ) T20( 牛顿运动定律、连接体 ) T25( 滑块 — 滑板问题 ) T14( 图像问题 ) T24( 自由落体、牛顿第二定律 ) T14( 力、加速度的关系图像问题 ) T25( 图像、滑块 — 滑板问题 ) Ⅲ 卷 T25( 滑块 — 滑板问题 ) T16( 匀变速直线运动的规律 ) 专题 定位 本专题解决的是直线运动规律及其与牛顿运动定律的综合问题 . 高考对本专题的考查频率极高 , 与图像结合时以选择题为主 , 难度适中 ; 与牛顿运动定律综合时以计算题为主 , 难度中上 . 图像法、整体隔离法等是用到的主要思想方法 ; 连接体问题、两类动力学问题、传送带问题、滑块 — 滑板问题等是考查的重要问题 . 应考 建议 1. 熟练掌握运动学公式及适用条件 , 深刻理解各类图像的意义 . 2. 实际问题中做好过程分析及运动中的规律选取 . 3. 灵活运用牛顿运动定律和运动学规律处理综合问题 . 第 1 讲　应用牛顿运动定律解决力学问题 整 合 突 破 实 战 整合 网络要点重温 【 网络构建 】 【 要点重温 】 1. 匀变速直线运动的规律 (1) 速度公式 :v= . (2) 位移公式 :x= . (3) 速度和位移的关系式 : =2ax. (5) 任意相邻两个连续相等的时间 T 内的位移之差是一个恒量 , 即 Δx=x n+1 -x n = . v 0 +at aT 2 2.x-t,v-t,a-t 图像相关量间的关系 3. 整体法和隔离法的优点及使用条件 优点 条件 整体法 研究对象减少 , 忽略物体之间的相互作用力 , 方程数减少 , 求解简捷 连接体中各物体具有共同的加速度 , 用整体法 隔离法 易看清各个物体具体的受力情况 当系统内各物体的加速度不同时 , 求连接体内各物体间的相互作用力时 , 用隔离法 突破 热点考向聚焦 热点考向一　运动学基本规律的应用 【 核心提炼 】 1. 逆向思维法 : 匀减速直线运动可视为反方向的匀加速直线运动 . 2. 全程法 : 全过程中若加速度不变 , 虽然有往返运动 , 但可以全程列式 , 如类竖直上抛运动 , 此时要注意各矢量的方向 ( 即正负号 ). 3. 刹车类问题 : 先判断刹车时间 , 再进行分析计算 . 【 典例 1】 公路上的某个激光测速仪只能测定距离仪器 20 ～ 200 m 范围内汽车的车速 , 激光测速仪所在路段限速 54 km/h. 测速仪发出测速激光脉冲的时间极短 , 并能立即得到车速 , 且每隔 2 s 测速一次 . 一辆小轿车在距离测速仪 264 m 时司机就发现了前方的测速仪 , 并立即制动做匀减速运动 , 结果该小轿车驶入测速范围内后 , 第一次被测速激光脉冲照射到时恰好没有超速 , 且第二次测速时的速度为 50.4 km/h. 求 : (1) 小轿车做匀减速运动的加速度大小 ; (2) 小轿车在距离测速仪 264 m 时速度的最小值 . 〚审题突破〛 答案 : (1)0.5 m/s 2 　 (2)17 m/s 【 拓展延伸 】 在 “ 典例 1 ” 的情景中 , 小轿车驶入测速范围内后 , 最晚经过几秒才第一次被测速激光脉冲照射到 ? 小轿车在距离测速仪 264 m 时速度的最大值是多少 ? 答案 : 2 s 　 17.9 m/s 【预测练习1】 交管部门强行推出了 “ 电子眼 ” ,机动车擅自闯红灯的现象大幅度减少.现有甲、乙两汽车正沿同一平直马路同向匀速行驶,甲车在前,乙车在后,它们行驶的速度均为10 m/s.当两车快要到一十字路口时,甲车司机看到绿灯已转换成了黄灯,于是紧急刹车(反应时间忽略不计),乙车司机为了避免与甲车相撞也紧急刹车,但乙车司机反应较慢(反应时间为0.5 s).已知甲车紧急刹车时制动力为车重的0.4倍,乙车紧急刹车时制动力为车重的0.5倍,取g=10 m/s 2 ,求: (1)若甲车司机看到黄灯时车头距警戒线15 m.他采取上述措施能否避免闯 红灯? 答案 : (1) 能避免闯红灯　 答案 : (2)2.5 m (2) 为保证两车在紧急刹车过程中不相撞 , 甲、乙两车行驶过程中应保持多大距离 ? 热点考向二　挖掘图像信息解决动力学问题　　　　　　　 　　　　　　 　　　　　　 【核心提炼】 1. 从 v - t 图像巧分析四个运动量 (1) 速度 : 从速度轴上读出速度 , 正负表示物体的运动方向 . (2) 时间 : 从时间轴上读出时刻 , 两时刻的差值表示物体的运动时间 . (3) 位移 : 由图线与时间轴围成的面积表示位移 , 时间轴上方表示位移的方向与规定的正方向相同 , 下方表示位移的方向与规定的正方向相反 . (4) 加速度 : 由图线的斜率求得 , 斜率的正、负表示加速度的方向 . 2. 求解运动图像与牛顿第二定律综合问题的基本思路 【 典例 2】 如图 ( 甲 ) 所示 , 质量 m=2 kg 的物体在水平面上向右做直线运动 . 过 a 点时给物体作用一个水平向左的恒力 F 并开始计时 , 选水平向右为速度的正方向 , 通过速度传感器测出物体的瞬时速度 , 所得 v - t 图像如图 ( 乙 ) 所示 . 取重力加速度为 g=10 m/s 2 . 求 : 解析 : (1) 设物体向右做匀减速直线运动的加速度为 a 1 , 则由 v - t 图线得加速度大小 a 1 =2 m/s 2 , 方向水平向左 ; 设物体向左做匀加速直线运动的加速度为 a 2 , 则由 v - t 图线得加速度大小 a 2 =1 m/s 2 , 方向水平向左 . (1) 物体在 0 ～ 4 s 内和 4 ～ 10 s 内的加速度的大小和方向 ; 答案 : (1)2 m/s 2 , 水平向左　 1 m/s 2 , 水平向左 解析 : (2) 根据牛顿第二定律 , 有 F+μmg=ma 1 , F-μmg=ma 2 解得 F=3 N,μ=0.05. (2) 力 F 的大小和物体与水平面间的动摩擦因数 μ; (3)10 s 末物体离 a 点的距离和位置 . 答案 : (2)3 N 　 0.05 (3)2 m 　 a 点的左侧 【 预测练习 2】 ( 2017 · 广东佛山二模 ) 广州塔总高度达 600 m, 游客乘坐观光电梯大约一分钟就可以到达观光平台 . 若电梯的受力简化成只受重力与绳索拉力 , 已知电梯在 t=0 时由静止开始上升 ,a - t 图像如图所示 . 则下列相关说法正确的是 ( 　 　 ) A.t=4.5 s 时 , 电梯处于失重状态 B.5 ～ 55 s 时间内 , 绳索拉力最小 C.t=59.5 s 时 , 电梯处于超重状态 D.t=60 s 时 , 电梯速度恰好为零 D 解析: 由a - t图像可知,在0～5 s内电梯有向上的加速度,电梯处于超重状态,选项A错误;在0～5 s时间内,电梯处于超重状态,拉力大于重力;在5～55 s时间内,电梯处于匀速上升过程,拉力等于重力;在55～60 s时间内,电梯处于失重状态,拉力小于重力,选项B,C错误;因a - t图线与t轴所围的 “ 面积 ” 代表速度改变量,而图中横轴上方的 “ 面积 ” 与横轴下方的 “ 面积 ” 相等,则电梯的速度在t=60 s时为零,选项D正确. 热点考向三　应用牛顿运动定律解决 “ 传送带 ” 问题 【 核心提炼 】 1. 摩擦力的分析是突破点 物体与传送带达到 “ 共速 ” 的瞬间 , 是摩擦力发生 “ 突变 ” 的 “ 临界状态 ” ; 如果遇到匀变速运动的水平传送带 , 或者倾斜传送带 , 还要根据牛顿第二定律判断 “ 共速 ” 后的下一时刻是滑动摩擦力还是静摩擦力 . 2. “ 三步走 ” 分析传送带问题 【 典例 3】 如图所示 , 足够长的水平传送带 , 以初速度 v 0 =6 m/s 顺时针转动 . 现在传送带左侧轻轻放上质量 m=1 kg 的小滑块 , 与此同时 , 启动传送带制动装置 , 使得传送带以恒定加速度 a=4 m/s 2 减速直至停止 ; 已知滑块与传送带间的动摩擦因数 μ=0.2, 滑块可以看成质点 , 且不会影响传送带的运动 ,g=10 m/s 2 . 试求 : (1) 滑块与传送带共速时 , 滑块相对传送带的位移 ; 答案 : (1)3 m (2) 滑块在传送带上运动的总时间 t. 答案 : (2)2 s 【 预测练习 3】 ( 2017 · 贵州六校联考 ) 如图所示 , 传送带足够长 , 与水平面间的夹角 θ=37°, 并以 v=10 m/s 的速率逆时针匀速转动着 , 在传送带的 A 端轻轻地放一个质量为 m=1 kg 的小物体 , 若已知物体与传送带之间的动摩擦因数 μ=0.5, (g=10 m/s 2 ,sin 37°=0.6,cos 37°=0.8) 则下列有关说法正确的是 ( 　 　 ) A. 小物体运动 1 s 后 , 受到的摩擦力大小不适用公式 f=μF N B. 小物体运动 1 s 后加速度大小为 2 m/s 2 C. 在放上小物体的第 1 s 内 , 系统产生 50 J 的热量 D. 在放上小物体的第 1 s 内 , 至少给系统提供能量 70 J 才能维持传送带匀速 转动 B 热点考向四　应用牛顿运动定律解决 “ 滑块 — 滑板 ” 问题 【 核心提炼 】 1.从速度、位移、时间等角度,寻找滑块与滑板之间的联系. 2.滑块与滑板达到共速时,是摩擦力发生突变的临界条件. 3.滑块与滑板存在相对滑动的临界条件 (1)运动学条件:若两物体速度或加速度不等,则会相对滑动. (2)力学条件:一般情况下,假设两物体间无相对滑动,先用整体法算出一起运动的加速度,再用隔离法算出滑块 “ 所需要 ” 的摩擦力f,比较f与最大静摩擦力f m 的关系,若f>f m ,则发生相对滑动. 4.滑块不从滑板上掉下来的临界条件是滑块到达滑板末端时,两者共速. 【 典例 4】 ( 2017 · 全国 Ⅲ 卷 ,25 ) 如图 , 两个滑块 A 和 B 的质量分别为 m A =1 kg 和 m B =5 kg, 放在静止于水平地面上的木板的两端 , 两者与木板间的动摩擦因数均为 μ 1 =0.5; 木板的质量为 m=4 kg, 与地面间的动摩擦因数为 μ 2 =0.1. 某时刻 A,B 两滑块开始相向滑动 , 初速度大小均为 v 0 =3 m/s.A,B 相遇时 ,A 与木板恰好相对静止 . 设最大静摩擦力等于滑动摩擦力 , 取重力加速度大小 g=10 m/s 2 . 求 (1)B 与木板相对静止时 , 木板的速度 ; (2)A,B 开始运动时 , 两者之间的距离 . 〚 审题突破 〛 解析 : (1) 滑块 A 和 B 在木板上滑动时 , 木板也在地面上滑动 . 设 A,B 和木板所受的摩擦力大小分别为 f 1 ,f 2 和 f 3 ,A 和 B 相对于地面的加速度大小分别为 a A 和 a B , 木板相对于地面的加速度大小为 a 1 . 在物块 B 与木板达到共同速度前有 f 1 =μ 1 m A g,f 2 =μ 1 m B g,f 3 =μ 2 (m+m A +m B )g, 由牛顿第二定律得 f 1 =m A a A ,f 2 =m B a B , f 2 -f 1 -f 3 =ma 1 , 设在 t 1 时刻 ,B 与木板达到共同速度 , 其大小为 v 1 . 由运动学公式有 v 1 =v 0 -a B t 1 , v 1 =a 1 t 1 , 联立 , 代入已知数据得 v 1 =1 m/s. 答案 : (1)1 m/s 　 (2)1.9 m 【 预测练习 4】 ( 2017 · 吉林实验中学二模 ) 如图所示 , 在光滑的桌面上叠放着一质量为 m A =2.0 kg 的薄木板 A 和质量为 m B =3.0 kg 的金属块 B.A 的长度 L=2.0 m. B 上有轻线绕过定滑轮与质量为 m C =1.0 kg 的物块 C 相连 .B 与 A 之间的动摩擦因数 μ=0.10, 最大静摩擦力可视为等于滑动摩擦力 . 忽略滑轮质量及与轴、线之间的摩擦 . 起始时令各物体都处于静止状态 , 线被拉直 ,B 位于 A 的左端 ( 如图 ), 然后放手 , 求经过多长时间后 B 从 A 的右端脱离 ( 设 A 的右端距滑轮足够远 )( 取 g=10 m/s 2 )? 答案 : 4.0 s 实战 高考真题演练 1.[ 牛顿第二定律及运动学公式的应用 ]( 2016 · 全国 Ⅱ 卷 ,19 ) ( 多选 ) 两实心小球甲和乙由同一种材料制成 , 甲球质量大于乙球质量 . 两球在空气中由静止下落 , 假设它们运动时受到的阻力与球的半径成正比 , 与球的速率无关 . 若它们下落相同的距离 , 则 ( 　 　 ) A. 甲球用的时间比乙球长 B. 甲球末速度的大小大于乙球末速度的大小 C. 甲球加速度的大小小于乙球加速度的大小 D. 甲球克服阻力做的功大于乙球克服阻力做的功 BD 2.[ 运动学基本规律的应用 ]( 2016 · 全国 Ⅰ 卷 ,21 ) ( 多选 ) 甲、乙两车在平直公路上同向行驶 , 其 v - t 图像如图所示 . 已知两车在 t=3 s 时并排行驶 , 则 ( 　 　 ) A. 在 t=1 s 时 , 甲车在乙车后 B. 在 t=0 时 , 甲车在乙车前 7.5 m C. 两车另一次并排行驶的时刻是 t=2 s D. 甲、乙车两次并排行驶的位置之间沿公路方向的距离为 40 m BD 3.[ 挖掘图像信息解决动力学问题 ]( 2015 · 全国 Ⅰ 卷 ,20 ) ( 多选 ) 如图 (a), 一物块在 t=0 时刻滑上一固定斜面 , 其运动的 v - t 图线如图 (b) 所示 . 若重力加速度及图中的 v 0 ,v 1 ,t 1 均为已知量 , 则可求出 ( 　 　 ) 　　图 (a) 　　　　　　图 (b) 　　 A. 斜面的倾角 B. 物块的质量 C. 物块与斜面间的动摩擦因数 D. 物块沿斜面向上滑行的最大高度 ACD 4.[ 连接体问题 ]( 2015 · 全国 Ⅱ 卷 ,20 ) ( 多选 ) 在一东西向的水平直铁轨上 , 停放着一列已用挂钩连接好的车厢 . 当机车在东边拉着这列车厢以大小为 a 的加速度向东行驶时 , 连接某两相邻车厢的挂钩 P 和 Q 间的拉力大小为 F; 当机车在西边拉着车厢以大小为 a 的加速度向西行驶时 ,P 和 Q 间的拉力大小仍为 F. 不计车厢与铁轨间的摩擦 , 每节车厢质量相同 , 则这列车厢的节数可能为 ( 　 　 ) A.8 B.10 C.15 D.18 BC 5.[ 匀变速直线运动规律的应用 ]( 2014 · 全国Ⅰ卷,24 )公路上行驶的两汽车之间应保持一定的安全距离.当前车突然停止时,后车司机可以采取刹车措施,使汽车在安全距离内停下而不会与前车相碰.通常情况下,人的反应时间和汽车系统的反应时间之和为1 s,当汽车在晴天干燥沥青路面上以108 km/h的速度匀速行驶时,安全距离为120 m,设雨天时汽车轮胎与沥青路面间的动摩擦因数为晴天时的2/5,若要求安全距离仍为120 m,求汽车在雨天安全行驶的最大速度. 答案 : 20 m/s 6.[ 应用牛顿运动定律解决 “ 滑块 — 滑板 ” 问题 ]( 2015 · 全国 Ⅰ 卷 ,25 ) 一长木板置于粗糙水平地面上 , 木板左端放置一小物块 ; 在木板右方有一墙壁 , 木板右端与墙壁的距离为 4.5 m, 如图 (a) 所示 .t=0 时刻开始 , 小物块与木板一起以共同速度向右运动 , 直至 t=1 s 时木板与墙壁碰撞 ( 碰撞时间极短 ). 碰撞前后木板速度大小不变 , 方向相反 ; 运动过程中小物块始终未离开木板 . 已知碰撞后 1 s 时间内小物块的 v - t 图线如图 (b) 所示 . 木板的质量是小物块质量的 15 倍 , 重力加速度大小 g 取 10 m/s 2 . 求 : 　图 (a) 　　　　图 (b) (1) 木板与地面间的动摩擦因数 μ 1 及小物块与木板间的动摩擦因数 μ 2 ; 答案 : (1)0.1 　 0.4 (2) 木板的最小长度 ; 答案 : (2)6.0 m (3) 木板右端离墙壁的最终距离 . 答案 : (3)6.5 m 点击进入 提升 专题限时检测