高中物理竞赛复赛模拟试题一(有答案) 9页

复赛模拟试题一 1. 光子火箭从地球起程时初始静止质量（包括燃料）为 M0，向相距为 R=1.8×10 61.y. （光年） 的远方仙女座星飞行。要求火箭在 25 年（火箭时间）后到达目的地。引力影响不计。 1）、忽略火箭加速和减速所需时间，试问火箭的速度应为多大？ 2）、设到达目的地时火箭静 止质量为 M0ˊ，试问 M0/ M 0ˊ的最小值是多少？ 分析 ：光子火箭是一种设想的飞行器，它利用“燃料”物质向后辐射定向光束，使火箭获得 向前的动量。求解第 1 问，可先将火箭时间 a250 （年）变换成地球时间 ，然后由距离 R求出所需的火箭速度。火箭到达目的地时，比值 0 0 M M 是不定的，所谓最小比值是指火箭刚 好能到达目的地，亦即火箭的终速度为零，所需“燃料”量最少。利用上题（本章题 11）的 结果即可求解第 2 问。 解：1）火箭加速和减速所需时间可略，故火箭以恒定速度 飞越全程，走完全程所需火箭时 间（本征时间）为 a250 （年）。利用时间膨胀公式，相应的地球时间为 2 2 0 1 c 因 R 故 2 2 0 1 c R 解出 10 2 2 0 2 2 2 0 2 1096.011 1 c R cc R c c 可见，火箭几乎应以光速飞行。 （2）、火箭从静止开始加速至上述速度 ，火箭的静止质量从 M0 变为 M，然后作匀速运动， 火 箭质量不变。最后火箭作减速运动，比值 0 0 M M 最小时，到达目的地时的终速刚好为零，火箭 质量从 M变为最终质量 0M 。加速阶段的质量变化可应用上题（本章题 11）的（ 3）式求出。 因光子火箭喷射的是光子，以光速 c 离开火箭，即 u=c，于是有 2 1 0 1 1 M M （1） c 为加速阶段的终速度，也是减速阶段性的初速度。对减速阶段，可应用上题（本章题 11）的（4）式，式中的 m0 以减速阶段的初质量 M代入。又因减速时必须向前辐射光子， 故 u=-c ， 即有 2 1 0 1 1 M M （2） 由（ 1）、（2）式，得 10 2 0 2 2 2 0 2 2 0 104414 1 1 c R c R M M 2. 如图 52-1 所示，地面上的观察者认为在地面上同时发生的两个事件 A和 B，在相对地面以 速度 u （ u 平行于 x 轴，且与正方向同向）运动的火箭上的观察者的判断正确的是（ ） A、A 早于 B B 、B 早于 A C、A、B 同时发生 D 、无法判断 解：在地面（ S 系）上， ,AB xxx 0AB ttt ，在火箭（ S 系）中， 22 c uxtr c uxtrttt A A B BAB BA A AB xx c uxttr 2 BA A xx c ux 2 因 0r ， 0u ， 0BA xx ，故 0t 。即从火箭上观 察， B 事件在前， A 事件在后，选 B。 3. 如图 11-195 所示，正方形均质板重 G，用 4 根轻质杆铰链水平悬挂，外形构成边长为 a 的 立方体，现将方板绕铅垂对称轴旋转 θ角度，再用一细绳围绕四杆的中点捆住，使板平衡于 θ角位置。试求绳内的张力。 分析：初看此题，一般都会觉的比较复杂，因为题中铰链就有 8 个，加上 4 根轻质杆与绳子 有 4 个接触点，一共有 12 个受力点，而且初看甚至想象不出木板旋转 θ角度以后整个系统是 什么样子，即使把各个受力点的力逐个画出来也无济于事。应该先想一想哪些点都是对称的 （等价的） ，找出最基本的部分，再把空间方向确定下来，然后好画出各个力点的受力情况。 解：把木板绕铅垂对称轴旋转 θ角度以后，系统虽然不是一个很对称的立方体，但把系统绕 铅直轴旋转 90 度的整数倍，系统的与自身重合，说明四根轻杆的受力情况是完全一样的。系 统处于平衡状态，把四根轻杆，木板，绳组成的部分看成刚体，则刚体受四个铰接部分的力 而平衡，重力方向的平衡可以得出，竖直方向对每根轻杆的拉力 T 上 为： GT上4 （1） 而铰接处是否对轻杆有水平方向的作用力， 暂时还不好确定， 不过可以为 N// ，从俯 图来看四根轻杆的受力情况（如图 11-196 所示） ： 图中虚线表示正方形对角线的外延部分， 如果 N// 不在对角线方向上， 则四个 N// 对 O 点有一个力偶矩，将使得下面的部分旋转，与平衡假设相矛盾，因此水平弹力必然 在对角线方向，要么都向外，要么都向里（设向外为正，这种设法不会影响结果） 。 同样的道理，把木板隔离开来，可知木板对轻杆往下的拉力 下T 为： x y z O u A B 图 52-1 G 图 11-195 O //N 图 11-196 GT下4 （2） 而水平方向的作用力必沿对角线方向（否则木板旋转） ，木板对杆的作用力向里向外的性质与 上端铰链的方向相同，否则以绳对杆的作用点为支点，力矩无法平衡。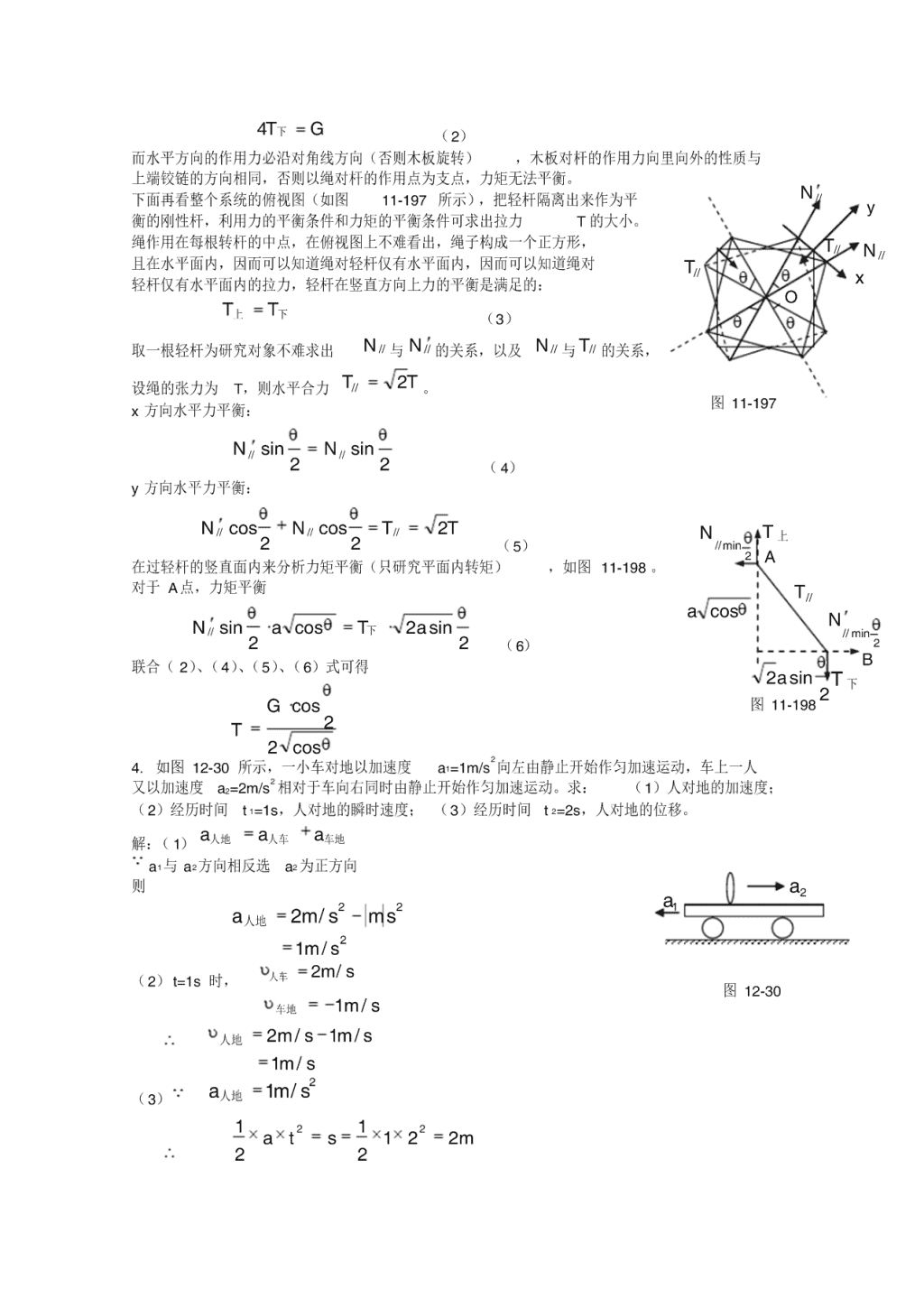 下面再看整个系统的俯视图（如图 11-197 所示） ，把轻杆隔离出来作为平 衡的刚性杆，利用力的平衡条件和力矩的平衡条件可求出拉力 T 的大小。 绳作用在每根转杆的中点，在俯视图上不难看出，绳子构成一个正方形， 且在水平面内，因而可以知道绳对轻杆仅有水平面内，因而可以知道绳对 轻杆仅有水平面内的拉力，轻杆在竖直方向上力的平衡是满足的： 下上 TT （3） 取一根轻杆为研究对象不难求出 //N 与 //N 的关系，以及 //N 与 //T 的关系， 设绳的张力为 T，则水平合力 TT 2// 。 x 方向水平力平衡： 2 sin 2 sin //// NN （ 4） y 方向水平力平衡： TTNN 2 2 cos 2 cos ////// （5） 在过轻杆的竖直面内来分析力矩平衡（只研究平面内转矩） ，如图 11-198 。 对于 A点，力矩平衡 2 sin2cos 2 sin// aTaN 下 （6） 联合（ 2）、（4）、（5）、（6）式可得 cos2 2 cosG T 4. 如图 12-30 所示，一小车对地以加速度 a1=1m/s2 向左由静止开始作匀加速运动，车上一人 又以加速度 a2=2m/s2 相对于车向右同时由静止开始作匀加速运动。求： （1）人对地的加速度； （2）经历时间 t 1=1s，人对地的瞬时速度； （3）经历时间 t 2=2s，人对地的位移。 解：（ 1） 车地人车人地 aaa a1 与 a2 方向相反选 a2 为正方向 则 22/2 smsma人地 2/1 sm （2） t=1s 时， 2 /m s人车 sm/1车地 smsm /1/2人地 sm/1 （3） 2/1 sma人地 msta 221 2 1 2 1 22 x y //N//T //T //N O 图 11-197 //T A B 下T 2 min// N 2 min// N 2 sin2a cosa 上T 图 11-198 1a 2a 图 12-30 5．有一小直径为 d 的试管，管内装有理想气体，其中有一段质量 m=2g的水银将理想气体和 空气隔开。当试管口向上时，气体在试管中的长为 L1（图 24-30 （ a）中的（ a）），当将管口向 下时，气体在试管中长为 L2（图 24-30 （b）中的（ b）），试求 L2/L 1 为多少？ 解： 如果是等温过程，可得理想气体的状态方程 常数PV 对于上述两种情况，可有 2211 VPVP 现在考虑在每一情况作用中在气体上的压强，如图 24-30 （b）所示，可得 S WP S WP P P V V 大气 大气 2 1 1 2 式中 S为试管内部的截面积， W为水银的重量， W=mg，则 S mgP S mgP SL SL V V 大气 大气 1 2 1 2 消去 S得 2 2 1 2 4 4 d mgP d mgP L L 大气 大气 6．有一个两端开口、粗细均匀的 U型玻璃细管，放置在竖直平面内，处在压强为 0p 的大气中， 两个竖直支管的高度均为 h，水平管的长度为 2h，玻璃细管的半径为 r,r?h ， 今将水平管内灌满密度为 ρ 的水银，如图 24-54 （a）所示。 1．如将 U型管两个竖直支管的开口分别封闭起来，使其管内空气压强均等于大气压强，问当 U型管向右作匀加速移动时，加速度应多大才能使水平管内水银柱长度稳定为 h 3 5 。 2．如将其中一个竖直支管的开口封闭起来，使其管内气体压强为 1atm，问当 U型管绕以另一 个竖直支管（开口的）为轴作匀速转动时，转数 n 应为多大才能使水平管内水银柱长度稳定 为 h 3 5 。 （U型管作以上运动时，均不考虑管内水银液面的倾斜） 解： 1、当 U型管向右加速移动时，水平管内的水银柱将向左边的竖直支管中移动，其稳定的 位置是留在水平管内的水银柱所受的水平方向的合力等于使其以恒定加速度 a 向右运动时所 需的力。由于竖直支管内空气在膨胀或压缩前后的温度相等，根据气态方程有 右管： hSphSp 10 3 4 左管： hSphSp 20 3 2 S 为管的截面积，图 24-54 （b）中， A、B 两处压强分别为： ghpp A 3 1 2 1ppB 1LP atP 2L atP P 图 24-30（b） h h2 图 24-54（a） A h 3 1 B a 图 24-54（b） 而留在水平管内的水银柱质量 hSm 3 5 其运动方程为 amSpp BA )( 由以上各式可得 )20/()49( 0 hghpa 2．当 U型管以开口的竖直支管为轴转动时，水平管内的水银柱将向封闭的竖直支管中移动， 其稳定位置是水平管内的水银柱所受的水平方向的合力，正好等于这段水银柱作匀速圆周运 动所需的向心力。由于封闭竖直支管内空气在压缩前后的温度相等，根据气态方程有 hShSp 3 2 0 S 为管的截面积。图 24-54 （c）中 A、B 两处的压强分别为 ghppA 3 1 0ppB 留在水平管内的水银柱的质量 hSm 3 5 其运动方程为 mRnRmSpp BA 222 4)( 其中 hR 6 7 由以上各式可得 2 1 22 0 )140/()69( hghpn 7. 有一块透明光学材料，由折射率略有不同的许多相互平行的，厚度 d=0.1mm 的薄层紧密连接构成，图 33-40 表示各薄层互相垂直的一个截面，若最下面一 层的折射率为 n0，从它往上数第 K层的折射率为 nK=n0-K v，其中 n0 =1.4,v=0.025 ， 今有一光线以入射角 i=60 °射向 O点，求此光线在这块材料内能达到的最大深 度？ 解：设光线进入材料后的折射角为 r ，则根据折射定律有 rni sinsin 0 ，此光线从最下面 一层进入向上数第一层时，入射角为 02 r ，折射角为 12 r ， 同样根据折射定律有 1100 2 sin 2 sin nn ， 也即 1100 coscos nn 光线从第一层进入第二层时，同样可得 1201 coscos nn 综合以上分析可得： KKnnnn coscoscoscos 221100 B A 3/h 图 24-54（c） r i O 0 1 2 1n 0n 2n 4n 3n 5n 图 33-40 因为 0025.00 KnnK ，所以 Kcos 随着 K 的增大而增大， K 则随着 K 的增大而减小， 即光线在顺序变化的介质中传播时将偏向折射率变大的方向。满足上式又当 Kcos 最接近 1 的 K 值即为光线能进入的最深薄层的序号，光线在这个薄层上将发生全反射，然后又逐层返 回下面最后射出透明材料。 因此求出能满足下式的 K的最大值 1coscoscos 0 0000 Kn n n n K K 因为 irnn sinsincos 000 代入上式得： 1sincos 0 Kn i K 解得： 76.21 025.0 866.041.1sin0 inK 取小于 21.76 的最大整数， 得 K=21，即在 n0 上面第 21 层下表面就是光线能到达的最深处， 所 以光线在这块透明材料内能达到的最大深度是 .2.21.0221 mmmmdKh 8. （1）图 33-98 所示为一凹球面镜，球心为 C，内盛透明液体，已知 C至液面 高度 CE为 40.0cm，主轴 CO上有一物 A，物离液面高度 AE恰好为 30.0cm 时， 物 A 的实像和物处于同一高度。 实验时光圈直径很小， 可以保证近轴光线成像。 试求该透明液体的折射率 n。 （2）体温计横截面如图 33-99 所示， 已知细水银柱 A 离圆柱面顶点 O的距离为 2R，R 为该圆柱面半径， C 为圆柱面中心轴位置。玻璃的折射率 n=3/2 ，E 代表人眼，求图示 横截面上人眼所见水银柱像的位置、虚实、正倒和放大倍数。 分析： （1）通过折射定律和光圈足够小的条件可求出液体的折射率。 （ 2）注意在近轴条件下 的近似，再通过几何知识即可求解。 解：（ 1）主轴上物 A 发出的光线 AB，经液体界面折射后沿 BD方向入射球面镜时，只要 BD延 长线过球心 C，光线经球面反射后必能沿原路折回。按光的可逆性原理，折回的光线相交于 A （图 33-100 ）。 对空气、液体界面用折射定律有 rni sinsin CBBE ABBE r in / / sin sin 当光圈足够小时， EB ，因此有 33.1 0.30 0.40 AE CEn (2) 先考虑主轴上点物 A发出的两条光线，其一沿主轴方向 ACOE入射界面，无偏折地出射， 进入人眼 E。其二沿 AP 方向以入射角 i 斜入射界面 P 点，折射角为 r。折射光线 PQ要能进入 人眼 E，P 点应非常靠近 O 点，或者入射角 i 和折射角 r 应很小。若角度以弧度量度，在小角 （近轴）近似下，折射定律 rin sinsin 可写为 nir 。这两条光线反向延长，在主轴上相 交于 A ， A 即为物 A之虚像点（图 33-101 ）。 对 AAP 用正弦定律，得 PA i PA i AA PAA sin)sin(sin 在小角（近轴）近似下： R2 OC E R 图 33-99 A C E O B D i r i 图 33-100 iiiniPAAPAA sin,sin OAPA 上式可写为 OA i ROA ini 2 解上式得 RR n ROA 4 2/32 2 2 2 为了分析成像倒立和放大情况，将水银柱看成有一定高度的垂轴小物体 AB，即然 AA ~ 是一 对共轭点，只要选从 B 发出的任一条光线经界面折射后，反向延长线与过 A 点垂轴线相交于 B ， B 是点物 B 虚像点，即 BA 是物 AB之正立虚像。 选从 B点发出过圆柱面轴心 C的光线 BC。该光线对界面来说 是正入射（入射角为零） ，故无偏折地出射，反向延长 BC线 交过 A 垂轴线于 B ，从 CBA ∽ΔABC得 放大率 33 R R AC CA AB BA 9．如图 41-83 所示，两个固定的均匀带电球面 A 和 B 分别带电 4Q和 Q（Q>0）。两球心之间的 距离 d 远大于两球的半径，两球心的连线 MN与两球面的相交处都开有足够小的孔，因小孔而 损失的电量可以忽略不计。 一带负电的质点静止地放置在 A 球左侧某处 P点， 且在 MN直线上。 设质点从 P点释放后刚好能穿越三个小孔，并 通过 B球的球心。试求质点开始时所在的 P 点 与 A 球球心的距离 x 应为多少？ 分析： 质点释放后，由于质点带负电， A 球和 B 球带正电，故质点先加速，穿过 A 球内时，不 受 A 球的电场力作用，但仍受 B 球的电场力， 进一步加速。在两球之间时，存在一质点所受 合力为零的点， 设此点为 S，且由于 A 球所带电 量大于 B 球带电量， S 点应离 B球较近。 所以质 点从 A球内出来后到 S 点这段距离内作减速运 动，从 S 点到 B球的第一个孔这段距离内作加 速运动。因此，为了使质点能到达 B 球的球心， 第一个必要条件是，质点必须通过 S点，即质点在 S 点的速度至少应大于零或至少等于零。 若质点能通过 S点，则如上述，从 S 点到 B球的第一个孔期间，质点沿 MN向右加速。由于质 点在 B球内不受 B 球的电场力作用，但仍受 A球向左的引力，质点减速，因此为了使用期质 点能通过 B球的球心，第二个必要条件是，质点在 B球球心处的速度应大于零或至少等于零。 本题的关键在于带电体系的电势能与带电质点的动能之和，在该质点运动过程中守恒。因此 质点刚好能通过 S 点的条件可表示为，质点在 P 点和 S点时，带电体系的电势能相等（注意， 质点在 P 点静止） 。同样，若质点在 S 点时带电体系的电势能大于（或等于）质点在 B 球球心 时带电体系的电势能，则表明质点若能通过 S点，就必定能通过（或刚好到达） B 球球心。 解： 根据分析，在 MN直线上在 A球和 B 球之间有一个 S 点，带电质点在 S 点受力为零。设 S 点与 A球和 B 球球心的距离为 1r 和 2r ，则 2 2 2 1 4 r Qk r Qk A B A B i C n P Q O E i nir 图 33-101 x d M N A B QQ4 P 图 41-83 drr 21 由以上两式，可解出 drdr 3 1; 3 2 21 带电质点从 P 点静止释放后，刚好能够到达 S点的条件是，它在 P点和 S 点的电势能相等， 即 21 44 r qQk r qQk dx qQk x qQk 式中 -q(q>0) 是带电质点的电量。把上面解出的 1r 和 2r 代入，得 dx 110 9 2 为了判断带电质点刚好到达 S 点后， 能否通过 B球球心， 需比较它在 S 点的电势能 SW 与它在 B 球球心处的电势能 BW 的大小，因 d Qqk r qQk r qQkWS 94 21 B B Rd kQq r qQk r qQkW 144 21 式中 BR 为 B 球的半径。由题设 BR ?d 故 dRd B 914 即 SB WW 因此，带电质点只要能到达 S 点，就必定能通过 B 球球心。于是，所求开始时 P 点与 A 球球 心的距离 x 即为上述结果，即 dx 110 9 2 10．如图 41-88 所示，在真空中有 4 个半径为 a 的不带电的相同导体球，球心分别位于边长 为 r （r?a）的正方形的四个顶点上。首先，让球 1 带电荷 Q（Q?0），然后取一细金属丝，其 一端固定于球 1 上，另一端分别依次与球 2、3、4、大地接触，每次接触时间都足以使它们达 到静电平衡。设分布在细金属丝上的电荷可忽略不计。试求流入大地的电量的表达式。 解：当球 1 与球 2 连接后， 用 1Q 和 Q2 分别表示球 1 和球 2 上的电量， 可得 2/12 QQQ 。球 1 与球 3 连接后，因球 1 和球 3 处于对称 位置，其电量 1Q 和 Q3 相等，故可得 .4/13 QQQ 球 1 与球 4 连 接后，电荷分布呈不对称状态，设连接后球 1 和球 4 上的电量分别 为 Q1 与 Q4。它们可利用等电势方法求出，即 图 41-88 B A a b d D l rkQrkQrkQakQU /2/// 43211 akQrkQrkQakQU //2// 43214 以上各式中， 计算各球上的电荷在另一球处引起的电势时， 利用了 r ?a 的条件。 由于 41 UU ， 且 ,4/141 QQQQ 故 8/2/1211 araQQ 8/2/1214 araQQ 利用 r ?a 的条件，略去二阶小量，上式可写成 8/2/1211 raQQ 8/2/1214 raQQ 最后将球 1 与球 4 断开并把球 1 接地。设接地后球 1 所带电量为 q1，电势为 1U ，则球 1 的电 势为 0/2// 43211 rkQrkQrkQakQU rQQQaq /2/ 4321 rraaQ /28/1224/18/5 raQ /24/18/5 此时球 1 上带负电，故流入大地的电量 入地Q 为 11 qQQ入地 raQraQ /24/18/58/2/121 8//2/21251 raQ 8//2/2341 raQ 答： . 2 234 1 8 r a Q 。