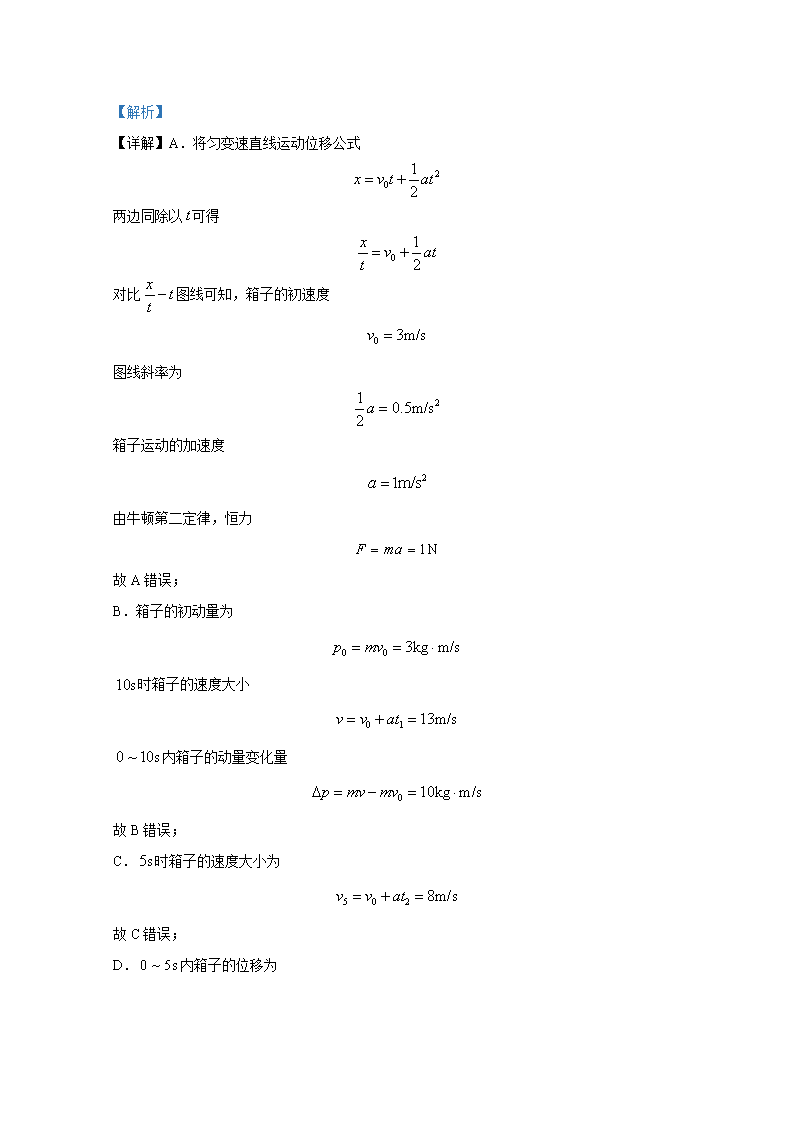山东省2020届高三物理高考实战模拟试题（三）（解析版） 25页

2020 届山东省高三新高考实战模拟物理试题（三） 一、单项选择题：本题共 8 小题。 1.在人类对微观世界进行探索的过程中，许多科学家作岀了不可磨灭的贡献，卢瑟福就是杰出 代表之一。关于卢瑟福在物理学上的成就，下列说法正确的是（ ） A.  粒子散射实验的重要发现是电荷的量子化，并且发现了中子 B. 卢瑟福用 粒子轰击氮核发现了质子，核反应方程为 4 14 17 1 2 7 8 1He N O H   C. 卢瑟福根据 粒子散射实验的结果，提出了原子核的结构模型 D. 卢瑟福根据 粒子散射实验的结果，发现原子核由质子和中子组成 【答案】B 【解析】 【详解】AC．卢瑟福根据 粒子散射实验的结果，提出了原子的核式结构模型，中子是查德 威克发现的，故 AC 错误； B．卢瑟福用 粒子轰击氮核，发现了质子，核反应方程为 4 14 17 1 2 7 8 1He N O H   ，故 B 正 确； D． 粒子散射实验不能说明原子核内存在中子和质子，故 D 错误。 故选 B。 2.一同学研究箱子的运动，让一质量为 1kgm  的箱子在水平恒力 F 的推动下沿光滑水平面做 直线运动，箱子运动的 x tt  图线如图所示，t 是从某时刻开始计时箱子运动的时间， x 为箱 子在时间t 内的位移，由此可知（ ） A. 箱子受到的恒力大小为 0.5NF  B. 0 ~10s 内箱子的动量变化量为5kg m/s C. 5s 时箱子的速度大小为5.5m/s D. 0 ~ 5s 内箱子的位移为 27.5m 【答案】D 【解析】 【详解】A．将匀变速直线运动位移公式 2 0 1 2x v t at  两边同除以t 可得 0 1 2 x v att   对比 x tt  图线可知，箱子的初速度 0 3m/sv  图线斜率为 21 0.5m/s2 a  箱子运动的加速度 21m/sa  由牛顿第二定律，恒力 1NF ma  故 A 错误； B．箱子的初动量为 0 0 3kg m/sp mv   10s 时箱子的速度大小 0 1 13m/sv v at   0 ~10s 内箱子的动量变化量 0 10kg m/sp mv mv     故 B 错误； C． 5s 时箱子的速度大小为 5 0 2 8m/sv v at   故 C 错误； D． 0 ~ 5s 内箱子的位移为 2 2 0 2 2 1 13 5m 1 5 m 27.5m2 2x v t at        故 D 正确。 故选 D。 3.石拱桥是中国传统的桥梁四大基本形式之一。假设某拱形桥为圆的一部分，半径为 R 。一辆 质量为 m 的汽车以速度 v 匀速通过该桥，图中Q 为拱形桥的最高点，圆弧 PQS 所对的圆心角 为90 ， ,P S 关于 QO 对称，汽车运动过程中所受阻力恒定，重力加速度为 g 。下列说法正 确的是（ ） A. 汽车运动到 P 点时对桥面的压力大于 cos45mg  B. 汽车运动到Q 点时牵引力大于阻力 C. 汽车运动到Q 点时，桥面对汽车的支持力等于汽车重力 D. 汽车从 P 点运动到 S 点过程中，其牵引力一定一直减小 【答案】D 【解析】 【详解】A．汽车运动到 P 点时，重力垂直于桥面的分力等于 cos45mg  ，由于汽车在竖直面 内做匀速圆周运动，沿半径方向有向心加速度，所以汽车对桥面的压力小于 cos45mg  ，故 A 错误； B．汽车在竖直面内做匀速圆周运动，运动到Q 点（圆弧最高点）时牵引力等于阻力，故 B 错误； C．由于汽车在竖直面内做匀速圆周运动，沿半径方向有向心加速度，所以汽车运动到Q 点时， 桥面对汽车的支持力小于汽车重力，故 C 错误； D．汽车从 P 点运动到Q 点过程中，重力沿圆弧切线方向的分力一直减小，设汽车与Q 之间 圆弧所对圆心角为 ，其牵引力 sinF mg f  一直减小，汽车从 Q 点运动到 S 点过程中，重力沿圆弧切线方向的分力一直增大，其牵引力 sinF f mg   一直减小，所以汽车从 P 点运动到 S 点过程中其牵引力一定一直减小，故 D 正确。 故选 D。 4.如图所示， 1 2O O 是半圆柱形玻璃体的对称面和纸面的交线， ,A B 是关于 1 2O O 对称且平行 的两束不同单色细光束，从玻璃体右方射出后的光路如图所示，MN 是垂直于 1 2O O 放置的光 屏， P 是屏上的一个光斑，根据该光路图，下列说法正确的是（ ） A. 在玻璃中， A 光的波长比 B 光的波长短 B. 在真空中， A 光的频率比 B 光的大 C. A 光的光子动量比 B 光的小 D. 通过同一双缝干涉装置， A 光的干涉条纹间距比 B 光的小 【答案】C 【解析】 【详解】AB．由光路图可知玻璃体对 B 光的折射率大于对 A 光的折射率，由此可知 B 光的频 率大于 A 光的频率，光的频率越小则波长就越长，故 A 光的波长比 B 光的波长长，故 AB 错 误； C．根据 hνp c  可知，光子的频率越大，则动量也就越大，故 A 光的光子动量比 B 光的小，故 C 正确； D．根据 lx d   可知，光的波长越长，则干涉条纹间距越大，即 A 光的干涉条纹间距比 B 光的大，故 D 错误。 故选 C。 5.北京时间 2019 年 5 月 17 日 23 时 48 分，我国成功发射第 45 颗北斗导航卫星。该卫星与此 前发射的倾斜地球同步轨道卫星（代号为 P ）、18 颗中圆地球轨道卫星（代号为Q ）和 1 颗地 球同步轨道卫星（代号为 S ）进行组网，为亚太地区提供更优质的服务。若这三种不同类型 卫星的轨道都是圆轨道，中圆地球轨道卫星的轨道半径是同步卫星的轨道半径的 2 3 ，下列说 法正确的是（ ） A. P 和 S 绕地球运动的向心加速度大小不相等 B. Q 和 S 绕地球运动的线速度大小之比为 6 : 2 C. Q 和 S 绕地球运动的周期之比为1: 2 D. P 和Q 绕地球运动的向心力大小一定相等 【答案】B 【解析】 【详解】A．由 2 MmG mar  可知， P 和 S 绕地球运动的向心加速度大小相等，故 A 错误； B．由 2 2 Mm vG mr r  可得 GMv r  又 2 3Q Sr r 则Q 和 S 绕地球运动的线速度大小之比为 : 6 : 2Q Sv v  故 B 正确； C．由 2 2 2MmG mrr T      可得 3 2π rT GM  Q 和 S 这两种不同类型轨道卫星绕地球运动的周期之比为 32: :1 2 6 : 93Q ST T      故 C 错误； D．由于 P 和Q 的质量不一定相等，所以 P 和Q 绕地球运动的向心力大小不一定相等，故 D 错误。 故选 B。 6.轻绳一端系在质量为 m 的物体 A 上，另一端系在一个套在粗糙竖直杆 MN 的圆环上。现用 水平力 F 拉住绳子上一点 O，使物体 A 从图中实线位置缓慢下降到虚线位置，但圆环仍保持 在原来位置不动。则在这一过程中，环对杆的摩擦力 F1 和环对杆的压力 F2 的变化情况是（ ） A. F1 保持不变，F2 逐渐增大 B. F1 逐渐增大，F2 保持不变 C. F1 逐渐减小，F2 保持不变 D. F1 保持不变，F2 逐渐减小 【答案】D 【解析】 【详解】以圆环、物体 A 及轻绳整体为研究对象，分析受力情况，如图 1 所示，根据平衡条 件得到，杆对环的摩擦力 f=G 保持不变； 杆对环的弹力 FN=F 再以结点 O 为研究对象，分析受力情况，如图 2 所示： 设绳与竖直方向夹角为θ，由平衡条件得到 F=mgtanθ 当物体 A 从图中实线位置缓慢下降到虚线位置过程中，θ逐渐减小，则 F 逐渐减小，FN 逐渐 减小。据牛顿第三定律可得，F1 保持不变，F2 逐渐减小。故 D 项正确，ABC 三项错误。 7.一质点静止在光滑水平面上，先向右做初速度为零的匀加速直线运动，加速度大小为 1a ，经 过时间t 后加速度变为零；又运动时间t 后，质点加速度方向变为向左，且大小为 2a ，再经过 时间t 后质点回到出发点。以出发时刻为计时零点，则在这一过程中（ ） A. 2 13a a B. 质点向右运动的最大位移为 2 2 8 5a t C. 质点回到出发点时的速度大小为 2 4 5 a t D. 最后一个时间 t 内，质点的位移大小和路程之比为 3∶5 【答案】C 【解析】 【详解】A．以向右为正方向，由速度公式有 1 1v a t 由题意知 1 2 30 x x x   由位移公式得 2 1 1 1 2x a t ， 2 1x v t ， 2 3 1 2 1 2x v t a t  解得 2 15a a 故 A 错误； B．根据题意，作出质点运动的 v t 图象，如图所示， 设向右从 1v 减速到 0 所用的时间为 t，则有 1 2v a t 又 1 1v a t 解得 1 5t t  根据 v t 图象的面积表示位移大小可知，质点向右运动的最大位移 2 1 1 1 1 1 1 1 8 2 2 5 5x v t v t v t a t     故 B 错误； C．质点回到出发点时所用的时间为 4 5t t t t    则对应的速度大小为 2 2 2 4 5v a t a t  故 C 正确； D．最后一个时间t 内，质点的位移大小为 2 1 2 1 3 2x x x a t    路程 2 1 1 1 1 1 1 4 1742 5 2 5 10s a t t a t t a t      所以最后一个时间t 内，质点的位移大小和路程之比为 15：17，故 D 错误。 故选 C。 8.位于水面上的波源 1 2,S S ，产生两列周期均为T 、振动方向相同、振幅均为 A 的相干波，实 线、虚线分别表示在同一时刻它们所发出的波的波峰和波谷，如图所示， a 、b 、c 、 d 、 e 是水面上的五个点，其中有一小树叶（未画出）位于 d 处，下列说法正确的是（ ） A. b 点的振动加强， c 点的振动减弱 B. 一段时间后，小树叶被水波推至b 处 C. a 、 e 两点在某时间内也会振动 D. 若波源 2S 突然停止振动，之后的 2T 内， b 点通过的路程为16A 【答案】D 【解析】 【详解】A．b 点是波峰和波峰叠加的点， c 点是波谷和波谷叠加的点，都是振动加强点，故 A 错误； B．机械波传播的过程中，各质点并不随波迁移，故小树叶只在原位置上下振动，故 B 错误； C． a 、 e 都是波峰和波谷叠加的点，属于振动减弱点，由于两波源振幅相同，故这两点均静 止不动，故 C 错误； D．若波源 2S 突然停止振动，由图像可知，在之后 2T 内，质点 b 仍是振动加强点，振幅为 2A ， 完成两次全振动，通过的路程为16A ，故 D 正确。 故选 D。 二、多项选择题：本题共 4 小题。 9.如图所示，在一个倾角为37 的长斜面底端O 点正上方 1.7mh  的 P 点处将一小球以速度 0v 水平抛出，恰好垂直击中斜面上的Q 点， sin37 0.6  。下列说法正确的是（ ） A. 小球的初速度 0 4m/sv  B. Q 点离O 点的距离| | 1.2mQO  C. 保持 h 不变，将小球以 02v 的速度水平抛出，则击中斜面的位置到O 点的距离小于 2 | |QO D. 若抛出点高度变为 2h ，欲使小球仍能垂直击中斜面，小球的初速度应调整为 02v 【答案】CD 【解析】 【详解】AB．如图甲所示 小球垂直击中斜面时，速度的偏向角为53 ，根据平抛运动规律的推论可知，速度偏向角的正 切值 tan53 2 2 tan37 h y h y yx        可得 9 0.9m17y h  1.2mx  | | 1.5msin53 xQO   小球在空中运动的时间 2( ) 0.4sh yt g   初速度 0 3m/sxv t   故 AB 错误； C．保持抛出点高度不变，初速度大小变为原来的两倍，如图乙所示 若无斜面，则小球应击中 O 点，实际击中点为轨迹与斜面的交点，显然离底端O 的距离小于 2 | |QO ，故 C 正确； D．若抛出点高度变为 2h ，根据小球垂直击中斜面的规律知 9 217y h   则小球下落的高度和水平位移均变为原来的两倍，根据 0 xv t  2ht g  联立解得 0 2 gv x h  故小球的初速度应调整为原来的 2 倍，故 D 正确。 故选 CD。 10.如图是利用太阳能驱动的小车，若小车在平直的水泥路上从静止开始加速行驶，经过时间 t 前进距离 s，速度达到最大值 vm，在这一过程中电动机的功率恒为 P，小车所受阻力恒为 f， 那么这段时间内( ) A. 小车做加速度逐渐减小的加速运动 B. 小车做匀加速运动 C. 电动机所做的功为 2 m 1 mv2 D. 电动机所做的功为 21 2 mfs mv 【答案】AD 【解析】 【详解】AB．小车电动机的功率恒定，速度不断变大，根据功率与速度关系公式 P=Fv 可知， 牵引力不断减小，根据牛顿第二定律， P/v−f=ma 故小车的运动是加速度不断减小的加速运动，故 A 正确，B 错误； CD．对小车启动过程，根据动能定理，有 W 电−fs= 21 2 mmv 这段时间内电动机所做的功为 W 电=fS+ 21 2 mmv 故 C 错误，D 正确． 故选 AD. 点睛：小车电动机的功率恒定，速度不断变大，牵引力不断减小，故小车的运动是加速度不 断减小的加速运动；结合动能定理列式求解电动机所做的功． 11.滑板运动是以滑行为特色、崇尚自由的一种运动，深受都市青年的喜爱。滑板的一种运动 情境可简化为如下模型：如图甲所示，将运动员（包括滑板）简化为质量 50kgm  的物块， 物块以某一初速度 0v 从倾角 37  的斜面底端冲上足够长的斜面，取斜面底端为重力势能零 势能面，该物块的机械能 E总 和重力势能 pE 随离开斜面底端的高度 h 的变化规律如图乙所示。 将物块视为质点，重力加速度 210m / s ，则由图中数据可得（ ） A. 初速度 0 5m / sv  B. 物块与斜面间的动摩擦因数为 0.3 C. 物块在斜面上运动的时间为 4 s3 D. 物块再次回到斜面底端时的动能为 375J 【答案】AD 【解析】 【详解】A．斜面底端为重力势能零势能面，则 2 01 1 625J2E mv 总 得 0 5m/sv  故 A 正确； B．当 pE E总 时，物块运动到最高点由图乙可知此时 m 1mh  根据功能关系，有 mcos 125Jsin hmg E     总 得物块与斜面间动摩擦因数 3 16   故 B 错误； CD．物块沿斜面上滑的时间 0 1 2 ssin cos 3 vt g g    上滑的位移 m 5 msin 3 hs   因为 tan  ，所以物块最终会沿斜面下滑，下滑的 2 2 2 15 sin cos 9 st g g    物块在斜面上运动的时间为 1 2 6 2 15 s9t t t   滑到斜面底端时的动能 m k 1 2 cos 375Jsin hE E mg     总 故 C 错误，D 正确。 故选 AD。 12.如图所示，足够长的光滑平行金属直导轨固定在水平面上，左侧轨道间距为 2d，右侧轨道 间距为 d。轨道处于竖直向下的磁感应强度大小为 B 的匀强磁场中。质量为 2m、有效电阻为 2R 的金属棒 a 静止在左侧轨道上，质量为 m、有效电阻为 R 的金属棒 b 静止在右侧轨道上。 现给金属棒 a 一水平向右的初速度 v0，经过一段时间两金属棒达到稳定状态。已知两金属棒运 动过程中始终相互平行且与导轨良好接触，导轨电阻忽略不计，金属棒 a 始终在左侧轨道上 运动,则下列说法正确的是（ ） A. 金属棒 b 稳定时的速度大小为 0 1 3 v B. 整个运动过程中通过金属棒 a 的电荷量为 02 3 mv Bd C. 整个运动过程中两金属棒扫过的面积差为 0 2 2Rmv B d D. 整个运动过程中金属棒 a 产生的焦耳热为 2 0 4 9 mv 【答案】BCD 【解析】 【详解】A．对金属棒 a、b 分别由动量定理可得 02 2 2BI d t mv mv     ， BI d t mv   联立解得 0mv mv mv  两金属棒最后匀速运动，回路中电流为 0，则 2B d v B d v     即 2v v  则 0 1 3v v ， 0 2 3v v  A 错误； B．在金属棒 b 加速运动的过程中，有 BI d t mv   即 0 2 3Bqd m v  解得 02 3 mvq Bd  B 正确； C．根据法拉第电磁感应定律可得 3 3 E B Sq I t tR R R        总 解得 0 2 2RmvS B d   C 正确； D．由能量守恒知，回路产生的焦耳热 2 2 2 2 0 0 1 1 1 22 22 2 2 3Q mv mv mv mv      则金属棒 a 产生的焦耳热 2 0 2 4 3 9Q Q mv   D 正确。 故选 BCD。 三、非选择题：本题共 6 小题。 13.用如图甲所示装置来探究功和物体速度变化的关系，木板上固定两个完全相同的遮光条 A B、 ，用不可伸长的细线将木板通过两个滑轮与弹簧测力计C 相连，木板放在安装有定滑轮 和光电门的轨道 D 上，轨道固定在水平桌面上，动滑轮上可挂钩码，滑轮质量、摩擦均不计。 （1）实验中轨道应倾斜一定角度，这样做的目的是__________； （2）用游标卡尺测量遮光条的宽度，如图乙所示，则遮光条的宽度 d  ______ cm； （3）主要实验步骤如下： ①测量木板（含遮光条）的质量 M ，测量两遮光条间的距离 L ，按图甲正确连接器材。 ②将木板左端与轨道左端对齐。由静止释放木板，木板在细线拉动下运动，记录弹簧测力计 示数 F 及遮光条 B A、 先后经过光电门所用的时间 2tt t、 ，则可以测出遮光条 B A、 通过光电门 时的速度大小和合外力对木板做的功； ③加挂钩码，重复②的操作，建立木板速度 v 和细线拉力对木板做的功W 的相关图像，分析 得出实验结论。 （4）根据实验中可能遇到的困难，回答下列问题： ①由静止释放木板的瞬间，弹簧测力计的示数会_______（填“变大”“变小”或“不变”）； ②如果将钩码的个数成倍增加，细线拉力对木板做的功W 将_______（填“会”或“不会”） 成倍增加； ③利用图像法处理实验结果时，应该建立_______（填“ v W  ”“ 2v W ”或 “ 2v W  ”）图像，如果得到的图像是线性变化的，则说明实验探究成功，此时图像的斜 率的表达式为 k  ________（用已知物理量的符号表示）。 【答案】 (1). 平衡摩擦力 (2). 0.560 (3). 变小 (4). 不会 (5). 2v W  (6). 2 M 【解析】 【详解】（1）[1]实验中轨道应倾斜一定角度，是利用木板的重力沿轨道向下的分力来平衡摩 擦力； （2）[2]根据游标卡尺的读数方法可得遮光条的宽度为 0.5cm 12 0.05mm 0.5cm 0.060cm 0.560cm     （4）[3]释放木板前，设弹簧测力计的示数为 1F ，根据受力平衡有 12F mg 释放的瞬间，对木板有 F Ma  对钩码有 12 2mg F m a   则有 1 2 mgF  1 2 2 F mgm M     故有 1F F  弹簧测力计的示数会变小 [4]由 1 2 2 F mgm M     可知，当钩码的个数成倍增加，即 m 加倍时， F 不是成倍增加的，而每次位移相等，故细线 拉力做的功不会成倍增加； [5][6]以木板为研究对象，根据动能定理有 2 2 21 1 1 2 2 2A BFL Mv Mv M v    故应该建立 2v W  图像，图像对应的函数关系为 2 2v WM    故 2k M  14.热敏电阻常用于温度控制或过热保护装置中。某种热敏电阻和金属热电阻的阻值 R 随温度 变化的关系如图甲所示。 （1）由图甲可知，在较低温度范围内，相对金属热电阻而言，该热敏电阻对温度变化的响应 更________（选填“敏感”或“不敏感”）。 （2）某同学利用上述热敏电阻制作了一个简易的温控装置，实验原理如图乙所示。现欲实现 衔铁在某温度时（此时热敏电阻的阻值为 0R ）被吸合，下列操作步骤正确的顺序是_______。 （填写各步骤前的序号） a.将热敏电阻接入电路 b.观察到继电器的衔铁被吸合 c.断开开关，将电阻箱从电路中移除 d.合上开关，调节滑动变阻器的阻值 e.断开开关，用电阻箱替换热敏电阻，将阻值调至 0R （3）若热敏电阻的阻值 tR 与温度t 的关系如下表所示， t /℃ 30.0 40.0 50.0 60.0 70.0 80.0 /tR  199.5 145.4 108.1 81.8 62.9 49.1 当通过继电器的电流超过 20mA 时，衔铁被吸合，加热器停止加热，实现温控。已知继电器 的电阻 20r   ，为使该裝置实现对 30 C ~80 C 之间任一温度的控制，电源 E 应选用 _______，滑动变阻器 xR 应选用_______。（填选项前的字母） A.电源 1E （3V ，内阻不计） B.电源 2E （ 6V ，内阻不计） C.滑动变阻器 1(0 ~ 200 )R  D.滑动变阻器 2 (0 ~ 500 )R  【答案】 (1). 敏感 (2). edbca (3). B (4). D 【解析】 【详解】（1）[1]图甲中横轴表示温度，纵轴表示电阻，随着温度的升高，金属热电阻的阻值 略微增大，而该热敏电阻的阻值明显减小，所以这种热敏电阻在较低温度范围内，相对金属 热电阻而言，该热敏电阻对温度变化的响应更敏感 （2）[2]要实现衔铁在某温度时（此时热敏电阻的阻值为 0R ）被吸合，而衔铁被吸合时的电 流是一定的，所以关键是找到此时滑动变阻器的阻值。实现方法是：断开开关，用电阻箱替 换热敏电阻，将阻值调至 0R ，合上开关，调节滑动变阻器的阻值，观察到继电器的衔铁被吸 合，则此时滑动变阻器连入电路的阻值就是衔铁在某温度（此时热敏电阻的阻值为 0R ）被吸 合时滑动变阻器应连入电路的阻值，找到之后，再用热敏电阻替换掉电阻箱即可，正确顺序 为 edbca； （3）[3]在 30 C 时，电源电动势的最小值 320 (199.5 20) 10 V 4.39VE      所以电源应选用 2E ，故选 B； [4]在 80 C 时，选用电源 2E ，滑动变阻器的最小阻值为 6V 49.1 20 230.920mA       所以滑动变阻器应选用 2 (0 ~ 500 )R  ，故选 D。 15.滑雪是人们喜爱的运动之一。如图甲所示，固定于安全坐垫上的小孩抱一玩具熊，从如图 乙所示雪道的 A 点沿倾角为 60 的雪道 AB 下滑，雪道 BC 面水平，滑到C 点时把玩具熊平抛 后小孩和玩具熊分别落在 D E、 两点。已知雪道上 A 、C 两点的高度差为 h ， B ，C 长度为 3 3 h ，安全坐垫与雪道间的动摩擦因数为 3 4 ， 2CD DE 。不计空气阻力和小孩经过 B 点 时的能量损失。重力加速度为 g 。求： （1）小孩滑至C 点时的速度大小； （2）抛出玩具熊后，小孩的水平速度与玩具熊的水平速度之比。 【答案】（1） gh ；（2） 2 3 【解析】 【详解】（1）由动能定理得 2 f 1 2mgh W mv  又 f 1cos60 sin 60 2BC hW mg mgx mgh      解得 v gh （2）由 2CD DE 可知，抛出玩具熊后小孩的水平位移与玩具熊的水平位移之比为 1 2: 2 : 3x x  由 tan 45y x  可得竖直位移之比为 1 2: 2 : 3y y  由平抛运动规律有 1 1 1x v t ， 2 2 2x v t 2 1 1 1 2y gt ， 2 2 2 1 2y gt 联立解得 1 2 2 3 v v  16.实验室内有一容积为 0V 的储气罐，里面充有压强为 06p 的空气（可视为理想气体），现用 该储气罐给原来气体压强为 0p 的篮球充气，使篮球内气体的压强达到 01.5p 。已知每个篮球 的体积为 0 1 4V 。不考虑温度变化及篮球体积的变化。 （1）求给两个篮球充气后，储气罐中气体的压强大小? （2）该储气罐最多能给几个这种篮球充足气？ 【答案】（1） 05.75p ；（2）36 【解析】 【详解】（1）设给两个篮球充气后储气罐中气体的压强大小为 p ，由于温度不变，则根据理 想气体状态方程有 0 0 0 0 0 0 0 1 16 2 2 1.54 4p V p V p V pV      解得 05.75p p （2）设该储气罐最多能给 n 个这种篮球充足气，温度不变根据理想气体状态方程有 0 0 0 0 0 0 0 0 1 16 1.5 1.54 4p V np V n p V p V      解得 36n  17.如图所示，用一块长 1 1.0mL  的木板在墙和桌面间架设斜面，桌子高 0.8mh  ，长 2 1.5mL  。斜面与水平桌面间的倾角 53  。一个质量为 0.3kgBm  的小滑块 B 放在桌面 最右端，现将质量为 0.2kgAm  的小滑块 A 从斜面顶端由静止释放，滑块与斜面间的动摩擦 因数 1 0.5  ，滑块与水平桌面间的动摩擦因数 2 1 3  ，忽略滑块在斜面与桌面交接处的能 量损失，滑块 A 与滑块 B 发生正碰，碰后滑块 A 最终停在离桌面右端 2.4cm 处。滑块与木板 及桌面间的最大静摩擦力等于滑动摩擦力，A、B 均可视为质点，重力加速度 210m/sg  ， sin53 0.8  ， cos53 0.6  。求： （1）与 B 相碰前瞬间小滑块 A 的速度大小； （2）小滑块 B 的落地点距桌面最右端的水平距离。 【答案】（1）2m/s；（2）0.64m 【解析】 【详解】（1）在斜面上，对 A 分析，根据牛顿第二定律有 1 1sin cosA A Am a m g m g    又 2 1 1 1 1 2L a t 则滑块在斜面底端的速度 1 1 1 10m / sv a t  在水平桌面上，对 A 分析，斜面底部到滑块的距离 1 2 1 cos 0.9ms L L    设碰前瞬间 A 的速度为 2v ，根据动能定理有 2 2 2 1 2 1 1 1 2 2A A Am v m v m gs   得 2 2m/sv  （2）设碰撞后 A 返回的距离为 2s ，以水平向右为正方向 2 2 2.4 10 ms   ，根据动量守恒定 律有 3A A B B Am v m v m v  根据动能定理有 2 2 2 10 2 A A Am v m gs   碰后 B 做平抛运动，则有 21 2h gt ， Bx v t 联立解得滑块 B 的落地点距桌面右端的水平距离为 0.64mx  18.如图所示，在矩形区域 ABCD 内存在竖直向上的匀强电场，在 BC 右侧Ⅰ、Ⅱ两区域存在 匀强磁场，L1、L2、L3 是磁场的边界（BC 与 L1 重合），宽度相同，方向如图所示，区域Ⅰ的 磁感强度大小为 B1．一电荷量为 q、质量为 m（重力不计）的带正电点电荷从 AD 边中点以初 速度 v0 沿水平向右方向进入电场，点电荷恰好从 B 点进入磁场，经区域Ⅰ后又恰好从与 B 点 同一水平高度处进入区域Ⅱ．已知 AB 长度是 BC 长度的 3 倍． （1）求带电粒子到达 B 点时的速度大小； （2）求磁场的宽度 L； （3）要使点电荷在整个磁场中运动的时间最长，求区域Ⅱ的磁感应强度 B2 的最小值． 【答案】18. 02 3 3 v 19. 0 1 2 3 3 mv qB 20. B2≥1.5B1 【解析】 【分析】 粒子在匀强电场中做类平抛运动，将运动沿水平方向与竖直方向分解，根据动为学规律即可 求解；当粒子进入磁场时，做匀速圆周运动，由牛顿第二定律可确定运动的半径．最后由几 何关系可得出磁场的宽度 L；根据几何关系确定离开磁场的半径范围，再由半径公式可确定磁 感应强度． 【18 题详解】 设点电荷进入磁场时的速度大小为 v，与水平方向成θ角，由类平抛运动的速度方向与位移方 向的关系有：tanθ＝ 3 3 BC AB L L  则θ＝30° 根据速度关系有：v＝ 0 02 3 cos 3 v v   【19 题详解】 设点电荷在区域Ⅰ中的轨道半径为 r1，由牛顿第二定律得： 2 1 1 vqvB m r  ，轨迹如图： 由几何关系得：L＝r1 解得：L＝ 0 1 2 3 3 mv qB 【20 题详解】 当点电荷不从区域Ⅱ右边界离开磁场时，点电荷在磁场中运动的时间最长．设区域Ⅱ中最小 磁感应强度为 B，对应的轨迹半径为 r2，轨迹如图： 同理得： 2 2 vqvB m r  根据几何关系有：L＝r2(1＋sinθ) 解得：B＝1.5B1 【点睛】本题考查了粒子在电场与磁场中的运动，粒子在电场中做类平抛运动，在磁场中做 圆周运动，本题涉及了类平抛运动、匀速圆周运动，学会处理这两运动的规律：类平抛运动 强调运动的分解，匀速圆周运动强调几何关系确定半径与已知长度的关系．